6.4: La Red de Coincidencia L

Los ejemplos de las dos secciones anteriores sugieren el concepto básico detrás del emparejamiento sin pérdidas de dos niveles de resistencia diferentes usando una\(\text{L}\) red:

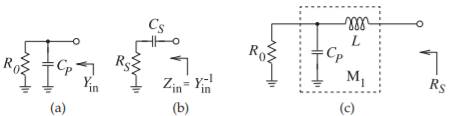
Figura\(\PageIndex{1}\): Transformación paralelo a serie: (a) resistencia con condensador de derivación; (b) su circuito en serie equivalente; y (c) el circuito transformador con inductor en serie agregado.

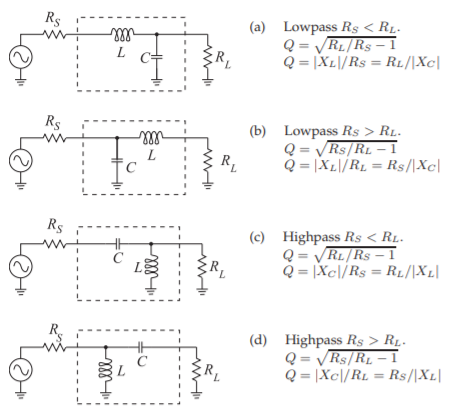
Figura\(\PageIndex{2}\): redes\(\text{L}\) coincidentes constituidas por un elemento reactivo en derivación y un elemento reactivo en serie. (\(R_{S}\)se corresponde con\(R_{L}\).) \(X_{C}\)es la reactancia del condensador\(C\), y\(X_{L}\) es la reactancia del inductor\(L\). Tenga en cuenta que con una red coincidente de dos elementos el ancho de banda\(Q\) y, por lo tanto, el ancho de banda

Paso 1: Utilice un elemento reactivo en serie (derivación) para transformar una resistencia más pequeña (mayor) hacia arriba (abajo) a un valor más grande (más pequeño) con una parte real igual al valor de resistencia deseado.

Paso 2: Utilice un elemento reactivo de derivación (serie) para resonar con (o cancelar) la parte imaginaria de la impedancia que resulta del Paso 1.

Por lo que una resistencia se puede transformar a cualquier valor resistivo mediante el uso de un circuito\(LC\) transformador.

Formalizando el enfoque de emparejamiento descrito anteriormente, tenga en cuenta que existen cuatro posibles redes\(\text{L}\) coincidentes de dos elementos (ver Figura\(\PageIndex{2}\)). Los dos posibles casos,\(R_{S} < R_{L}\) y\(R_{L} < R_{S}\), serán considerados en los siguientes subapartados.

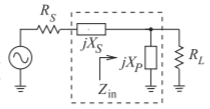
Figura\(\PageIndex{3}\): Topología de red coincidente de dos elementos para\(R_{S} < R_{L}\). \(X_{S}\)es la reactancia en serie y\(X_{P}\) es la reactancia paralela.

6.4.1 Ecuaciones de diseño para\(R_{S}<R_{L}\)

Considere la topología de red coincidente de la Figura\(\PageIndex{3}\). Aquí

\[\label{eq:1}Z_{\text{in}}=\frac{R_{L}(\jmath X_{P})}{R_{L}+\jmath X_{P}}=\frac{R_{L}X_{P}^{2}}{R_{L}^{2}+X_{P}^{2}}+\jmath\frac{X_{P}R_{L}^{2}}{R_{L}^{2}+X_{P}^{2}} \]

y el objetivo coincidente es\(Z_{\text{in}} = R_{S} − \jmath X_{S}\) que

\[\label{eq:2}R_{S}=\frac{R_{L}X_{P}^{2}}{R_{L}^{2}+X_{P}^{2}}\quad\text{and}\quad X_{S}=\frac{-X_{P}R_{L}^{2}}{X_{P}^{2}+R_{L}^{2}} \]

A partir de estos

\[\label{eq:3}\frac{R_{S}}{R_{L}}=\frac{1}{(R_{L}/X_{P})^{2}+1}\quad\text{and}\quad -\frac{X_{S}}{R_{S}}=\frac{R_{L}}{X_{P}} \]

Introduciendo las cantidades

\[\begin{align}\label{eq:4}Q_{S}&=\text{the }Q\text{ of the series leg }=|X_{S}/R_{S}| \\ \label{eq:5}Q_{P}&=\text{the }Q\text{ of the shunt leg }=|R_{L}/X_{P}| \end{align} \]

conduce a las ecuaciones finales de diseño para\(R_{S} < R_{L}\):

\[\label{eq:6}|Q_{S}|=|Q_{P}|=\sqrt{\frac{R_{L}}{R_{S}}-1} \]

El principio de red\(\text{L}\) coincidente es eso\(X_{P}\) y\(X_{S}\) será capacitiva o inductiva y tendrán el signo opuesto (es decir, la red\(\text{L}\) coincidente comprende un inductor y un condensador). También, una vez\(R_{S}\) y\(R_{L}\) se dan, se define el\(Q\) de la red y por lo tanto el ancho de banda; con la\(\text{L}\) red, el diseñador no tiene opción de circuito\(Q\).

Ejemplo\(\PageIndex{1}\): Matching Network Design

Diseñe un circuito para hacer coincidir una\(100\:\Omega\) fuente con una\(1700\:\Omega\) carga en\(900\text{ MHz}\). Supongamos que también se debe transferir una tensión de CC de la fuente a la carga.

Solución

Aquí\(R_{S} < R_{L}\), y así se puede utilizar la topología de la Figura\(\PageIndex{4}\) (a) y hay dos versiones, una con un inductor en serie y otra con un condensador en serie. Se elige la versión del inductor en serie\(\PageIndex{4}\) (ver Figura (b)) ya que permite aplicar polarización de CC. De Ecuaciones\(\eqref{eq:4}\) —\(\eqref{eq:6}\) las ecuaciones de diseño son

\[\label{eq:7}|Q_{S}|=|Q_{P}|=\sqrt{\frac{1700}{100}-1}=\sqrt{16}=4,\quad\frac{X_{S}}{R_{S}}=4,\quad\text{and}\quad X_{S}=4\cdot 100=400 \]

Esto indica que\(\omega L = 400\:\Omega\), y así el elemento serie es

\[\label{eq:8}L=\frac{400}{2\pi\cdot 9\cdot 10^{8}}=70.7\text{ nH} \]

Para el elemento de derivación junto a la carga,\(|R_{L}/X_{C}| = 4\), y así

\[\label{eq:9}|X_{C}|=\frac{R_{L}}{4}=\frac{1700}{4}=425 \]

Así\(1/\omega C = 425\) y

\[\label{eq:10}C=\frac{1}{2\pi\cdot 9\cdot 10^{8}\cdot 425}=0.416\text{ pF} \]

El diseño final de la red coincidente se muestra en la Figura\(\PageIndex{4}\) (c).

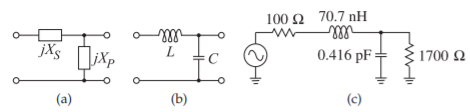
Figura\(\PageIndex{4}\): Desarrollo de redes coincidentes para Ejemplo\(\PageIndex{1}\).

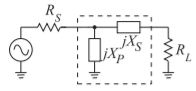
Figura\(\PageIndex{5}\): Topología de red coincidente de dos elementos para\(R_{S} > R_{L}\).

6.4.2 Diseño\(L\) de redes para\(R_{S}>R_{L}\)

Para\(R_{S} > R_{L}\), se utiliza la topología mostrada en\(\PageIndex{5}\) la Figura. Las ecuaciones de diseño para la\(L\) red\(R_{S} > R_{L}\) se derivan de manera similar y son

\[\label{eq:11}|Q_{S}|=|Q_{P}|=\sqrt{\frac{R_{S}}{R_{L}}-1} \]

\[\label{eq:12}-Q_{S}=Q_{P},\quad Q_{S}=\frac{X_{S}}{R_{L}},\quad\text{and}\quad Q_{P}=\frac{R_{S}}{X_{P}} \]

Ejemplo\(\PageIndex{2}\): Two-Element Matching Network

Diseñe una red pasiva de adaptación de dos elementos que logre la máxima transferencia de potencia desde una fuente con una impedancia de\(50\:\Omega\) hasta una carga con una impedancia de\(75\:\Omega\). Elija una red coincidente que no permita que DC pase.

Solución

\(R_{L} > R_{S}\), por lo que, a partir de la Figura\(\PageIndex{2}\), la topología de red correspondiente es

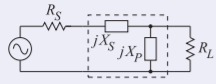
Figura\(\PageIndex{6}\)

Esta topología puede ser paso alto o paso bajo dependiendo de la elección de\(X_{S}\) y\(X_{P}\). El diseño procede encontrando las magnitudes de\(X_{S}\) y\(X_{P}\). En la coincidencia de dos elementos el circuito\(Q\) es fijo. Con\(R_{L} = 75\:\Omega\) y\(R_{S} = 50\:\Omega\).

El\(Q\) de la red coincidente es el mismo para los elementos en serie y paralelos:

\[|Q_{S}|=\frac{|X_{S}|}{R_{S}}=\sqrt{\frac{R_{L}}{R_{S}}-1}=0.7071\quad\text{and}\quad |Q_{P}|=\frac{R_{L}}{|X_{P}|}=|Q_{S}|=0.7071\nonumber \]

por lo tanto\(|X_{S}| = R_{S}\cdot |Q_{S}| = 50\cdot 0.7071 = 35.35\:\Omega\). También

\[|X_{P}|=R_{L}/|Q_{P}|=75/0.7071=106.1\:\Omega\nonumber \]

Ahora se pueden asignar tipos de elementos específicos a\(X_{S}\) y\(X_{P}\), y tenga en cuenta que deben ser de tipo opuesto.

La red de coincidencia de paso bajo es

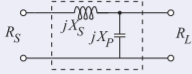
Figura\(\PageIndex{7}\)

\[X_{S}=+35.35\:\Omega,\quad X_{P}=-106.1\:\Omega\nonumber \]

La red de coincidencia de paso alto es

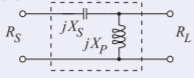
Figura\(\PageIndex{8}\)

\[X_{S}=-35.35\:\Omega,\quad X_{P}=+106.1\:\Omega\nonumber \]

Este diseño de paso alto satisface el criterio de diseño de que la CC no se pasa, ya que la CC está bloqueada por el condensador en serie.

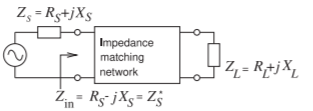
Figura\(\PageIndex{9}\): Una red coincidente que hace coincidir una carga compleja con una fuente con una impedancia Thevenin compleja.