3.7: Stripline
- Page ID
- 82322
En la Figura\(\PageIndex{1}\) (a) se muestra una línea de cinta simétrica. Una línea de cinta se asemeja a una línea de microcinta y comprende un patrón de conductor central simétricamente incrustado completamente dentro de un dieléctrico, cuyas capas superior e inferior son planos de tierra conductores. \(w\)Se considera que la tira de ancho tiene un espesor\(t\) que es muy pequeño de manera que la tira está a una\(h\) distancia de cada uno de los planos de tierra y los planos de tierra están separados por\(b = 2h\) D. La tira está completamente rodeada por el dieléctrico y por lo que este es un medio homogéneo y no hay necesidad de introducir una permitividad efectiva.
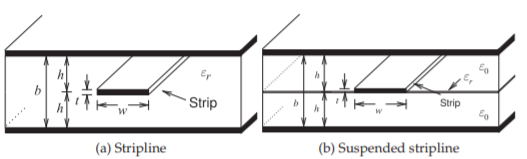
Figura\(\PageIndex{1}\): Líneas de transmisión Stripline. En la línea de cinta suspendida la tira está soportada por una membrana.
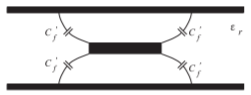
Figura\(\PageIndex{2}\): Capacitancia de flecos en las esquinas de la tira en líneas de transmisión de línea de cinta.
3.7.1 Impedancia característica de una línea de banda
Espesor Finito
La impedancia característica de una línea de cinta es [25, 26]
\[\label{eq:1}Z_{0}=\left[\frac{30\pi}{\sqrt{\varepsilon_{r}}}\right]\frac{(1-t/b)}{(w_{\text{eff}}/b)+C_{f}} \]
donde el ancho efectivo de la tira,\(w_{\text{eff}}\), se obtiene de
\[\label{eq:2}\frac{w_{\text{eff}}}{b}=\left\{\begin{array}{ll}{\frac{w}{b}-\left[\frac{(0.35-w/b)^{2}}{(1+12t/b)}\right]}&{\frac{w}{b}<0.35}\\{\frac{w}{b}}&{\frac{w}{b}\geq 0.35}\end{array}\right. \]
y
\[\label{eq:3}C_{f}=\frac{2}{\pi}\ln\left[\frac{1}{1-(t/b)}+1\right]-\frac{t}{\pi b}\ln\left\{\frac{1}{[1-(t/b)]^{2}}-1\right\} \]
\(C_{f}\)representa la capacitancia de flecos en los bordes de la tira e incorpora el efecto del grosor de la tira para\(t ≪ b\). La capacitancia de flecos por unidad de longitud (por ejemplo,\(\text{F/m}\)) en cada esquina de la tira es
\[\label{eq:4}C_{f}'=\frac{\epsilon_{0}\varepsilon_{r}C_{f}}{1-t/b} \]
y se muestra en la Figura\(\PageIndex{2}\). La precisión de estas fórmulas es mejor que\(1\%\) para\(W/(b − t) > 0.05\) y\(t/b < 0.025\).
Grosor Cero
Si la tira tiene espesor cero, la impedancia característica de la línea de cinta es
\[\label{eq:5}Z_{0}=\left[\frac{30\pi}{\sqrt{\varepsilon_{r}}}\right]\frac{1}{(w_{\text{eff}}/b)+2\ln 2/\pi}=\frac{94.25}{\sqrt{\varepsilon_{r}}}\frac{1}{(w_{\text{eff}}/b)+0.441} \]
donde el ancho efectivo de la tira,\(w_{\text{eff}}\), se obtiene de
\[\label{eq:6}\frac{w_{\text{eff}}}{b}=\left\{\begin{array}{ll}{\frac{w}{b}-\left(0.35-\frac{w}{b}\right)^{2}}&{\frac{w}{b}<0.35}\\{\frac{w}{b}}&{\frac{w}{b}\geq 0.35}\end{array}\right. \]
La capacitancia de flecos por unidad de longitud en cada esquina de la tira es
\[\label{eq:7}C_{f}'=\frac{\epsilon_{0}\varepsilon_{r}2\ln2}{\pi}=0.441\epsilon_{0}\varepsilon_{r} \]
Una línea de cinta soporta un modo puramente TEM y no hay dispersión dieléctrica debido a un cambio efectivo de permitividad con la frecuencia. Las pérdidas en una línea de cinta se deben a pérdidas dieléctricas, conductoras y radiativas. Las pérdidas radiativas se limitan a la energía perdida a la excitación del modo de guía de ondas de placa paralela, pero esto puede suprimirse cortocircuitando los planos de tierra juntos a intervalos regulares (digamos cada décima de una longitud de onda).
También se han desarrollado fórmulas para la impedancia característica de la línea de banda asimétrica, es decir, cuando la tira no está centrada entre los planos de tierra [27].
Una tira delgada de una línea de cinta simétrica tiene un ancho de\(0.5\text{ mm}\), está incrustada en un dieléctrico de permitividad relativa\(5.6\), y está entre planos de tierra separados por\(1\text{ mm}\). ¿Cuál es la impedancia característica de la línea de cinta?
Solución
La estructura se muestra en la Figura\(\PageIndex{1}\) (a) con\(w = 0.5\text{ mm}\) y\(b = 1\text{ mm}\). Ya que la tira es delgada, considérelo\(t = 0\). Entonces, de Ecuaciones\(\eqref{eq:2}\) y\(\eqref{eq:3}\)
\[\label{eq:8}\frac{w_{\text{eff}}}{b}=0.5\quad\text{and}\quad C_{f}=0.441 \]
y así
\[\label{eq:9}Z_{0}=\frac{94.25}{\sqrt{5.6}}\frac{1}{(0.5+0.441)}=42.77\:\Omega \]
3.7.2 Atenuación en una Línea de Banda
Para una línea de banda de baja pérdida con pérdida de radiación suprimida por vías entre los planos de tierra, la atenuación\(\alpha\),, comprende dos partes, la atenuación conductora,\(\alpha_{c}\), y la atenuación dieléctrica,\(\alpha_{d}\), de manera que\(\alpha=\alpha_{c}+\alpha_{d}\). De la ecuación (2.5.15)
\[\label{eq:10}\alpha_{c}=\frac{R}{2Z_{0}} \]
donde\(R\) está la resistencia por unidad de longitud de la línea. \(R\)es la suma de las resistencias de tira y tierra. A bajas frecuencias la resistencia de la banda es
\[\label{eq:11}R_{\text{strip}}=R_{s}/w \]
donde\(R_{s}\) esta la resistencia de la lamina de la tira y\(w\) es el ancho de la tira. El tratamiento para la resistencia al suelo es similar al descrito en la Sección 3.5.5 para microcinta. A bajas frecuencias de microondas
\[\label{eq:12}R_{\text{ground}}=\frac{1}{2}\frac{R_{sg}}{w}\frac{w/h}{w/h+5.8+0.03h/w},\quad\text{for }0.1\leq w/h\leq 10 \]
donde está la resistencia de la lámina del plano de tierra\(R_{sg}\). El factor de la mitad surge porque hay dos terrenos y la resistencia de cada uno es paralela. El efecto del suelo sobre la resistencia de la línea es pequeño. Ambos\(R_{\text{strip}}\) y\(R_{\text{ground}}\) aumentarán a frecuencias más altas a medida que las cargas se reordenen a frecuencias mucho más altas. Esto será considerado en el próximo capítulo.
La fórmula para la atenuación dieléctrica proviene de la Ecuación (3.5.26). La fórmula general para la constante de atenuación debida a la pérdida dieléctrica es, para una línea TEM de baja pérdida,
\[\label{eq:13}\alpha_{d}=\frac{\omega}{c}(\tan\delta)\frac{\varepsilon_{r}(\varepsilon_{e}-1)}{2\sqrt{\varepsilon_{e}}(\varepsilon_{r}-1)}\text{ Np/m} \]
Dado que la permitividad efectiva de una línea de cinta es solo la permitividad relativa del sustrato\(\varepsilon_{e} =\varepsilon_{r}\), entonces la ecuación se\(\eqref{eq:13}\) reduce a
\[\label{eq:14}\alpha_{d}=\frac{\omega}{2c}(\tan\delta)\sqrt{\varepsilon_{r}}\text{ Np/m}=\frac{1}{2}\omega\sqrt{\mu_{0}\varepsilon_{e}\varepsilon_{r}}(\tan\delta)\text{ Np/m} \]
(Tenga en cuenta que aquí\(\omega\) está la frecuencia de radián y no el ancho\(w\).)
La estructura de línea de cinta suspendida mostrada en la Figura\(\PageIndex{1}\) (b) tiene mínima pérdida dieléctrica y, por lo tanto, mínima dieléctrica. Los resonadores construidos con una línea de cinta suspendida tienen un alto\(Q\) y esta estructura se puede utilizar para realizar filtros de alto rendimiento.
Cuál es la atenuación de una línea de cinta simétrica en\(1\text{ GHz}\) con\(w = h = 0.5\text{ mm}\), una tira\(t = 4\:\mu\text{m}\) gruesa, metalización de plata y un sustrato FR-4. Los planos de tierra son\(4\:\mu\text{m}\) gruesos. Supongamos que los efectos de alta frecuencia en la resistencia de línea pueden ser ignorados
Solución
La tira es muy delgada y los resultados de Ejemplo se\(\PageIndex{1}\) pueden utilizar así\(Z_{0} = 42.77\:\Omega\). La resistividad de la plata es\(\rho_{\text{Ag}} = 14.87\text{ n}\Omega\cdot\text{m}\) y por lo tanto la resistividad laminar de la tira,\(R_{s} = \rho_{\text{Ag}}/t = (14.87\text{ n}\Omega\cdot\text{m})/(4\:\mu\text{m})=3.968\text{ m}\Omega\). De Ecuación\(\eqref{eq:11}\) la resistencia de la tira es\(R_{\text{strip}} = R_{s}/w = (3.968\text{ m}\Omega)/(1\text{ mm})=3.968\:\Omega\text{/m}\). La resistencia de la lámina de los terrenos es la misma que la de la tira así\(R_{sg} = 3.968\text{ m}\Omega\). De Ecuación\(\eqref{eq:12}\) la resistencia de los terrenos es
\[\begin{align} R_{\text{ground}}&=\frac{1}{2}\frac{R_{\text{sg}}}{w}\frac{w/h}{w/h+5.8+0.03h/w} \nonumber \\ \label{eq:15} &=\frac{1}{2}\frac{(3.968\text{ m}\Omega )}{(1\text{ mm})}\frac{1}{1+5.8+0.03}=\frac{3.968\:\Omega\text{/m}}{6.83}=0.581\:\Omega\text{/m}\end{align} \]
para que la resistencia total de la línea\(R = R_{\text{strip}} + R_{\text{ground}} = 4.549\:\Omega\text{/m}\). Por lo tanto, la atenuación debida a la pérdida del conductor es\(\alpha_{c} = R/(2Z_{0})=0.1064\text{ Np/m} = 0.924\text{ dB/m}\). FR-4 tiene una conductividad insignificante y la pérdida en el dieléctrico se debe a la relajación dieléctrica. FR-4 tiene una tangente de pérdida a\(1\text{ GHz}\) de\(0.01\) y una constante dieléctrica relativa de\(4.3\). De Ecuación\(\eqref{eq:14}\)
\[\label{eq:16}\alpha_{d}=\frac{1}{2}\omega\sqrt{\mu_{0}\varepsilon_{0}\varepsilon_{r}}(\tan\delta)\text{ Np/m}=0.2172\text{ Np/m}=1.886\text{ dB/m} \]
La atenuación total\(\alpha =\alpha_{c}+\alpha_{d} = (0.924 + 1.886)\text{ dB/m} = 2.810\text{ dB/m}\).
3.7.3 Fórmulas de diseño para una línea de banda
La síntesis de una línea de cinta simétrica con un sustrato que tiene una permitividad\(\varepsilon_{r}\) y espesor relativos\(b\) requiere la determinación del ancho de la tira para una impedancia característica particular [25]. El ancho\(w\) se obtiene de
\[\label{eq:17}\frac{w}{b}=\left\{\begin{array}{ll}{x}&{\text{for }Z_{0}\leq 120/\sqrt{\varepsilon_{r}}\:\Omega}\\{0.85-\sqrt{0.6-x}}&{\text{for }Z_{0}>120/\sqrt{\varepsilon_{r}}\:\Omega}\end{array}\right. \]
donde
\[\label{eq:18}x=\frac{30\pi}{\sqrt{\varepsilon_{r}}Z_{0}}-\frac{2\ln2}{\pi}=\frac{94.25}{\sqrt{\varepsilon_{r}}Z_{0}}-0.441 \]


