5.4: Modelo de Capacitancia de Baja Frecuencia de Líneas Acopladas

El modelo de baja frecuencia de un par de líneas acopladas sin pérdidas comprende solo capacitancias. Un par de líneas acopladas, como se muestra en la Figura\(\PageIndex{1}\) (a), tiene cuatro terminales. A frecuencias muy bajas\(V_{1}\) y\(V_{3}\) son idénticas como son los voltajes\(V_{2}\) y\(V_{4}\). Por lo que el modelo de baja frecuencia del par de líneas acopladas tiene apenas dos terminales además de tierra, como se muestra en la Figura\(\PageIndex{1}\) (b).

Las capacitancias en la Figura\(\PageIndex{1}\) (b) son la capacitancia de derivación\(C_{1}\)\(C_{2}\) y la capacitancia mutua\(C_{g}\). En el modo par, los voltajes en los terminales\(\mathsf{1}\) y\(\mathsf{2}\) son los mismos de manera que se\(C_{g}\) desvanece y el modelo de capacitancia de baja frecuencia del par de líneas acopladas en el modo par comprende solo las autocapacitancias\(C_{1}\) y\(C_{2}\) (ver Figura\(\PageIndex{1}\) (c)). En el modo impar, el voltaje en el terminal\(\mathsf{2}\) es el negativo del voltaje en el terminal\(\mathsf{1}\). El resultado es que hay una tierra virtual entre los terminales. Ahora un mejor modelo de circuito es el que se muestra en la Figura\(\PageIndex{1}\) (d). Aquí es donde se usa la restricción de que las líneas son de igual ancho. Esta suposición coloca el terreno virtual entre las capacitancias de igual valor. El caso simétrico es el de mayor interés. Si se van a analizar líneas acopladas asimétricas, el análisis se aparta en este punto y se requiere simulación EM.

Para proceder, el modelo de capacitancia se debe poner en forma de capacitancias por unidad de longitud y ponerlo en términos de los elementos de una matriz de capacitancia.

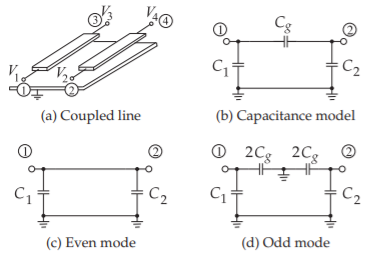
Figura\(\PageIndex{1}\): Modelos de muy baja frecuencia de un par de líneas acopladas.

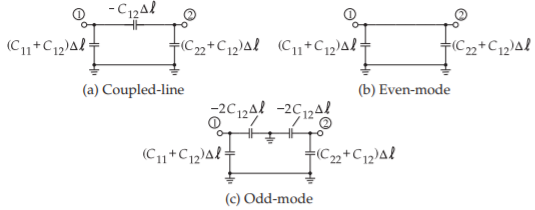
Figura\(\PageIndex{2}\): Modelos de capacitancia de baja frecuencia de un par de líneas acopladas de longitud\(\Delta\ell\).

La matriz de admitancia nodal indefinida del modelo de línea acoplada de baja frecuencia de la Figura\(\PageIndex{1}\) (b) es

\[\label{eq:1}\mathbf{Y}=\jmath\omega\left[\begin{array}{cc}{C_{1}+C_{g}}&{-C_{g}}\\{-C_{g}}&{C_{2}-C_{g}}\end{array}\right]=\jmath\omega\mathbf{C}\Delta\ell \]

donde\(\Delta\ell\) es la longitud de las líneas acopladas, y\(\mathbf{C}\) es la matriz de capacitancia por unidad de longitud (ver Ecuación (5.3.5)). Así, el modelo de capacitancia de baja frecuencia de un par de líneas acopladas de longitud\(\Delta\ell\) e igual anchura es como se muestra en la Figura\(\PageIndex{2}\) (a). Se encuentra en el análisis que\(C_{12}\) es negativo.

Para líneas acopladas simétricas (las tiras que tienen el mismo ancho) las capacitancias por unidad de longitud par e impar, tal como se definen en la definición de modos impar y par en la Sección 5.2, son

\[\label{eq:2}C_{e}=C_{11}+C_{12}\quad\text{and}\quad C_{o}=C_{11}-C_{12} \]

Es decir,

\[\label{eq:3}\mathbf{C}=\left[\begin{array}{cc}{C_{11}}&{C_{12}}\\{C_{12}}&{C_{22}}\end{array}\right]=\left[\begin{array}{cc}{\frac{1}{2}(C_{e}+C_{o})}&{\frac{1}{2}(C_{e}-C_{o})}\\{\frac{1}{2}(C_{e}-C_{o})}&{\frac{1}{2}(C_{e}+C_{o})}\end{array}\right] \]

5.4.1 Extracción de matriz de capacitancia

En esta sección se describe un procedimiento general para la extracción de la matriz de capacitancia de una serie de conductores acoplados [1]. Se pueden usar mediciones o simulaciones similares a mediciones. Esto se hace evaluando una capacitancia a la vez para diferentes conexiones de interconexiones entre sí.

Sin pérdida de generalidad, considere la estructura de tres líneas que se muestra en la Figura\(\PageIndex{3}\), donde hay cuatro conductores, incluyendo tierra. Se extrae una matriz de\(3\times 3\) capacitancia de las capacitancias de pares de conductores conectados. Hay siete combinaciones posibles, como se muestra en el lado izquierdo de la Figura\(\PageIndex{4}\). No obstante, debido a la reciprocidad\(C_{ij} = C_{ji}\), solo hay seis capacitancias\((C_{11},\: C_{12},\: C_{13},\: C_{22},\: C_{23},\) y\(C_{33})\) por determinar, y sólo se requieren seis conjuntos de conexiones. El séptimo set sirve como cheque. En una simulación EM, las conexiones se realizan convenientemente manteniendo el grupo negro a una tensión (por ejemplo,\(1\text{ V}\)) y el grupo blanco en\(0\text{ V}\). Las conexiones de capacitancia correspondientes se muestran a la derecha en la figura: las siete mediciones individuales de capacitancia son\(C_{A},\: C_{B},\: C_{C},\: C_{D},\: C_{E},\: C_{F},\) y\(C_{G}\). Así, los elementos de la matriz de capacitancia son

\[\label{eq:4}\left.\begin{array}{lll}{C_{11} = C_{11}' + C_{12}' + C_{13}'}&{}&{C_{12} = C_{21} = −C_{12}'}\\{C_{22} = C_{22}' + C_{12}' + C_{23}'}&{}&{C_{13} = C_{31} = −C_{13}'}\\{C_{33} = C_{33}' + C_{13}' + C_{23}'}&{}&{C_{23} = C_{32} = −C_{23}'}\end{array}\right\} \]

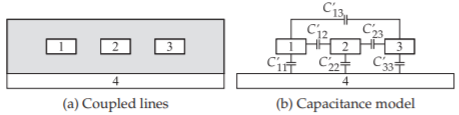
Figura\(\PageIndex{3}\): Estructura de tres líneas con cuatro conductores etiquetados\(\mathsf{1, 2, 3,}\) y\(\mathsf{4}\).

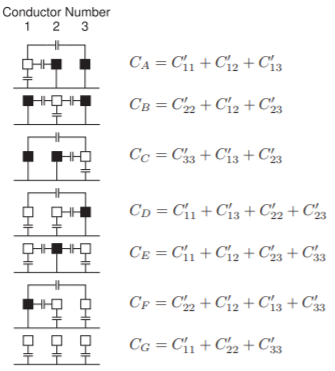
Figura\(\PageIndex{4}\): Combinaciones de conductores que conducen a diversas mediciones de capacitancia. Las capacitancias se\(C_{A},\ldots ,C_{G}\) miden entre el conductor identificado por el cuadrado abierto y la tierra que está conectada a los conductores, indicados por los cuadrados cerrados.

Usando las primeras seis mediciones de la Figura\(\PageIndex{4}\),

\[\label{eq:5}\left.\begin{array}{lll}{C_{A}=C_{11}}&{}&{C_{D} = C_{11} + 2C_{12} + C_{22}}\\{C_{B}=C_{22}}&{}&{C_{E} = C_{11} + 2C_{13} + C_{33}}\\{C_{C}=C_{33}}&{}&{C_{F} = C_{22} + 2C_{23} + C_{33}}\end{array}\right\} \]

Por lo tanto

\[\label{eq:6}\left.\begin{array}{lll}{C_{11}=C_{A}}&{}&{C_{12} = C_{21} =\frac{1}{2} (C_{D} − C_{A} − C_{B})}\\{C_{22}=C_{B}}&{}&{C_{13} = C_{31} =\frac{1}{2}(C_{E} − C_{A} − C_{C} )}\\{C_{33}=C_{C}}&{}&{C_{23} = C_{32} =\frac{1}{2}(C_{F} − C_{B} − C_{C})}\end{array}\right\} \]

Esta extracción no requiere que los anchos de las tiras sean los mismos.