5.9: Modelos de Líneas Acopladas Paralelas

5.9.1 Modelo Matriz de Cadena de Líneas Acopladas

La matriz de cadena de un par de líneas acopladas es la versión multipuerto de los\(ABCD\) parámetros de dos puertos y relaciona las corrientes de entrada y los voltajes en un extremo de un par de líneas acopladas con los voltajes y corrientes en el otro extremo. La matriz de cadena se deriva aquí siguiendo el desarrollo en [9]. Las características terminales de las líneas acopladas mostradas en la Figura 5.8.9 pueden expresarse en términos de los modos par e impar. Para el modo par

\[\label{eq:1}\left[\begin{array}{c}{\frac{1}{2}(V_{1}+V_{2})}\\{\frac{1}{2}(I_{1}+I_{2})}\end{array}\right] =\left[\begin{array}{cc}{\cos\theta_{e}}&{\jmath X_{0e}\sin\theta_{e}}\\{\jmath Y_{0e}\sin\theta_{e}}&{\cos\theta_{e}}\end{array}\right]\left[\begin{array}{c}{\frac{1}{2}(V_{3}+V_{4})}\\{\frac{1}{2}(I_{3}+I_{4})}\end{array}\right] \]

y para el modo impar

\[\label{eq:2}\left[\begin{array}{c}{\frac{1}{2}(V_{1}-V_{2})}\\{\frac{1}{2}(I_{1}-I_{2})}\end{array}\right] =\left[\begin{array}{cc}{\cos\theta_{o}}&{\jmath X_{0o}\sin\theta_{o}}\\{\jmath Y_{0o}\sin\theta_{o}}&{\cos\theta_{o}}\end{array}\right]\left[\begin{array}{c}{\frac{1}{2}(V_{3}-V_{4})}\\{-\frac{1}{2}(I_{3}-I_{4})}\end{array}\right] \]

donde\(Y_{0e} = 1/Z_{0e}\) es la admitancia característica de modo par y\(Y_{0o} = 1/Z_{0o}\) es la admitancia característica del modo impar. Además,\(\theta_{e}\) es la longitud eléctrica de las líneas para el modo par, y\(\theta_{o}\) es la longitud eléctrica de modo impar de las líneas. Agrupación de ecuaciones\(\eqref{eq:1}\) y\(\eqref{eq:2}\),

\[\label{eq:3}\left[\begin{array}{c}{V_{1}}\\{V_{2}}\\{I_{1}}\\{I_{2}}\end{array}\right] =\left[\begin{array}{cccc}{a_{11}}&{a_{12}}&{b_{11}}&{b_{12}}\\{a_{21}}&{a_{22}}&{b_{21}}&{b_{22}}\\{c_{11}}&{c_{12}}&{d_{11}}&{d_{12}}\\{c_{21}}&{c_{22}}&{d_{21}}&{d_{22}}\end{array}\right]\left[\begin{array}{c}{V_{3}}\\{V_{4}}\\{-I_{3}}\\{-I_{4}}\end{array}\right] \]

donde

\[\begin{align}\label{eq:4}a_{11}&=a_{22}=d_{11}=d_{11}=\frac{1}{2}(\cos\theta_{e}+\cos\theta_{o}) \\ \label{eq:5}a_{12}&=a_{21}=d_{12}=d_{21}=\frac{1}{2}(\cos\theta_{e}-\cos\theta_{o}) \\ \label{eq:6}b_{11}&=b_{22}=\jmath\frac{1}{2}(Z_{0e}\sin\theta_{e}+Z_{0o}\sin\theta_{o}) \\ \label{eq:7}b_{12}&=b_{21}=\jmath\frac{1}{2}(Z_{0e}\sin\theta_{e}-Z_{0o}\sin\theta_{o}) \\ \label{eq:8}c_{11}&=c_{22}=\jmath\frac{1}{2}(Y_{0e}\sin\theta_{e}+Y_{0o}\sin\theta_{o}) \\ \label{eq:9}c_{12}&=c_{21}=\jmath\frac{1}{2}(Y_{0e}\sin\theta_{e}-Y_{0o}\sin\theta_{0})\end{align} \]

De manera similar, la ecuación de admitancia para un par de líneas acopladas se deriva como

\[\label{eq:10}\left[\begin{array}{c}{V_{1}}\\{V_{2}}\\{V_{3}}\\{V_{4}}\end{array}\right] =\left[\begin{array}{cccc}{y_{11}}&{y_{12}}&{y_{13}}&{y_{14}} \\ {y_{21}}&{y_{22}}&{y_{23}}&{y_{24}} \\ {y_{31}}&{y_{32}}&{y_{33}}&{y_{34}} \\ {y_{41}}&{y_{42}}&{y_{43}}&{y_{44}}\end{array}\right]\left[\begin{array}{c}{I_{1}}\\{I_{2}}\\{I_{3}}\\{I_{4}}\end{array}\right] \]

donde

\[\begin{align} \label{eq:11} y_{11}&=y_{22}=y_{33}=y_{44}=-\jmath\frac{1}{2}(Y_{0e}\cot\theta_{e}+Y_{0o}\cot\theta_{o}) \\ \label{eq:12} y_{12}&=y_{21}=y_{34}=y_{43}=-\jmath\frac{1}{2}(Y_{0e}\cot\theta_{e}-Y_{0o}\cot\theta_{o}) \\ \label{eq:13} y_{13}&=y_{31}=y_{24}=y_{42}=\jmath\frac{1}{2}(Y_{0e}\csc\theta_{e}+Y_{0o}\csc\theta_{o}) \\ \label{eq:14} y_{14}&=y_{41}=y_{23}=y_{32}=\jmath\frac{1}{2}(Y_{0e}\csc\theta_{e}-Y_{0o}\csc\theta_{o})\end{align} \]

5.9.2\(ABCD\) Parámetros de Secciones de Línea Acoplada

La matriz de cadena de un par de líneas acopladas, Ecuación\(\eqref{eq:3}\), se puede utilizar para desarrollar los\(ABCD\) parámetros de redes de líneas acopladas de dos puertos [9]. Varias redes que se utilizan comúnmente en la realización de filtros y otros circuitos de microondas se muestran en la Tabla\(\PageIndex{1}\) con

\[\label{eq:15}\left[\begin{array}{c}{V_{1}}\\{I_{1}}\end{array}\right]=\left[\begin{array}{cc}{A}&{B}\\{C}&{D}\end{array}\right]\left[\begin{array}{c}{V_{2}}\\{-I_{2}}\end{array}\right] \]

Un enfoque para desarrollar la disposición física de los circuitos de microondas a partir del diseño eléctrico equipara los\(ABCD\) parámetros de las redes de línea acoplada a los\(ABCD\) del circuito de elementos agrupados sintetizado.

5.9.3 Síntesis de Conexiones Específicas de Línea Acoplada

La equivalencia de\(ABCD\) parámetros se puede utilizar en la síntesis de redes de microondas para transformar estructuras de líneas de transmisión desacopladas en un

a) Sección de línea acoplada interdigital de circuito abierto (redes de paso de banda/parada de banda) \[\begin{align}A&=D=(Z_{0e}\cot\theta_{e}+Z_{0o}\cot\theta_{o})/\Delta\nonumber \\ B&=\frac{\jmath}{2\Delta}[Z_{0e}^{2}+Z_{0o}^{2} \nonumber \\ &\quad −2Z_{0e}Z_{0o} (\cot\theta_{e}\cot\theta_{o} + \csc\theta_{e}\csc\theta_{o})]\nonumber \\ C&=2\jmath/\Delta\nonumber \\ \label{eq:16}\Delta&=Z_{0e}\csc\theta_{e} − Z_{0o}\csc\theta_{o}\end{align} \]	b) Sección de línea acoplada interdigital cortocircuitada (redes de paso de banda/parada de banda) \[\begin{align}A&=D=(Y_{0e}\cot\theta_{e}+ Y_{0o}\cot\theta_{o})/\Delta\nonumber \\ B&=2\jmath/\Delta\nonumber \\ C&=\frac{\jmath}{2\Delta}[Y_{0e}^{2}+Y_{0o}^{2}\nonumber \\ &\quad −2Y_{0e}Y_{0o} (\cot\theta_{e}\cot\theta_{o} + \csc\theta_{e}\csc\theta_{o})]\nonumber \\ \label{eq:17}\Delta&= Y_{0e}\csc\theta_{e} − Y_{0o}\csc\theta_{o}\end{align} \]
c) Sección de línea acoplada de meandro (redes de paso bajo) \[\begin{align}A&=D= (Z_{0e}\cot\theta_{e} − Z_{0o}\cot\theta_{o})/\Delta\nonumber \\ B&=2\jmath 2Z_{0e}Z_{0o} \cot\theta_{e}\tan\theta_{o}/\Delta\nonumber \\ C&=2\jmath/\Delta\nonumber \\ \label{eq:18}\Delta&=Z_{0e}\cot\theta_{e}+Z_{0o}\tan\theta_{o}\end{align} \]	d) Sección de líneas acopladas simétricas cortocircuitadas (redes de paso bajo) \[\begin{align}A&=D=(Y_{0e}\cot\theta_{e} + Y_{0o}\cot\theta_{o})/\Delta\nonumber \\ B&=2\jmath/\Delta\nonumber \\ C&=[\jmath /(2\Delta)] [Y_{0e}^{2} + Y_{0o}^{2}\nonumber \\ &\quad +2Y_{0e}Y_{0o} (\csc\theta_{e}\csc\theta_{o}− \cot\theta_{e}\cot\theta_{o})]\nonumber \\ \label{eq:19}\Delta &=Y_{0e}\csc\theta_{e} + Y_{0o}\csc\theta_{o}\end{align} \]
e) Sección de línea acoplada de combinación de circuito abierto (redes de paso de banda/parada de banda)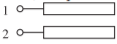 \[\begin{align}A&=D= (Z_{0e}\cot\theta_{e}+ Z_{0o}\cot\theta_{o})/\Delta\nonumber \\ B &= −\jmath 2Z_{0e}Z_{0o}\cot\theta_{e}\cot\theta_{o}/\Delta\nonumber \\ C&=2\jmath/\Delta\nonumber \\ \label{eq:20}\Delta&=Z_{0e}\cot\theta_{e} − Z_{0o}\cot\theta_{o}\end{align} \]	(f) Sección de línea acoplada de combinación cortocircuitada (redes de paso de banda/parada de banda) \[\begin{align}A&=D = (Y_{0o}\cot\theta_{o} + Y_{0e}\cot\theta_{e})/\Delta\nonumber \\ B&=2\jmath/\Delta\nonumber \\ C&= −\jmath 2Y_{0e}Y_{0o}\cot\theta_{e}\cot\theta_{o}/\Delta\nonumber \\ \label{eq:21}\Delta&=Y_{0o}\cot\theta_{o} − Y_{0e}\cot\theta_{e}\end{align} \]

Tabla\(\PageIndex{1}\):\(ABCD\) parámetros de secciones de líneas acopladas. Uso descrito en [10, 11, 12, 13].

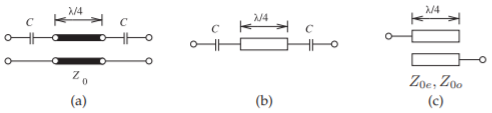
Figura\(\PageIndex{1}\): Equivalencia de línea acoplada: (a) una línea larga de un cuarto de longitud de onda con capacitancia en serie de entrada y salida; (b) diseño de microcinta; y (c) líneas acopladas equivalentes dispuestas en microcinta. La red en (a) es equivalente a la red en (c) si\(Z_{0e} = (1/C + 2Z_{0})\) y\(Z_{0o} = Z_{0}\).

sección de línea acoplada. Como ejemplo, considere la línea larga de un cuarto de longitud de onda acoplada capacitivamente mostrada en ambas Figuras\(\PageIndex{1}\) (a) y\(\PageIndex{1}\) (b). Esta configuración ocurre a menudo en el diseño del filtro y en la Figura\(\PageIndex{1}\) (c) se muestra una estructura equivalente que usa líneas acopladas y que no requiere condensadores discretos. La equivalencia se desarrolla equiparando los\(ABCD\) parámetros de los dos

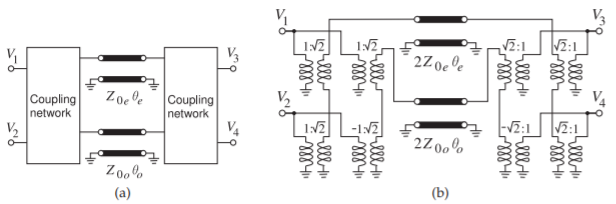
Figura\(\PageIndex{2}\): Modelos de un par de líneas acopladas usando líneas de modo par e impar: (a) con red de acoplamiento; y (b) con acoplamiento basado en transformador.

estructuras. La\(ABCD\) matriz de la red de líneas acopladas de la Figura\(\PageIndex{1}\) (c) se da en la Tabla\(\PageIndex{1}\) (a):

\[\begin{align} A&=\frac{Z_{0e}\cot\theta_{e} + Z_{0o}\cot\theta_{o}}{Z_{0e}\csc\theta_{e} − Z_{0o}\csc\theta_{o}}=D &C&=\frac{2\jmath}{Z_{0e}\csc\theta_{e} − Z_{0o}\csc\theta_{o}}\nonumber \\ \label{eq:22}B&=\frac{\jmath}{2}\frac{Z_{0e}^{2} + Z_{0o}^{2} − 2Z_{0e}Z_{0o} (\cot\theta_{e}\cot\theta_{o} + \csc\theta_{e}\csc\theta_{o})}{Z_{0e}\csc\theta_{e} − Z_{0o}\csc\theta_{o}}\end{align} \]

donde\(Z_{0e}\) y\(Z_{0o}\) son las impedancias modales,\(\theta_{e}\) y y\(\theta_{o}\) son las longitudes eléctricas de modo par e impar.

Desarrollar los\(ABCD\) parámetros de la línea larga de un cuarto de longitud de onda cargada capacitivamente en la Figura\(\PageIndex{1}\) (a) y equipararlos con los\(ABCD\) parámetros de la Ecuación\(\eqref{eq:22}\) conduce a una equivalencia entre la línea cargada (Figura\(\PageIndex{1}\) (b)) y la línea acoplada mostrada en la Figura \(\PageIndex{1}\)c), donde

\[\label{eq:23}Z_{0e}= (1/C + 2Z_{0})\quad\text{and}\quad Z_{0o} = Z_{0} \]

5.9.4 Modelo usando líneas de modo par e impar

El par de líneas acopladas en la Figura 5.8.9 se puede modelar usando líneas de transmisión de modo par e impar como se muestra en la Figura\(\PageIndex{2}\) (a). Si bien la partición de las tensiones y corrientes de los terminales de las líneas acopladas en componentes de modo par e impares es simple de describir matemáticamente (por ejemplo, la tensión en modo impares\(V_{o} =\frac{1}{2}(V_{1} − V_{2})\)), no hay una manera simple de representar la partición en forma de circuito. En cambio, en un simulador de circuito la red de acoplamiento de la Figura\(\PageIndex{2}\) (a) se modela usando fuentes de corriente controladas por voltaje [14]. En la Figura\(\PageIndex{2}\) (b) se muestra un modelo de circuito que es más conveniente de usar en el análisis de redes de líneas acopladas. La equivalencia de esta red a una línea acoplada se demuestra mostrando que los parámetros de matriz de cadena del circuito en la Figura\(\PageIndex{2}\) (b) son los mismos que los de Ecuaciones\(\eqref{eq:3}\) —\(\eqref{eq:9}\), ver Ejemplo\(\PageIndex{1}\).

Las líneas acopladas son un elemento importante en muchos circuitos de microondas, incluyendo filtros, redes coincidentes y redes de polarización. Muy a menudo el desarrollo del circuito conduce a una topología particular que se puede implementar usando redes de línea acoplada. Por ejemplo, la estructura en la parte superior de la Figura\(\PageIndex{3}\) (a) se conoce como sección interdigital de circuito abierto. El equivalente

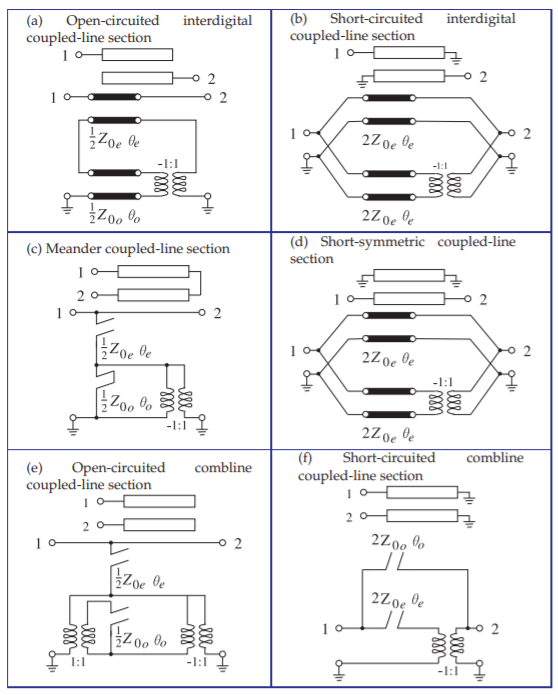
Figura\(\PageIndex{3}\): Secciones de líneas acopladas con modelos que comprenden líneas de transmisión individuales correspondientes a los modos par e impar.

de esta red, mostrado en la parte inferior de la Figura\(\PageIndex{3}\) (a), se deriva del circuito equivalente de línea acoplada que se muestra en la Figura\(\PageIndex{2}\) (b).

Ejemplo\(\PageIndex{1}\): Chain Matrix Parameters of Coupled Lines

Desarrollar la matriz de cadena del modelo de línea acoplada que se muestra en la Figura\(\PageIndex{2}\) (b) y mostrar que estos son los parámetros de matriz de cadena de una línea acoplada.

Solución

El modelo de línea acoplada se anota con voltajes y corrientes en la Figura\(\PageIndex{4}\). Usando la Tabla 2.A.1 de [15], las líneas de modo par e impar tienen los siguientes\(ABCD\) parámetros:

\[\begin{align}\label{eq:24}\left[\begin{array}{c}{V_{W}}\\{I_{W}}\end{array}\right]&=\left[\begin{array}{cc}{\cos\theta_{e}}&{\jmath 2Z_{e}\sin\theta_{e}}\\{\jmath\frac{1}{e}Y_{e}\sin\theta_{e}}&{\cos\theta_{e}}\end{array}\right]\left[\begin{array}{c}{V_{Y}}\\{I_{Y}}\end{array}\right] \\ \label{eq:25}\text{and}\quad\left[\begin{array}{c}{V_{X}}\\{I_{X}}\end{array}\right]&=\left[\begin{array}{cc}{\cos\theta_{o}}&{\jmath 2Z_{o}\sin\theta_{o}}\\{\jmath\frac{1}{2}Y_{o}\sin\theta_{o}}&{\cos\theta_{o}}\end{array}\right]\left[\begin{array}{c}{V_{Z}}\\{I_{Z}}\end{array}\right]\end{align} \]

Si bien se podrían usar los\(ABCD\) parámetros de los transformadores, es más conveniente anotar directamente las características de los terminales de los transformadores. Primero, los transformadores en el lado derecho se describen por

\[\begin{array}{cc}{V_{Y} = \frac{1}{\sqrt{2}}(V_{3} + V_{4})}&{I_{Y}=\frac{1}{2\sqrt{2}}[(-I_{3})+(-I_{4})]}\\ \label{eq:26}{}&{} \\ {V_{Z}=\frac{1}{\sqrt{2}}(V_{3}-V_{4})}&{I_{Z}=\frac{1}{2\sqrt{2}}[(-I_{3})-(-I_{4})]}\end{array} \]

Combinando ecuaciones\(\eqref{eq:24}\) —\(\eqref{eq:26}\) rendimientos

\[\label{eq:27}\left[\begin{array}{c}{V_{W}}\\{V_{X}}\\{I_{W}}\\{I_{X}}\end{array}\right]=\left[\begin{array}{cccc}{\sqrt{2}\cos\theta_{e}}&{\sqrt{2}\cos\theta_{e}}&{\jmath\sqrt{2}Z_{0e}\sin\theta_{e}}&{\jmath\sqrt{2}Z_{0e}\sin\theta_{e}}\\{\sqrt{2}\cos\theta_{o}}&{-\sqrt{2}\cos\theta_{o}}&{\jmath\sqrt{2}Z_{0o}\sin\theta_{o}}&{-\jmath\sqrt{2}Z_{0o}\sin\theta_{o}}\\{\jmath\frac{1}{2\sqrt{2}}Y_{0e}\sin\theta_{e}}&{\jmath\frac{1}{2\sqrt{2}}Y_{0e}\sin\theta_{e}}&{\frac{1}{2\sqrt{2}}\cos\theta_{e}}&{\frac{1}{2\sqrt{2}}\cos\theta_{e}}\\{\jmath\frac{1}{2\sqrt{2}}Y_{0o}\sin\theta_{o}}&{-\jmath\frac{1}{2\sqrt{2}}Y_{0o}\sin\theta_{o}}&{\frac{1}{2\sqrt{2}}\cos\theta_{o}}&{-\frac{1}{2\sqrt{2}}\cos\theta_{o}} \end{array}\right]\left[\begin{array}{c}{V_{3}}\\{V_{4}}\\{-I_{3}}\\{-I_{4}}\end{array}\right] \]

El desarrollo se completa utilizando las relaciones de voltaje y corriente determinadas por los transformadores en el lado izquierdo:

\[\begin{array}{cc}{V_{1}=\frac{1}{2\sqrt{2}}(V_{W}+V_{X})}&{I_{1}=\sqrt{2}(I_{W}+I_{X})}\\ \label{eq:28}{}&{}\\{V_{2}=\frac{1}{2\sqrt{2}}(V_{W}-V_{X})}&{I_{2}=\sqrt{2}(I_{W}-I_{X})}\end{array} \]

Combinando ecuaciones\(\eqref{eq:27}\) y\(\eqref{eq:28}\):

\[\label{eq:29}\left[\begin{array}{c}{V_{1}}\\{V_{2}}\\{I_{1}}\\{I_{2}}\end{array}\right]=\left[\begin{array}{cccc}{a_{11}'}&{a_{12}'}&{b_{11}'}&{b_{12}'}\\{a_{21}'}&{a_{22}'}&{b_{21}'}&{b_{22}'}\\{c_{11}'}&{c_{12}'}&{d_{11}'}&{d_{12}'}\\{c_{21}'}&{c_{22}'}&{d_{21}'}&{d_{22}'}\end{array}\right]\left[\begin{array}{c}{V_{3}}\\{V_{4}}\\{-I_{3}}\\{-I_{4}}\end{array}\right] \]

donde

\[\begin{aligned} a_{11}'&= a_{22}'= d_{11}' = d_{22}' = \frac{1}{2}(\cos\theta_{e} + \cos\theta_{o}) &a_{12}'&= a_{21}' = d_{12}' = d_{21}' =\frac{1}{2}(\cos\theta_{e} − \cos\theta_{o}) \\ b_{11}'&= b_{22}' =\jmath\frac{1}{2} (Z_{0e} \sin\theta_{e} + Z_{0o} \sin\theta_{o}) &b_{12}'&= b_{21}' = \jmath\frac{1}{2}(Z_{0e} \sin\theta_{e} − Z_{0o}\sin\theta_{o}) \\ c_{11}'&= c_{22}' = \jmath\frac{1}{2} (Y_{0e} \sin\theta_{e} + Y_{0o}\sin\theta_{c}) &c_{12}'&= c_{21}' =\jmath\frac{1}{2} (Y_{0e} \sin\theta_{e} − Y_{0o} \sin\theta_{o})\end{aligned}\nonumber \]

que es idéntica a la matriz de cadena de la línea de transmisión acoplada, Ecuación\(\eqref{eq:3}\). Así, la Figura\(\PageIndex{2}\) (b) es un modelo de circuito preciso de un par de líneas de transmisión acopladas.

5.9.5 Modelo alternativo de línea acoplada

En la sección anterior se desarrolló un modelo de un par de líneas acopladas y se mostró cómo el modelo se relacionaba con varias secciones de líneas acopladas. Si bien\(ABCD\) los parámetros se pueden usar para equiparar dos implementaciones diferentes, es útil tener una topología que pueda visualizarse y usarse para guiar la síntesis.

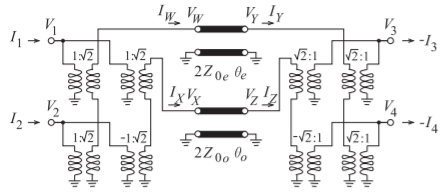
Figura\(\PageIndex{4}\): Modelo anotado de líneas acopladas utilizado en el Ejemplo 5.7.2.

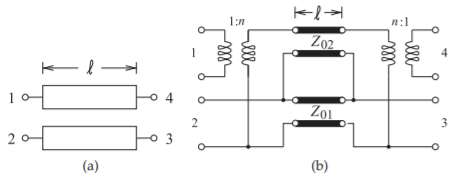
Figura\(\PageIndex{5}\): Un par de líneas acopladas simétricas: (a) disposición física; y (b) su modelo de circuito equivalente aproximado en una forma que aparece en la síntesis de red. \(n = (Z_{0e} + Z_{0o})/(Z_{0e} − Z_{0o})\).

La forma precisa del modelo de línea acoplada desarrollado en la sección anterior no suele ocurrir en la síntesis de redes. (En síntesis, como cuando se diseña un filtro usando líneas acopladas, una descripción matemática a veces se puede convertir en forma de circuito que incluye líneas de transmisión que están acopladas). En la Figura\(\PageIndex{5}\) (b) se muestra un modelo alternativo pero aproximado que tiene la misma topología que muchas redes sintetizadas.

Un par físico de líneas acopladas se muestra en la Figura\(\PageIndex{5}\) (a) con impedancia característica de modo par\(Z_{0e}\), e impedancia de modo impares\(Z_{0o}\), con el coeficiente de acoplamiento\(^{1}\)

\[\label{eq:30} K=\frac{Z_{0e}-Z_{0o}}{Z_{0e}+Z_{0o}} \]

El modelo de red equivalente aproximado correspondiente de la línea acoplada en la Figura\(\PageIndex{5}\) (a) fue desarrollado por Malherbe [16] y se muestra en la Figura\(\PageIndex{5}\) (b) con

\[\begin{align}\label{eq:31} Z_{01}&=\frac{Z_{0S}}{\sqrt{1-K^{2}}} \\ \label{eq:32} Z_{02}&=Z_{0S}\frac{\sqrt{1-K^{2}}}{K^{2}} \\ \label{eq:33}n&=\frac{1}{K}=\frac{Z_{0e}+Z_{0o}}{Z_{0e}-Z_{0o}} \\ \label{eq:34}Z_{0S}&=\sqrt{Z_{0e}Z_{0o}}\end{align} \]

La longitud eléctrica de las\(Z_{02}\) líneas\(Z_{01}\) y es la longitud eléctrica de la línea acoplada. La razón por la que este modelo es aproximado es que asume que las líneas acopladas son simétricas (por ejemplo, igual ancho para las líneas de microcinta) y utiliza un desarrollo basado en condensadores de baja frecuencia. También un par de líneas acopladas tiene dos longitudes eléctricas, la longitud eléctrica del modo par y la longitud eléctrica del modo impar. Entonces, lo mejor que se puede hacer es tomar las longitudes eléctricas de las\(Z_{02}\) líneas\(Z_{01}\) y como las longitudes eléctricas promedio de los modos par e impar. Sin embargo, este modelo se usa comúnmente en el desarrollo del diseño inicial de redes de línea acoplada que luego deben ser seguidas por el ajuste en un simulador de circuito de microondas.

5.9.6 Síntesis Aproximada a partir del Modelo de Línea Acoplada

El diseño eléctrico de redes de líneas acopladas conduce comúnmente a los parámetros del modelo de línea acoplada que se muestra en la Figura\(\PageIndex{5}\) (b). De estos se puede derivar el diseño físico. Es decir, dado\(n = 1/K,\: Z_{01},\) y\(Z_{02}\), los parámetros de línea acoplada\(Z_{0S},\: Z_{0e},\) y\(Z_{0o}\) se encuentran. Ecuaciones\(\eqref{eq:31}\) y\(\eqref{eq:32}\) conducen a dos ecuaciones para\(Z_{0S}\):

\[\begin{align}\label{eq:35}Z_{0S, (5.197)}&=Z_{01}\sqrt{1-K^{2}} \\ \label{eq:36}Z_{0S, (5.198)}&=Z_{02}\frac{K^{2}}{\sqrt{1-K^{2}}}\end{align} \]

Estos podrían ser diferentes y esto es resultado de que el modelo es aproximado. Si es así, entonces el rumbo correcto hacia adelante es usar la media geométrica:

\[\label{eq:37}Z_{0S}=\sqrt{Z_{0S, (5.197)}Z_{0S, (5.198)}} \]

Reordenando la ecuación\(\eqref{eq:33}\),

\[\begin{align}1+n&=1+\frac{Z_{0e}+Z_{0o}}{Z_{0e}-Z_{0o}}=\frac{Z_{0e}-Z_{0o}+Z_{0e}+Z_{0o}}{Z_{0e}-Z_{0o}}=\frac{2Z_{0e}}{Z_{0e}-Z_{0o}} \nonumber \\ \label{eq:38} 1-\frac{2}{n+1}&=\frac{n-1}{n+1}=1-\frac{Z_{0e}-Z_{0o}}{Z_{0e}}=\frac{Z_{0o}-Z_{0e}+Z_{0e}}{Z_{0e}}=\frac{Z_{0o}}{Z_{0e}}\end{align} \]

Es decir,

\[\label{eq:39}\frac{Z_{0e}}{Z_{0o}}=\frac{n+1}{n-1} \]

Combinando esto con la ecuación\(\eqref{eq:34}\),

\[\label{eq:40}Z_{0o}=Z_{0S}\sqrt{\frac{n-1}{n+1}}\quad\text{and}\quad Z_{0e}=\frac{Z_{0S}^{2}}{Z_{0o}} \]

Estas ecuaciones pueden ser utilizadas en la síntesis física. Por ejemplo, si\(Z_{0S}\) está cerca\(50\:\Omega\) y el sustrato es alúmina, entonces la relación se\(Z_{0e}/Z_{0o}\) puede utilizar para encontrar las dimensiones físicas a partir de la Tabla 5.8.3. De lo contrario, las fórmulas descritas en la Sección 5.6 se pueden usar iterativamente.

La longitud física de la línea acoplada se determina utilizando la media geométrica de las permitividades efectivas en modo par e impares para convertir a partir de la longitud eléctrica (en grados o longitudes de onda). A este diseño inicial le sigue el ajuste en un simulador de circuito de microondas.

Notas al pie

[1] Esta es la inversa del factor de acoplamiento,\(C\) utilizado anteriormente, ver Ecuación (5.145). Sin embargo, el uso\(C\) introduce confusión ya que los\(ABCD\) parámetros se utilizan a menudo en la síntesis de redes de línea acopl Tenga en cuenta que aquí\(K = 1/\) (factor de acoplamiento), es decir,\(K = 1/C\).