6.3: Guía de ondas de placa paralela
- Page ID
- 82319
Esta sección deriva los campos EM de propagación para la guía de ondas de placa paralela mostrada en la Figura\(\PageIndex{1}\). La guía de ondas de placa paralela mostrada en la Figura\(\PageIndex{1}\) (a) tiene planos conductores en la parte superior e inferior que (como aproximación) se extienden infinitamente en la\(x\) dirección. Los campos electromagnéticos introducidos entre las placas, digamos por un generador de voltaje sinusoidalmente variable a través de las placas, serán guiados por las cargas y corrientes inducidas en los conductores.
La estructura de guía de ondas de placa paralela se produce en muchos circuitos planos, como entre los planos de tierra y potencia de las placas de circuitos. Comprender la propagación EM soportada por guías de onda de placas paralelas permite tomar decisiones de diseño que suprimen los modos de propagación no deseados.
6.3.1 Modo TEM
En el modo EM transversal (TEM), todos los componentes\(E\) y de\(H\) campo están en el plano transversal a la dirección de propagación, es decir,\(E_{z} =0= H_{z}\). Así, la Ecuación (6.2.26) lo requiere\(E_{x},\: E_{y},\: H_{x},\) y\(H_{y}\) no puede variar con la posición en el plano transversal (es decir, con respecto a\(x\) y\(y\)). Así\(E_{x},\: E_{y},\: H_{x},\) y\(H_{y}\) debe ser constante entre las placas. Además, las condiciones límite requieren eso\(H_{y} = 0\) y\(E_{x} = 0\) en los conductores. Entonces en el modo TEM paralelo-placa, solo\(E_{y}\) y\(H_{x}\) existen, y son constantes. Ecuación
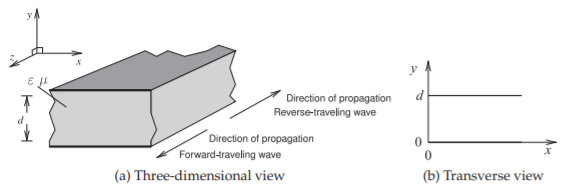
Figura\(\PageIndex{1}\): Guía de ondas de placa paralela.
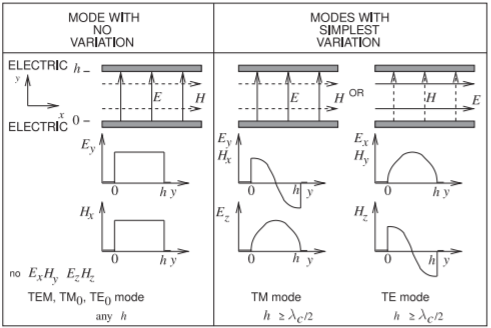
Figura\(\PageIndex{2}\): Modos de orden más bajo soportados por combinaciones de paredes eléctricas y magnéticas para el TEM\((=\text{TM}_{0} = \text{TE}_{0})\)\(\text{TM}_{1}\), y\(\text{TE}_{1}\) modos.
(6.2.25) lleva a
\[\label{eq:1}H_{x}=\frac{\gamma E_{y}}{\jmath\omega\mu}=\pm\frac{\jmath\omega\sqrt{\mu\varepsilon}}{\jmath\omega\mu}E_{y}=\pm\sqrt{\frac{\varepsilon}{\mu}}E_{y}=\pm\frac{1}{\eta}E_{y} \]
donde el signo más describe campos que viajan hacia adelante (propagándose en la\(+z\) dirección) y el signo menos describe campos que viajan hacia atrás (propagándose en la\(−z\) dirección). La cantidad\(\eta = \sqrt{\mu/\varepsilon}\) se llama impedancia de onda, es la impedancia intrínseca del medio entre las placas paralelas. Esta variación de campo se muestra a la izquierda en la Figura\(\PageIndex{2}\) (a). El modo TEM existe hasta DC.
Para determinar la impedancia característica de la guía de ondas de placa paralela primero calcule el voltaje de la placa superior con respecto a la placa inferior. Este voltaje es la integral del campo eléctrico entre las placas:
\[\label{eq:2}V=-\int_{y=0}^{d}E_{y}\text{e}^{-\gamma z}dy=E_{y}d\text{e}^{-\gamma z} \]
ya que\(E_{y}\) es una constante. La corriente en la placa superior en la\(z\) dirección se obtiene integrando la densidad de corriente superficial en la\(x\) dirección. Suponiendo que las placas tienen un ancho\(W\) en la\(x\) dirección entonces la corriente en la placa superior es
\[\label{eq:3}I=-\int_{x=0}^{W}J_{s}\cdot\hat{z}dx=H_{x}W\text{e}^{-\jmath z} \]
ya que\(E_{y}\) es una constante. En términos de voltaje y corriente (y por lo tanto tratando la guía de ondas de placa paralela como una línea de transmisión) la impedancia característica del modo TEM es
\[\label{eq:4}Z_{0}=\frac{V}{I}=\frac{E_{y}d}{H_{x}W}=\frac{\eta d}{W} \]
Aquí\(\eta\) está la impedancia intrínseca de un modo TEM en el medio. Como estamos considerando un modo TEM, la impedancia de onda del modo TEM es solo la impedancia intrínseca, es decir,
\[\label{eq:5}Z_{\text{TEM}}=E_{y}/H_{x}=Z_{0}|_{\text{free-space}}=\eta \]
\(\eta_{0} =\sqrt{\mu_{0}/\varepsilon_{0}}\)Al ser la impedancia de espacio libre, la impedancia característica se puede escribir
\[\label{eq:6}Z_{0}=\frac{\eta_{0}d}{W}\sqrt{\frac{\mu_{r}}{\varepsilon_{r}}}\quad\text{and}\quad Z_{\text{TEM}}=\eta=\eta_{0}\sqrt{\frac{\mu_{r}}{\varepsilon_{r}}} \]
La velocidad de fase\((= \omega/\beta)\) es solo la velocidad de la luz en el medio:
\[\label{eq:7}v_{p}=\frac{1}{\sqrt{\mu_{0}\varepsilon_{0}}}=\frac{c}{\sqrt{\mu_{r}\varepsilon_{r}}} \]
Las fórmulas para la atenuación se desarrollan en [1] y la atenuación del conductor
\[\label{eq:8}\alpha_{c}=\frac{R_{s}}{\eta d}\quad\text{(with SI units of Np/m)} \]
donde\(R_{s} = 1/(\sigma\delta_{s})\) está la resistencia superficial del conductor,\(\sigma\) es la conductividad del conductor, y\(\delta_{s}\) es la profundidad de la piel en el conductor. La atenuación debida a la pérdida dieléctrica es
\[\label{eq:9}\alpha_{d}=\frac{k^{2}\tan\delta}{2\beta}\quad\text{(with SI units of Np/m)} \]
6.3.2 Modo TM
El Modo Magnético Transversal (TM) se caracteriza por\(H_{z} = 0\). Otra restricción que se utilizará aquí en el desarrollo de las ecuaciones de campo es que no hay variación de los campos en la\(x\) dirección. Examinando la Ecuación (6.2.25) los únicos componentes del campo que podrían existir son\(E_{y},\: E_{z},\) y\(H_{x}\). En todas partes\(E_{y}\) es perpendicular, y\(H_{y}\) es paralelo, a las paredes eléctricas por lo que se satisfacen las condiciones de contorno para\(E_{y}\) y\(H_{x}\). \(E_{z}\)será paralelo a las paredes eléctricas en las paredes, por lo que las condiciones de límite deben aplicarse en la derivación\(E_{z}\).
Las condiciones de contorno son que el\(E\) campo paralelo a los muros conductores es cero. Considerando\(E_{z}\) solo, la Ecuación (6.2.18) se convierte en
\[\label{eq:10}\frac{d^{2}E_{z}}{dy^{2}}=-k_{c}^{2}E_{z} \]
La solución a la ecuación\(\eqref{eq:10}\) es
\[\label{eq:11}E_{z}=[E_{0}\sin(k_{c}y)+E_{1}\cos(k_{c}y)]\text{e}^{-\gamma z} \]
Para encontrar los coeficientes\(E_{0}\) y condiciones de\(E_{1}\) contorno se aplican de manera que\(E_{z}\) sea cero en\(y = 0\) y\(y = d\) (ya que el\(E\) campo paralelo a los conductores debe ser cero), es decir,
\[\label{eq:12}E_{z}|_{y=0}=0=E_{1}\quad\text{and}\quad E_{z}|_{y=d}=0=E_{0}\sin(k_{c}d) \]
Esto requiere eso\(\sin(k_{c}d)=0\), y por lo tanto requiere que existan valores discretos de\(k_{c}\):
\[\label{eq:13}k_{c}=m\pi/d\quad m=1,2,3,\ldots \]
(Tenga en cuenta que también\(m = 0\) es una solución pero requiere una derivación por separado, consulte el resumen de esta sección.) Cada valor de\(k_{c}\) identifica un modo diferente y\(m\) es el índice de modo. El modo\(m\) th es el\(\text{TM}_{m}\) modo e\(m\) indica el número de variaciones semi-sinusoidales de los campos en la\(y\) dirección. El\(\text{TM}_{m}\) modo se propaga si la longitud de onda de la señal es tal que\(\lambda ≥\lambda_{c}\), ¿dónde\(\lambda_{c}\) está la longitud de onda crítica del modo\(m\) th
Sustituyendo los resultados y supuestos anteriores (e.g.,\(\partial/\partial x = 0\)) en la Ecuación (6.2.25),
\[\begin{align}\label{eq:14}H_{z}&=0\: E_{x}=0\: H_{y}=0 \\ \label{eq:15}E_{z}&=E_{0}\sin(k_{c}y)\text{e}^{-\gamma z} \\ \label{eq:16}E_{y}&=-\frac{\gamma}{k_{c}^{2}}\frac{dE_{z}}{dy}=-\frac{\gamma}{k_{c}}E_{0}\cos(k_{c}y)\text{e}^{-\gamma z} \\ \label{eq:17}H_{x}&=\frac{\jmath\omega\varepsilon}{k_{c}^{2}}\frac{dE_{z}}{dy}=\frac{\jmath\omega\varepsilon}{k_{c}}E_{0}\cos(k_{c}y)\text{e}^{-\gamma z}\end{align} \]
Estas son las descripciones de campo completas de los modos de guía de ondas de placa paralela TM con variación cero en la\(x\) dirección. Recordemos que el número de onda\(k =\omega\sqrt{\mu\varepsilon}\).
Hay un número infinito de modos TM identificados por el índice\(m\), que determina el número de onda de corte,\(k_{c}\), del modo particular. La constante de propagación del modo\(m\) th, es decir, el\(\text{TM}_{m}\) modo, es
\[\label{eq:18}\gamma=\sqrt{k_{c}^{2}-k^{2}}=\sqrt{(m\pi/d)^{2}-\omega^{2}\mu\varepsilon} \]
La propagación solo es posible si\(\gamma\) tiene un componente imaginario. Así en un medio sin pérdidas\(\gamma = \jmath\beta\) y\(\beta =\sqrt{k^{2}-k_{c}^{2}}\). La frecuencia de corte por debajo de la cual no es posible la propagación es
\[\label{eq:19}f_{c}=\frac{1}{2\pi}\frac{k_{c}}{\sqrt{\mu\varepsilon}}=\frac{1}{2\pi}\frac{m\pi}{d\sqrt{\mu\varepsilon}}=\frac{m\nu}{2d} \]
donde\(\nu = 1/\sqrt{\mu\varepsilon}\) es la velocidad de un modo TEM en el medio. La longitud de onda de corte también se puede definir como
\[\label{eq:20}\lambda_{c}=\frac{\nu}{f_{c}}=\frac{2d}{m} \]
donde\(\nu\) esta la velocidad de la luz en el medio. La longitud de onda del\(\text{TM}_{m}\) modo, a una frecuencia particular, es la longitud de onda guía
\[\label{eq:21}\lambda_{g}=\frac{2\pi}{\beta}=\frac{\lambda}{\sqrt{1-(f_{c}/f)^{2}}} \]
donde\(\lambda\) es la longitud de onda de un modo TEM en el medio:\(\lambda = \nu /f\) (entonces\(\lambda_{g} =\lambda\) cuando\(k_{c} = 0\)). La velocidad de fase de los modos depende del índice de modo\(m\) a través de la frecuencia de corte:
\[\label{eq:22}v_{p}=\frac{\omega}{\beta}=\frac{\nu}{\sqrt{1-(f_{c}/f)^{2}}} \]
y la velocidad del grupo es
\[\label{eq:23}v_{g}=\frac{d\omega}{d\beta}=\nu\sqrt{1-(f_{c}/f)^{2}} \]
La velocidad de fase,\(v_{p}\), de un modo TM es mayor que\(\nu\) mientras que la velocidad de grupo,\(v_{g}\), es más lenta que\(\nu\). La velocidad del grupo es la velocidad a la que se transmite la energía y por lo tanto nunca puede ser más rápida que la velocidad de la luz,\(c\). La velocidad de fase, sin embargo, puede ser mayor que\(c\). La variación del campo del modo TM se muestra a la derecha en la Figura\(\PageIndex{2}\).
La impedancia de onda del\(\text{TM}_{m}\) modo es
\[\label{eq:24}Z_{\text{TM}}=-E_{y}/H_{x}=\frac{\beta}{\omega\varepsilon}=\frac{\beta\eta}{k} \]
Las fórmulas para la atenuación se desarrollan en [1] y la atenuación del conductor
\[\label{eq:25}\alpha_{c}=\frac{2kR_{s}}{\beta\eta d}\quad\text{(with SI units of Np/m)} \]
donde\(R_{s} = 1/(\sigma\delta_{s})\) está la resistencia superficial del conductor,\(\sigma\) es la conductividad del conductor, y\(\delta_{s}\) es la profundidad de la piel en el conductor. La atenuación debida a la pérdida dieléctrica es
\[\label{eq:26}\alpha_{d}=\frac{k^{2}\tan\delta}{2\beta}\quad\text{(with SI units of Np/m)} \]
6.3.3 Modo TE
El modo eléctrico transversal (TE) se caracteriza por\(E_{z}= 0\). Siguiendo el mismo desarrollo que para los modos TM, los campos de\(\text{TE}_{n}\) modo con\(n\) variaciones de la\(H_{z}\) son
\[\begin{align}\label{eq:27}E_{z}&=0,\: E_{y}=0,\: H_{x}=0 \\ \label{eq:28}H_{z}&=H_{0}\cos(k_{c}y)\text{e}^{-\gamma z} \\ \label{eq:29}E_{x}&=\frac{\jmath\omega\mu}{k_{c}}H_{0}\sin(k_{c}y)\text{e}^{-\gamma z} \\ \label{eq:30}H_{y}&=\frac{\gamma}{k_{c}}H_{0}\sin(k_{c}y)\text{e}^{-\gamma z}\end{align} \]
Las ecuaciones para\(k_{c},\: v_{p},\: v_{g},\: f_{c},\: \lambda_{c},\) y\(\lambda_{g}\) del\(\text{TE}_{n}\) modo son las mismas que para el\(\text{TM}_{m}\) modo considerado en la sección anterior con la sustitución del índice de modo\(m\) por\(n\),\(n = 1, 2, 3,\ldots\). (Tenga en cuenta que también\(n = 0\) es una solución pero requiere una derivación por separado, consulte el resumen de esta sección.) La variación del campo del modo TE se muestra a la derecha en la Figura\(\PageIndex{2}\).
La impedancia de onda del modo TE es
\[\label{eq:31}Z_{\text{TE}}=\frac{k\eta}{\beta} \]
Las fórmulas para la atenuación se desarrollan en [1] y la atenuación del conductor
\[\label{eq:32}\alpha_{c}=\frac{2k_{c}^{2}R_{s}}{k\beta\eta d}\quad\text{(with SI units of Np/m)} \]
donde\(R_{s} = 1/(\sigma\delta_{s})\) esta la resistencia superficial,\(\eta\), del conductor,\(\sigma\) es la conductividad del conductor, y\(\delta_{s}\) es la profundidad de la piel pf el conductor. La atenuación debida a la pérdida dieléctrica es
\[\label{eq:33}\alpha_{d}=\frac{k^{2}\tan\delta}{2\beta}\quad\text{(with SI units of Np/m)} \]
6.3.4 Resumen
El modo TEM (donde\(k_{c} = 0\)) es el mismo que el\(\text{TM}_{0}\) modo y el\(\text{TE}_{0}\) modo. Aquí las derivaciones de los modos TE y TM comenzaron con la Ecuación (6.2.25) y fueron solo soluciones para\(k_{c}\neq 0\). El desarrollo de los modos de\(0th\) orden TE y TM requiere derivación de la Ecuación (6.2.26) pero esto se hizo para el modo TEM y así no se repitió para los\(\text{TM}_{0}\) modos\(\text{TE}_{0}\) y.


