2.9: Transformaciones de filtros

Hasta el momento la discusión se ha centrado en los filtros de paso bajo. La tecnología de diseño de filtros se ha desarrollado para que el diseño de un filtro de paso bajo correspondiente sea el primer paso esencial, y esto se utiliza como prototipo para derivar un filtro con otras características. Las tres transformaciones más importantes se enumeran aquí:

1. Escala de impedancia: Un prototipo de filtro de paso bajo se hace referencia a una impedancia estándar. Por lo general\(1\:\Omega\) se utiliza, por lo que la fuente de referencia y las resistencias de carga también lo son\(1\:\Omega\). Para hacer referencia a una impedancia mayor o menor, se requiere el escalado de la impedancia de todos los elementos del filtro.
2. Escalado de frecuencia de esquina: La frecuencia de esquina de un prototipo de filtro de paso bajo se normaliza a\(1\text{ rad/s}\). Para hacer referencia a otra frecuencia, los valores de los elementos deben ser alterados para que tengan la misma impedancia a la frecuencia escalada.
3. Transformación de tipo de filtro: Estas transformaciones permiten que el circuito de un filtro de paso bajo se convierta en un circuito con una respuesta de paso de banda, parada de banda o paso alto. El concepto es que la respuesta en CC es ser replicada a frecuencia infinita para el paso alto (por lo que los condensadores se convierten en inductores, etc.); ser replicados en el centro de la banda de paso para un filtro de paso de banda (así los condensadores se convierten en un\(LC\) circuito de derivación); y ser invertidos en el centro de un filtro de tope de banda ( así los capacitores se convierten en un\(LC\) circuito en serie).

Las transformaciones se pueden realizar en cualquier orden. El punto clave es que la complejidad del diseño del circuito de paso bajo es mínima ya que el número de elementos no crece hasta que se realiza la transformación del tipo de filtro, por lo que este paso a menudo se realiza al final.

2.9.1 Transformación de impedancia

Los prototipos de paso bajo discutidos hasta ahora han sido referidos a un\(1\:\Omega\) sistema. La impedancia del sistema se puede cambiar a cualquier nivel simplemente escalando las impedancias de todos los elementos del circuito en un filtro en la misma cantidad, como se muestra en la Figura\(\PageIndex{1}\). La transformación de impedancia sigue el mismo procedimiento para todos los tipos de filtros (el procedimiento es el mismo para filtros de paso bajo, paso alto, paso de banda y de parada de banda, por ejemplo). También hay que señalar que el escalado de impedancia de una línea de transmisión es simplemente la multiplicación de la impedancia característica de la línea por el factor de escala.

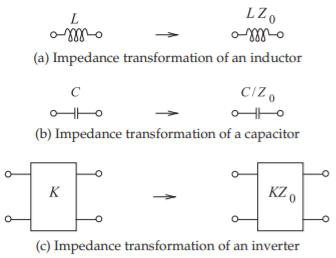
Figura\(\PageIndex{1}\): Transformaciones de impedancia. Las impedancias de los elementos se incrementan en un factor\(Z_{0}\).

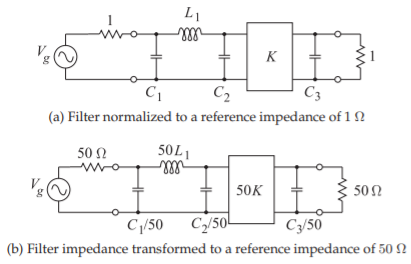
Figura\(\PageIndex{2}\): Transformación de impedancia de un filtro de ejemplo.

Ejemplo\(\PageIndex{1}\): Lowpass Filter Design

Considera el filtro de paso bajo, con un inversor, que se muestra en la Figura\(\PageIndex{2}\) (a). Se hace referencia a este filtro\(1\:\Omega\), ya que las impedancias de origen y carga son ambas\(1\:\Omega\). Rediseñar el filtro para que se obtenga la misma respuesta de frecuencia con impedancias de\(50\:\Omega\) fuente y carga.

Solución

Es necesario transformar la impedancia de\(1\:\Omega\) a\(50\:\Omega\). El filtro resultante se muestra en la Figura\(\PageIndex{2}\) (b). Cada elemento tiene una impedancia (resistencia o reactancia) que es\(50\) veces mayor que la que tenía en el\(1\:\Omega\) prototipo.

2.9.2 Transformación de frecuencia: paso bajo

Las transformaciones de frecuencia difieren según el tipo de filtro. Por lo que es normal transformar en frecuencia el prototipo de paso bajo antes de convertir el prototipo a otra forma (como el paso de banda). Los prototipos de paso bajo normalmente tienen una frecuencia de borde de banda o de corte a una frecuencia angular de unidad, es decir,\(1\text{ rad/s}\). La frecuencia de borde de banda puede transformarse de la unidad a una frecuencia angular arbitraria\(\omega_{c}\), como se muestra en la Figura\(\PageIndex{3}\), escalando los elementos reactivos, como se muestra en las Figuras\(\PageIndex{4}\) y\(\PageIndex{5}\) (a), de manera que

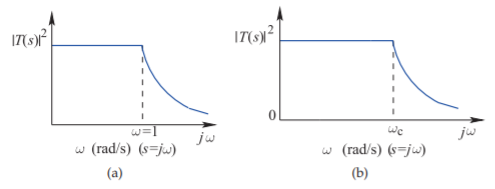
Figura\(\PageIndex{3}\): Transformación de frecuencia de una respuesta de filtro de paso bajo de (a) uno normalizado a una frecuencia de esquina de\(1\text{ rad/s}\), a (b) uno con una frecuencia de esquina de radianes de\(\omega_{c}\).

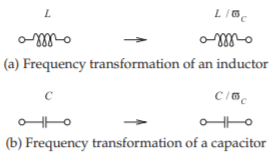
Figura\(\PageIndex{4}\): Transformaciones de frecuencia. La impedancia del nuevo elemento (escalado) a la nueva frecuencia (escalada) es la misma que en la frecuencia original.

tienen la misma impedancia a la frecuencia transformada que a la frecuencia original. El inversor se mantiene inalterado, al igual que las resistencias de fuente y carga, ya que éstas son independientes de la frecuencia.

2.9.3 Transformación de paso bajo a paso alto

La transformación de un prototipo de filtro de paso bajo en un filtro de paso alto se muestra diagramáticamente en la Figura\(\PageIndex{6}\). Matemáticamente\(\omega\) en la función de transferencia del prototipo de paso bajo se sustituye por\(−1/\omega\), es decir

\[\label{eq:1}T_{\text{highpass}}(\omega)=T_{\text{lowpass}}(-1/\omega) \]

En términos de un elemento agrupado en el circuito prototipo de paso bajo, si un elemento tiene una impedancia\(\jmath\omega L\) y\(L\) es independiente de la frecuencia, entonces el elemento correspondiente en el filtro prototipo paso alto tiene una impedancia\(1/(\jmath\omega^{2} L)\). Así, los elementos reactivos se transforman como se muestra en la Figura\(\PageIndex{5}\) (b), donde\(\omega_{0}\) está la frecuencia de esquina tanto de los circuitos prototipo de paso bajo como de paso alto. Entonces los inductores se transforman en capacitores y los capacitores en inductores. Por ejemplo, los prototipos de filtros de paso bajo de orden impares mostrados en la Figura 2.7.3 se transforman en los filtros de paso alto mostrados en la Figura\(\PageIndex{7}\).

2.9.4 Transformación de paso bajo a paso de banda

Comprender la transformación del filtro de paso bajo en su forma de paso de banda correspondiente requiere que el filtro de paso bajo sea considerado con sus respuestas de frecuencia tanto positiva como negativa, como se muestra en la Figura\(\PageIndex{8}\) (a). Esta respuesta se desplaza en frecuencia para obtener la respuesta de paso de banda mostrada en la Figura\(\PageIndex{8}\) (b). Matemáticamente la frecuencia radián,\(\omega\), en la respuesta

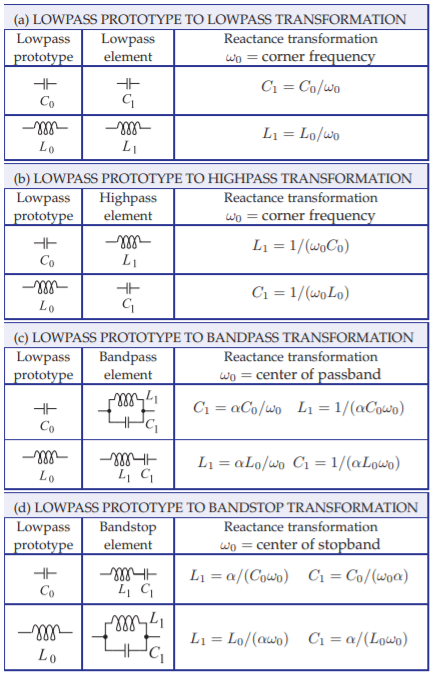
Figura\(\PageIndex{5}\): Transformaciones de los elementos de un filtro de paso bajo prototipo para obtener tipos de filtro específicos. La frecuencia de esquina del prototipo de paso bajo es\(1\text{ rad/s}\). En las transformaciones a filtros de paso de banda y de parada de banda,\(\omega_{0} = 1/\sqrt{L_{1}C_{1}} = \sqrt{\omega_{1}\omega_{2}}\);\(\omega_{1}\) y\(\omega_{2}\) son las frecuencias de borde de banda, y\(\alpha\) es la constante de transformación,\(\alpha = \omega_{0}/(\omega_{2} −\omega_{1})\).

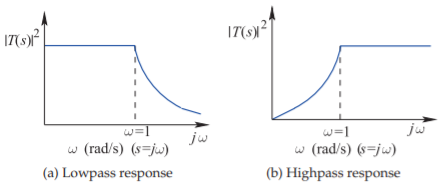
Figura\(\PageIndex{6}\): Transformación de paso bajo a paso alto.

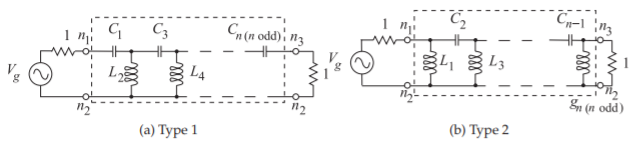
Figura\(\PageIndex{7}\): Prototipos de filtro paso alto Chebyshev de orden impares en la topología de Cauer. Aquí n es el orden del filtro.

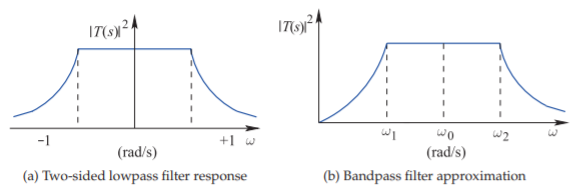
Figura\(\PageIndex{8}\): Respuestas de frecuencia en la transformación de paso bajo a paso de banda\((s =\jmath\omega)\).

se sustituye por su forma de paso de banda,

\[\label{eq:2}\omega\to\left[\frac{\omega}{\omega_{0}}-\frac{\omega_{0}}{\omega}\right] \]

Es decir,

\[\label{eq:3}T_{\text{bandpass}}(\omega)=T_{\text{lowpass}}\left(\frac{\omega}{\omega_{0}}-\frac{\omega_{0}}{\omega}\right) \]

y así la función de transferencia del filtro pasabanda se deriva de la función de transferencia del filtro pasabanda con\(\omega\) reemplazado por\((\omega /\omega_{0} −\omega_{0}/\omega )\). Esto mapea por separado las frecuencias\(+1\) de radianes\(−1\) y de borde de banda de la respuesta de paso bajo a las frecuencias de paso de banda\(\omega_{1}\) y\(\omega_{2}\):

\[\label{eq:4}-1\to\left[\frac{\omega_{1}}{\omega_{0}}-\frac{\omega_{0}}{\omega_{1}}\right]\quad\text{and}\quad +1\to\left[\frac{\omega_{2}}{\omega_{0}}-\frac{\omega_{0}}{\omega_{2}}\right] \]

Resolver las ecuaciones anteriores produce simultáneamente la frecuencia central ω0 y las frecuencias de borde de banda\(\omega_{1}\) y\(\omega_{2}\) con

\[\label{eq:5}\omega_{0}=\sqrt{\omega_{1}\omega_{2}} \]

y la llamada constante de transformación

\[\label{eq:6}\alpha=\frac{\omega_{0}}{\omega_{2}-\omega_{1}} \]

Las conversiones de elementos resultantes se dan en la Figura\(\PageIndex{5}\) (c).

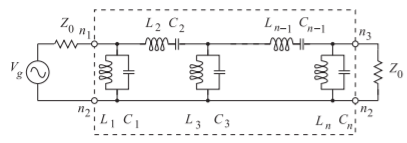
Figura\(\PageIndex{9}\): Prototipos de filtro paso banda Chebyshev de\(n\) orden impares (orden th) de elementos agrupados en la topología Cauer Tipo II.

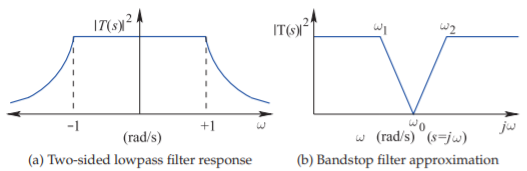
Figura\(\PageIndex{10}\): Respuestas de frecuencia en la transformación de paso bajo a parada de banda.

A modo de ejemplo, en la Figura se muestra un filtro de paso de banda Cauer de tipo 2 de elementos grumados\(\PageIndex{9}\). La\(LC\) combinación de derivación y las\(LC\) combinaciones en serie son resonadores resonantes en la frecuencia central del filtro. Aquí el filtro se normaliza a las impedancias de\(Z_{0}\) fuente y carga. Como estos son los mismos, esta topología de filtro solo se aplica para un filtro de orden impares. Combinando transformaciones, los valores de elementos de un filtro de paso de banda agrupado con frecuencia de radianes centrales\(\omega_{0} = 2\pi f_{0}\) y ancho de banda radianes\(\omega_{\text{BW}} = 2\pi (f_{2} − f_{1})\) son los siguientes (\(g_{r}\)es del prototipo de paso bajo):

\[\label{eq:7} C_{r}=\left\{\begin{array}{ll}{\frac{g_{r}}{\omega_{\text{BW}}Z_{0}}}&{r=\text{odd}} \\ {\frac{\omega_{\text{BW}}}{\omega_{0}^{2}g_{r}Z_{0}}}&{r=\text{even}}\end{array} \right. \quad\text{and}\quad L_{r}= \left\{\begin{array}{ll}{\frac{\omega_{\text{BW}}Z_{0}}{\omega_{0}^{2}g_{r}}}&{r=\text{odd}}\\{\frac{g_{r}Z_{0}}{\omega_{\text{BW}}}}&{r=\text{even}}\end{array} \right. \]

2.9.5 Transformación de paso bajo a bandstop

De nuevo, considere tanto las respuestas de frecuencia positiva como negativa del prototipo de filtro de paso bajo, como se muestra en la Figura\(\PageIndex{10}\) (a). Esta respuesta se desplaza en frecuencia para obtener la respuesta de parada de banda mostrada en la Figura\(\PageIndex{10}\) (b). Matemáticamente la frecuencia,\(\omega\), en la función de respuesta es reemplazada por su forma bandstop:

\[\label{eq:8}\omega\to\left[\alpha\left(\frac{\omega}{\omega_{0}}-\frac{\omega_{0}}{\omega}\right)\right]^{-1} \]

Es decir,

\[\label{eq:9}T_{\text{bandstop}}(\omega)=T_{\text{lowpass}}\left(\frac{1}{\alpha}\left[\frac{\omega}{\omega_{0}}-\frac{\omega_{0}}{\omega}\right]^{-1}\right) \]

La frecuencia central (correspondiente a DC en la respuesta del prototipo de paso bajo) es

\[\label{eq:10}\omega_{0}=\sqrt{\omega_{1}\omega_{2}} \]

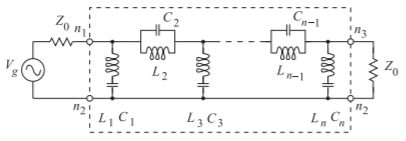
Figura\(\PageIndex{11}\): Prototipos de filtro de parada de banda Chebyshev de\(n\) orden impares de elementos agrupados (orden th) en la topología Cauer tipo II.

y la constante de transformación es

\[\label{eq:11}\alpha=\frac{\omega_{0}}{\omega_{2}-\omega_{1}} \]

donde\(\omega_{1}\) y\(\omega_{2}\) son las frecuencias de radianes de borde de banda. Las conversiones de elementos resultantes se dan en la Figura\(\PageIndex{5}\) (d).

Combinando transformaciones, los valores de elemento de un filtro de parada de banda agrupada con frecuencia de radianes central\(\omega_{0} = 2\pi f_{0}\) y ancho de banda radianes\(\omega_{\text{BW}} = 2\pi (f_{2} − f_{1})\) son los siguientes:

\[\label{eq:12}C_{r}=\left\{\begin{array}{ll}{\frac{g_{r}\omega_{\text{BW}}}{\omega_{0}^{2}Z_{0}}}&{r=\text{odd}} \\ {\frac{1}{\omega_{\text{BW}}g_{r}Z_{0}}}&{r=\text{even}}\end{array}\right.\quad\text{and}\quad L_{r}=\left\{\begin{array}{ll}{\frac{Z_{0}}{\omega_{\text{BW}}g_{r}}}&{r=\text{odd}}\\{\frac{g_{r}\omega_{\text{BW}}Z_{0}}{\omega_{0}^{2}}}&{r=\text{even}}\end{array}\right. \]

En la Figura se muestra un filtro de tope de banda Cauer tipo II de elementos grumados\(\PageIndex{11}\). La\(LC\) combinación paralela y las\(LC\) combinaciones en serie son resonadores resonantes en la frecuencia central del filtro. El\(LC\) resonador paralelo es un circuito abierto en la frecuencia central de la banda de parada y los\(LC\) resonadores en serie son cortocircuitos. Los\(LC\) resonadores se implementan usando resonadores, generalmente segmentos de línea de transmisión y no componentes agrupados.

2.9.6 Prototipos de Escalera Transformada

Combinando las transformaciones del tipo de filtro, y con el uso apropiado de los inversores, el filtro de escalera prototipo de paso bajo original y sus diversas transformaciones de tipo de filtro se muestran en la Figura 2.10.1.