2.11: Filtros de paso de banda Butterworth y Chebyshev
- Page ID
- 85182
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Los diseños de filtros Butterworth y Chebyshev con frecuencias centrales\(1\text{ GHz}\) y\(3\text{ dB}\) anchos de banda de se\(10\%\) muestran en la Figura 2.10.4. Sus respuestas de transmisión\(S_{21}\), y reflexión\(S_{11}\), se muestran en la Figura\(\PageIndex{1}\). Las faldas del filtro, es decir, las transiciones de la banda de paso a las bandas de parada, son más pronunciadas para el filtro Chebyshev que para el filtro Butterworth como se esperaba. La ondulación del filtro Chebyshev es muy pequeña y no se ve en esta trama. En un filtro real habrá pérdidas y ondulaciones de bajo nivel en la respuesta de magnitud
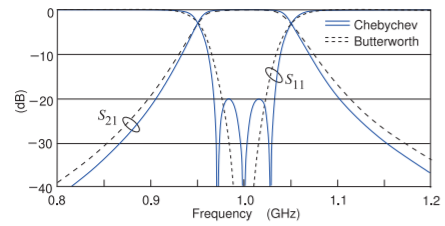
Figura\(\PageIndex{1}\): Pérdida de inserción\((S_{21})\) y pérdida\((S_{11})\) de retorno de los filtros pasabanda de elementos agrupados Butterworth y Chebychev en un\(50\:\Omega\) sistema.
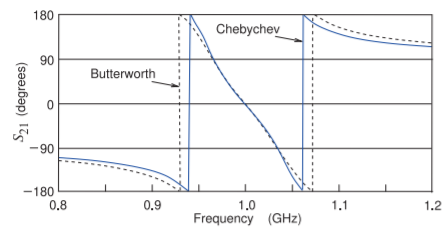
Figura\(\PageIndex{2}\): Fase de la respuesta\((S_{21})\) de transmisión de los filtros de elementos agrupados Butterworth y Chebyshev. Las discontinuidades observadas en la fase de\(−180^{\circ}\) a\(+180^{\circ}\) son artefactos y las fases de los filtros se reducen monótonamente al aumentar la frecuencia. (Por ejemplo, la fase at\(0.8\text{ GHz}\) es\(−110^{\circ} + 360^{\circ} = 250^{\circ}\).)
desaparecer. Sin embargo aún con la pérdida se mantienen las faldas empinadas de la respuesta de transmisión de Chebyshev. También, incluso con la pérdida, el impacto de las ondas de Chebyshev se ve claramente en la\((S_{11})\) respuesta de reflexión. En la Figura se ven\(\PageIndex{1}\) tres\(S_{11}\) ceros distintos y estos corresponden a los tres polos de la\(S_{21}\) respuesta del filtro Chebyshev, pero claro que no podemos verlos. (En la función de transferencia de Laplace hay polos\(3\) complejos, cada par se transforma a partir de uno de los tres polos del prototipo de paso bajo). El filtro Butterworth también tiene tres\(S_{11}\) ceros (complejos) y estos están todos en la frecuencia central del filtro de paso de banda,\(1\text{ GHz}\).
Otra característica que difiere entre las respuestas de Chebyshev y Butterworth se observa en sus respuestas de fase trazadas en la Figura\(\PageIndex{2}\). Cada polo en la\(S_{21}\) característica provoca un cambio\(90^{\circ}\) de fase. Los tres polos complejos (es decir, seis polos reales) de\(S_{21}\) entonces resultan en seis cambios de\(90^{\circ}\) fase\(S_{21}\) para un cambio de fase total de\(450^{\circ}\). Se ven pequeñas ondas en las respuestas de fase de Chebyshev en la banda de paso mientras que los cambios de fase para el filtro Butterworth son suaves. (Las ondas de la fase de Chebyshev permanecen incluso con pérdidas de bajo nivel).
Las respuestas de magnitud y fase, Figuras\(\PageIndex{1}\) y\(\PageIndex{2}\), no proporcionan una visualización completa de las características del filtro. Se proporciona información adicional en los\(S_{11}\) loci en el gráfico de Smith, ver Figura\(\PageIndex{3}\). La figura\(\PageIndex{3}\) muestra las\(S_{11}\) características trazadas en los gráficos de Smith. (En la banda de paso el\(S_{21}\) locus estaría muy cerca del círculo unitario y se observa poco valor en la banda de paso). Aquí hay una gran cantidad de información. Primero considere la respuesta para el filtro Chebyshev, Figura\(\PageIndex{3}\) (a). A medida que aumenta la frecuencia\(0.8\text{ GHz}\), el locus de primero\(S_{11}\) se acerca al círculo unitario y luego se acerca al origen
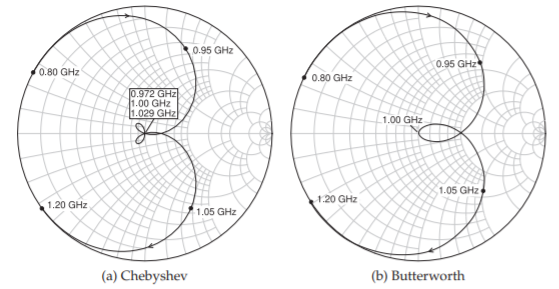
Figura\(\PageIndex{3}\): Gráfica de Smith\(S_{11}\) de los filtros de elementos agrupados Butterworth y Chebychev.
de la gráfica polar a medida que la frecuencia se acerca a la banda de paso del filtro. Una característica especial de la respuesta de Chebyshev es el bucle que aquí resulta en tres pasadas del locus a través del origen. Estos son los tres ceros. Finalmente el locus de\(S_{11}\) aumenta a medida que la frecuencia aumenta por encima de la banda de paso. También se observa un bucle en la respuesta de Butterworth, Figura\(\PageIndex{3}\) (b). Este bucle pasa por el origen y si bien parece que solo hay un cero en realidad hay tres. Lo que está sucediendo es que a medida que aumenta la frecuencia y a medida que el locus de la\(S_{11}\) respuesta de Butterworth se acerca al origen, el movimiento del locus con respecto a la frecuencia se ralentiza. La mejor manera de convencerse de que hay tres ceros de\(S_{11}\) es mirar la\((\angle S_{21})\) respuesta de fase de transmisión en la Figura\(\PageIndex{1}\).
La visualización integral de la respuesta del filtro requiere las gráficas rectangulares de las magnitudes de\(S_{21}\) y\(S_{11}\), Figura\(\PageIndex{1}\), de\(S_{21}\) fase, Figura\(\PageIndex{2}\), y la gráfica de Smith de\(S_{11}\), Figura\(\PageIndex{3}\). La gráfica de fase le convence del número de ceros en su diseño, lo cual es importante para interpretar los resultados de Butterworth. Una implementación física del diseño no será exacta y por lo tanto se requiere afinación. Entonces las caracterizaciones más importantes son la magnitud rectangular y las respuestas del gráfico Smith. Aquí los bucles en la tabla de Smith, aunque no pasen por el origen exactamente, distinguen las respuestas de Butterworth y Chebyshev. La coincidencia puede ser necesaria para desplazar los bucles al origen de la parcela polar.

