4.6: Distorsión no lineal
- Page ID
- 85131
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La distorsión impone un límite fundamental a la eficiencia que se puede realizar en un sistema de RF [24, 25, 26, 27]. Debe haber suficiente energía de CC para garantizar que las señales se procesen con no más de la distorsión máxima aceptable. La distorsión no lineal se origina cuando la señal de salida de un amplificador, por ejemplo, se acerca a los extremos de la línea de carga para que la salida no sea una replicación amplificada exacta de la señal de entrada.
4.5.1 Distorsión de amplitud y fase
Para una señal de un tono, la ganancia de amplitud de la señal se apaga a medida que aumenta la potencia de entrada, como se muestra en la Figura\(\PageIndex{1}\) (a). Esta cifra representa la potencia de la onda sinusoidal de salida frente a la potencia de la onda sinusoidal de entrada. La gráfica se llama la respuesta AM-to-AM (AM-AM) (la respuesta de amplitud dependiente de la amplitud) del amplificador. La característica AM-AM es lineal a bajas potencias de entrada, pero eventualmente la ganancia se reduce (comprime) y la potencia de salida cae por debajo de la extensión lineal de la respuesta de señal pequeña. En la Figura\(\PageIndex{1}\) (a), el punto de compresión de\(1\text{ dB}\) ganancia es el punto donde la diferencia entre la respuesta lineal extrapolada excede la ganancia real por\(1\text{ dB}\). \(P_{1\text{dB}}\)es la potencia de salida en el punto de compresión de\(1\text{ dB}\) ganancia y es la métrica de distorsión más importante, y los diseñadores de amplificadores utilizan\(P_{1\text{dB}}\) como punto de referencia.
Una compresión de ganancia de\(1\text{ dB}\) corresponde a una reducción de amplitud de voltaje de señal de\(11\%\) lo que\(P_{1\text{dB}}\) indica una reducción pequeña pero significativa en la ganancia lineal de un amplificador. Para órdenes altos de modulación, este\(11\%\) error podría significar que la señal recibida muestreada no coincide con el punto de constelación transmitido real. El rango de potencia de una señal de entrada modulada generalmente se elige de modo que la potencia pico de la envolvente sea igual o menor que la potencia de compresión de\(1\text{ dB}\) ganancia. Por lo tanto, para casi todos los formatos de modulación (una excepción notable es FM) la potencia de señal promedio se retrocede de la potencia de compresión de\(1\text{ dB}\) ganancia por la relación de potencia de envolvente pico a media (PMEPR) de la señal modulada. Con la modulación de orden superior que tiene un PMEPR más alto, se requiere un mayor retroceso.
A grandes potencias, las capacitancias parásitas de los transistores en el amplificador varían la fase de la señal de salida, y por lo tanto se produce distorsión de fase. La Figura\(\PageIndex{1}\) (b) muestra lo que se llama la característica AM a PM (AM-PM) que es una medida de la distorsión de fase dependiente de la amplitud. Para una señal modulada digitalmente, la distorsión de fase sería
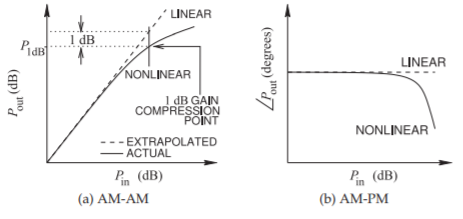
Figura\(\PageIndex{1}\): Efectos no lineales introducidos por hardware de RF: (a) distorsión de amplitud dependiente de amplitud (AM-AM); y (b) distorsión de fase dependiente de amplitud (AM-PM).
significativo si provocó que se seleccionara el punto de constelación incorrecto en un receptor. Entonces para la modulación 8-PSK un desplazamiento de\(22.5^{\circ}\) fase sería significativo, menos si se considera ruido. La distorsión AM-AM generalmente ocurre antes de que la fase de salida varíe apreciablemente. Esto se debe a que la no linealidad de un transistor es predominantemente una no linealidad de corriente-voltaje con distorsión de fase que proviene principalmente de la no linealidad de las capacitancias parásitas.
Si bien la Figura\(\PageIndex{1}\) presenta las características de distorsión para una sola onda sinusoidal, ha demostrado ser un indicador razonable de rendimiento con señales moduladas. En particular, siendo la potencia de salida máxima de la envolvente máxima\(P_{1\text{dB}}\), la distorsión en banda suele ser aceptable mientras se maximiza la alta eficiencia del amplificador [28].
Las caracterizaciones AM-AM y AM-PM describen la distorsión con un amplificador pero también se utilizan con otros tipos de subsistemas no lineales como los mezcladores.
Ejemplo\(\PageIndex{1}\): Amplifer Back-Off
Un amplificador tiene una potencia de salida de\(10\text{ dBm}\) cuando la ganancia de un solo tono es comprimida por\(1\text{ dB}\). ¿Cuál es la potencia de salida máxima de una señal QPSK no distorsionada con un PMEPR de\(3.6\text{ dB}\)?
Solución
La señal QPSK de salida máxima no distorsionada se acepta generalmente como cuando la potencia máxima de la envolvente es igual a la potencia de compresión de\(1\text{ dB}\) ganancia. En dBm, la potencia de envolvente pico es mayor que la potencia de señal media por la relación de potencia de envolvente pico a media. Por lo tanto, se dice que la potencia de la señal QPSK está retrocedida desde el punto de compresión de\(1\text{ dB}\) ganancia por PMEPR. Por lo tanto, la potencia de salida máxima no distorsionada de la señal QPSK es
\[\label{eq:1}P_{o,\text{QPSK}}=P_{1\text{dB}}|_{\text{dBm}}-\text{PMEPR}|_{\text{dB}}=10\text{ dBm}-3.6\text{ dB}=6.4\text{ dBm} \]
4.5.2 Compresión de ganancia
El voltaje\(v_{o}(t)\) en la salida de un amplificador que está polarizado en el medio de las características de voltaje de corriente de salida (es decir, un amplificador de Clase A) se puede modelar por los primeros términos de una serie Taylor
\[\label{eq:2}v_{o}(t)=a_{0}+a_{1}v_{i}(t)+a_{2}v_{i}^{2}(t)+a_{3}v_{i}^{3}(t)+\ldots \]
donde\(v_{i}(t)\) esta el voltaje de entrada. En un amplificador de Clase A, los términos de orden par son pequeños porque la distorsión en los extremos de la forma de onda de voltaje son en gran parte simétricos, y se encuentra que los coeficientes de los términos de orden impar de la serie Taylor disminuyen rápidamente de manera que\(|a_{1}|≫|a_{3}|≫|a_{5}|\ldots\). También se encuentra que\(a_{3}\) es negativo. Con un solo voltaje de entrada sinusoidal en frecuencia\(f_{1} = \omega_{1}/(2\pi)\),\(v_{i}(t) = V_{1} \cos(\omega_{1}t)\) y el voltaje de salida es
\[\begin{align}v_{o}(t)&=a_{0}+a_{1}V_{i}\cos(\omega_{1}t)+a_{2}V_{1}^{2}\cos^{2}(\omega_{1}t)+a_{3}V_{i}^{3}\cos^{3}(\omega_{1}t)+\ldots\nonumber \\ &=(a_{0}+\frac{1}{2}a_{2}V_{i}^{2})+(a_{1}V_{i}+\frac{3}{4}a_{3}V_{i}^{3})\cos(\omega_{1}t)\nonumber \\ \label{eq:3}&\quad+\frac{1}{2}a_{2}V_{i}^{2}\cos(2\omega_{1}t)+\frac{1}{4}a_{3}V_{i}^{3}\cos(3\omega_{1}t)+\ldots\end{align} \]
Los amplificadores de RF y microondas se utilizan con filtros pasabanda y la distorsión correspondiente a los armónicos se filtra fácilmente. Así, la salida, después de filtrar y retirar el componente de CC es
\[\label{eq:4}v_{o}(t)=(a_{1}V_{i}+\frac{3}{4}a_{3}V_{i}^{3})\cos(\omega_{1}t)=V_{o}\cos(\omega_{1}t) \]
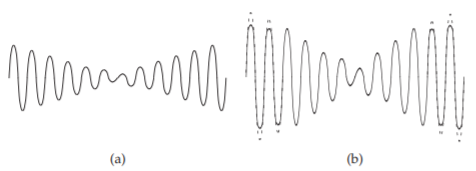
Figura\(\PageIndex{2}\): Una señal de dos tonos: (a) una forma de onda de entrada de dos tonos; y (b) salida distorsionada que muestra compresión (la forma de onda discontinua no está distorsionada).
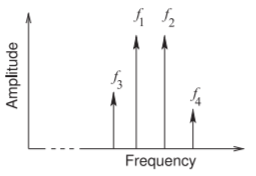
Figura\(\PageIndex{3}\): Espectro en la salida de un amplificador no lineal con una señal de entrada de dos tonos. Este es el espectro de la forma de onda en la Figura\(\PageIndex{2}\). Numéricamente\(f_{3} = 2f_{1} − f_{2}\) y\(f_{4} = 2f_{2} − f_{1}\).
donde\(V_{o} = a_{1}V_{i} + \frac{3}{4}a_{3}V_{i}^{3}\) es la magnitud de la tensión a la frecuencia de entrada. Entonces la ganancia de voltaje es
\[\label{eq:5}^{V}G=\frac{V_{o}}{V_{i}}=a_{1}+\frac{3}{4}a_{3}V_{i}^{2} \]
y la ganancia de potencia (suponiendo que las impedancias de entrada y salida son las mismas)
\[\label{eq:6}G=\:^{V}G^{2} \]
Dado que\(a^{3}\) es negativa, la ganancia para voltajes de entrada muy bajos, pequeños\(V_{1}\), es lineal con\(^{V}G = a_{1}\) y la ganancia se reduce para señales de entrada más grandes, resultando en la compresión de ganancia, la reducción en la pendiente de\(P_{\text{out}}\) versus\(P_{\text{in}}\), se ve en la Figura\(\PageIndex{1}\) (a). Para otros amplificadores, y particularmente para los amplificadores de conmutación, se deben considerar muchos más términos en la expansión de la serie de potencia, y es posible que la ganancia pueda aumentar antes de caer y eventualmente saturarse. Este incremento temporal en la ganancia se denomina expansión de ganancia.
4.5.3 Distorsión de intermodulación
Una señal de dos tonos que consta de dos señales sinusoidales es una mejor representación del rendimiento del sistema con señales moduladas. Una señal que es la combinación lineal de dos señales sinusoidales de igual amplitud se muestra en la Figura\(\PageIndex{2}\) (a). Cuando esta señal es grande y se introduce en un amplificador en lo que se denomina prueba de dos tonos, se comprimen los extremos de la señal de salida. Esto da como resultado la forma de onda de salida saturada mostrada en la Figura\(\PageIndex{2}\) (b), donde la curva discontinua es la forma de onda no distorsionada. En el dominio de la frecuencia esta distorsión produce tonos adicionales de manera que se dice que esta distorsión produce productos de intermodulación (IMPs), como se muestra en la Figura\(\PageIndex{1}\). Aquí los\(f_{2}\) componentes\(f_{1}\) y tienen las frecuencias de la señal de entrada original de dos tonos. Los tonos extra en la salida,\(f_{3}\) y\(f_{4}\), son los tonos de intermodulación. El tono at\(f_{3} = 2f_{1} − f_{2}\) se conoce como el tono IM3 inferior (o intermod inferior de tercer orden) y el tono en\(f_{4} = 2f_{2} − f_{1}\) se conoce como el tono IM3 superior.
La forma más sencilla de ver la distorsión de intermodulación es considerar una señal de entrada de dos tonos,
\[\label{eq:7}v_{i}(t)=V_{i}[\cos(\omega_{1}t)+\cos(\omega_{2}t)] \]
donde los tonos a frecuencias\(f_{1} = \omega_{1}/(2\pi )\) y\(f_{2} = \omega_{2}/(2\pi)\) tienen igual amplitud\(V_{i}\). Sustituir esta señal en la expansión de la serie Taylor en Ecuación\(\eqref{eq:2}\) conduce a la señal de salida
\[\begin{align}v_{o}(t)&=a_{0}+a_{1}V_{i}\cos(\omega_{1}t)+a_{1}V_{i}\cos(\omega_{2}t)+\frac{1}{2}a_{2}V_{i}^{2}[\cos(\omega_{1}t)+\cos(\omega_{2}t)]^{2}\nonumber \\ &\quad +a_{3}V_{i}^{3}[\cos(\omega_{1}t)+\cos(\omega_{2}t)]^{3}+\ldots\nonumber \\ &=a_{0}+a_{1}V_{i}\cos(\omega_{1}t)+a_{1}V_{i}\cos(\omega_{2}t)+\frac{1}{2}a_{2}V_{i}^{2}[1+\cos(2\omega_{1}t)]\nonumber \\ &\quad +\frac{1}{2}a_{2}V_{i}^{2}[1+a_{1}\cos(2\omega_{2}t)]+a_{2}V_{i}^{2}\cos(\omega_{1}-\omega_{2})t+a_{2}V_{i}^{2}\cos(\omega_{1}+\omega_{2})t\nonumber \\ &\quad +a_{3}V_{i}^{3}[\frac{3}{4}\cos(\omega_{1}t)+\frac{1}{4}\cos(3\omega_{1}t)]+a_{3}V_{i}^{3}(\frac{3}{4}\cos(\omega_{2}t)+\frac{1}{4}\cos(3\omega_{2}t)]\nonumber \\ &\quad +a_{3}V_{i}^{3}[\frac{3}{2}\cos(3\omega_{1}t)+\frac{3}{4}\cos(2\omega_{2}-\omega_{1})t+\frac{3}{4}\cos(2\omega_{2}+\omega_{1})t]\nonumber \\ \label{eq:8}&\quad+ a_{3}V_{i}^{3}[\frac{3}{2}\cos(3\omega_{2}t)+\frac{3}{4}\cos(2\omega_{1}-\omega_{2})t+\frac{3}{4}\cos(2\omega_{1}+\omega_{2})t]+\ldots\end{align} \]
El componente de la salida en la primera fundamental es
\[\label{eq:9}V_{o,1}=a_{1}V_{i}+\frac{3}{4}a_{3}V_{i}^{3} \]
y el componente de la salida en el segundo fundamental es
\[\label{eq:10}V_{o,2}=a_{1}V_{i}+\frac{3}{4}a_{3}V_{i}^{3} \]
Tenga en cuenta que\(a_{1}\) es la ganancia de voltaje lineal del amplificador:
\[\label{eq:11}a_{1}=V_{o,1}/V_{i}=V_{o,2}/V_{i} \]
4.5.4 Distorsión de tercer orden
Los amplificadores de RF y microondas se usan típicamente con redes o filtros de coincidencia entre etapas de paso de banda o paso bajo, y así se filtra la distorsión correspondiente a los armónicos. Sin embargo, los tonos en frecuencia\(f_{3} = 2f_{1} − f_{2} = \omega_{3}/(2\pi)\) y\(f_{4} = 2f_{1} − f_{2} = \omega_{4}/(2\pi )\) estarán dentro de la banda de paso del amplificador si f1 y f2 están cerca. La aparición de estos tonos indica distorsión de tercer orden, ya que la distorsión es el resultado de términos de tercer orden en la expansión de la serie de potencia de la característica de entrada-salida de dos tonos como se indica en la Ecuación\(\eqref{eq:8}\). Es decir, la salida después de filtrar y quitar el componente de CC es
\[\label{eq:12}v_{o}(t)=V_{0,1}\cos(\omega_{1}t)+V_{o,2}\cos(\omega_{2}t)+V_{o,3}\cos(\omega_{3}t)+V_{o,4}\cos(\omega_{4}t) \]
donde el componente de la salida
\[\begin{align}\label{eq:13}\text{at the first fundamental, }f_{1},\text{ is }V_{o,1}&=a_{1}V_{i}+\frac{3}{4}a_{3}V_{i}^{3}\\ \label{eq:14}\text{at the second fundamental, }f_{2},\text{ is }V_{o,2}&=a_{1}V_{i}+\frac{3}{4}a_{3}V_{i}^{3} \\ \label{eq:15}\text{at the lower intermodulation frequency, }f_{3},\text{ is }V_{o,3}&=\frac{3}{4}a_{3}V_{i}^{3} \\ \label{eq:16}\text{at the upper intermodulation frequency, }f_{4},\text{ is }V_{o,4}&=\frac{3}{4}a_{3}V_{i}^{3}\end{align} \]
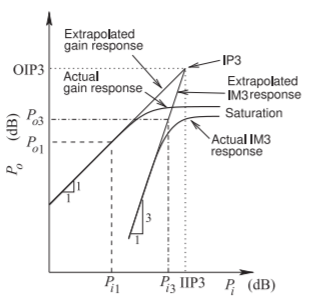
Figura\(\PageIndex{4}\): Potencia de salida versus potencia de entrada de un amplificador trazado en una escala logarítmica. La respuesta IM3 es resultado de la intermodulación de dos tonos, y la potencia de entrada es la potencia de cada una de las dos señales que tienen igual amplitud. Extrapolaciones de la respuesta fundamental\(1:1\) lineal y la respuesta de intermodulación de\(3:1\) tercer orden se cruzan en el punto IP3.
Así, el nivel de los tonos de intermodulación, el nivel IMD, aumenta como la tercera potencia del nivel de la señal de entrada de dos tonos. Dado que los niveles de IMD varían como la tercera potencia del nivel de tono de entrada (\(V_{i}\)), es habitual referirse a los tonos en\(f_{3}\) y\(f_{4}\) como intermods de tercer orden, o tonos IM3. Las respuestas de un tono e IM3 se representan en la Figura\(\PageIndex{4}\) hasta la saturación, donde los términos de orden superior en la expansión de Taylor adquieren importancia.
La relación entre la amplitud de los tonos de intermodulación y la amplitud de los tonos de entrada (recuerde que tienen igual amplitud) permite calcular el coeficiente de serie de potencias de tercer orden. Eso es
\[\label{eq:17}a_{3}=\frac{4}{3}\frac{V_{o,3}}{V_{i}^{3}}=\frac{4}{3}\frac{V_{o,4}}{V_{i}} \]
Las respuestas de ganancia e IM3 mostradas en la Figura\(\PageIndex{4}\) se representan en una escala logarítmica. Primero considere la respuesta de ganancia, que se traza para una sola entrada de onda sinusoidal. A niveles bajos de potencia de entrada el amplificador tiene ganancia lineal y la potencia de salida,\(P_{o1}\), aumenta en proporción a la potencia de entrada\(P_{i1}\), por lo que la respuesta de ganancia tiene una\(1:1\) pendiente. A medida que la potencia de entrada aumenta aún más, la potencia de salida se satura principalmente porque la forma de onda en la salida está restringida por los límites establecidos por los rieles de alimentación y tierra, pero otras no linealidades del transistor impactan en la linealidad de la respuesta antes de que se alcance la saturación. La respuesta IM3 (ya sea el nivel del\(f_{3}\) tono o el\(f_{4}\) tono) en la Figura\(\PageIndex{4}\) es cuando los niveles de dos tonos discretos son iguales. Entonces típicamente las respuestas de los tonos IM3 superior e inferior son las mismas a menos que los efectos capacitivos lleguen a ser importantes [29, 30, 31, 32]. En niveles bajos de los dos tonos de entrada, cada uno con potencia\(P_{i3}\), la potencia de salida,\(P_{o3}\), en uno de los tonos IM3 aumenta a medida que la tercera potencia de\(P_{i3}\). Así, en una escala logarítmica la pendiente de\(P_{o3}\) versus\(P_{i3}\) es\(3:1\). A medida que aumenta la potencia de entrada, la respuesta IP3 eventualmente se satura. Las dos caracterizaciones más simples de la respuesta no lineal de un amplificador son la potencia de compresión de\(1\text{ dB}\) ganancia, como se discutió anteriormente, y la intercepción de las respuestas de ganancia e IP3. Esta intersección se denomina punto de intercepción de tercer orden, o punto IP3 (ver Figura\(\PageIndex{4}\)). La potencia de entrada en IP3 se denomina potencia de intercepción de tercer orden de entrada, o IIP3, y la salida se denomina potencia de intercepción de tercer orden de salida, u OIP3. Si\(G\) es la ganancia de potencia lineal,\(\text{OIP3} = G\cdot \text{IIP3}\). IIIP3 se usa principalmente con receptores y OIP3 se usa con transmisores.
4.5.5 Recrecimiento espectral
La distorsión con señales moduladas digitalmente consiste en distorsión dentro y fuera de banda. La generación de distorsión de intermodulación en banda (dentro del ancho de banda de la señal modulada digitalmente) en un amplificador, o cualquier otro dispositivo no lineal como un mezclador, afecta la capacidad de resolver la constelación de una señal recibida. Por lo tanto, la distorsión generada en banda afecta la capacidad de interpretar la constelación de la señal y, por lo tanto, causa errores de bit. Sin embargo, la fase de los productos de intermodulación es de poca preocupación excepto en sistemas en cascada donde la fase afecta cómo se combina la distorsión IMD de diferentes etapas.
La distorsión fuera de banda se representa en la Figura\(\PageIndex{5}\), donde se muestran los espectros en la entrada y salida de un sistema no lineal. El proceso que da como resultado un aumento de los niveles de señal en las bandas laterales adyacentes se denomina rebrote espectral. Esta distorsión es similar a la distorsión de intermodulación con una señal de dos tonos. La generación de señales en el canal adyacente afecta la función de otras radios y el nivel permisible de estas señales está contenido en las especificaciones del sistema.
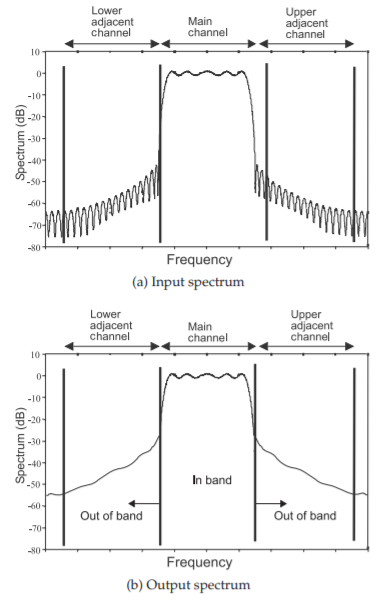
Figura\(\PageIndex{5}\): Espectros en la entrada y salida de un amplificador con una señal modulada digitalmente.
4.5.6 Distorsión de segundo orden
La subsección anterior discutió la distorsión de intermodulación e introdujo el punto de intercepción de tercer orden, IP3, definido por la potencia referida a entrada de IP3, IIP3, o la potencia referida a salida de IP3, OIP3, para caracterizar el rendimiento no lineal de tercer orden. El mismo tipo de análisis se puede utilizar para caracterizar el rendimiento no lineal de segundo orden de un módulo de microondas. La distorsión de segundo orden conduce al segundo armónico de los tonos de entrada y a la frecuencia de diferencia de los tonos de entrada. Los componentes de la respuesta de salida del amplificador en Ecuación\(\eqref{eq:8}\) en la segunda frecuencia armónica y diferencia son:
\[\label{eq:18}v_{0}(t)=V_{0,2\text{nd},1}\cos(2\omega_{1}t)+V_{0,2\text{nd},2}\cos(2\omega_{2}t)+V_{o,\text{diff}}\cos(\omega_{2}-\omega_{1}t) \]
donde la amplitud en la salida en
\[\begin{align}\text{second harmonic of }f_{1}\text{ is }V_{0,2\text{nd},1}&=\frac{1}{2}a_{2}V_{i}^{2}\nonumber \\ \text{second harmonic of }f_{2}\text{ is }V_{0,2\text{nd},2}&=\frac{1}{2}a_{2}V_{i}^{2}\nonumber \\ \label{eq:19}\text{difference frequency }f_{2}-f_{1}\text{ is }V_{0,\text{diff}}&=\frac{1}{2}a_{2}V_{i}^{2}\end{align} \]
Así, el coeficiente del término de segundo orden en el polinomio definitorio se puede obtener a partir de la amplitud de cualquiera de los segundos armónicos o del tono de diferencia.
\[\label{eq:20}a_{2}=2\frac{V_{0,2\text{nd},1}}{V_{i}^{2}}=2\frac{V_{0,2\text{nd},2}}{V_{i}^{2}}=2\frac{V_{0,\text{niff}}}{V_{i}^{2}} \]
Las respuestas de ganancia e IM2 mostradas en la Figura 4.6.1 se representan en una escala logarítmica. A niveles bajos de potencia de entrada el amplificador tiene una ganancia lineal e inicialmente la respuesta de ganancia tiene una\(1:1\) pendiente. La respuesta IM2 (ya sea los niveles de los segundos tonos armónicos o del tono de diferencia) en la Figura 4.6.1 es cuando los niveles de dos tonos discretos son los mismos. A niveles bajos de los dos tonos de entrada, cada uno con potencia\(P_{i2}\), la potencia de salida,\(P_{o2}\), en uno de los tonos armónicos o de diferencia aumenta a medida que la cuadrática de\(P_{i32}\). Así, en una escala logarítmica la pendiente de\(P_{o2}\) versus\(P_{i2}\) es\(2:1\). A medida que aumenta la potencia de entrada, la respuesta IP2 eventualmente se satura. Las caracterizaciones más simples de la respuesta no lineal de segundo orden de un amplificador son la respuesta IP2 y el punto de intercepción IP2, el punto de intercepción de segundo orden. La potencia de entrada en IP2 se denomina potencia de intercepción de segundo orden de entrada, o IIP2, y la salida se denomina potencia de intercepción de segundo orden de salida, u OIP2.
4.5.7 Resumen
Las tres caracterizaciones más simples del rendimiento de un amplificador son la ganancia lineal, la potencia de entrada o salida en el punto de intercepción IM2, IP2, y la potencia de entrada o salida en el punto de intercepción IM3, IP3, ver Figuras 4.6.1 y 4.6.2. De estos se pueden derivar los tres primeros coeficientes de un modelo polinómico de un amplificador. El primero,\(a_{1}\), proviene de la ganancia lineal, ver. El segundo,\(a_{2}\), proviene del nivel de los armónicos o tonos de diferencia para una señal de entrada de dos tonos, ver Ecuación\(\eqref{eq:20}\). El tercero,\(a_{3}\) proviene del nivel de tonos de intermodulación de tercer orden, ver Ecuación\(\eqref{eq:17}\).

