1.5: Las leyes de los grandes números

De la misma manera, para\(\tilde{p}<p\),

\[\left.\lim _{n \rightarrow \infty} \frac{\ln \operatorname{Pr}\left\{S_{n} \leq n \tilde{p}\right\}}{n}=\left[\tilde{p} \ln \frac{p}{\tilde{p}}+\tilde{q} \ln \frac{q}{\tilde{q}}\right]\right\} \quad \text { where } \tilde{p}<p\label{1.72} \]

En otras palabras, estos límites de Chernoff no solo son límites superiores, sino que también son exponencialmente correctos en el sentido de\ ref {1.71} y (1.72). En el Capítulo 7 mostraremos que esta propiedad es típica de sumas de IID rv. Así vemos que los límites de Chernoff no son 'sólo límites', sino que son límites que al optimizarse proporcionan el correcto exponente asintótico para las colas de la distribución de sumas de IID rv, en este sentido estos límites son muy diferentes de los límites de Markov y Chebyshev.

Las leyes de los números grandes son una colección de resultados en teoría de probabilidad que describen el comportamiento del promedio aritmético de\(n\) rv para grandes\(n\). Para cualquier\(n\) rv,\(X_{1}, \ldots, X_{n}\), el promedio aritmético es el rv\((1 / n) \sum_{i=1}^{n} X_{i}\). Ya que en cualquier resultado del experimento, el valor muestral de esta rv es el promedio aritmético de los valores muestrales de\(X_{1}, \ldots, X_{n}\), esta variable aleatoria suele llamarse promedio muestral. Si\(X_{1}, \ldots, X_{n}\) se ven como variables sucesivas en el tiempo, este promedio de muestra se denomina promedio de tiempo. Bajo supuestos bastante generales, la desviación estándar del promedio muestral va a 0 con el aumento\(n\), y, de diversas maneras dependiendo de los supuestos, el promedio muestral se acerca a la media.

Estos resultados son fundamentales para el estudio de los procesos estocásticos, ya que permiten relacionar los promedios de tiempo (es decir, el promedio a lo largo del tiempo de las trayectorias de muestra individuales) con los promedios del conjunto (es decir, la media del valor del proceso en un momento dado). En esta sección, desarrollamos y discutimos dos de estos resultados, la ley débil y la fuerte de los grandes números para rv independientes distribuidos idénticamente. La ley fuerte requiere una paciencia considerable para comprender, pero es un resultado básico y esencial para comprender los procesos estocásticos. También discutimos el teorema del límite central, en parte porque mejora nuestra comprensión de la ley débil, y en parte por su importancia por derecho propio.

Ley débil de grandes números con varianza finita

\(X_{1}, X_{2}, \ldots, X_{n}\)Sea IID rv con media finita\(\bar{X}\) y varianza finita\(\sigma_{X}^{2}\). Dejar\(S_{n}=X_1+\dots+X_n\), y considerar el promedio muestral\(S_{n} / n\). Vimos en\ ref {1.42} eso\(\sigma_{S_{n}}^{2}=n \sigma_{X}^{2}\). Por lo tanto, la varianza de\(S_{n} / n\) es

\[\operatorname{VAR}\left[\frac{S_{n}}{n}\right]^{\}}= \mathrm{E}\left[\left(\frac{S_{n}-n \bar{X}}{n}\right)^{\}2}\right]^{\}}=\frac{1}{n^{2}} \mathrm{E}\left[\left(S_{n}-n \bar{X}\right)^{2}\right]^{\}}=\frac{\sigma_{X}^{2}}{n}\label{1.73} \]

Esto dice que la desviación estándar del promedio muestral\(S_{n} / n\) es\(\sigma / \sqrt{n}\), que se acerca a 0 a medida que\(n\) aumenta. La Figura 1.10 ilustra esta disminución en la desviación estándar de\(S_{n} / n\) con el aumento\(n\). En contraste, recordemos que la Figura 1.5 ilustró cómo la desviación estándar de\(S_{n}\) aumenta con\(n\). Desde (1.73), vemos que

\[\lim _{n \rightarrow \infty} \mathrm{E}\left[\left(\frac{S_{n}}{n}-\bar{X}\right)^{2}\right]^{\}}=0\label{1.74} \]

En consecuencia, decimos que\(S_{n} / n\) converge en media cuadrática a\(\bar{X}\).

Figura 1.10: La misma distribución que la Figura 1.5, escalada de manera diferente para dar la función de distribución del promedio muestral\(Y_{n}\). Se puede visualizar que a medida que\(n\) aumenta, la función de distribución de\(Y_{n}\) se acerca cada vez más a un paso unitario en la media, 0.25, de las variables\(X\) que se suman.

Esta convergencia en el cuadrado medio dice que el promedio muestral,\(S_{n} / n\), difiere de la media,\(\bar{X}\), por una variable aleatoria cuya desviación estándar se acerca a 0 con el incremento\(n\). Esta convergencia en el cuadrado medio es un sentido en el que se\(S_{n} / n\) aproxima\(\bar{X}\), pero la idea de una secuencia de rv (es decir, una secuencia de funciones) que se aproxima a una constante está claramente mucho más involucrada que una secuencia de números que se aproxima a una constante. Las leyes de grandes números sacan a relucir esta idea central de una manera más fundamental, y generalmente más útil. Iniciamos el desarrollo aplicando la desigualdad de Chebyshev\ ref {1.56} al promedio muestral,

\[\operatorname{Pr}\left\{\left|\frac{S_{n}}{n}-\bar{X}\right|>\epsilon\right\}^{\}} \leq \frac{\sigma^{2}}{n \epsilon^{2}}\label{1.75} \]

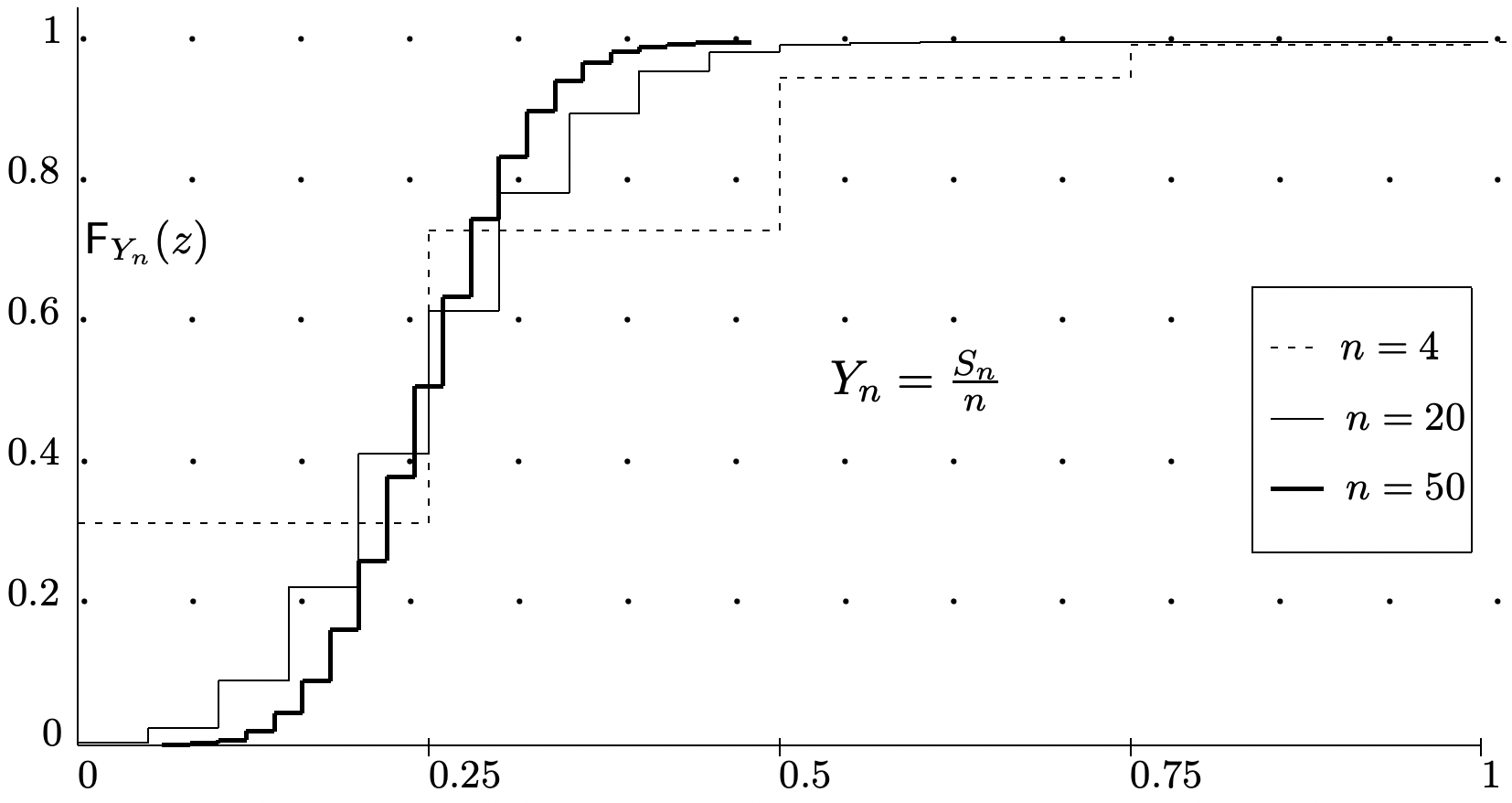
Este es un límite superior sobre la probabilidad que\(S_{n} / n\) difiere en más que\(\epsilon\) de su media,\(\bar{X}\). Esto se ilustra en la Figura 1.10 que muestra la función de distribución de\(S_{n} / n\) para varios\(n\). La cifra sugiere que\(\lim _{n \rightarrow \infty} \mathrm{F}_{S_{n} / n}(y)=0\) para todos\(y<\bar{X}\) y\(\lim _{n \rightarrow \infty} \mathrm{F}_{S_{n} / n}(y)=1\) para todos\(y>\bar{X}\). Esto se afirma más limpiamente en la siguiente ley débil de grandes números, abreviada WLLN

Teorema 1.5.1 (WLLN con varianza finita). Para cada entero\(n \geq 1\), deja\(S_{n}=X_{1}+\dots+X_n\) ser la suma de\(n\) IID rv con una varianza finita. Entonces se sostiene lo siguiente:

\[\lim _{n \rightarrow \infty} \operatorname{Pr}\left\{\left|\frac{S_{n}}{n}-\bar{X}\right|>\epsilon\right\}^{\}}=0 \quad \text { for every } \epsilon>0\label{1.76} \]

Prueba: Para cada\(\epsilon>0\),\(\operatorname{Pr}\left\{\left|S_{n} / n-\bar{X}\right|>\epsilon\right.\) está delimitada entre 0 y\(\sigma^{2} / n \epsilon^{2}\). Dado que el límite superior va a 0 con el aumento\(n\), se prueba el teorema.

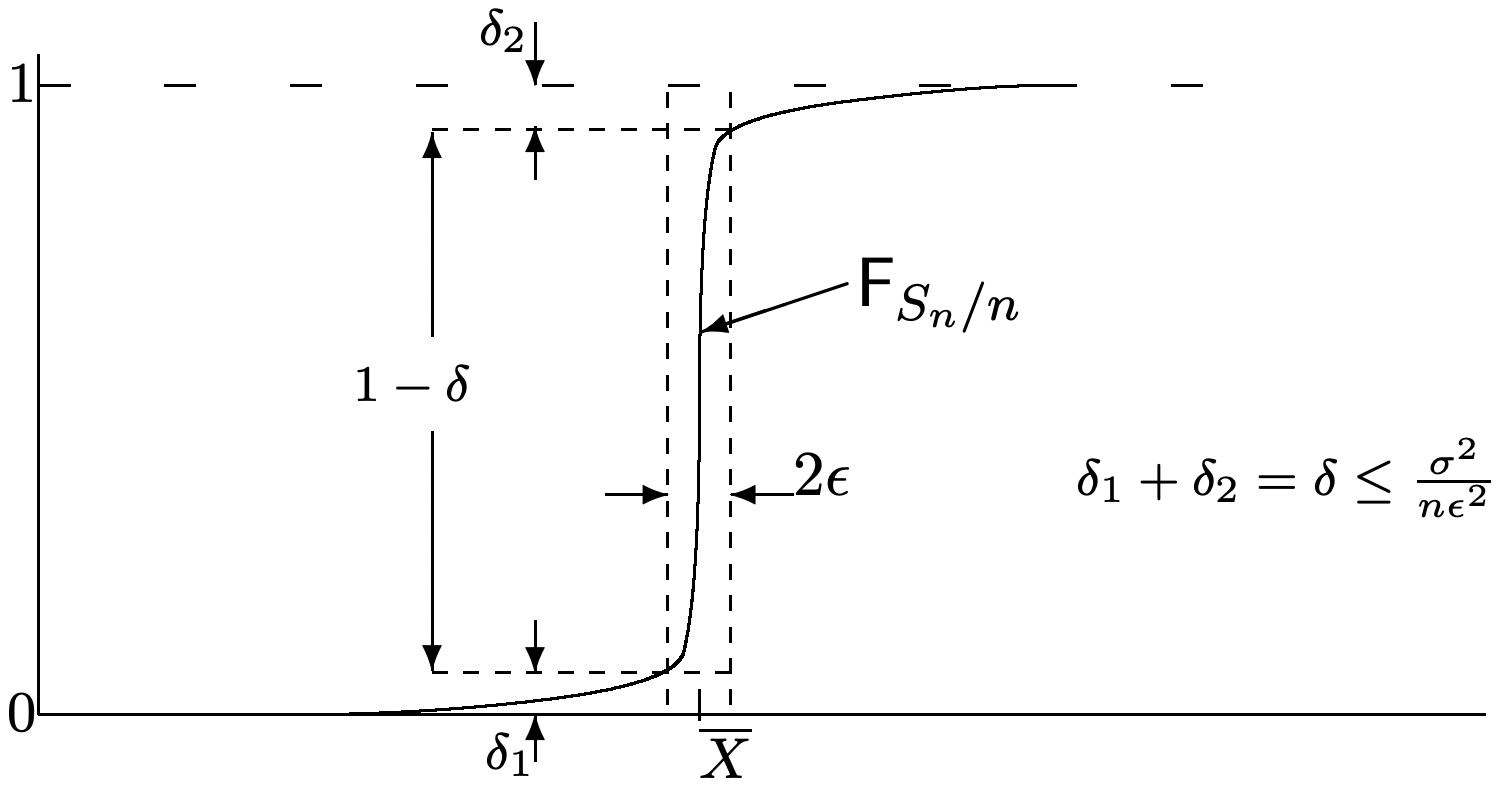
Discusión: La prueba algebraica anterior es a la vez simple y rigurosa. Sin embargo, el argumento geométrico en la Figura 1.11 probablemente proporciona más intuición sobre cómo se lleva a cabo el límite. Es importante entender ambos.

Figura 1.11: Aproximación de la función\(\mathrm{F}_{S_{n} / n}\) de distribución de un promedio muestral por una función escalonada a la media: De (1.75), la probabilidad\(\delta\) que\(S_{n} / n\) difiere de\(\bar{X}\) en más de\(\epsilon\) (es decir,\(\operatorname{Pr}\left\{\left|S_{n} / n-\bar{X}\right| \geq \epsilon\right.\)) es como máximo\(\sigma^{2} / n \epsilon^{2}\). El evento complementario, donde\(\left|S_{n} / n-\bar{X}\right|<\epsilon\), tiene probabilidad\(1-\delta \geq 1-\sigma^{2} / n \epsilon^{2}\). Esto significa que podemos construir un rectángulo de ancho\(2 \epsilon\) centrado sobre\(\bar{X}\) y de altura\(1-\delta\) tal que\(\mathrm{F}_{S_{n} / n}\) entre en el rectángulo en la parte inferior izquierda (digamos at\(\left(\bar{X}-\epsilon, \delta_{1}\right)\)) y salga en la parte superior derecha, digamos en\(\left(\bar{X}+\epsilon, 1-\delta_{2}\right)\)). Ahora visualice el aumento\(n\) mientras se mantiene\(\epsilon\) fijo. En el límite,\(1-\delta \rightarrow 1\) entonces\(\operatorname{Pr}\left\{\left|S_{n} / n-\bar{X}\right| \geq \epsilon \quad \rightarrow 0\right.\). Dado que esto es cierto para cada\(\epsilon>0\) (generalmente con convergencia más lenta a medida que\(\epsilon\) se hace más pequeño), se\(\mathrm{F}_{S_{n} / n}(y)\) acerca a 0 para cada\(y<\bar{X}\) y se acerca a 1 para cada\(y>\bar{X}\), es decir,\(\mathrm{F}_{S_{n} / n}\) se acerca a un paso unitario en\(\bar{X}\). Tenga en cuenta que aquí hay dos 'factores de fudge ',\(\epsilon\) y\(\delta\) y, dado que estamos aproximando una función de distribución completa, ninguno de los dos puede omitirse, excepto yendo directamente a un límite as\(n \rightarrow \infty\).

Nos referimos a\ ref {1.76} como decir que\(S_{n} / n\) converge\(\bar{X}\) en probabilidad. Para darle sentido a esto, debemos ver\(\bar{X}\) como una variable aleatoria determinista, es decir, una rv que toma el valor\(\bar{X}\) para cada punto de muestra del espacio. Entonces\ ref {1.76} dice que la probabilidad de que la diferencia absoluta,\(\left|S_{n} / n-\bar{X}\right|\), supere cualquier dada\(\epsilon>0\) va a 0 as\(n \rightarrow \infty\). ³¹

Uno debería preguntarse en este punto qué se suma\ ref {1.76} al límite más específico en (1.75). En particular\ ref {1.75} proporciona un límite superior sobre la tasa de convergencia para el límite en (1.76). La respuesta es que\ ref {1.76} sigue siendo válido cuando se generaliza el teorema. Para variables que no son IID o tienen una varianza infinita,\ ref {1.75} ya no es necesariamente válida. En algunas situaciones, como veremos más adelante, es valioso saber que\ ref {1.76} se mantiene, aunque la tasa de convergencia sea extremadamente lenta o desconocida.

Una diculty con el encuadernado en\ ref {1.75} es que es extremadamente flojo en la mayoría de los casos. Si\(S_{n} / n\) realmente se acercara a\(\bar{X}\) esto lentamente, la débil ley de los grandes números a menudo sería más una curiosidad matemática que un resultado altamente útil. Si asumimos que el MGF de X existe en un intervalo abierto alrededor de 0, entonces\ ref {1.75} puede fortalecerse considerablemente. Recordemos de\ ref {1.64} y\ ref {1.65} que para cualquier\(\epsilon>0\),

\[\operatorname{Pr}\left\{S_{n} / n-\bar{X} \geq \epsilon \quad \leq \exp \left(n \mu_{X}(\bar{X}+\epsilon)\right)\right.\label{1.77} \]

\[\operatorname{Pr}\left\{S_{n} / n-\bar{X} \leq-\epsilon \leq \exp \left(n \mu_{X}(\bar{X}-\epsilon)\right)\right.\label{1.78} \]

donde de Lemma 1.4.1,\(\mu_{X}(a)=\inf _{r}\left\{\gamma_{X}(r)-r a\right\}<0\) para\(a \neq \bar{X}\). Así, para cualquier\(\epsilon>0\),

\[\operatorname{Pr}\left\{\left|S_{n} / n-\bar{X}\right| \geq \epsilon \leq \exp \left[n \mu_{X}(\bar{X}+\epsilon)\right]+\exp \left[n \mu_{X}(\bar{X}-\epsilon)\right]\right.\label{1.79} \]

El límite aquí, para cualquier dado\(\epsilon>0\), disminuye geométricamente en\(n\) lugar de armónicamente. En términos de la Figura 1.11, la altura del rectángulo debe aproximarse a 1 al menos geométricamente en\(n\).

Frecuencia relativa

A continuación mostramos que\ ref {1.76} se puede aplicar a la frecuencia relativa de un evento así como a la media muestral de una variable aleatoria. Supongamos que\(A\) es algún evento en un solo experimento, y que el experimento se repita independientemente\(n\) veces. Entonces, en el modelo de probabilidad para\(n\) las repeticiones, deja\(A_{i}\) ser el evento que\(A\) se da en el\(i \text { th }\) juicio,\(1 \leq i \leq n\). Los eventos\(A_{1}, A_{2}, \ldots, A_{n}\) son entonces IID.

Si dejamos\(\mathbb{I}_{A_{i}}\) ser el indicador rv para A en el\(i \text { th }\) juicio, entonces el rv\(S_{n}=\mathbb{I}_{A_{1}}+\mathbb{I}_{A_{2}}+\cdots+\mathbb{I}_{A_{n}}\) es el número de ocurrencias de\(A\) sobre los\(n\) ensayos. De ello se deduce que

\[\text { relative frequency of } A=\frac{S_{n}}{n}=\frac{\sum_{i=1}^{n} \mathbb{I}_{A_{i}}}{n} \text { . }\label{1.80} \]

Así, la frecuencia relativa de\(A\) es el promedio muestral de los rv binarios\(\mathbb{I}_{A_{i}}\), y todo lo que sabemos sobre la suma de IID rv se aplica igualmente a la frecuencia relativa de un evento. De hecho, todo lo que sabemos sobre las sumas de rv binarios IID se aplica a la frecuencia relativa.

teorema del límite central

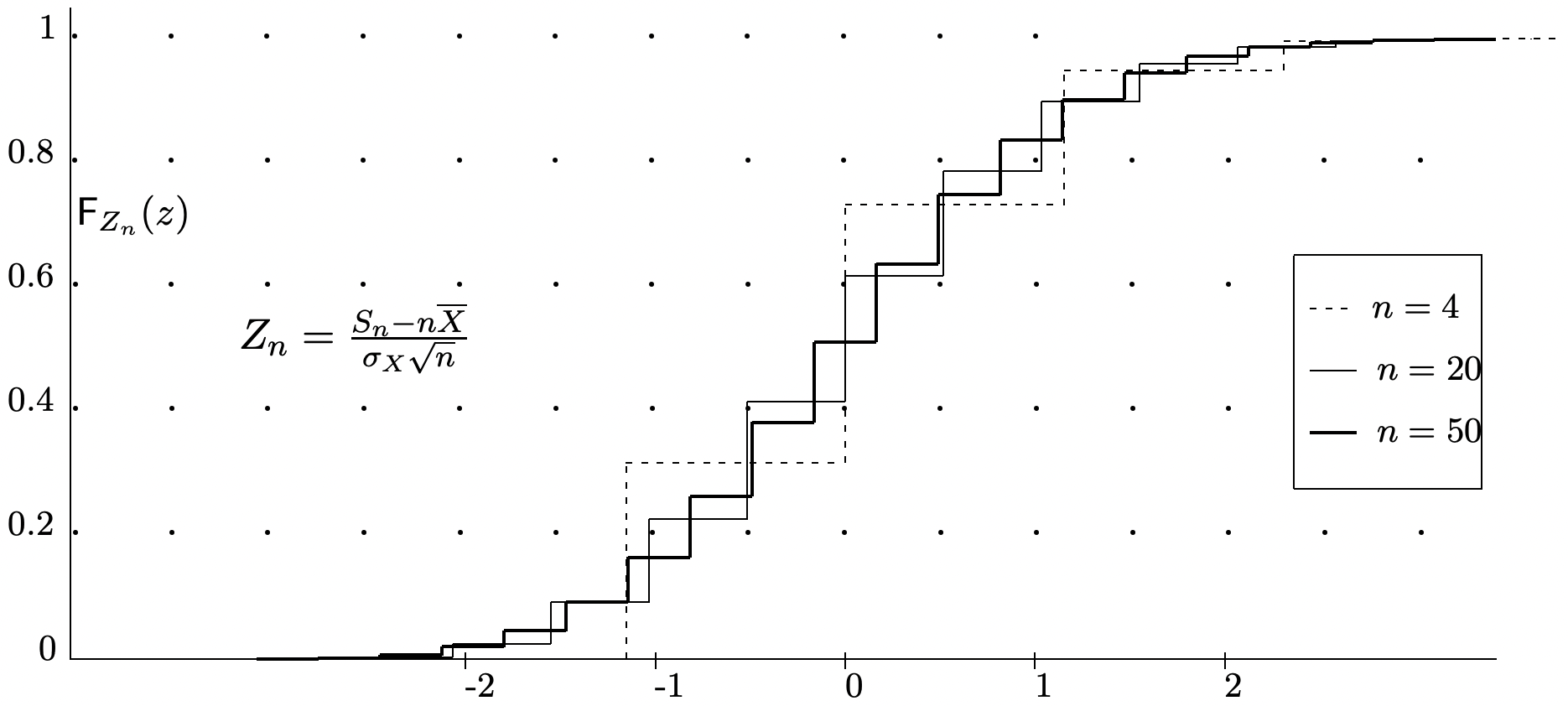
La débil ley de los grandes números dice que con alta probabilidad,\(S_{n} / n\) se acerca a\(\bar{X}\) para grande\(n\), pero establece esto a través de un límite superior en la cola probabilidades más que una estimación de lo que\(\mathrm{F}_{S_{n} / n}\) parece. Si miramos la forma de\(\mathrm{F}_{S_{n} / n}\) para diversos valores de\(n\) en el ejemplo de la Figura 1.10, vemos que la función\(\mathrm{F}_{S_{n} / n}\) se comprime cada vez más a\(\bar{X}\) medida que\(n\) aumenta (de hecho, esta es la esencia de lo que dice la ley débil). Si normalizamos la variable aleatoria\(S_{n} / n\) a 0 media y varianza unitaria, obtenemos una rv normalizada,\(Z_{n}=\left(S_{n} / n-\bar{X}\right) \sqrt{n} / \sigma\). La función de distribución de\(Z_{n}\) se ilustra en la Figura 1.12 para el\(X\) mismo subyacente que se utilizó para\(S_{n} / n\) la Figura 1.10. Las curvas en las dos figuras son las mismas excepto que cada curva ha sido escalada horizontalmente\(\sqrt{n}\) en la Figura 1.12.

La inspección de la Figura 1.12 muestra que las funciones de distribución normalizadas parecen acercarse a una distribución limitante. El teorema del límite central críticamente importante establece que efectivamente existe tal límite, y es la función de distribución gaussiana normalizada.

Figura 1.12: La misma distribución funciona como la Figura 1.5 normalizada a 0 media y desviación estándar unitaria, es decir, las funciones de distribución de\(Z_{n}=\left(S_{n} / n-\bar{X}\right) \frac{\sqrt{n}}{\sigma_{X}}\) para\(n\) =4, 20, 50. Tenga en cuenta que a medida que\(n\) aumenta, la función de distribución de\(Z_{n}\) lentamente comienza a parecerse a la función de distribución normal.

Teorema 1.5.2 (Teorema del límite central (CLT)). \(X_{1}, X_{2}, \ldots\)Sea IID rv con media finita\(\bar{X}\) y varianza finita\(\sigma^{2}\). Entonces por cada número real\(z\),

\[\lim _{n \rightarrow \infty} \operatorname{Pr}\left\{\frac{S_{n}-n \bar{X}}{\sigma \sqrt{n}} \leq z\right\}^{\}}=\Phi(z)\label{1.81} \]

donde\(\Phi(z)\) es la función de distribución normal, es decir, la distribución gaussiana con media 0 y varianza 1,

\(\Phi(z)=\int_{-\infty}^{\}z} \frac{1}{\sqrt{2 \pi}} \exp \left(-\frac{y^{2}}{2}\right) d y\)

Discusión: Los rv\(Z_{n}=\left(S_{n}-n \bar{X}\right) /(\sigma \sqrt{n})\) para cada uno\(n \geq 1\) en el lado izquierdo de\ ref {1.81} cada uno tienen media 0 y varianza 1. El teorema del límite central (CLT), expresado en (1.81), dice que la secuencia de funciones de distribución\(\mathrm{F}_{Z_{1}}(z)\),,\(\mathrm{F}_{Z_{2}}(z), \ldots\) converge en cada valor de\(z\) a\(\Phi(z)\) as\(n \rightarrow \infty\). En otras palabras,\(\lim _{n \rightarrow \infty} \mathrm{F}_{Z_{n}}(z)=\Phi(z)\) para cada uno\(z \in \mathbb{R}\). A esto se le llama convergencia en la distribución, ya que es la secuencia de funciones de distribución, más que la secuencia de rv la que está convergiendo. El teorema se ilustra en la Figura 1.12.

La razón por la que aparece la palabra central en el CLT se puede ver reescribiendo\ ref {1.81} como

\[\lim _{n \rightarrow \infty} \operatorname{Pr}\left\{\frac{S_{n}}{n}-\bar{X} \leq \frac{\sigma z}{\sqrt{n}}\right\}^{\}}=\Phi(z), \label{1.82} \]

Asintóticamente, entonces, estamos viendo una secuencia de promedios muestrales que difieren de la media por una cantidad que va a 0 con\(n\) as\(1 / \sqrt{n}\), es decir, por promedios muestrales muy cercanos a la media para grandes\(n\). Esto debe contrastarse con el límite optimizado de Chernoff en\ ref {1.64} y\ ref {1.65} que observan una secuencia de promedios de muestra que difieren de la media por una cantidad constante para grandes\(n\). Estos últimos resultados son exponencialmente decrecientes\(n\) y se conocen como resultados de gran desviación.

El CLT no dice nada sobre la velocidad de convergencia a la distribución normal. El teorema de BerryesSeen (véase, por ejemplo, Feller, [8]) proporciona alguna orientación sobre esto para los casos en los que\(\left.\mathrm{E}\left[|X-\bar{X}|^{3}\right]\right\}\) existe el tercer momento central. Este teorema afirma que

\[\left|\operatorname{Pr}\left\{\frac{\left.S_{n}-n \bar{X}\right)}{\sigma \sqrt{n}} \leq z\right\}-\Phi(z)\right| \leq \frac{\left.C \mathrm{E}\left[|X-\bar{X}|^{3}\right]\right\}}{\sigma^{3} \sqrt{n}}\label{1.83} \]

donde\(C\) puede estar delimitado por la parte superior por 0.766. Volveremos en breve para discutir la convergencia con mayor detalle.

El CLT ayuda a explicar por qué los rv gaussianos juegan un papel tan central en la teoría de la probabilidad. De hecho, muchas de las fórmulas del libro de cocina de las estadísticas elementales se basan en la suposición tácita de que las variables subyacentes son gaussianas, y el CLT ayuda a explicar por qué estas fórmulas a menudo dan resultados razonables.

Se debe tener cuidado para evitar leer más en el CLT de lo que dice. Por ejemplo, la suma normalizada, no\(\left(S_{n}-n \bar{X}\right) / \sigma \sqrt{n}\) necesita tener una densidad que sea aproximadamente gaussiana. De hecho, si las variables subyacentes son discretas, la suma normalizada es discreta y no tiene densidad. El PMF de la suma normalizada puede tener una estructura fina muy detallada; esto no desaparece a medida que\(n\) aumenta, sino que se “integra” en la función de distribución.

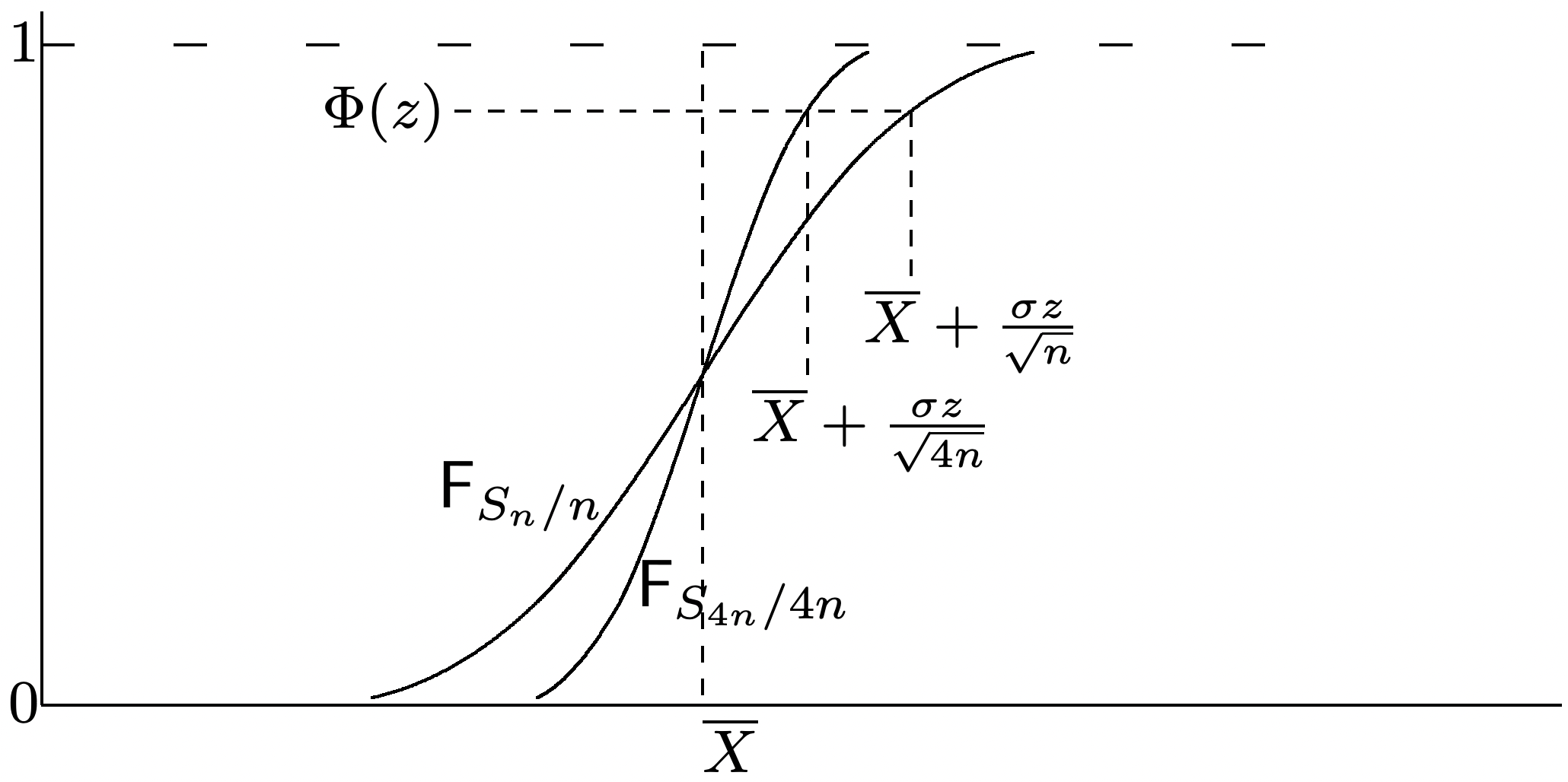
El CLT nos cuenta bastante sobre cómo\(\mathrm{F}_{S_{n} / n}\) converge a una función de paso en\(\bar{X}\). Para ver esto, reescribe\ ref {1.81} en el formulario

\[\lim _{n \rightarrow \infty} \operatorname{Pr}\left\{\frac{S_{n}}{n}-\bar{X} \leq \frac{\sigma z}{\sqrt{n}}\right\}^{\}}=\Phi(z)\label{1.84} \]

Esto se ilustra en la Figura 1.13 donde hemos utilizado\(\Phi(z)\) como aproximación para la probabilidad a la izquierda.

Una prueba del CLT requiere de herramientas matemáticas que no serán necesarias posteriormente. Así damos una prueba sólo para el caso binomial. Feller ([7] y [8]) da una minuciosa y cuidadosa exposición y prueba de varias versiones del CLT incluyendo las de aquí. ³²

Prueba ³³ del Teorema 1.5.2 (caso binomial): Primero establecemos un resultado algo más simple que usa límites finitos en ambos lados de\(\left(S_{n}-n \bar{X}\right) / \sigma \sqrt{n}\), es decir, mostramos que para cualquier finito\(y<z\),

\[\left.\lim _{n \rightarrow \infty} \operatorname{Pr}\left\{y<\frac{S_{n}-n \bar{X}}{\sigma \sqrt{n}} \leq z\right\}^{\}}=\int_{y}^{\}z} \frac{1}{\sqrt{2 \pi}} \exp \left(\frac{-u^{2}}{2}\right)\right\} d u\label{1.85} \]

Figura 1.13: Aproximación de la función de distribución\(\mathrm{F}_{S_{n} / n}\) de un promedio muestral por una distribución gaussiana de la misma media y varianza. Siempre que\(n\) se incremente en un factor de 4, la curva se escala horizontalmente hacia adentro hacia\(\bar{X}\) un factor de 2. El CLT dice tanto que estas curvas se escalan horizontalmente como\(1 / \sqrt{n}\) y también que son mejor aproximadas por el gaussiano de la media dada y varianza a medida que\(n\) aumenta.

La probabilidad a la izquierda de\ ref {1.85} puede ser reescrita como

\ [\ begin {reunió}
\ operatorname {Pr}\ left\ {y<\ frac {S_ {n} -n\ bar {X}} {\ sigma\ sqrt {n}}\ leq z\ derecha\} ^ {\}} =\ nombreoperador {Pr}\ left\ {\ frac {\ sigma y} {\ sqrt {n}} <\ frac {_ {n}} {n} -\ bar {X}\ leq\ frac {\ sigma z} {\ sqrt {n}}\ derecha\} ^ {\}}\\
=\ sum_ {k}\ mathrm {p} _ {S_ {n}} (k)\ texto {para}\ frac { \ sigma y} {\ sqrt {n}} <\ frac {k} {n} -p\ leq\ frac {\ sigma z} {\ sqrt {n}}
\ final {reunidos}\ etiqueta {1.86}\]

Vamos\(\tilde{p}=k / n\),\(\tilde{q}=1-\tilde{p}\), y\(\epsilon(k, n)=\tilde{p}-p\). Abreviamos\(\epsilon(k, n)\) como\(\epsilon\) dónde\(k\) y\(n\) quedan claros a partir del contexto. Desde (1.23), podemos expresarnos\(\mathrm{p}_{S_{n}}(k)\) como

\ [\ begin {alineado}
\ mathrm {p} _ {S_ {n}} (k) &\ sim\ frac {1} {\ sqrt {2\ pi n\ tilde {p}\ tilde {q}}}\ exp n [\ tilde {p}\ ln (p/\ tilde {p}) +\ tilde {q}\ ln (q/\ tilde {q})]\\
&=\ frac {1} {\ sqrt {2\ pi n (p+\ épsilon) (q-\ épsilon)}}\ exp\ izquierda [-n (p+\ épsilon)\ ln\ izquierda (1+\ frac {\ épsilon} {p}\ derecha ) -n (q-\ épsilon)\ ln\ izquierda (1-\ frac {\ épsilon} {q}\ derecha)\ derecha] ^ {\}}\\
&=\ frac {1} {\ sqrt {2\ pi n (p+\ épsilon) (q-\ épsilon)}}\ exp\ izquierda [-n\ izquierda (\ frac {epsilon\ silon^ {2}} {2 p} -\ frac {\ épsilon^ {3}} {6 p^ {2}} +\ cdots+\ frac {\ épsilon^ {2}} {2 q} +\ frac {\ épsilon^ {3}} {6 q^ {2}}\ cdots\ derecho)\ derecho].
\ end {alineado}\ etiqueta {1.87}\]

donde hemos usado la expansión de la serie power,\(\ln (1+u)=u-u^{2} / 2+u^{3} / 3 \cdots\) From (1.86)\(\sigma y / \sqrt{n}<p+\epsilon(k, n) \leq \sigma z / \sqrt{n}\), por lo que los términos omitidos en\ ref {1.87} van a 0 uniformemente sobre el rango de\(k\) in (1.86). El término\((p+\epsilon)(q-\epsilon)\) también converge (uniformemente en\(k\)) a\(pq\) como\(n \rightarrow \infty\). Así

\ [\ begin {alineado}
\ mathrm {p} _ {S_ {n}} (k) &\ sim\ frac {1} {\ sqrt {2\ pi n p q}}\ exp\ izquierda [-n\ izquierda (\ frac {\ épsilon^ {2}} {2 p} +\ frac {\ épsilon^ {2}} {2 q}\ derecha)\ derecha] ^ {\}}\\
&=\ frac {1} {\ sqrt {2\ pi n p q}}\ exp\ izquierda [\ frac {-n\ épsilon^ {2}} {2 p q}\ derecha] ^ {\}}\\
&= frac {1} {\ sqrt {2\ pi n p q}}\ exp\ izquierda [\ frac {-u^ {2} (k, n)} {2}\ derecha] ^ {\}}\ quad\ texto {donde} u (k, n) =\ frac {k-n p} {\ sqrt {p q n}}.
\ end {alineado}\ etiqueta {1.88}\]

Dado que la relación del lado derecho a izquierdo en\ ref {1.88} se acerca a 1\(k\) uniformemente en el rango dado de\(k\),

\[\sum_{k} \mathrm{p}_{S_{n}}(k) \sim \sum\ _{k}^{\}}\frac{1}{\sqrt{2 \pi n p q}} \exp \left[\frac{-u^{2}(k, n)}{2}\right]\label{1.89} \]

Dado que\(u(k, n)\) aumenta en incrementos de\(1 / \sqrt{p q n}\), podemos ver la suma a la derecha arriba como una suma de Riemann aproximándose (1.85). Dado que los términos de la suma se acercan a medida que\(n \rightarrow \infty\), y dado que existe la integral de Riemann,\ ref {1.85} debe cumplirse en el límite.

Para completar la prueba, nota de la desigualdad de Chebyshev que

\(\operatorname{Pr}\left\{\left|S_{n}-\bar{X}\right| \geq \frac{\sigma|y|}{\sqrt{n}}\right\}^{\}} \leq \frac{1}{y^{2}},\)

y por lo tanto

\(\operatorname{Pr}\left\{y<\frac{S_{n}-n \bar{X}}{\sigma \sqrt{n}} \leq z\right\}^{\}} \leq \operatorname{Pr}\left\{\frac{S_{n}-n \bar{X}}{\sigma \sqrt{n}} \leq z\right\}^{\}} \leq \frac{1}{y^{2}}+\operatorname{Pr}\left\{y<\frac{S_{n}-n \bar{X}}{\sigma \sqrt{n}} \leq z\right\}^{\}}\)

Escogiendo\(y=-n^{1 / 4}\), lo vemos\(1 / y^{2} \rightarrow 0\) como\(n \rightarrow \infty\). También\(n \epsilon^{3}(k, n)\) en\ ref {1.87} va a 0 como\(n \rightarrow \infty\) para todos\((k, n)\) satisfactorios\ ref {1.86} con\(y=-n^{1 / 4}\). Tomando el límite como\(n \rightarrow \infty\) entonces prueba el teorema.

Si trazamos a través de las diversas aproximaciones en la prueba anterior, vemos que el error en\(\mathrm{p}_{S_{n}}(k)\) va a 0 as\(1 / n\). Esto es más rápido que el\(1 / \sqrt{n}\) límite en el teorema de Berry-Esseen. Si miramos la Figura 1.3, sin embargo, vemos que la función de distribución de\(S_{n} / n\) contiene pasos de orden\(1 / \sqrt{n}\). Estos pasos verticales hacen que el resultado binomial aquí tenga la misma\(1 / \sqrt{n}\) convergencia lenta que el encuadernado general de Berry-Esseen. Resulta que si evaluamos la función de distribución solo en los puntos medios entre estos pasos, es decir, at\(z=(k+1 / 2-n p) / \sigma \sqrt{n}\), entonces la convergencia en la función de distribución es de orden\(1 / n\).

Dado que el CLT proporciona información tan explícita sobre la convergencia de\(S_{n} / n\) to\(\bar{X}\), es razonable preguntarse por qué es tan importante la débil ley de los grandes números (WLLN). La primera razón es que el WLLN es tan sencillo que puede ser utilizado para dar ideas claras a situaciones en las que el CLT podría confundir el tema. Una segunda razón es que el CLT requiere una varianza, donde como vemos a continuación, el WLLN no. Una tercera razón es que el WLLN puede extenderse a muchas situaciones en las que las variables no son independientes y/o no están distribuidas de manera idéntica. ³⁴ Una razón final es que el WLLN proporciona un límite superior en las colas de\(\mathrm{F}_{S_{n} / n}\), mientras que el CLT proporciona solo una aproximación.

Ley débil con varianza infinita

Ahora establecemos el WLLN sin asumir una varianza finita.

Teorema 1.5.3 (WLLN). Para cada entero\(n \geq 1\), vamos\(S_{n}=X_{1}+\cdots+X_{n}\) donde\(X_{1}, X_{2}, \ldots\) son IID rv satisfactorios\(\mathrm{E}[|X|]<\infty\). Entonces para cualquier\(\epsilon>0\),

\[\lim _{n \rightarrow \infty} \operatorname{Pr}\left\{\left|\frac{S_{n}}{n}-\mathrm{E}[X]\right|>\epsilon\right\}^{\}}=0\label{1.90} \]

Prueba: ³⁵ Utilizamos un argumento de truncamiento; tales argumentos se utilizan frecuentemente para tratar con rv que tienen varianza infinita. La idea subyacente en estos argumentos es importante, pero algunos detalles menos importantes se tratan en el Ejercicio 1.35. Dejar\(b\) ser un número positivo (que luego tomamos para estar aumentando con\(n\)), y para cada variable\(X_{i}\), definir una nueva rv\(\breve{X}_{i}\) (ver Figura 1.14) por

\[\breve{X}_{i}= \begin{cases}X_{i} & \text { for } \quad \mathrm{E}[X]-b \leq X_{i} \leq \mathrm{E}[X]+b \\ \}_{\mathrm{E}}[X]+b & \text { for } \quad X_{i}>\mathrm{E}[X]+b \\ \} \mathrm{E}[X]-b & \text { for } \quad X_{i}<\mathrm{E}[X]-b\end{cases}\label{1.91} \]

Figura 1.14: El rv truncado\(\breve{X}\) para un rv X dado tiene una función de distribución que se trunca en\(\bar{X} \pm b\).

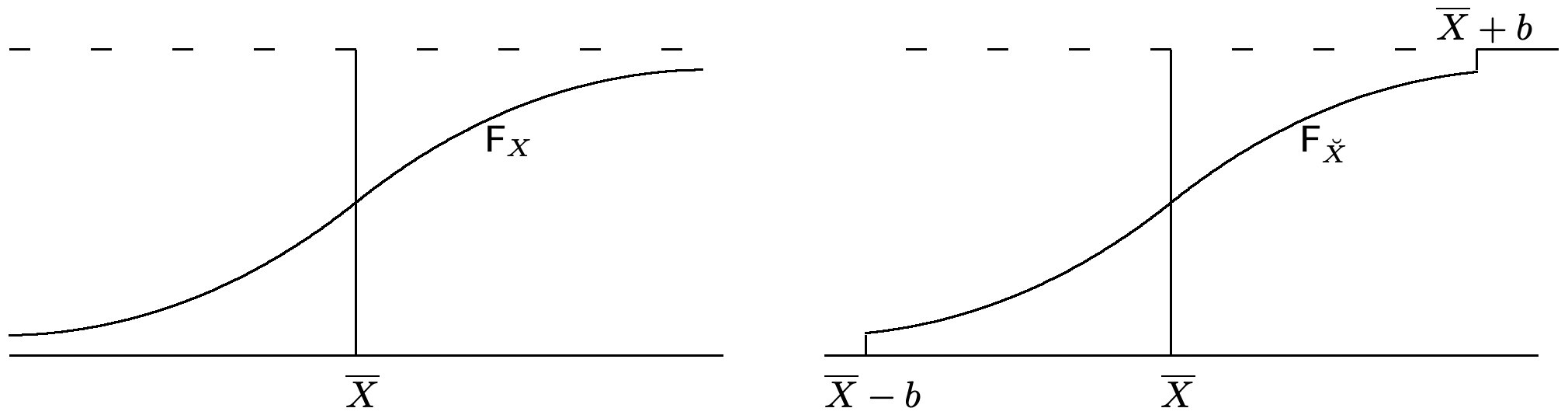
Las variables truncadas\(\breve{X}_{i}\) son IID y, debido al truncamiento, deben tener un segundo momento finito. Así, el WLLN aplica al promedio muestral\(\breve{S}_{n}=\breve{X}_{1}+\cdots \breve{X}_{n}\). Más particularmente, usando la desigualdad Chebshev en forma de\ ref {1.75} on\(\breve{S}_{n} / n\), obtenemos

\(\operatorname{Pr}\left\{\left|\frac{\breve{S}_{n}}{n}-\mathrm{E}[\breve{X}]\right|>\frac{\epsilon}{2}\right\}^{\}} \leq \frac{4 \sigma_{\breve{X}}^{2}}{n \epsilon^{2}} \leq \frac{8 b \mathrm{E}[|X|]}{n \epsilon^{2}}\),

donde el Ejercicio 1.35 demuestra la desigualdad final. El ejercicio 1.35 también muestra que se\(\mathrm{E}[\breve{X}]\}\) acerca\(\mathrm{E}[X]\) como\(b \rightarrow \infty\) y por lo tanto que

\[\operatorname{Pr}\left\{\left|\frac{\breve{S}_{n}}{n}-\mathrm{E}[X]\right|>\epsilon\right\}^{\}} \leq \frac{8 b \mathrm{E}[|X|]}{n \epsilon^{2}},\label{1.92} \]

para todos suciamente grandes\(b\). Este obligado también se aplica\(S_{n} / n\) en el caso donde\(S_{n}=\breve{S}_{n}\), por lo que tenemos el siguiente límite (ver Ejercicio 1.35 para más detalles):

\[\operatorname{Pr}\left\{\left|\frac{S_{n}}{n}-\mathrm{E}[X]\right|>\epsilon\right\}^{\}} \leq \operatorname{Pr}\left\{\left|\frac{\breve{S}_{n}}{n}-\mathrm{E}[X]\right|>\epsilon\right\}+\operatorname{Pr}\left\{S_{n} \neq \breve{S}_{n}\right\}.\label{1.93} \]

La suma original\(S_{n}\) es la misma\(\breve{S}_{n}\) que a menos que uno de los\(X_{i}\) tenga una interrupción, es decir,\(\left|X_{i}-\bar{X}\right|>b\). Así, utilizando la unión ligada,\(\operatorname{Pr}\left\{S_{n} \neq \breve{S}_{n}\right\}^{\}} \leq n \operatorname{Pr}\left\{\left|X_{i}-\bar{X}\right|>b\right.\). Sustituyendo esto y\ ref {1.92} en (1.93),

\[\operatorname{Pr}\left\{\left|\frac{S_{n}}{n}-\mathrm{E}[X]\right|>\epsilon\right\}^{\}}{\leq} \frac{8 b \mathrm{E}[|X|]}{n \epsilon^{2}}+\frac{n}{b}[b \operatorname{Pr}\{|X-\mathrm{E}[X]|>b\}]. \label{1.94} \]

Ahora lo demostramos para cualquier\(\epsilon>0\) y\(\delta>0\),\(\operatorname{Pr}\left\{\left|S_{n} / n-\bar{X}\right| \geq \epsilon \leq \delta\right.\) para todos suciamente grandes\(n\). Esto lo hacemos, por dado\(\epsilon, \delta\), eligiendo\(b(n)\) para cada uno para\(n\) que el primer término en\ ref {1.94} sea igual a\(\delta / 2\). Así\(b(n)=n \delta \epsilon^{2} / 16 \mathrm{E}[|X|]\). Esto quiere decir que\(n / b(n)\) en el segundo término es independiente de\(n\). Ahora desde (1.55),\(\lim _{b \rightarrow \infty} b \operatorname{Pr}\{|X-\bar{X}|>b=0\), así que al elegir\(b(n)\) suciamente grande (y por lo tanto\(n\) suciamente grande), el segundo término en\ ref {1.94} también es como mucho\(\delta / 2\).

Convergencia de variables aleatorias

Esta sección ahora ha desarrollado una serie de resultados sobre cómo la secuencia de promedios de muestra,\(\left\{S_{n} / n ; n \geq 1\right\}\) para una secuencia de IID rv se\(\left\{X_{i} ; i \geq 1\right\}\) aproximan a la media\(\bar{X}\). En el caso del CLT, también se especifica que la distribución limitante alrededor de la media es gaussiana. En el nivel intuitivo más exterior, es decir, en el nivel más útil cuando se mira por primera vez algún conjunto de problemas muy complicado, es muy apropiado ver el límite de los promedios de la muestra como esencialmente igual a la media.

En el siguiente nivel intuitivo hacia abajo, el significado de la palabra se vuelve esencialmente importante y por lo tanto involucra los detalles de las leyes anteriores. Todos los resultados involucran cómo los rv\(S_{n} / n\) cambian\(n\) y se vuelven cada vez más aproximados por\(\bar{X}\). Cuando hablamos de una secuencia de rv (es decir, una secuencia de funciones en el espacio muestral) que se aproxima por una rv o constante numérica, estamos hablando de algún tipo de convergencia, pero claramente no es tan simple como una secuencia de números reales (como\(1 / n\) por ejemplo) convergiendo a algunos dados número (0 por ejemplo).

El propósito de esta sección, es dar nombres y definiciones a estas diversas formas de convergencia. Esto nos dará una mayor comprensión de las leyes de grandes números ya desarrolladas, pero, igualmente importante, nos permitirá desarrollar otra ley de grandes números llamada la ley fuerte de los números grandes (SLLN). Finalmente, nos pondrá en condiciones de utilizar estos resultados de convergencia más tarde para secuencias de rv distintas de los promedios de muestra de IID rv.

Se discuten cuatro tipos de convergencia en lo que sigue, convergencia en distribución, en probabilidad, en cuadrado medio y con probabilidad 1. Para los tres primeros, primero recordamos el tipo de resultado de gran número con ese tipo de convergencia y luego damos la definición general.

Para convergencia con probabilidad 1 (WP1), primero definimos este tipo de convergencia y luego proporcionamos alguna comprensión de lo que significa. Esto se utilizará entonces en el Capítulo 4 para declarar y acreditar el SLLN.

Comenzamos con el teorema del límite central, que, a partir de\ ref {1.81} dice

\(\lim _{n \rightarrow \infty} \operatorname{Pr}\left\{\frac{S_{n}-n \bar{X}}{\sqrt{n} \sigma} \leq z\right\}^{\}}=\int_{-\infty}^{\}z} \frac{1}{\sqrt{2 \pi}} \exp \left(\frac{-x^{2}}{2}\right)^{\}} d x \quad \text { for every } z \in \mathbb{R}\)

Esto se ilustra en la Figura 1.12 y dice que la secuencia (in\(n\)) de funciones de distribución\(\operatorname{Pr}\left\{\frac{S_{n}-n \bar{X}}{\sqrt{n} \sigma} \leq z\right\}^{\}}\) converge en cada una\(z\) a la función de distribución normal at\(z\). Este es un ejemplo de convergencia en la distribución.

Definición 1.5.1. Una secuencia de variables aleatorias,\(Z_{1}, Z_{2}, \ldots\) converge en distribución a una variable aleatoria\(Z\) si\(\lim _{n \rightarrow \infty} \mathrm{F}_{Z_{n}}(z)=\mathrm{F}_{Z}(z)\) en cada una\(z\) para la cual\(\mathrm{F}_{Z}(z)\) es continua.

Para el ejemplo de CLT, las rv que convergen en distribución son\(\left\{\frac{S_{n}-n \bar{X}}{\sqrt{n} \sigma} ; n \geq 1\right\}\), y n convergen en distribución a la rv gaussiana normal.

Convergencia en la distribución no dice que los propios rv convergen en algún sentido razonable, sino sólo que convergen sus funciones de distribución. Por ejemplo, let\(Y_{1}, Y_{2}, \ldots\), ser IID rv, cada uno con la función de distribución\(\mathrm{F}_{Y}\). Para cada uno\(n \geq 1\), si dejamos\(Z_{n}=Y_{n}+1 / n\), entonces es fácil ver que\(\left\{Z_{n} ; n \geq 1\right\}\) converge en distribución a\(Y\). Sin embargo (asumiendo que\(Y\) tiene varianza\(\sigma_{Y}^{2}\) y es independiente de cada uno\(Z_{n}\)), vemos que\(Z_{n}-Y\) tiene varianza\(2 \sigma_{Y}^{2}\). Así\(Z_{n}\) no se acerca\(Y\) como\(n \rightarrow \infty\) en ningún sentido razonable, y\(Z_{n}-Z_{m}\) no llega a ser pequeño como\(n\) y\(m\) ambos se hacen grandes. ³⁶ Como ejemplo aún más trivial, la secuencia\(\left\{Y_{n} n \geq 1\right\}\) converge en distribución a\(Y\).

Para el CLT, son los rv los\(\frac{S_{n}-n \bar{X}}{\sqrt{n} \sigma}\) que convergen en distribución a lo normal. Como se muestra en el Ejercicio 1.38, sin embargo, el rv no\(\frac{S_{n}-n \bar{X}}{\sqrt{n} \sigma}-\frac{S_{2 n}-2 n \bar{X}}{\sqrt{2 n} \sigma}\) está cerca de 0 en ningún sentido razonable, aunque los dos términos tienen funciones de distribución que son muy cercanas para grandes\(n\).

Para el siguiente tipo de convergencia de rv, el WLLN, en forma de (1.90), dice que

\(\lim _{n \rightarrow \infty} \operatorname{Pr}\left\{\left|\frac{S_{n}}{n}-\bar{X}\right|>\epsilon\right\}^{\}}=0 \quad \text { for every } \epsilon>0\)

Este es un ejemplo de convergencia en probabilidad, como se define a continuación:

Definición 1.5.2. Una secuencia de variables aleatorias\(Z_{1}, Z_{2}, \ldots\), converge en probabilidad a un rv\(Z\) si\(\lim _{n \rightarrow \infty} \operatorname{Pr}\left\{\left|Z_{n}-Z\right|>\epsilon\right\}=0\) por cada\(\epsilon>0\).

Para el ejemplo WLLN,\(Z_{n}\) en la definición está la frecuencia relativa\(S _{n} / n\) y\(Z\) es la constante rv\(\bar{X}\). Probablemente sea más simple e intuitivo al pensar en la convergencia de rv pensar en la secuencia de rv\(\left\{Y_{n}=Z_{n}-Z ; n \geq 1\right\}\) como convergente a 0 en algún sentido. ³⁷ Como se ilustra en la Figura 1.10, convergencia en probabilidad significa que\(\left\{Y_{n} ; n \geq 1\right\}\) converge en distribución a una función de paso unitario en 0.

Una declaración equivalente, como se ilustra en la Figura 1.11, es que\(\left\{Y_{n} ; n \geq 1\right\}\) converge en probabilidad a 0 si\(\lim _{n \rightarrow \infty} \mathrm{F}_{Y_{n}}(y)=0\) para todos\(y<0\) y\(\lim _{n \rightarrow \infty} \mathrm{F}_{Y_{n}}(y)=1\) para todos\(y>0\). Esto demuestra que la convergencia en probabilidad es un caso especial de convergencia en distribución, ya que con convergencia en probabilidad, la secuencia\(F_{Y_{n}}\) de funciones de distribución converge a un paso unitario en 0. Tenga en cuenta que no\(\lim _{n \rightarrow \infty} \mathrm{F}_{Y_{n}}(y)\) se especifica en\(y = 0\). Sin embargo, la función de paso no es continua a 0, por lo que no es necesario especificar el límite allí para la convergencia en la distribución.

Convergencia en probabilidad dice bastante más que convergencia en distribución. Como ejemplo importante de esto, considera la diferencia\(Y_{n}-Y_{m}\) para\(n\) y\(m\) ambos grandes. Si\(\{Y_{n} ; n \geq1\}\) converge en probabilidad a 0, entonces\(Y_{n}\) y ambos\(Y_{m}\) están cerca de 0 con alta probabilidad para grandes\(n\) y\(m\), y por lo tanto cerca entre sí. Más precisamente,\(\lim _{m \rightarrow \infty, n \rightarrow \infty} \operatorname{Pr}\left\{\left|Y_{n}-Y_{m}\right|>\epsilon\right\}=0\) para cada\(\epsilon>0\). Si la secuencia\(\left\{Y_{n} ; n \geq 1\right\}\) simplemente converge en distribución a alguna distribución arbitraria, entonces, como vimos,\(Z_{n}-Z_{m}\) puede ser grande con alta probabilidad, incluso cuando\(n\) y\(m\) son grandes. Otro ejemplo de ello se da en el Ejercicio 1.38.

Parece paradójico que el CLT sea más explícito sobre la convergencia de\(S_{n} / n\) a\(\bar{X}\) que la ley débil, pero corresponde a un tipo de convergencia más débil. La resolución de esta paradoja es que la secuencia de rv en el CLT es\(\left\{\frac{S_{n}-n \bar{X}}{\sqrt{n} \sigma} ; n \geq 1\right\}\). La presencia de\(\sqrt{n}\) en el denominador de esta secuencia proporciona información mucho más detallada sobre cómo\(S_{n} / n\) se acerca\(\bar{X}\) con el aumento\(n\) que el paso unitario limitante de\(\mathrm{F}_{S_{n} / n}\) sí mismo. Por ejemplo, es fácil ver desde el CLT eso\(\lim _{n \rightarrow \infty} \mathrm{F}_{S_{n} / n}(\bar{X})=1 / 2\), que no puede derivarse directamente de la ley débil.

Otro tipo de convergencia es la convergencia en el cuadrado medio (MS). Un ejemplo de esto, para el promedio muestral\(S_{n} / n\) de IID rv con varianza, se da en (1.74), repetido a continuación:

\(\lim _{n \rightarrow \infty} \mathrm{E}\left[\left(\frac{S_{n}}{n}-\bar{X}\right)^{2}\right]^{\}}=0\)

La definición general es la siguiente:

Definición 1.5.3. Una secuencia de rv\(Z_{1}, Z_{2}, \ldots\), converge en cuadrado medio (MS) a un rv\(Z\) si\(\left.\lim _{n \rightarrow \infty} \mathrm{E}\left[\left(Z_{n}-Z\right)^{2}\right]\right\}=0\).

Nuestra derivación de la ley débil de los grandes números (Teorema 1.5.1) se basó esencialmente en la convergencia MS de (1.74). Utilizando el mismo enfoque, el Ejercicio 1.37 muestra en general que la convergencia en MS implica convergencia en probabilidad. La convergencia en probabilidad no implica convergencia MS, ya que como se muestra en el Teorema 1.5.3, la ley débil de los grandes números se mantiene sin necesidad de varianza.

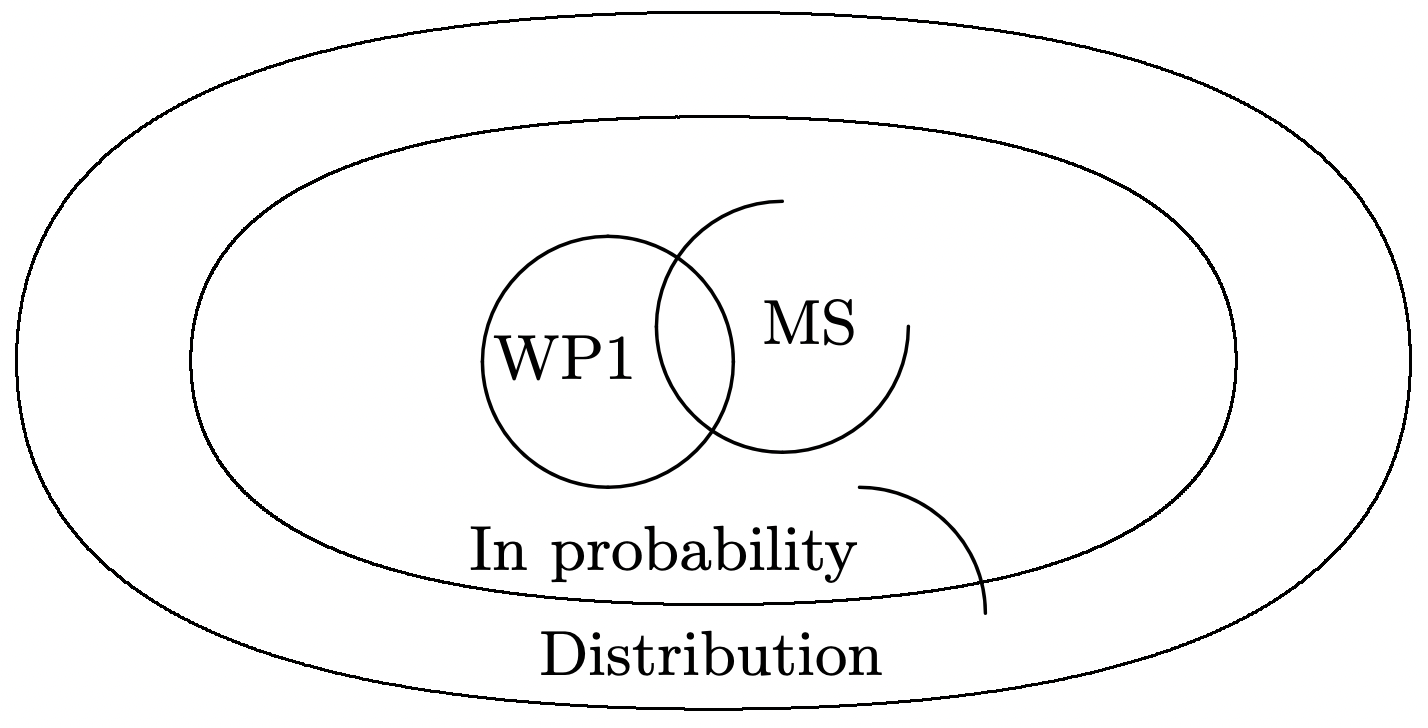
La Figura 1.15 ilustra la relación entre estas formas de convergencia, es decir, la convergencia cuadrática media implica convergencia en probabilidad, lo que a su vez implica convergencia en la distribución. La figura también muestra convergencia con probabilidad 1 (WP1), que es la siguiente forma de convergencia a discutir.

Figura 1.15: Relación entre diferentes tipos de convergencia: La convergencia en la distribución es la más general y está implicada por todas las demás. La convergencia en probabilidad es la siguiente más general y está implicada por la convergencia con probabilidad 1 (WP1) y por la convergencia cuadrática media (MS), ninguna de las cuales implica la otra.

Convergencia con probabilidad 1

A continuación definimos y discutimos la convergencia con probabilidad 1, abreviada como convergencia WP1. Convergencia WP1 a menudo se conoce como convergencia a.s. (casi seguramente) y convergencia a.e. (casi en todas partes). La fuerte ley de los grandes números, que se discute brevemente en esta sección y se discute más y se prueba en diversas formas en los Capítulos 4 y 7, proporciona un ejemplo sumamente importante de convergencia WP1. La definición general es la siguiente:

Definición 1.5.4. Dejar\(Z_{1}, Z_{2}, \ldots\), ser una secuencia de rv en un espacio de muestra\(\Omega\) y dejar\(Z\) ser otro rv en\(\Omega\). Luego\(\left\{Z_{n} ; n \geq 1\right\}\) se define para converger\(Z\) con probabilidad 1 (WP1) si

\[\operatorname{Pr}\left\{\omega \in \Omega: \lim _{n \rightarrow \infty} Z_{n}(\omega)=Z(\omega)\right\}^{\}}=1\label{1.95} \]

La condición a menudo\(\operatorname{Pr}\left\{\omega \in \Omega: \lim _{n \rightarrow \infty} Z_{n}(\omega)=Z(\omega)\right\}=1\) se afirma de manera más compacta como\(\operatorname{Pr}\left\{\lim _{n} Z_{n}=Z\right\}=1\), y aún más compacta como\(\lim _{n} Z_{n}=Z\) WP1, pero la forma aquí es la más simple para la comprensión inicial. Como se discute en el Capítulo 4. el SLLN dice que si\(\left\{X_{i} ; i \geq 1\right\}\) son IID con\(\mathrm{E}[|X|]<\infty\), entonces la secuencia de promedios muestrales,\(\left\{S_{n} / n ; n \geq 1\right\}\) converge WP1 a\(\bar{X}\).

Al tratar de entender (1.95), tenga en cuenta que cada punto\(\omega\) de muestreo del espacio muestral subyacente se\(\Omega\) mapea a un valor\(Z_{n}(\omega)\) de muestra de cada rv\(Z_{n}\), y así se mapea a una ruta de muestreo\(\left\{Z_{n}(\omega) ; n \geq 1\right\}\). Para cualquier dado\(\omega\), tal ruta de muestra es simplemente una secuencia de números reales. Esa secuencia de números reales podría converger a\(Z(\omega)\) (que es un número real para lo dado\(\omega\)), podría converger a otra cosa, o podría no converger en absoluto. Así, existe un conjunto de\(\omega\) para el que\(\left\{Z_{n}(\omega) ; n \geq 1\right\}\) converge la ruta de muestreo correspondiente\(Z(\omega)\), y un segundo conjunto para el que la ruta de muestreo converge a otra cosa o no converge en absoluto. La convergencia WP1 de la secuencia de rv se define así para que ocurra cuando el primer conjunto de rutas de muestra anterior tiene probabilidad 1.

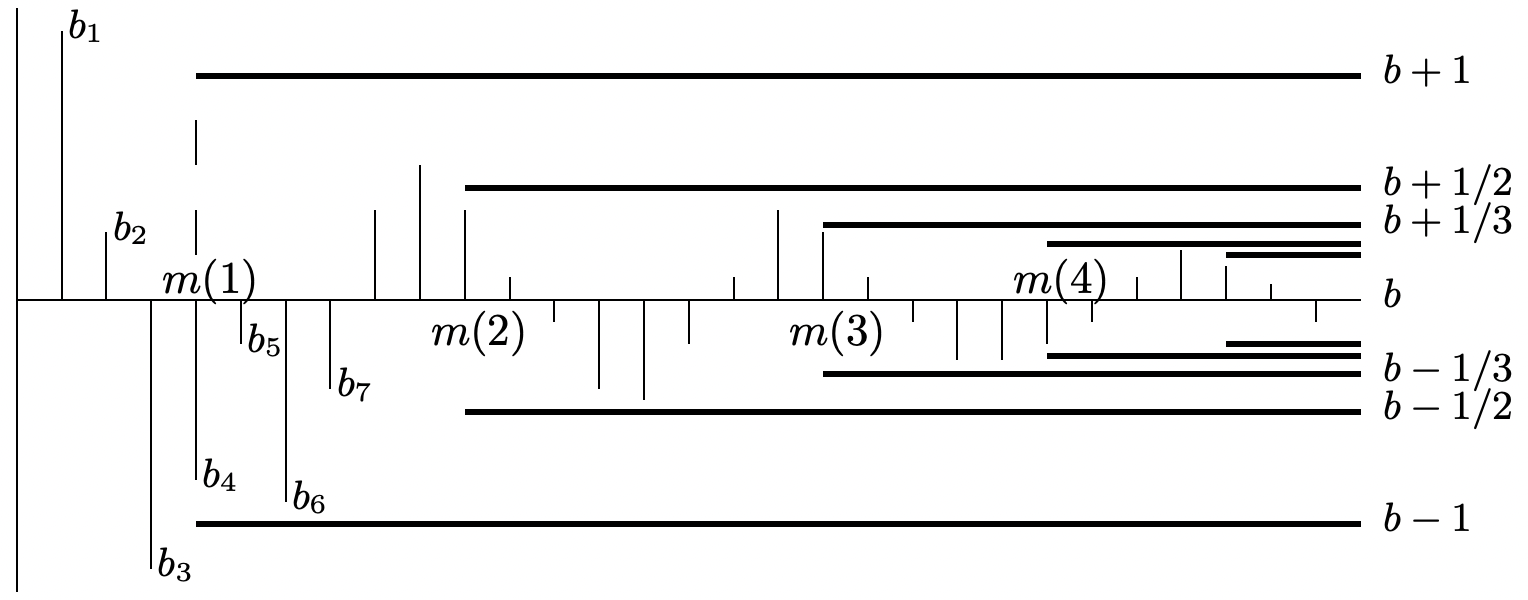
Para cada uno\(\omega\), la secuencia\(\left\{Z_{n}(\omega) ; n \geq 1\right\}\) es simplemente una secuencia de números reales, por lo que revisamos brevemente cuál es el límite de tal secuencia. Una secuencia de números reales\(b_{1}, b_{2}\)... se dice que tiene un límite\(b\) si, por cada\(\epsilon>0\), hay un entero\(m_{\epsilon}\) tal que\(\left|b_{n}-b\right| \leq \epsilon\) para todos\(n \geq m_{\epsilon}\). Una sentencia equivalente es que\(b_{1}, b_{2}, \ldots\), tiene un límite\(b\) si, por cada entero\(k \geq 1\), hay un entero\(m(k)\) tal que\(\left|b_{n}-b\right| \leq 1 / k\) para todos\(n \geq m(k)\).

La figura 1.16 ilustra esta definición para aquellos, como el autor, cuyos ojos se difuminan en el segundo o tercer 'existe allí', 'tal que', etc. en un enunciado. Como se ilustra, un aspecto importante de la convergencia de una secuencia\(\left\{b_{n} ; n \geq 1\right\}\) de números reales es que\(b_{n}\) se acerca a\(b\) para grandes\(n\) y se mantiene cerca para todos los valores suciamente grandes de\(n\).

Figura 1.16: Ilustración de una secuencia de números reales\(b_{1}, b_{2}, \ldots\) que convergen a un número\(b\). La figura ilustra un entero\(m(1)\) tal que para todos\(n \geq m(1), b_{n}\) se encuentra en el intervalo\(b \pm 1\). Del mismo modo, para cada uno\(k \geq 1\), hay un entero\(m(k)\) tal que\(b_{n}\) yace en\(b \pm 1 / k\) para todos\(n \geq m(k)\). Por lo tanto,\(\lim _{n \rightarrow \infty} b_{n}=b\) significa que para una secuencia de restricciones cada vez más estrictas, la restricción késima se puede cumplir para todos los sucientemente grandes\(n\), (es decir, todos\(n \geq m(k))\). Intuitivamente, la convergencia significa que los elementos\(b_{1}, b_{2}, \ldots\) se acercan\(b\) y se mantienen cerca. La secuencia de enteros positivos\(m(1), m(2), \ldots\) es no decreciente, pero por lo demás arbitraria, dependiendo únicamente de la secuencia\(\left\{b_{n} ; n \geq 1\right\}\). Para las secuencias que convergen muy lentamente, los números enteros\(m(1), m(2), \ldots\) son simplemente correspondientemente más grandes.

La Figura 1.17 da un ejemplo de una secuencia de números reales que no converge. Intuitivamente, esta secuencia es cercana a 0 (y de hecho idénticamente igual a 0) para la mayoría de las grandes\(n\), pero no se mantiene cerca

Figura 1.17: Ilustración de una secuencia no convergente de números reales\(b_{1}, b_{2}, \ldots\) La secuencia se define por\(b_{n}=3 / 4\)\(n=1,5,25, \ldots, 5^{j}, \ldots\) para todos los enteros\(j \geq 0\). Para todos los demás\(n, b_{n}=0\). Los términos para los cuales\(b_{n} \neq 0\) se vuelven cada vez más raros como\(n \rightarrow \infty\). Tenga en cuenta que\(b_{n} \in[1,1]\) para todos\(n\), pero no hay\(m(2)\) tal que\(b_{n} \in\left[-\frac{1}{2}, \frac{1}{2}\right]\) para todos\(n \geq m(2)\). Así la secuencia no converge.

El siguiente ejemplo ilustra cómo una secuencia de rv puede converger en probabilidad pero no converger WP1. El ejemplo también proporciona algunas pistas sobre por qué la convergencia WP1 es importante.

Ejemplo 1.5.1. Consideremos una secuencia\(\left\{Z_{n} ; n \geq 1\right\}\) de rv para la cual las trayectorias muestrales constituyen la siguiente ligera variación de la secuencia de números reales en la Figura 1.17. En particular, como se ilustra en la Figura 1.18, el término distinto de cero\(n=5^{j}\) en la Figura 1.17 se sustituye por un término distinto de cero\(n\) en un intervalo elegido aleatoriamente\(\left[5^{j}, 5^{j+1}\right)\).

Figura 1.18: Ilustración de una ruta muestral de una secuencia de rv\(\left\{Y_{n} ; n \geq 0\right\}\) donde, para cada una\(j \geq 0, Y_{n}=1\) para una elección equiprobable de\(n \in\left[5^{j}, 5^{j+1}\right)\) y de\(Y_{n}=0\) otra manera.

Dado que cada ruta de muestra contiene una sola en cada segmento\(\left[5^{j}, 5^{j+1}\right)\) y contiene cero en otra parte, ninguna de las rutas de muestra converge. En otras palabras,\(\operatorname{Pr}\left\{\omega: \lim Z_{n}(\omega)=0\right\}=0\) más que 1. Por otro lado\(\operatorname{Pr}\left\{Z_{n}=0\right\}=1-5^{-j}\) para\(5^{j} \leq n<5^{j+1}\), así\(\lim _{n \rightarrow \infty} \operatorname{Pr}\left\{Z_{n}=0\right\}=1\).

Así esta secuencia de rv converge a 0 en probabilidad, pero no converge a 0 WP1. Esta secuencia también converge en cuadrado medio y (ya que converge en probabilidad) en distribución. Así hemos demostrado (con el ejemplo) que la convergencia WP1 no está implicada por ninguno de los otros tipos de convergencia que hemos discutido. Mostraremos en la Sección 4.2 que la convergencia WP1 implica convergencia en probabilidad y en distribución pero no en el cuadrado medio (como se ilustra en la Figura 1.15).

El punto interesante de este ejemplo es que esta secuencia de rv no es extraña (aunque es algo especializada para hacer sencillo el análisis). Otro punto importante es que esta definición de convergencia tiene una larga historia de ser aceptada como la forma 'útil', 'natural' y 'correcta' de definir la convergencia para una secuencia de números reales. Por lo tanto, no es sorprendente que la convergencia WP1 resulte igualmente útil para secuencias de rv.

Hay un precio a pagar al usar el concepto de convergencia WP1. Luego debemos mirar toda la secuencia de rv y ya no podemos analizar\(n\) -tuplas finitas y luego ir al límite como\(n \rightarrow \infty\). Esto requiere una capa adicional significativa de abstracción, lo que implica una precisión matemática adicional y una pérdida inicial de intuición. Por esta razón pospusimos más discusión sobre la convergencia WP1 y el SLLN hasta el Capítulo 4 donde se necesita.

---

Referencia

³¹ Decir esto en palabras le da a uno un mayor respeto por la notación matemática, y tal vez en este caso, es preferible simplemente entender la afirmación matemática (1.76).

³² Muchos textos elementales proporcionan 'pruebas simples', utilizando técnicas de transformación, pero, entre otros problemas, suelen indicar que la suma normalizada tiene una densidad que se aproxima a la densidad gaussiana, que es incorrecta para todas las rv discretas.

³³ Esta prueba puede omitirse sin pérdida de continuidad. Sin embargo, es una parte importante para lograr una comprensión profunda del CLT.

³⁴ Los teoremas del límite central también se mantienen en muchas de estas situaciones más generales, pero no sostienen tan ampliamente como el WLLN.

³⁵ Los detalles de esta prueba pueden omitirse sin pérdida de continuidad. No obstante, se debe entender la estructura general del argumento de truncamiento.

³⁶ De hecho, decir que una secuencia de rv converge en distribución es una terminología lamentable pero estándar. Sería igual de conciso, y mucho menos confuso, decir que una secuencia de funciones de distribución convergen en lugar de decir que una secuencia de rv convergen en distribución.

³⁷ Definición 1.5.2 da la impresión de que la convergencia a una rv\(Z\) es más general que la convergencia a una constante o la convergencia a 0, pero convertir las rv a\(Y_{n}=Z_{n}-Z\) deja claro que esta generalidad añadida es bastante superficial.