2.4: Procesos Poisson no homogéneos
- Page ID
- 86203
El proceso de Poisson, tal y como lo definimos, se caracteriza por una tasa de llegada constante\(\lambda\). A menudo es útil considerar un tipo de proceso más general en el que la tasa de llegada varía en función del tiempo. Un proceso de Poisson no homogéneo con tasa de llegada variable en el tiempo\(\lambda(t)\) se define 9 como un proceso de conteo\(\{N(t) ; t>0\}\) que tiene la propiedad de incremento independiente y\(t \geq 0\), para todos\(\delta>0\), también satisface:
\ [\ begin {alineado}
&\ nombreoperador {Pr}\ {\ tilde {N} (t, t+\ delta) =0\} ^\} =1-\ delta\ lambda (t) +o (\ delta)\\
&\ nombreoperador {Pr}\ {\ tilde ancho {N} (t, t+\ delta) =1\} ^\} =\ delta\ lambda (t) +o (\ delta)\\
&\ nombreoperador {Pr}\ {\ Widetilde {N} (t, t+\ delta)\ geq 2\} ^\} =o (\ delta)
\ end {alineado}\ etiqueta {2.29}\]
donde\(\tilde{N}(t, t+\delta)=N(t+\delta)-N(t)\). El proceso de Poisson no homogéneo no tiene la propiedad de incremento estacionario.
Una aplicación común ocurre en la comunicación óptica donde a menudo se usa un proceso de Poisson no homogéneo para modelar la corriente de fotones de un modulador óptico; la modulación se logra variando la intensidad del fotón\(\lambda(t)\). Veremos en breve otra aplicación en el siguiente ejemplo. A veces un proceso de Poisson, como lo definimos anteriormente, se llama proceso de Poisson homogéneo.
Podemos utilizar de nuevo un “proceso de Bernoulli que se encoge” para aproximar un proceso de Poisson no homogéneo. Para ver cómo hacer esto, supongamos que\(\lambda(t)\) está acotado lejos de cero. Particionamos el eje de tiempo en incrementos cuyas longitudes\(\delta\) varían inversamente\(\lambda(t)\), manteniendo así la probabilidad de una llegada en un incremento en algún valor fijo\(p=\delta \lambda(t)\). Así, ignorando temporalmente la variación de\(\lambda(t)\) dentro de un incremento,
\ [\ begin {aligned}
&\ operatorname {Pr}\ left\ {\ tilde {N}\ left (t, t+\ frac {p} {\ lambda (t)}\ right) ^\} =0\ derecha\} ^\} =1-p+o (p)\\
&\ operatorname {Pr}\ left\ {\ Widetilde {N}\ left (t, t+\ frac {p} {\ lambda (t)}\ derecha) ^\} =1\ derecha\} ^\} =p+o (p)\\
&\ nombreoperador {Pr}\ izquierda\ {\ Widetilde {N}\ izquierda (t, t+\ frac {p} {\ lambda (t)}\ derecha) ^ {\}}\ geq 2\ derecha\} ^\} =o (\ épsilon)
\ final {alineado}\ etiqueta {2.30}\]
Esta partición se define con mayor precisión definiendo\(m(t)\) como
\[m(t)=\int_{0}^{\}t} \lambda(\tau) d \tau\label{2.31} \]
Entonces el incremento\(i\) th termina en aquello\(t\) para el cual\(m(t) = i p\).
Como antes, dejemos\(\left\{Y_{i} ; i \geq 1\right\}\) ser una secuencia de rv binarios IID con\(\operatorname{Pr}\left\{Y_{i}=1\right\}=p\) y\(\operatorname{Pr}\left\{Y_{i}=0\right\}=1-p\). Considera el proceso de conteo\(\{N(t) ; t>0\}\) en el que\(Y_{i}\), para cada uno\(i \geq 1\), denota el número de llegadas en el intervalo\(\left(t_{i-1}, t_{i}\right]\), donde\(t_{i}\) satisface\(m\left(t_{i}\right)=i p\). Así,\(N\left(t_{i}\right)=Y_{1}+Y_{2}+\cdots+Y_{i}\). Si\(p\) se disminuye como\(2^{-j}\), cada incremento se divide sucesivamente en un par de incrementos. Así, por el mismo argumento que en (2.22),
\[\operatorname{Pr}\{N(t)=n\}=\frac{[1+o(p)][m(t)]^{n} \exp [-m(t)]}{n !}\label{2.32} \]
Del mismo modo, para cualquier intervalo\((t, \tau]\)\(\tilde{m}_{\}}(t, \tau)=\int_{t}^{\tau} \lambda(u) d u\), tomando, y tomando\(t=t_{k}\),\(\tau=t_{i}\) para algunos\(k\)\(i\),, obtenemos
\[\operatorname{Pr}\{\tilde{N}(t, \tau)=n\}^\}=\frac{[1+o(p)]\left[\widetilde{m}_{\}}{(t, \tau)}\right]^{n} \exp \left[-\widetilde{m}_{\}}(t, \tau)\right]}{n !}\label{2.33} \]
Yendo al límite\(p \rightarrow 0\), el proceso de conteo\(\{N(t) ; t>0\}\) anterior se acerca al proceso no homogéneo de Poisson bajo consideración, y tenemos el siguiente teorema:
Para un proceso de Poisson no homogéneo con tasa de llegada continua derecha\(\lambda(t)\) limitada lejos de cero, la distribución de\(\tilde{N}(t, \tau)\), el número de llegadas en\((t, \tau]\), satisface
\[\operatorname{Pr}\{\widetilde{N}(t, \tau)=n\}^\}=\frac{[\widetilde{m}_\}(t, \tau)]^{n} \exp [-\widetilde{m}(t, \tau)]}{n !}\label{2.34} \]
donde\[\widetilde{m}_{\}}(t, \tau)=\int_{t}^{\}\tau} \lambda(u) d u \label{2.34B} \]
Por lo tanto, se puede ver un proceso de Poisson no homogéneo como un proceso de Poisson (homogéneo) en una escala de tiempo no lineal. Es decir, dejar\(\left\{N^{*}(s) ; s \geq 0\right\}\) ser un proceso de Poisson (homogéneo) con tasa 1. El proceso de Poisson no homogéneo es entonces dado por\(N(t)=N^{*}(m(t))\) para cada uno\(t\).
Usando la notación de cola explicada en el Ejemplo 2.3.1, una\(M / G / \infty\) cola indica una cola con llegadas de Poisson, una distribución de servicios generales y un número infinito de servidores. Dado que la\(\mathrm{M} / \mathrm{G} / \infty\) cola tiene un número infinito de servidores, nunca se pone en cola a los clientes que llegan. Cada llegada inmediatamente comienza a ser atendida por algún servidor, y el tiempo\(Y_{i}\) de servicio del cliente\(i\) es IID terminado\(i\) con alguna función de distribución dada\(G(y)\); el tiempo de servicio es el intervalo desde el inicio hasta la finalización del servicio y también es independiente de las épocas de llegada. Nos gustaría encontrar la función de distribución del número de clientes atendidos en una época determinada\(\tau\).
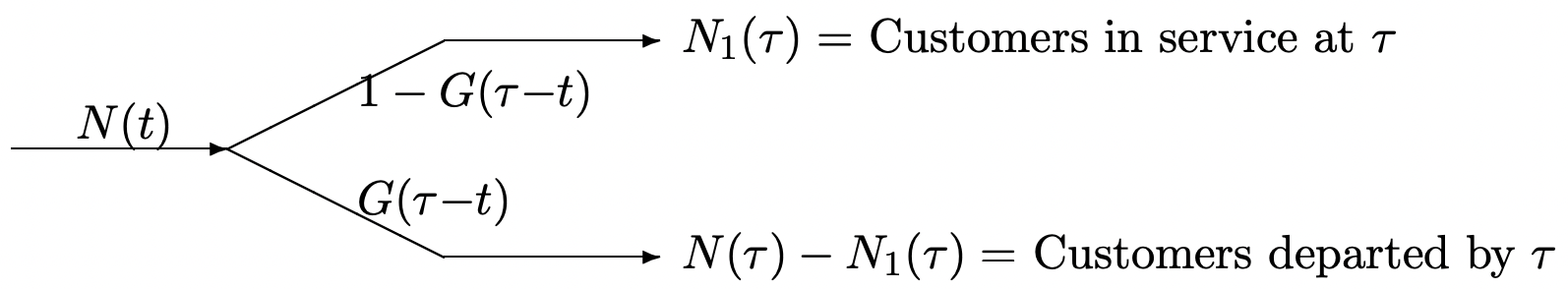
\(\{N(t) ; t>0\}\)Sea el proceso de conteo de Poisson, a razón\(\lambda\), de llegadas de clientes. Considera los horarios de llegada de aquellos clientes que aún están en servicio en algún momento fijo\(\mathcal{T}\). En algún intervalo arbitrariamente pequeño\((t, t+\delta]\), la probabilidad de una llegada es\(\delta \lambda+o(\delta)\) y la probabilidad de 2 o más llegadas es despreciable (es decir,\(o(\delta)\)). La probabilidad de que un cliente llegue\((t, t+\delta]\) y siga siendo atendido a tiempo\(\tau>t\) es entonces\(\delta \lambda[1-G(\tau-t)]+o(\delta)\). Considere un proceso de conteo\(\left\{N_{1}(t) ; 0<t \leq \tau\right\}\) donde\(N_{1}(t)\) está el número de llegadas entre 0 y\(t\) que aún están en servicio en\(\mathcal{T}\). Este proceso de conteo tiene la propiedad de incremento independiente. Para ver esto, tenga en cuenta que las llegadas generales en\(\{N(t) ; t>0\}\) tienen la propiedad de incremento independiente; también las llegadas en\(\{N(t) ; t>0\}\) tienen tiempos de servicio independientes, y por lo tanto son independientes en o no en\(\left\{N_{1}(t) ; 0<t \leq \tau\right\}\). De ello se deduce que\(\left\{N_{1}(t) ; 0<t \leq \tau\right\}\) es un proceso de Poisson no homogéneo con tasa\(\lambda[1-G(\tau-t)]\) en el tiempo\(t \leq \tau\). El número esperado de llegadas que aún están en servicio a la hora\(\mathcal{T}\) es entonces
\[m(\tau)=\lambda \int_{t=0}^{\}\tau}[1-G(\tau-t)] d t=\lambda \int_{t=0}^{\}\tau}[1-G(t)] d t\label{2.35} \]
y el PMF del número en servicio en el momento\(\mathcal{T}\) es dado por
\[\operatorname{Pr}\left\{N_{1}(\tau)=n\right\}=\frac{m(\tau)^{n} \exp (-m(\tau))}{n !}\label{2.36} \]
Obsérvese que como\(\tau \rightarrow \infty\), la integral en\ ref {2.35} se acerca a la media de la distribución del tiempo de servicio (es decir, es la integral de la función de distribución complementaria\(1-G(t)\),, del tiempo de servicio). Esto significa que en estado estacionario (as\(\tau \rightarrow \infty\)), la distribución del número en servicio\(\tau\) depende de la distribución del tiempo de servicio solo a través de su media. Este ejemplo se puede utilizar para modelar situaciones como el número de llamadas telefónicas que tienen lugar en una época determinada. Esto requiere que las llegadas de nuevas llamadas se modelen como un proceso de Poisson y que el tiempo de espera de cada llamada se modele como una variable aleatoria independiente de otros tiempos de espera y de los tiempos de llegada de llamadas. Finalmente, como se muestra en la Figura 2.8, podemos considerar\(\left\{N_{1}(t) ; 0<t \leq \tau\right\}\) como una división del proceso de llegada\(\{N(t) ; t>0\}\). Por el mismo tipo de argumento que en la Sección 2.3, el número de clientes que han completado el servicio por tiempo\(\tau\) es independiente del número que aún está en servicio.
9 Suponemos que\(\lambda(t)\) es correcto continuo, es decir, que para cada uno\(t\),\(\lambda(t)\) es el límite de\(\lambda(t+\epsilon)\) como se\(\epsilon\) acerca a 0 desde arriba. Esto\(\lambda(t)\) permite contener discontinuidades, como se ilustra en la Figura 2.7, pero sigue la convención de que el valor de la función en la discontinuidad es el valor limitante desde la derecha. Esta convención se requiere en\ ref {2.29} para hablar de la distribución de llegadas justo a la derecha del tiempo\(t\).