3.6: Teoría de la Decisión de Markov y Programación Dinámica

En el apartado anterior, analizamos el comportamiento de una cadena de Markov con recompensas. En esta sección, consideramos una estructura mucho más elaborada en la que un tomador de decisiones puede elegir entre diversas recompensas posibles y probabilidades de transición. En lugar de la recompensa\(r_{i}\) y las probabilidades de transición\(\left\{P_{i j} ; 1 \leq j \leq \mathrm{M}\right\}\) asociadas a un estado dado\(i\), hay una opción entre cierto número\(K_{i}\) de recompensas diferentes, digamos\(r_{i}^{(1)}, r_{i}^{(2)}, \ldots, r_{i}^{\left(K_{i}\right)}\) y una elección correspondiente entre\(K_{i}\) diferentes conjuntos de probabilidades de transición, digamos \(\left\{P_{i j}^{(1)} ; 1 \leq j \leq \mathrm{M}\right\},\left\{P_{i j}^{(2)}, 1 \leq j\leq\mathrm{M}\right\},\dots\left\{ P_{ij}^{(K_i)};1\leq j\leq \mathrm{M}\right\}\). En cada momento\(m\), un tomador de decisiones, dado\(X_{m}=i\), selecciona ij una de las\(K_{i}\) posibles opciones para el estado\(i\). Obsérvese que si la decisión\(k\) se elige en estado\(i\), entonces la recompensa es\(r_{i}^{(k)}\) y las probabilidades de transición de\(i\) son\(\left\{P_{i j}^{(k)} ; 1 \leq j \leq \mathrm{M}\right\}\); no es permisible elegir\(r_{i}^{(k)}\) por uno\(k\) y\(\left\{P_{i j}^{(k)} ; 1 \leq j \leq \mathrm{M}\right\}\) para otro\(k\). También asumimos que si\(k\) se selecciona la decisión en el momento\(m\), la probabilidad de ingresar al estado\(j\) en el momento\(m+1\) es\(P_{i j}^{(k)}\), independiente de estados y decisiones anteriores.

La figura 3.9 muestra un ejemplo de esta situación en la que el tomador de decisiones puede elegir entre dos posibles decisiones en el estado 2\(\left(K_{2}=2\right)\), y no tiene libertad de elección en el estado 1\(\left(K_{1}=1\right)\). Esta figura ilustra el equilibrio familiar entre la gratificación instantánea (alternativa 2) y la gratificación a largo plazo (alternativa 1).

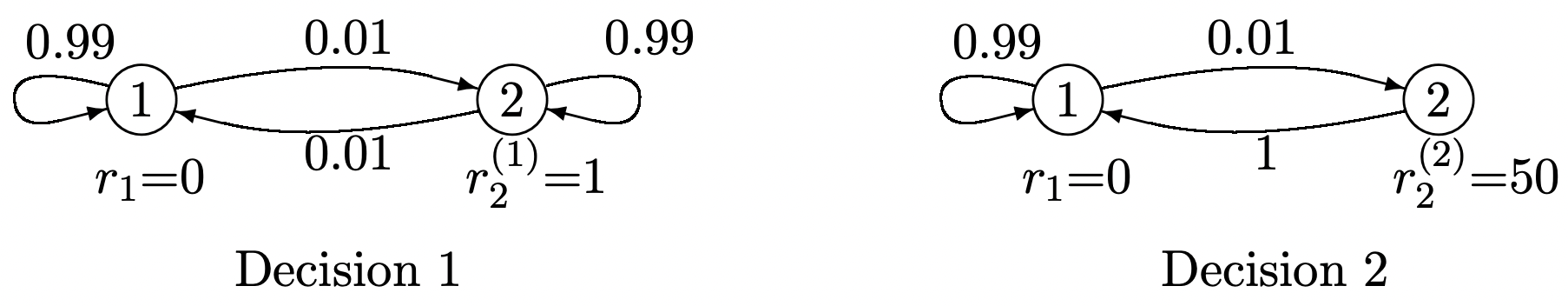Figura 3.9: Un problema de decisión de Markov con dos alternativas en el estado 2.

El conjunto de reglas que utiliza el tomador de decisiones para seleccionar una alternativa en cada momento se denomina política. Queremos considerar la recompensa agregada esperada sobre\(n\) los escalones de la “cadena Markov” en función de la política utilizada por el tomador de decisiones. Si para cada estado\(i\), la política utiliza la misma decisión, digamos\(k_{i}\), en cada ocurrencia de\(i\), entonces esa política corresponde a una cadena homogénea de Markov con probabilidades de transición\(P_{i j}^{\left(k_{i}\right)}\). Denotamos la matriz de estas probabilidades de transición como\(\left[P^{k}\right]\), dónde\(\boldsymbol{k}=\left(k_{1}, \ldots, k_{\mathrm{M}}\right)\). Tal política, es decir, mapear cada estado\(i\) en una decisión fija\(k_{i}\), independiente del tiempo y del pasado, se denomina política estacionaria. La ganancia agregada para cualquier política estacionaria de este tipo se encontró en el apartado anterior. Dado que tanto las recompensas como las probabilidades de transición dependen únicamente del estado y de la decisión correspondiente, y no a tiempo, uno siente intuitivamente que las políticas estacionarias tienen cierto sentido a lo largo de un largo período de tiempo. Por otro lado, si nos fijamos en el ejemplo de la Figura 3.9, es claro que la decisión 2 es la mejor opción en el estado 2 al\(n\) th de\(n\) los ensayos, pero es menos obvio qué hacer en juicios anteriores.

En lo que sigue, primero derivamos la política óptima para maximizar la recompensa agregada esperada sobre un número arbitrario\(n\) de juicios, digamos a veces\(m\) a\(m+n-1\). Veremos que la decisión en su momento\(m+h\),\(0 \leq h<n\), para la política óptima de hecho puede depender de\(h\) y\(n\) (pero no\(m\)). Resulta simplificar las cosas considerablemente si incluimos una recompensa final\(\left\{u_{i} ; 1 \leq i \leq \mathrm{M}\right\}\) en su momento\(m+n\). Esta recompensa final\(\boldsymbol{u}\) se considera como un vector fijo, para ser elegido según corresponda, y no como parte de la elección de la política.

Esta estrategia optimizada, en función del número de pasos n y la recompensa final\(\boldsymbol{u}\), se denomina una política dinámica óptima para eso\(\boldsymbol{u}\). Esta política se encuentra a partir del algoritmo de programación dinámica, que, como veremos, es conceptualmente muy simple. Luego vamos a encontrar la relación entre las políticas dinámicas óptimas y las políticas estacionarias óptimas. Encontraremos que, en condiciones bastante generales, cada uno tiene la misma ganancia a largo plazo por juicio.

Algoritmo Dinámico

Al igual que en nuestro desarrollo de las cadenas de Markov con recompensas, consideramos la recompensa agregada esperada\(m\) a lo largo de periodos de\(n\) tiempo, digamos\(m+n-1\), con una recompensa final a la vez\(m+n\). Primero considere la decisión óptima con\(n=1\). Dado\(X_{m}=i\),\(k\) se toma una decisión con recompensa inmediata\(r_{i}^{(k)}\). Con probabilidad\(P_{i j}^{(k)}\) el siguiente estado\(X_{m+1}\) es estado\(j\) y la recompensa final es entonces\(u_{j}\). La recompensa agregada esperada a lo largo de\(m\) los tiempos y\(m+1\), maximizada sobre la decisión\(k\), es entonces

\[v_{i}^{*}(1, \boldsymbol{u})=\max _{k}\left\{r_{i}^{(k)}+\sum_{j} P_{i j}^{(k)} u_{j}\right\}\label{3.42} \]

Siendo explícito acerca de la decisión maximizadora\(k^{\prime}\),\ ref {3.42} se convierte

\ [\ begin {reunió}
v_ {i} ^ {*} (1,\ negridsymbol {u}) =r_ {i} ^ {\ left (k^ {\ prime}\ derecha)} +\ sum_ {j} P_ {i j} ^ {\ left (k^ {\ prime}\ derecha)} u_ {j}\ quad\ text {for} k^ {prime\}\ text {tal que}\\
r_ {i} ^ {\ izquierda (k^ {\ prime}\ derecha)} +\ suma_ {j} P_ {i j} ^ {\ izquierda (k^ {\ prime}\ derecha)} u_ {j} =\ max _ {k}\ izquierda\ {r_ {i } ^ {(k)} +\ suma_ {j} P_ {i j} ^ {(k)} u_ {j}\ derecha\}
\ fin {reunidos}\ etiqueta {3.43}\]

Tenga en cuenta que una decisión se toma sólo a tiempo\(m\), pero que hay dos recompensas, una a la vez\(m\) y la otra, la recompensa final, a la vez\(m+1\). Usamos la notación\(v_{i}^{*}(n, \boldsymbol{u})\) para representar la recompensa agregada máxima esperada desde tiempos\(m\) hasta\(m+n\) comenzar en\(X_{m}=i\). Las decisiones (con el vector de recompensa\(\boldsymbol{r}\)) se toman en los\(n\) momentos\(m\) a\(m+n-1\), y esto es seguido por un vector de recompensa final\(\boldsymbol{u}\) (sin ninguna decisión) en el momento\(m+n\). A menudo simplifica la notación para definir el vector de recompensas agregadas máximas esperadas

\(\boldsymbol{v}^{*}(n, \boldsymbol{u})=\left(v_{1}^{*}(n, \boldsymbol{u}), v_{2}^{*}(n, \boldsymbol{u}), \ldots, v_{\mathrm{M}}^{*}(1, \boldsymbol{u})\right)^{\top}\).

Con esta notación,\ ref {3.42} y\ ref {3.43} se convierten

\[\boldsymbol{v}^{*}(1, \boldsymbol{u})=\max _{\boldsymbol{k}}\left\{\boldsymbol{r}^{k}+\left[P^{\boldsymbol{k}}\right] \boldsymbol{u}\right\} \quad \text { where } \boldsymbol{k}=\left(k_{1}, \ldots, k_{\mathrm{M}}\right)^{\top}, \boldsymbol{r}^{\boldsymbol{k}}=\left(r_{1}^{k_{1}}, \ldots, r_{\mathrm{M}}^{k_{\mathrm{M}}}\right)^{\top}. \label{3.44} \]

\[\boldsymbol{v}^{*}(1, \boldsymbol{u})=\boldsymbol{r}^{k^{\prime}}+\left[P^{k^{\prime}}\right] \boldsymbol{u} \quad \text { where } \boldsymbol{r}^{k^{\prime}}+\left[P^{k^{\prime}}\right] \boldsymbol{u}=\max _{\boldsymbol{k}} \boldsymbol{r}^{k}+\left[P^{k}\right] \boldsymbol{u} .\label{3.45} \]

Ahora considere\(v_{i}^{*}(2, \boldsymbol{u})\), es decir, la recompensa agregada máxima esperada a partir de\(X_{m}=i\) las decisiones tomadas a veces\(m\)\(m+1\) y una recompensa final a la vez\(m+2\). La clave de la programación dinámica es que una decisión óptima en el momento se\(m+1\) puede seleccionar basándose únicamente en el estado\(j\) en el momento\(m+1\); esta decisión (dada\(X_{m+1}=j\)) es óptima independiente de la decisión en el momento\(m\). Es decir, sea cual sea la decisión que se tome en su momento\(m\), la recompensa máxima esperada a veces\(m+1\) y\(m+2\), dada\(X_{m+1}=j\), es\(\max _{k}\left(r_{j}^{(k)}+\sum_{\ell} P_{j \ell}^{(k)} u_{\ell}\right)\). Obsérvese que este máximo es\(v_{j}^{*}(1, \boldsymbol{u})\), como se encuentra en (3.42).

Utilizando esta decisión optimizada en el momento\(m+1\), se ve que si\(X_{m}=i\) y la decisión\(k\) se toma en el momento\(m\), entonces la suma de recompensas esperadas a veces\(m+1\) y\(m+2\) es\(\sum_{j} P_{i j}^{(k)} v_{j}^{*}(1, \boldsymbol{u})\). Añadiendo la recompensa esperada en el momento\(m\) y maximizando sobre las decisiones en el momento\(m\),

\[v_{i}^{*}(2, \boldsymbol{u})=\max _{k}\left(r_{i}^{(k)}+\sum_{j} P_{i j}^{(k)} v_{j}^{*}(1, \boldsymbol{u})\right)\label{3.46} \]

En otras palabras, la ganancia agregada máxima\(m\) a lo largo de los tiempos hasta\(m+2\) (usando la recompensa\(\boldsymbol{u}\) final en\(m+2\)) es la máxima sobre las opciones en el momento\(m\) de la suma de la recompensa en\(m\) más la recompensa agregada máxima esperada para\(m+1\) y\(m+2\). La simple expresión de\ ref {3.46} resulta del hecho de que la maximización sobre la elección en el tiempo\(m+1\) depende del estado en\(m+1\) pero, dado ese estado, es independiente de la política elegida en el momento\(m\).

Este mismo argumento se puede utilizar para todos los números mayores de ensayos. Para encontrar la recompensa agregada máxima esperada de vez\(m\) en cuando\(m+n\), primero encontramos la recompensa agregada máxima esperada de\(m+1\) a\(m+n\), condicional\(X_{m+1}=j\) para cada estado\(j\). Esto es lo mismo que la recompensa agregada máxima esperada de vez\(m\) en cuando\(m+n-1\), que es\(v_{j}^{*}(n-1, \boldsymbol{u})\). Esto nos da la expresión general de\(n \geq 2\),

\[v_{i}^{*}(n, \boldsymbol{u})=\max _{k}\left(r_{i}^{(k)}+\sum_{j} P_{i j}^{(k)} v_{j}^{*}(n-1, \boldsymbol{u})\right)\label{3.47} \]

También podemos escribir esto en forma de vector como

\[\boldsymbol{v}^{*}(n, \boldsymbol{u})=\max _{\boldsymbol{k}}\left(\boldsymbol{r}^{\boldsymbol{k}}+\left[P^{\boldsymbol{k}}\right] \boldsymbol{v}^{*}(n-1, \boldsymbol{u})\right)\label{3.48} \]

Aquí\(\boldsymbol{k}\) hay un conjunto (o vector) de decisiones,\(\boldsymbol{k}=\left(k_{1}, k_{2}, \ldots, k_{\mathrm{M}}\right)^{\top}\), donde\(k_{i}\) está la decisión para el estado\(i\). \(\left[P^{\boldsymbol{k}}\right]\)denota una matriz cuyo\((i, j)\) elemento es\(P_{i j}^{\left(k_{i}\right)}\), y\(\boldsymbol{r}^{\boldsymbol{k}}\) denota un vector cuyo elemento\(i\) th es\(r_{i}^{\left(k_{i}\right)}\). La maximización sobre\(\boldsymbol{k}\) en\ ref {3.48} es realmente M maximizaciones separadas e independientes, una para cada estado, es decir,\ ref {3.48} es simplemente una forma vectorial de (3.47). Otra forma frecuentemente útil de reescribir\ ref {3.48} es la siguiente:

\ [\ begin {array} {c}\ boldsymbol {v} ^ {*} (n,\ negridsymbol {u}) =\ negridsymbol {r} ^ {\ negridsymbol {k} ^ {\ prime}} +\ left [P^ {\ negritas {k} ^ {\ prime}}\ derecha]\ negridsymbol {v} ^ {*} (n-1,\ boldsymbol {u})\ quad\ text {for}\ boldsymbol {k} ^ {\ prime}\ texto {tal que}\\
\ negrilla {r} ^ {\ negridsymbol {k} ^ {\ prime}} +\ left [P^ {\ boldsymbol {k} ^ {\ prime}}\ derecha]\ negridsymbol {v} ^ {*} (n-1,\ negridsymbol {u}) =\ max _ {\ negridsymbol {k}}\ left (\ boldsymbol {r} ^ {\ boldsymbol {k}} +\ left [P^ {\ boldsymbol {k}}\ right]\ negridsymbol {k} v} ^ {*} (n-1,\ negridsymbol {u})\ derecha)
\ end {array}\ label {3.49}\]

Si\(\boldsymbol{k}^{\prime}\) satisface (3.49), entonces\(\boldsymbol{k}^{\prime}\) es una decisión óptima en un momento arbitrario\(m\) dado, primero, que el objetivo es maximizar la ganancia agregada de tiempo\(m\) a\(m+n\), segundo, que las decisiones óptimas para este objetivo se van a tomar\(m+1\) a veces para\(m+n-1\), y, tercero, ese\(\boldsymbol{u}\) es el vector de recompensa final en\(m+n\). De la misma manera,\(\boldsymbol{v}^{*}(n, \boldsymbol{u})\) es la recompensa máxima esperada sobre esta secuencia finita de\(n\) decisiones desde\(m\) hasta\(m+n-1\) con la recompensa final\(\boldsymbol{u}\) en\(m+n\).

Tenga en cuenta que (3.47), (3.48) y\ ref {3.49} son válidos sin restricciones (como estados recurrentes o aperiódicos) sobre las posibles probabilidades de transición\(\left[P^{\boldsymbol{k}}\right]\). Estas ecuaciones también son válidas en principio si el tamaño del espacio estatal es infinito. Sin embargo, la optimización para cada uno\(n\) puede entonces depender de un número infinito de optimizaciones en\(n-1\), lo que a menudo es inviable.

El algoritmo de programación dinámica es solo el cálculo de (3.47), (3.48), o (3.49), realizado iterativamente para\(n=1,2,3, \ldots\) El desarrollo de este algoritmo, como herramienta sistemática para resolver esta clase de problemas, se debe a Bellman [Bel57]. Tenga en cuenta que el algoritmo es independiente de la hora de inicio\(m\); el parámetro\(n\), generalmente denominado etapa\(n\), es el número de decisiones sobre las cuales se está optimizando la ganancia agregada. Este algoritmo produce la política dinámica óptima para cualquier vector de recompensa final fijo\(\boldsymbol{u}\) y cualquier número dado de ensayos. Junto con el cálculo de\(\boldsymbol{v}^{*}(n, \boldsymbol{u})\) para cada uno\(n\), el algoritmo también arroja la decisión óptima en cada etapa (bajo el supuesto de que se va a utilizar la política óptima para cada etapa numerada inferior, es decir, para cada prueba posterior del proceso).

La sorprendente simplicidad del algoritmo se debe a la propiedad Markov. Es decir,\(v_{i}^{*}(n, \boldsymbol{u})\) es la recompensa agregada presente y futura condicionada al estado presente. Al estar condicionado al estado presente, es independiente del pasado (es decir, cómo el proceso llegó al estado i de transiciones y elecciones anteriores).

Aunque la programación dinámica es computacionalmente sencilla y conveniente ¹³, el comportamiento asintótico de no\(\boldsymbol{v}^{*}(n, \boldsymbol{u}) as \(n \rightarrow \infty\) es evidente a partir del algoritmo. Después de elaborar algunos ejemplos simples, nos fijamos en la cuestión general del comportamiento asintótico.

Ejemplo 3.6.1

Considera la Figura 3.9, repetida a continuación, con las recompensas finales\(u_{2}=u_{1}=0\).

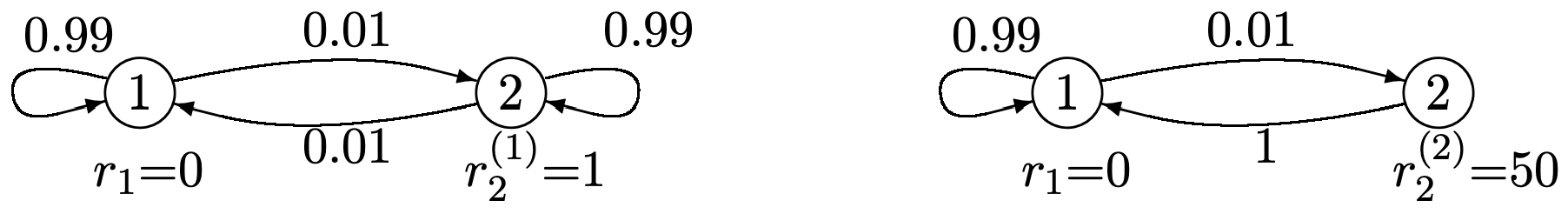
Solución

Desde\(r_{1}=0\) y\(u_{1}=u_{2}=0\), la ganancia agregada en el estado 1 en la etapa 1 es

\(v_{1}^{*}(1, \boldsymbol{u})=r_{1}+\sum_{j} P_{1 j} u_{j}=0\)

De igual manera, dado que la póliza 1 tiene una recompensa inmediata\(r_{2}^{(1)}=1\) en el estado 2, y la póliza 2 tiene una recompensa inmediata\(r_{2}^{(2)}=50\),

\(v_{2}^{*}(1, \boldsymbol{u})=\max \left\{\left[r_{2}^{(1)}+\sum_{j} P_{2 j}^{(1)} u_{j}\right], \quad\left[r_{2}^{(2)}+\sum_{j} P_{2 j}^{(2)} u_{j}\right]\right\}=\max \{1,50\}=50\)

Ahora podemos pasar a la etapa 2, utilizando los resultados anteriores para\(v_{j}^{*}(1, \boldsymbol{u})\). Desde (3.46),

\ (\ begin {alineado}
v_ {1} ^ {*} (2,\ negridsymbol {u}) &=r_ {1} +P_ {11} v_ {1} ^ {*} (1,\ negritas {u}) +P_ {12} v_ {2} ^ {*} (1,\ negridsymbol {u}) =P_ {12} v_ {2} ^ {*} (1,\ negridsymbol {u}) =0.5\\
v_ {2} ^ {*} (2,\ negridsymbol {u}) &=\ max\ izquierda\ {\ izquierda [r_ {2} ^ {(1)} +\ sum_ {j} P_ {2 j} ^ {(1)} v_ {j} ^ {*} (1,\ boldsymbol {u})\ derecha],\ quad\ izquierda [r_ {2} ^ {(2)} +P_ {21} ^ {(2)} v_ {1} ^ {*} (1,\ negritas {u})\ derecha]\ derecha\}\\
&=\ max\ izquierda\ {\ izquierda [1+P_ {22} ^ {(1)} v_ {2} ^ {*} (1,\ negridsymbol {u})\ derecha], 50\ derecha\} =\ max\ {50.5,50\} =50.5
\ end {alineado}\)

Así, para dos juicios, la decisión 1 es óptima en el estado 2 para el primer juicio (etapa 2), y la decisión 2 es óptima en el estado 2 para el segundo juicio (etapa 1). Lo que está sucediendo es que la elección de la decisión 2 en la etapa 1 ha hecho muy rentable estar en el estado 2 en la etapa 1. Así, si la cadena está en el estado 2 en la etapa 2, es preferible elegir la decisión 1 (es decir, la ganancia de unidad pequeña) en la etapa 2 con la alta probabilidad correspondiente de permanecer en el estado 2 en la etapa 1. Continuando con este cómputo para mayores\(n\), uno encuentra que\(v_{1}^{*}(n, \boldsymbol{u})=n / 2\) y\(v_{2}^{*}(n, \boldsymbol{u})=50+n / 2\). La política dinámica óptima (para\(\boldsymbol{u}=0\)) es la decisión 2 para la etapa 1 (es decir, para la última decisión a tomar) y la decisión 1 para todas las etapas\(n>1\) (es decir, para todas las decisiones anteriores a la última).

Este ejemplo también ilustra que la maximización de la ganancia esperada no es necesariamente lo que es más deseable en todas las aplicaciones. Por ejemplo, las personas con aversión al riesgo bien podrían preferir la decisión 2 en la siguiente decisión final (etapa 2). Esto garantiza una recompensa de 50, en lugar de tener una pequeña oportunidad de perder esa recompensa.

Ejemplo 3.6.2 (Problemas de la ruta más corta)

El problema de encontrar las rutas más cortas entre nodos en una gráfica dirigida surge en muchas situaciones, desde el enrutamiento en redes de comunicación hasta el cálculo del tiempo para completar tareas complejas. El problema es bastante similar al tiempo esperado de primer paso del ejemplo 3.5.1. En ese problema, los arcos en una gráfica dirigida se seleccionaron de acuerdo con una distribución de probabilidad, mientras que aquí se deben tomar decisiones sobre qué arcos tomar. Aunque esto no es un problema probabilístico, las decisiones pueden plantearse como elegir un arco dado con probabilidad uno, viendo así el problema como un caso especial de programación dinámica.

Solución

Considera encontrar la ruta más corta desde cada nodo en una gráfica dirigida a algún nodo en particular, digamos el nodo 1 (ver Figura 3.10). Cada arco (excepto el arco especial (1, 1)) tiene asociada una longitud de enlace positiva que podría reflejar la distancia física o un tipo de costo arbitrario. El arco especial (1, 1) tiene 0 longitud de enlace. La longitud de un camino es la suma de las longitudes de los arcos en ese camino. En términos de programación dinámica, una política es una elección de arco fuera de cada nodo (estado). Aquí queremos minimizar el costo (es decir, la longitud de la ruta) en lugar de maximizar la recompensa, por lo que simplemente reemplazamos el máximo en el algoritmo de programación dinámica por un mínimo (o, si se desea, todos los costos pueden ser reemplazados por recompensas negativas).

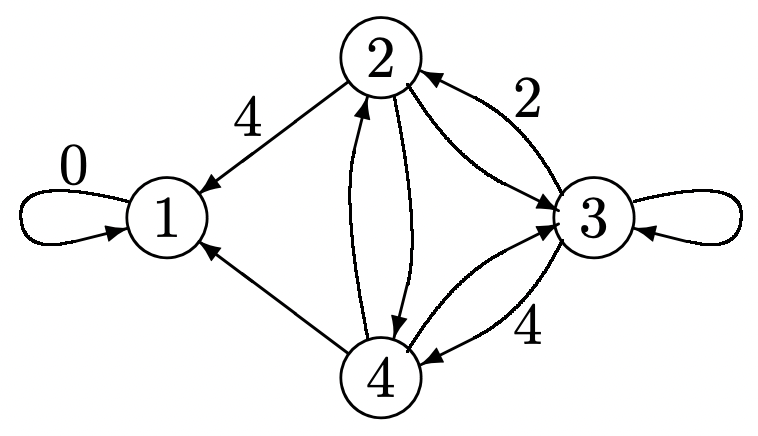Figura 3.10: Un problema de ruta más corta. Los arcos están marcados con sus longitudes. Los arcos sin marcar tienen longitud unitaria.

Iniciamos el algoritmo de programación dinámica con un vector de costo final que es 0 para el nodo 1 e infinito para todos los demás nodos. En la etapa 1, la decisión de costo mínimo para el nodo (estado) 2 es arco (2, 1) con un costo igual a 4. La decisión de costo mínimo para el nodo 4 es (4, 1) con costo unitario. El costo del nodo 3 (en la etapa 1) es infinito cualquiera que sea la decisión que se tome. Los costos de la etapa 1 son entonces

\(v_{1}^{*}(1, \boldsymbol{u})=0, \quad v_{2}^{*}(1, \boldsymbol{u})=4, \quad v_{3}^{*}(1, \boldsymbol{u})=\infty, \quad v_{4}^{*}(1, \boldsymbol{u})=1\)

En la etapa 2, el costo\(v_{3}^{*}(2, \boldsymbol{u})\), por ejemplo, es

\(v_{3}^{*}(2, \boldsymbol{u})=\min \left[2+v_{2}^{*}(1, \boldsymbol{u}), \quad 4+v_{4}^{*}(1, \boldsymbol{u})\right]=5\)

El conjunto de costos en la etapa 2 son

\(v_{1}^{*}(2, \boldsymbol{u})=0, \quad v_{2}^{*}(2, \boldsymbol{u})=2, \quad v_{3}^{*}(2, \boldsymbol{u})=5, \quad v_{4}^{*}(2, \boldsymbol{u})=1\)

La decisión en la etapa 2 es que el nodo 2 vaya al 4, el nodo 3 al 4 y el 4 al 1. En la etapa 3, el nodo 3 cambia al nodo 2, reduciendo su longitud de ruta a 4, y los nodos 2 y 4 no cambian. Las iteraciones adicionales no producen ningún cambio, y la política resultante también es la política estacionaria óptima.

Los resultados anteriores en cada etapa\(n\) pueden interpretarse como los caminos más cortos restringidos a como máximo\(n\) saltos. A medida\(n\) que se incrementa, esta restricción se relaja sucesivamente, alcanzando los verdaderos caminos más cortos en menos de M etapas.

Se puede ver sin demasiada dificultad que estos costos agregados finales (longitudes de ruta) también resultan sin importar qué vector de costo final\(\boldsymbol{u}\) (con\(u_{1}=0\)) se utilice. Esta es una característica útil para muchos tipos de redes donde las longitudes de los enlaces cambian muy lentamente con el tiempo y se desea un algoritmo de ruta más corta que pueda rastrear los cambios correspondientes en las rutas más cortas.

Políticas estacionarias óptimas

En el Ejemplo 3.6.1, vimos que hubo un transitorio final (en la etapa 1) en el que se tomó la decisión 1, y en todas las demás etapas, se tomó la decisión 2. Así, la política dinámica óptima consistió en una política estacionaria a largo plazo, seguida de un periodo transitorio (para una sola etapa en este caso) sobre el cual se utilizó una política diferente. Resulta que este transitorio final se puede evitar eligiendo un vector de recompensa final apropiado\(\boldsymbol{u}\) para el algoritmo de programación dinámica. Si se tiene muy buena intuición, se podría adivinar que la elección apropiada de la recompensa final\(\boldsymbol{u}\) es el vector de ganancia relativa\(\boldsymbol{w}\) asociado a la política óptima a largo plazo.

Parece razonable esperar este mismo tipo de comportamiento para problemas típicos pero más complejos de decisión de Markov. Para entender esto, comenzamos por considerar una política estacionaria arbitraria\(\boldsymbol{k}^{\prime}=\left(k_{1}^{\prime}, \ldots, k_{\mathrm{M}}^{\prime}\right)\) y denotar la matriz de transición de la cadena asociada de Markov como\(\left[P^{\boldsymbol{k^{\prime}}}\right]\). Suponemos que asoció a la cadena de Markov es una unicaína, o, abbrevando terminología, que\(\boldsymbol{k}^{\prime}\) es una unicaína. Let\(\boldsymbol{w}^{\prime}\) Ser el único vector de ganancia relativa-para\(\boldsymbol{k}^{\prime}\). Luego encontramos algunas condiciones necesarias\(\boldsymbol{k}^{\prime}\) para ser la política dinámica óptima en cada etapa usando\(\boldsymbol{w}^{\prime}\) como vector de recompensa final.

Primero, de\ ref {3.45}\(\boldsymbol{k}^{\prime}\) es una decisión dinámica óptima (con el vector de recompensa final\(\boldsymbol{w}^{\prime}\) para\(\left[P^{\boldsymbol{k^{\prime}}}\right]\)) en la etapa 1 si

\[\boldsymbol{r^{k^{\prime}}}+\left[\boldsymbol{P^{k^{\prime}}}\right] \boldsymbol{w}^{\prime}=\max _{\boldsymbol{k}}\left\{\boldsymbol{r^{k}}+\left[\boldsymbol{P^{k}}\right] \boldsymbol{w}^{\prime}\right\}\label{3.50} \]

Tenga en cuenta que esto es más que una simple afirmación que se\(\boldsymbol{k}^{\prime}\) puede encontrar maximizando\(\boldsymbol{r^k}+\left[P^{ \boldsymbol{k}}\right] \boldsymbol{w}^{\prime}\) sobre\(\boldsymbol{k}\). También implica el hecho de que\(\boldsymbol{w}^{\prime}\) es el vector de ganancia relativa para\(\boldsymbol{k}^{\prime}\), por lo que no hay una manera inmediatamente obvia de encontrar una\(\boldsymbol{k}^{\prime}\) que satisfaga (3.50), y no hay garantía a priori de que esta ecuación tenga incluso una solución. El siguiente teorema, sin embargo, dice que esta es la única condición requerida para asegurar que\(\boldsymbol{k}^{\prime}\) es la política dinámica óptima en cada etapa (nuevamente utilizando\(\boldsymbol{w}^{\prime}\) como vector de recompensa final).

Teorema 3.6.1

Supongamos que\ ref {3.50} está satisfecho por alguna política\(\boldsymbol{k}^{\prime}\) donde la cadena de Markov para\(\boldsymbol{k}^{\prime}\) es una unicadena y\(\boldsymbol{w}^{\prime}\) es el vector de ganancia relativa de\(\boldsymbol{k}^{\prime}\). Entonces la política dinámica óptima, utilizando\(\boldsymbol{w}^{\prime}\) como vector de recompensa final, es la política estacionaria\(\boldsymbol{k}^{\prime}\). Además, la ganancia óptima en cada etapa\(n\) viene dada por

\[\boldsymbol{v}^{*}\left(n, \boldsymbol{w}^{\prime}\right)=\boldsymbol{w}^{\prime}+n g^{\prime} \boldsymbol{e}\label{3.51} \]

donde\(g^{\prime}=\boldsymbol{\pi}^{\prime} \boldsymbol{r}^{\boldsymbol{k}^{\prime}}\) y\(\boldsymbol{\pi^{\prime}}\) es el vector de estado estacionario para\(\boldsymbol{k}^{\prime}\).

Prueba

Hemos visto desde\ ref {3.45} que\(\boldsymbol{k}^{\prime}\) es una decisión dinámica óptima en la etapa 1. También, dado que\(\boldsymbol{w}^{\prime}\) es el vector de ganancia relativa para\(\boldsymbol{k}^{\prime}\), el Teorema 3.5.2 afirma que si\(\boldsymbol{k}^{\prime}\) se usa la decisión en cada etapa, entonces la ganancia agregada satisface\(\boldsymbol{v}\left(n, \boldsymbol{w}^{\prime}\right)=n g^{\prime} \boldsymbol{e}+\boldsymbol{w}^{\prime}\). Dado que\(\boldsymbol{k}^{\prime}\) es óptimo en la etapa 1, se deduce que\ ref {3.51} está satisfecho para\(n=1\).

Ahora utilizamos la inducción sobre\(n\), con\(n=1\) como base, para verificar\ ref {3.51} y la optimalidad de esta misma\(\boldsymbol{k}^{\prime}\) en cada etapa\(n\). Así, supongamos que\ ref {3.51} está satisfecho por\(n\). Luego, desde (3.48),

\ (\ begin {aligned}
\ boldsymbol {v} ^ {*}\ left (n+1,\ boldsymbol {w} ^ {\ prime}\ right) &=\ max _ {\ boldsymbol {k}}\ left\ {\ boldsymbol {r} ^ {\ boldsymbol {k}} +\ left [\ boldsymbol {P^ {k}}\ derecho]\ boldsymbol {k} dsymbol {v} ^ {*}\ izquierda (n,\ negridsymbol {w} ^ {\ prime}\ derecha)\ derecha\} & (3.52)\\
&=\ max _ {\ negritasímbolo {k} }\ izquierda\ {\ negritasímbolo {r} ^ {\ negridsymbol {k}} +\ izquierda [\ boldsymbol {P^ {\ boldsymbol {k}}}}\ derecha]\ izquierda\ {\ negritas {w} ^ {\ prime} +n g^ {\ prime}\ símbolo en negrilla {e}\ derecha\}\ derecha\} & (3.53)\\
&=n g^ {\ prime}\ negritasímbolo {e} +\ max _ {\ negridsymbol {k}}\ izquierda\ {\ negritasímbolo {r} ^ {\ boldsymbol {k}} +\ left [\ negritasímbolo {P^ {k}}\ derecha] \ negridsymbol {w} ^ {\ prime}\ derecha\} & (3.54)\\
&\ izquierda. =n g^ {\ prime}\ negridsymbol {e} +\ negridsymbol {r} ^ {\ boldsymbol {k} ^ {\ prime}} +\ left [\ negritas {P^ {k^\ prime}}\ derecha]\ negridsymbol {w} ^ {\ prime}\ derecha\} & (3.55)\\
& =( n+1) g^ {prime\}\ negridsymbol {e} +\ negridsymbol {w} ^ {\ prime}. & (3.56)
\ final {alineado}\)

Eqn\ ref {3.53} se desprende de la hipótesis inductiva de (3.51),\ ref {3.54} sigue porque\(\left[P^{\boldsymbol{k}}\right] \boldsymbol{e}=\boldsymbol{e}\) para todos\(\boldsymbol{k}\),\ ref {3.55} se desprende de (3.50), y\ ref {3.56} se desprende de la definición de\(\boldsymbol{w}^{\prime}\) como el vector de ganancia relativa para\(\boldsymbol{k}^{\prime}\). Esto verifica\ ref {3.51} para\(n+1\). También, dado que\(\boldsymbol{k}^{\prime}\) maximiza (3.54), también maximiza (3.52), mostrando que\(\boldsymbol{k}^{\prime}\) es la decisión dinámica óptima en etapa\(n+1\). Esto completa el paso inductivo.

Dado que nuestro mayor interés en las políticas estacionarias es ayudar a comprender la relación entre la política dinámica óptima y las políticas estacionarias, definimos una política estacionaria óptima de la siguiente manera:

Definición 3.6.1

Una política estacionaria unichain\(\boldsymbol{k}^{\prime}\) es óptima si la política dinámica óptima con\(\boldsymbol{w}^{\prime}\) como recompensa final usa\(\boldsymbol{k}^{\prime}\) en cada etapa.

Esta definición da un paso por alto a varios temas importantes. Primero, podríamos estar interesados en la programación dinámica para algún otro vector de recompensa final. ¿Es posible que la programación dinámica funcione mucho mejor en algún sentido con un vector de recompensa final diferente? ¿Es posible que haya otra política estacionaria, especialmente una con mayor ganancia por etapa? Respondemos a estas preguntas más adelante y encontramos que las políticas estacionarias que son óptimas de acuerdo con la definición sí tienen ganancia máxima por etapa en comparación con políticas dinámicas con vectores arbitrarios de recompensa final.

Del Teorema 3.6.1, vemos que si hay una política\(\boldsymbol{k}^{\prime}\) que es un unichain con vector de ganancia relativa\(\boldsymbol{w}^{\prime}\), y si eso\(\boldsymbol{k}^{\prime}\) es una solución a (3.50), entonces\(\boldsymbol{k}^{\prime}\) es una política estacionaria óptima.

Es fácil imaginar modelos de decisión de Markov para los cuales cada política corresponde a una cadena de Markov con múltiples clases recurrentes. Existen muchos casos especiales de este tipo de situaciones, y su estudio detallado es inapropiado en un tratamiento introductorio. El problema esencial con este tipo de modelos es que es posible adentrarse en diversos conjuntos de estados de los que no hay salida, sin importar qué decisiones se utilicen. Estos conjuntos podrían tener diferentes ganancias, por lo que no hay ganancia general significativa por etapa. Evitamos estas situaciones mediante una suposición de modelado llamada accesibilidad inherente, que asume, para cada par\((i, j)\) de estados, que hay algún vector de decisión\(\boldsymbol{k}\) que contiene una ruta de\(i\) a\(j\).

El concepto de accesibilidad inherente es un poco complicado, ya que no dice lo mismo se\(\boldsymbol{k}\) puede utilizar para todos los pares de estados (es decir, que hay algunos\(\boldsymbol{k}\) para los que la cadena de Markov es recurrente). Como se muestra en el Ejercicio 3.31, sin embargo, la accesibilidad inherente implica que para cualquier estado\(j\), existe una\(\boldsymbol{k}\) para la cual\(j\) es accesible desde todos los demás estados. Como hemos visto varias veces, esto implica que la cadena de Markov para\(\boldsymbol{k}\) es una unicaína en la que\(j\) es un estado recurrente.

Cualquier modelo deseado puede ser modificado para satisfacer la accesibilidad inherente creando algunas nuevas decisiones con recompensas negativas muy grandes; estas permiten tales caminos pero los desalientan mucho. Esto nos permitirá construir políticas de unicaína óptimas, pero también usar la apariencia de estas grandes recompensas negativas para señalar que había algo cuestionable en el modelo original.

Mejora de políticas y búsqueda de políticas estacionarias óptimas

La idea general de mejora de políticas es comenzar con una política estacionaria de unicaína arbitraria\(\boldsymbol{k}^{\prime}\) con un vector de ganancia relativa\(\boldsymbol{w}^{\prime}\) (según lo dado por (3.37)). Asumimos la accesibilidad inherente a lo largo de esta sección, por lo que tales unichains deben existir. Luego verificamos si (3.50), está satisfecho, y si es así, sabemos por el Teorema 3.6.1 que\(\boldsymbol{k}^{\prime}\) es una política estacionaria óptima. Si no, encontramos otra política estacionaria\(\boldsymbol{k}\) que es 'mejor' que\(\boldsymbol{k}^{\prime}\) en un sentido que se describirá más adelante. Desafortunadamente, la política 'mejor' que encontremos podría no ser una unichain, por lo que también será necesario convertir esta nueva política en una política de unichain igualmente 'buena'. Aquí es donde se necesita la suposición de accesibilidad inherente. El algoritmo entonces encuentra iterativamente mejores y mejores políticas estacionarias unichain, hasta que finalmente una de ellas satisface\ ref {3.50} y por lo tanto es óptima.

Ahora declaramos el algoritmo de mejora de políticas para problemas de decisión de Markov inherentemente alcanzables. Este algoritmo es una generalización del algoritmo de mejora de políticas de Howard, [How60].

Algoritmo de Mejoramiento

1. Elegir una política de unichain arbitraria\(\boldsymbol{k}^{\prime}\)
2. Para póliza\(\boldsymbol{k}^{\prime}\), calcular\(\boldsymbol{w}^{\prime}\) y\(g^{\prime}\) desde\(\boldsymbol{w}^{\prime}+g^{\prime} \boldsymbol{e}=\boldsymbol{r}^{\boldsymbol{k}^{\prime}}+\left[P^{\boldsymbol{k}^{\prime}}\right] \boldsymbol{w}^{\prime}\) y\(\boldsymbol{\pi}^{\prime} \boldsymbol{w}^{\prime}=0\).
3. Si\(\boldsymbol{r}^{\boldsymbol{k}^{\prime}}+\left[P^{\boldsymbol{k}^{\prime}}\right] \boldsymbol{w}^{\prime}=\max _{\boldsymbol{k}}\left\{\boldsymbol{r}^{\boldsymbol{k}}+\left[P^{\boldsymbol{k}}\right] \boldsymbol{w}^{\prime}\right\}\), entonces detente;\(\boldsymbol{k}^{\prime}\) es óptimo.
4. De lo contrario, elija\(\ell\) y\(k_{\ell}\) para que\(r_{\ell}^{\left(k_{\ell}^{\prime}\right)}+\sum_{j} P_{\ell j}^{\left(k_{\ell}^{\prime}\right)} w_{j}^{\prime}<r_{\ell}^{\left(k_{\ell}\right)}+\sum_{j} P_{\ell j}^{\left(k_{\ell}\right)} w_{j}^{\prime}\). Para\(i \neq \ell\), vamos\(k_{i}=k_{i}^{\prime}\).
5. Si no\(\boldsymbol{k}=\left(k_{1}, \ldots k_{\mathrm{M}}\right)\) es un unichain, entonces deja\(\mathcal{R}\) ser la clase recurrente en\(\boldsymbol{k}\) ese estado contiene\(\ell\), y deja\(\tilde{\boldsymbol{k}}\) ser una política unichain para la cual\(\tilde{k}_{i}=k_{i}\) para cada uno\(i \in \mathcal{R}\). Alternativamente, si ya\(\boldsymbol{k} \) es un unichain, vamos\(\tilde{\boldsymbol{k}}=\boldsymbol{k}\).
6. Actualizar\(\boldsymbol{k}^{\prime}\) al valor de\(\tilde{\boldsymbol{k}}\) y volver al paso 2.

Si falla la prueba de detención en el paso 3, debe haber una\(\ell\) y\(k_{\ell}\) para la cual\(r_{\ell}^{\left(k_{\ell}^{\prime}\right)}+\sum_{j} P_{\ell j}^{\left(k_{\ell}^{\prime}\right)} w_{j}^{\prime}< r_{\ell}^{\left(k_{\ell}\right)}+\sum_{j} P_{\ell j}^{\left(k_{\ell}\right)} w_{j}^{\prime}\). Así, el paso 4 siempre se puede ejecutar si el algoritmo no se detiene en el paso 3, y dado que la decisión se cambia solo para el estado único\(\ell\), la política resultante\(\boldsymbol{k}\) satisface

\[\boldsymbol{r}^{\boldsymbol{k}^{\prime}}+\left[p^{\boldsymbol{k}^{\prime}}\right] \boldsymbol{\boldsymbol { w }}^{\prime} \leq \boldsymbol{r}^{\boldsymbol{k}}+\left[P^{\boldsymbol{k}}\right] \boldsymbol{w}^{\prime} \quad \text { with strict inequality for component } \ell\label{3.57} \]

Los tres siguientes lemmas consideran los diferentes casos para el estado\(\ell\) cuya decisión se cambia en el paso 4 del algoritmo. Tomados en conjunto, muestran que cada iteración del algoritmo aumenta la ganancia por etapa o mantiene constante la ganancia por etapa mientras aumenta el vector de ganancia relativa. Después de probar estos lemas, volvemos a mostrar que el algoritmo debe converger y explicar el sentido en que el algoritmo estacionario resultante es óptimo.

Para cada uno de los lemmas, deje\(\boldsymbol{k}^{\prime}\) ser el vector de decisión en el paso 1 de una iteración dada del algoritmo de mejora de políticas y supongamos que la cadena de Markov para\(\boldsymbol{k}^{\prime}\) es una unichain. Let\(g^{\prime}, \boldsymbol{w}^{\prime}\), y\(\mathcal{R}^{\prime}\) respectivamente ser la ganancia por etapa, el vector de ganancia relativa, y el conjunto recurrente de estados para\(\boldsymbol{k}^{\prime}\). Supongamos que la condición de parada en el paso 3 no se satisface y eso\(\ell\) denota el estado cuya decisión se cambia. \(k_{\ell}\)Sea la nueva decisión en el paso 4 y deje que\(\boldsymbol{k}\) sea el nuevo vector de decisión.

Lema 3.6.1

Asumir eso\(\ell \in \mathcal{R}^{\prime}\). Entonces la cadena de Markov para\(\boldsymbol{k}\) es una unicaína y\(\ell\) es recurrente en\(\boldsymbol{k}\). La ganancia por etapa g para\(\boldsymbol{k}\) satisface\(g>g^{\prime}\).

Prueba

La cadena de Markov para\(\boldsymbol{k}\) es la misma que para\(\boldsymbol{k}^{\prime}\) excepto por las transiciones fuera del estado\(\ell\). Así, cada camino hacia\(\ell\)\(\boldsymbol{k}^{\prime}\) adentro sigue siendo un camino hacia\(\ell\) adentro\(\boldsymbol{k}\). Ya que\(\ell\) es recurrente en la unicaína\(\boldsymbol{k}^{\prime}\), es accesible desde todos los estados en\(\boldsymbol{k}^{\prime}\) y por lo tanto en\(\boldsymbol{k}\). Se deduce (ver Ejercicio 3.3) que\(\ell\) es recurrente en\(\boldsymbol{k}\) y\(\boldsymbol{k}\) es una unicaína. Desde\(\boldsymbol{r}^{\boldsymbol{k}^{\prime}}+\left[P^{\boldsymbol{k}^{\prime}}\right] \boldsymbol{w}^{\prime}=\boldsymbol{w}^{\prime}+g^{\prime} \boldsymbol{e}\) (véase (3.37)), podemos reescribir\ ref {3.57} como

\[\boldsymbol{w}^{\prime}+g^{\prime} \boldsymbol{e} \leq \boldsymbol{r}^{k}+\left[P^{k}\right] \boldsymbol{w}^{\prime} \quad \text { with strict inequality for component } \ell\label{3.58} \]

Premultiplicando ambos lados de\ ref {3.58} por el vector de estado estacionario\(\pi\) de la cadena de Markov\(\boldsymbol{k}\) y usando el hecho de que\(\ell\) es recurente y por lo tanto\(\pi_{\ell}>0\),

\(\boldsymbol{\pi} \boldsymbol{w}^{\prime}+g^{\prime}<\boldsymbol{\pi} \boldsymbol{r^{k}}+\boldsymbol{\pi}\left[\boldsymbol{P^{k}}\right] \boldsymbol{w}^{\prime}\)

Ya que\(\boldsymbol{\pi}\left[\boldsymbol{P^{k}}\right]=\boldsymbol{\pi}\), esto simplifica a

\[g^{\prime}<\boldsymbol{\pi} \boldsymbol{r}^{k}\label{3.59} \]

La ganancia por etapa\(g\) para\(\boldsymbol{k}\) es\(\boldsymbol{\pi r^{k}}\), así que tenemos\(g^{\prime}<g\).

Lema 3.6.2

Supongamos que\(\ell \notin \mathcal{R}^{\prime}\) (\(\ell\)es decir, es transitorio en\(\boldsymbol{k}^{\prime}\)) y que los estados de no\(\mathcal{R}^{\prime}\) son accesibles desde\(\ell\) adentro\(\boldsymbol{k}\). Entonces no\(\boldsymbol{k}\) es una unicaína y\(\ell\) es recurrente en\(\boldsymbol{k}\). \(\tilde{\boldsymbol{k}}\)Existe un vector de decisión que es una unicadena para la cual\(\tilde{k}_{i}=k_{i}\) para\(i \in \mathcal{R}\), y su ganancia por etapa\(\tilde{g}\) satisface\(\tilde{g}>g\).

Prueba

Ya que\(\ell \notin \mathcal{R}^{\prime}\), las probabilidades de transición de los estados de\(\mathcal{R}^{\prime}\) no han cambiado al pasar de\(\boldsymbol{k}^{\prime}\) a\(\boldsymbol{k}\). Así, el conjunto de estados accesibles desde\(\mathcal{R}^{\prime}\) permanece sin cambios, y\(\mathcal{R}^{\prime}\) es un conjunto recurrente de\(\boldsymbol{k}\). Dado que no\(\mathcal{R}^{\prime}\) es accesible desde\(\ell\), debe haber otro conjunto recurrente,, en\(\mathcal{R}\)\(\boldsymbol{k}\), y por lo tanto no\(\boldsymbol{k}\) es un unichain. Los estados accesibles desde ya\(\mathcal{R}\) no incluyen\(\mathcal{R}^{\prime}\), y dado que\(\ell\) es el único estado cuyas probabilidades de transición han cambiado, todos los estados en\(\mathcal{R}\) tienen caminos hacia\(\ell\) adentro\(\boldsymbol{k}\). De ello se deduce que\(\ell \in \mathcal{R}\).

Ahora dejemos\(\boldsymbol{\pi}\) ser el vector de estado estacionario para\(\mathcal{R}\) en la cadena de Markov para\(\boldsymbol{k}\). Ya que\(\pi_{\ell}>0\),\ ref {3.58} y\ ref {3.59} siguen siendo válidos para esta situación. Dejar\(\tilde{\boldsymbol{k}}\) ser un vector de decisión para el cual\(\tilde{k}_{i}=k_{i}\) para cada uno\(i \in \mathcal{R}\). Usando la accesibilidad inherente, también podemos elegir\(\tilde{k}_{i}\) para cada uno para\(i \notin \mathcal{R}\) que\(\ell\) sea accesible desde\(i\) (ver Ejercicio 3.31). Así\(\tilde{\boldsymbol{k}}\) es una unicaína con la clase recurrente\(\mathcal{R}\). Ya que\(\tilde{\boldsymbol{k}}\) tiene las mismas probabilidades de transición y recompensas en\(\mathcal{R}\) como\(\boldsymbol{k}\), vemos eso\(\tilde{g}=\pi \boldsymbol{r}^{\boldsymbol{k}}\) y así\(\tilde{g}>g^{\prime}\).

El lema final ahora incluye todos los casos no en Lemmas 3.6.1 y 3.6.2

Teorema 3.6.3

Supongamos que\(\ell \notin \mathcal{R}^{\prime}\) y eso\(\mathcal{R}^{\prime}\) es accesible desde\(\ell\) adentro\(\boldsymbol{k}\). Entonces\(\boldsymbol{k}\) es una unicaína con el mismo conjunto recurrente\(\mathcal{R}^{\prime}\) que\(\boldsymbol{k}^{\prime}\). La ganancia por etapa\(g\) es igual a\(g^{\prime}\) y el vector de ganancia\(\boldsymbol{w}\) relativa de\(\boldsymbol{k}\) satisface

\[\boldsymbol{w}^{\prime} \leq \boldsymbol{w} \quad \text { with } w_{\ell}^{\prime}<w_{\ell} \text { and } w_{i}^{\prime}=w_{i} \text { for } i \in \mathcal{R}^{\prime}\label{3.60} \]

Prueba

Dado que\(\boldsymbol{k}^{\prime}\) es un unichain,\(\boldsymbol{k}^{\prime}\) contiene una ruta de cada estado a\(\mathcal{R}^{\prime}\). Si tal camino no pasa por estado\(\ell\), entonces\(\boldsymbol{k}\) también contiene ese camino. Si tal camino pasa por\(\ell\), entonces ese camino puede ser reemplazado\(\boldsymbol{k}\) por el mismo camino a\(\ell\) seguido por un camino\(\boldsymbol{k}\) de entrada de\(\ell\) a\(\mathcal{R}^{\prime}\). Así\(\mathcal{R}^{\prime}\) es accesible desde todos los estados en\(\boldsymbol{k}\). Dado que los estados accesibles desde no\(\mathcal{R}^{\prime}\) cambian de\(\boldsymbol{k}^{\prime}\) a\(\boldsymbol{k}\),\(\boldsymbol{k}\) sigue siendo una unicadena con el conjunto recurrente\(\mathcal{R}^{\prime}\) y el estado\(\ell\) sigue siendo transitorio.

Si escribimos la ecuación definitoria\ ref {3.37} para\(\boldsymbol{w}^{\prime}\) componente por componente, obtenemos

\[w_{i}^{\prime}+g^{\prime}=r_{i}^{k_{i}^{\prime}}+\sum_{j} P_{i j}^{k_{i}^{\prime}} w_{j}^{\prime}\label{3.61} \]

Considera i el conjunto de estas ecuaciones para las cuales\(i \in \mathcal{R}^{\prime}\). Dado que\(P_{i j}^{k_{i}^{\prime}}=0\) para todos los transitorios\(j\) en\(\boldsymbol{k}^{\prime}\), estas son las mismas ecuaciones de ganancia relativa que para la cadena de Markov restringida a\(\mathcal{R}^{\prime}\). Por lo tanto\(\boldsymbol{w}^{\prime}\), se define de manera única\(i \in \mathcal{R}_{i}^{\prime}\) por este conjunto restringido de ecuaciones. Estas ecuaciones no se cambian al pasar de\(\boldsymbol{k}^{\prime}\) a\(\boldsymbol{k}\), por lo que se deduce que\(w_{i}=w_{i}^{\prime}\) para\(i \in \mathcal{R}^{\prime}\). También hemos visto que el vector de estado estacionario\(\boldsymbol{\pi}^{\prime}\) está determinado únicamente por las probabilidades de transición en la clase recurrente, por lo\(\boldsymbol{\pi}^{\prime}\) que no cambia de\(\boldsymbol{k}^{\prime}\) a\(\boldsymbol{k}\), y\(g=g^{\prime}\).

Finalmente, considere la diferencia entre las ecuaciones de ganancia relativa para\(\boldsymbol{k}^{\prime}\) en 3.61 y aquellas para\(\boldsymbol{k}\). Dado que\(g^{\prime}=g\),

\[w_{i}-w_{i}^{\prime}=r_{i}^{k_{i}}-r_{i}^{k_{i}^{\prime}}+\sum_{j}\left(P_{i j}^{k_{i}} w_{j}-P_{i j}^{k_{i}^{\prime}} w_{j}^{\prime}\right)\label{3.62} \]

Para todos\(i \neq \ell\), esto simplifica

\[w_{i}-w_{i}^{\prime}=\sum_{j} P_{i j}^{k_{i}}\left(w_{j}-w_{j}^{\prime}\right)\label{3.63} \]

Para\(i=\ell\),\ ref {3.62} se puede reescribir como

\[w_{\ell}-w_{\ell}^{\prime}=\sum_{j} P_{\ell j}^{k_{\ell}}\left(w_{j}-w_{j}^{\prime}\right)+\left[r_{\ell}^{k_{\ell}}-r_{\ell}^{k_{\ell}^{\prime}}+\sum_{j}\left(P_{\ell j}^{k_{\ell}} w_{j}^{\prime}-P_{\ell j}^{k_{\ell}^{\prime}} w_{j}^{\prime}\right)\right]\label{3.64} \]

La cantidad entre paréntesis debe ser positiva por el paso 4 del algoritmo, y la denotamos como\(\hat{r}_{\ell}-\hat{r}_{\ell}^{\prime}\). Si también definimos\(\hat{r}_{i}=\hat{r}_{i}^{\prime}\) for\(i \neq \ell\), entonces podemos aplicar la última parte de Corolario 3.5.1 (usando\(\hat{\boldsymbol{r}}\) y\(\hat{\boldsymbol{r}}^{\prime}\) como vectores de recompensa) para concluir eso\(\boldsymbol{w} \geq \boldsymbol{w}^{\prime}\) con\(w_{\ell}>w_{\ell}^{\prime}\).

Ahora vemos que cada iteración del algoritmo aumenta la ganancia por etapa o mantiene la ganancia por etapa igual y aumenta el vector de ganancia relativa\(\boldsymbol{w}\). Así, la secuencia de políticas que encuentra el algoritmo nunca puede repetirse. Dado que hay un número finito de políticas estacionarias, el algoritmo debe terminar eventualmente en el paso 3. Esto significa que la política dinámica óptima que utiliza el vector de recompensa final\(\boldsymbol{w}^{\prime}\) para el vector de decisión de terminación\(\boldsymbol{k}^{\prime}\) debe ser de hecho la política estacionaria\(\boldsymbol{k}^{\prime}\).

Ahora surge la pregunta de si la política dinámica óptima que usa algún otro vector de recompensa final puede ser sustancialmente mejor que la que usa\(\boldsymbol{w}^{\prime}\). La respuesta es bastante simple y se desarrolla en el Ejercicio 3.30. Se muestra allí que si\(\boldsymbol{u}\) y\(\boldsymbol{u}^{\prime}\) son vectores arbitrarios de recompensa final utilizados en el algoritmo de programación dinámica, entonces\(v^{*}(n, \boldsymbol{u})\) y\(v^{*}\left(n, \boldsymbol{u}^{\prime}\right)\) están relacionados por

\(v^{*}(n, \boldsymbol{u}) \leq v^{*}\left(n, \boldsymbol{u}^{\prime}\right)+\alpha \boldsymbol{e},\)

donde\(\alpha=\max _{i}\left(u_{i}-u_{i}^{\prime}\right)\). Usando\(\boldsymbol{w}^{\prime}\) for\(\boldsymbol{u}^{\prime}\), se ve que la ganancia por etapa de la programación dinámica i, con cualquier vector de recompensa final, es como mucho la ganancia\(g^{\prime}\) de la política estacionaria al finalizar el algoritmo de mejora de políticas.

Los resultados anteriores se resumen en el siguiente teorema.

Teorema 3.6.2

Para cualquier problema de decisión de Markov en estado finito inherentemente alcanzable, el algoritmo de mejora de políticas termina con una política estacionaria\(\boldsymbol{k}^{\prime}\) que es la misma que la solución al algoritmo de programación dinámica que\(\boldsymbol{w}^{\prime}\) se usa como vector de recompensa final. La ganancia por etapa\(g^{\prime}\) de esta política estacionaria maximiza la ganancia por etapa sobre todas las políticas estacionarias y sobre todos los vectores de recompensa final para el algoritmo de programación dinámica.

Un problema restante es la cuestión de si el vector de ganancia relativa encontrado por el algoritmo de mejora de políticas es en algún sentido óptimo. El ejemplo de la Figura 3.11 ilustra dos soluciones diferentes que terminan el algoritmo de mejora de políticas. Cada uno tiene la misma ganancia (como lo garantiza el Teorema 3.6.2) pero sus vectores de ganancia relativa no están ordenados.

En muchas aplicaciones como las variaciones en el problema de la ruta más corta, el tema interesante es lo que sucede antes de ingresar a la clase recurrente, y a menudo solo hay una clase recurrente y un conjunto de decisiones dentro de esa clase de interés. El siguiente corolario muestra que en este caso, el vector de ganancia relativa para la política estacionaria que termina el algoritmo es máximo no sólo entre las políticas visitadas por el algoritmo sino entre todas las políticas con la misma clase recurrente y las mismas decisiones dentro de esa clase. El comprobante es casi el mismo que el de Lemma 3.6.3 y se lleva a cabo en el Ejercicio 3.33.

Figura 3.11: Un problema de decisión de Markov en el que hay dos vectores de decisión unicaína (uno a la izquierda y otro a la derecha). Para cada uno, se satisface\ ref {3.50} y la ganancia por etapa es 0. El algoritmo de programación dinámica (sin recompensa final) es estacionario pero tiene dos clases recurrentes, una de las cuales es {3}, usando la decisión 2 y la otra es {1, 2}, usando la decisión 1 en cada estado.

Corolario 3.6.1

Supongamos que el algoritmo de mejora de políticas termina con la clase\(\mathcal{R}^{\prime}\) recurrente\(\boldsymbol{k}^{\prime}\), el vector de decisión y el vector de ganancia relativa\(\boldsymbol{w}^{\prime}\). Entonces, para cualquier política estacionaria que tenga la clase recurrente\(\mathcal{R}^{\prime}\) y un vector de decisión\(\boldsymbol{k}\) satisfactorio\(k_{i}=k_{i}^{\prime}\) para todos\(i \in \mathcal{R}^{\prime}\), el vector de ganancia relativa\(\boldsymbol{w}\) satisface\(\boldsymbol{w} \leq \boldsymbol{w}^{\prime}\).

---

Referencia

¹³ Desafortunadamente, muchos problemas de programación dinámica de interés tienen un enorme número de estados y posibles elecciones de decisión (la llamada maldición de la dimensionalidad), y así, aunque las ecuaciones son simples, los requisitos computacionales podrían estar más allá del rango de factibilidad práctica.