7.2: El retraso en la cola en una cola G/G/1

Antes de analizar las caminatas aleatorias en general, introducimos dos áreas problemáticas importantes que a menudo se ven mejor en términos de caminatas aleatorias. En esta sección, el retardo de cola en una cola G/G/1 se representa como un problema de cruce de umbral en una caminata aleatoria. En la siguiente sección, la probabilidad de error en un tipo estándar de problema de detección se representa como un problema de caminata aleatoria. Este problema de detección luego se generalizará a un problema de detección secuencial basado en cruces de umbral en una caminata aleatoria.

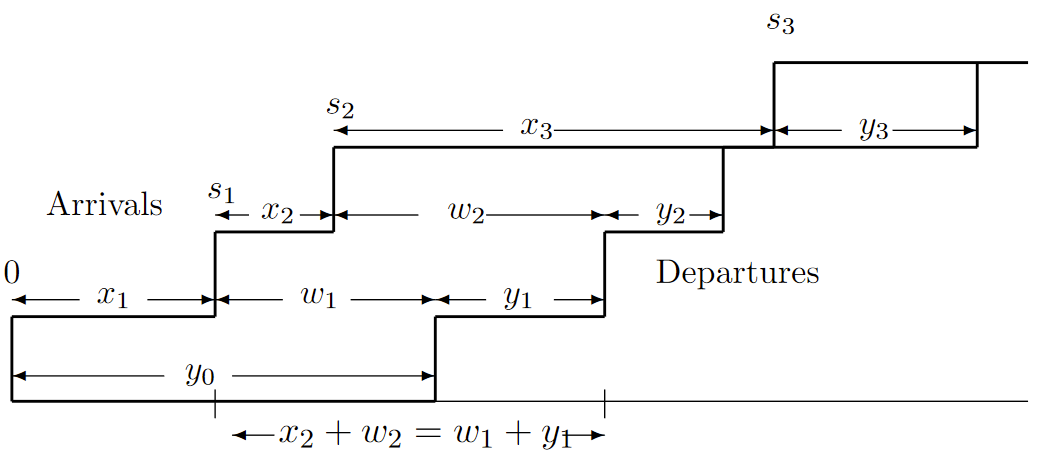
Considere una cola G/G/1 con el servicio primero en venir, primero en servir (FCFS). Asociaremos la probabilidad de que un cliente deba esperar más de un tiempo dado\(\alpha \) en la cola con la probabilidad de que una cierta caminata aleatoria cruce un umbral en\(\alpha \). Dejados\( X_1, X_2, . . .\) ser los tiempos de interllegada de un sistema de colas G/G/1; así estas variables son IID con una función de distribución arbitraria\(F_X \ref{x} =\) Pr {\( X_i ≤ x\)}. Supongamos que la llegada 0 entra en un sistema vacío en el tiempo 0, y así\( S_n = X_1 +X_2 + ... +X_n\) es la época de la\(n^{th}\) llegada después del tiempo 0. Dejar\(Y_0, Y_1, . . . ,\) ser los tiempos de servicio de los sucesivos clientes. Estos son independientes de {\( X_i; i ≥ 1 \)} y son IID con alguna función de distribución dada\( F_Y (y)\). La Figura 7.2 muestra las llegadas y salidas para una ruta de muestra ilustrativa del proceso e ilustra el retraso de la cola para cada llegada.

Figura 7.2: Ruta muestral de llegadas y salidas de una cola G/G/1. El cliente 0 llega a la hora 0 y entra en servicio de inmediato. El Cliente 1 llega a la hora\( s_1 = x_1 \). Para el caso que se muestra arriba, el cliente 0 aún no ha salido\( i.e., \, x_1 < y_0\), por lo que el tiempo del cliente 1 en cola es\( w_1 = y_0 − x_1\). Como se ilustra, el tiempo del sistema del cliente 1 (tiempo de cola más tiempo de servicio) es\( w_1 + y_1 \). El Cliente 2 llega a\( s_2 = x_1 + x_2\). Para el caso que se muestra arriba, esto es antes de que el cliente 1 salga a las\( y_0 + y_1\). Así, la espera del cliente 2 en cola es\(w_2 = y_0 + y_1 − x_1 − x_2\). Como se ilustra anteriormente, también\(x_2 +w_2\) es igual al tiempo del sistema del cliente 1, entonces\(w_2 = w_1 +y_1 −x_2\). El cliente 3 llega cuando el sistema está vacío, por lo que entra en servicio inmediatamente sin esperar en cola,\(i.e., \, w_3 = 0\).

Deje\( W_n\) ser el retraso en la cola para el\( n^{th}\) cliente,\( n ≥ 1\). El tiempo del sistema para el cliente\( n\) se define entonces como el retraso en la cola\(W_n\) más el tiempo de servicio\( Y_n\). Como se ilustra en la Figura 7.2, el cliente\( n ≥ 1\) llega unidades de\( X_n \) tiempo después del inicio del tiempo\(n − 1\) del sistema del cliente. Si\( X_n < W_{n−1} + Y_{n−1}, \, i.e.\), si el cliente\( n\) llega antes del final de la hora\( n − 1\) del sistema del cliente, entonces el cliente\( n\) debe esperar en la cola hasta que\( n\) termine el servicio (en la figura, por ejemplo, el cliente 2 llega mientras el cliente 1 todavía está en la cola). Así

\[ W_n = W_{n-1} +Y_{n-1} - X_n \qquad \text{if } X_n \leq W_{n-1} + Y_{n-1} . \nonumber \]

Por otro lado, si\( X_n > W_{n−1} + Y_{n−1} \), entonces el cliente\(n−1\) (y todos los clientes anteriores) han partido cuando\( n\) llega. Así\( n\) inicia el servicio de inmediato y\( W_n = 0\). Este es el caso del cliente 3 en la figura. Estos dos casos se pueden combinar en una sola ecuación

\[ W_n = \text{max} [W_{n-1} + Y_{n-1} - X_n , 0]; \qquad \text{for } n \geq 1; \qquad W_0 = 0 \nonumber \]

Dado que\( Y_{n−1}\) y\( X_n\) se acoplan entre sí en esta ecuación para cada uno\(n\), es conveniente definir\( U_n = Y_{n−1} − X_n\). Tenga en cuenta que {\( U_n; n ≥ 1\)} es una secuencia de variables aleatorias IID. De (7.4)\( W_n = \text{max}[W_{n−1} + U_n, 0]\), e iterando sobre esta ecuación,

\[ \begin{aligned} W_n \quad &= \quad \text{max}[\text{max} [ W_{n-2} + U_{n-1}, \, 0] \\ &= \quad \text{max} [ ( W_{n-2} + U_{n-1} + U_n , \, 0 ] \\ &= \quad \text{max} [ ( W_{n-3} + U_{n-2}+ U_{n-1}+U_n), \, (U_{n-1} + U_n), \, U_n, \, 0] \\ &= \quad ... \quad ... \\ &= \quad \text{max} [(U_1 + U_2 + ... + U_n), \quad (U_2+U_3+...+U_n), ... , (U_{n-1}+U_n), \, U_n , \, 0 ]. \end{aligned} \nonumber \]

No es necesario para el teorema a continuación, pero podemos entender mejor esta maximización al darnos cuenta de que si la maximización se logra en\( U_i + U_{i+1} + ...+ U_n\), entonces un periodo ocupado debe comenzar con la llegada del cliente\( i − 1\) y continuar al menos a través del servicio del cliente\(n\). Para ver esto intuitivamente, tenga en cuenta que el análisis anterior inicia con la llegada del cliente 0 a un sistema vacío en el tiempo 0, pero la elección de 0 tiempo y número de cliente 0 no tiene nada que ver con el análisis, y así el análisis es válido para cualquier llegada a un sistema vacío. Elegir el mayor número de clientes antes de\( n\) que comience un período ocupado debe entonces dar el retraso correcto en la cola, y así maximizar (7.5). El ejercicio 7.2 proporciona más información sobre esta maximización.

Definir\( Z_n = U_n\)\( Z_n = U_n + U_{n−1}\), definir y en general, para\( i ≤ n\), definir\( Z^n_i = U_n +U_{n−1} + ... + U_{n−i+1} \). Así\( Z_n^n = U_n + ... + U_1\). Con estas definiciones,\ ref {7.5} se convierte

\[ W_n = \text{max} [ 0,Z_1^n,Z_2^n, ... ,Z_n^n] . \nonumber \]

Tenga en cuenta que los términos en {\( Z^n_i; 1 ≤ i ≤ n\)} son los primeros\( n\) términos de una caminata aleatoria, pero no es la caminata aleatoria basada en\( U_1, U_2, . . . ,\) sino más bien la caminata aleatoria que va hacia atrás, comenzando por\( U_n\). Obsérvese también que\( W_{n+1}\), por ejemplo, es el máximo de un conjunto diferente de variables\(i.e.\),, es la caminata que va hacia atrás desde\( U_{n+1}\). Afortunadamente, esto no importa para el análisis ya que las variables ordenadas (\( U_n, U_{n−1} . . . , U_1 )\)son estadísticamente idénticas a (\( U_1, . . . , U_n)\). La probabilidad de que la espera sea mayor o igual que un valor dado\( \alpha \) es

\[ \text{Pr} \{ W_n \geq \alpha \} = \text{Pr} \{ \text{max} [0,Z^n_1,Z^n_2,...,Z^n_n ] \geq \alpha \} . \nonumber \]

Esto dice que, para el\( n^{th}\) cliente, Pr {\( W_n ≥ \alpha \)} es igual a la probabilidad de que la caminata aleatoria {\( Z_n; 1 ≤ i ≤ n\)} cruce un umbral en\(\alpha\) por el\(n^{th}\) juicio. Debido a la\(i\) inicialización utilizada en el análisis, vemos que\(W_n\) es el retraso en la cola de la\(n^{th}\) llegada después del inicio de un período ocupado (aunque esta\(n^{th}\) llegada podría pertenecer a un período ocupado posterior a ese período ocupado inicial)

Como se señaló anteriormente, (Un, Un−1,.., U1) es estadísticamente idéntico a (U1,.., Un). Esto significa que Pr {Wn ≥ α} es la misma que la probabilidad de que los primeros n términos de una caminata aleatoria basada en {Ui; i ≥ 1} crucen un umbral en α. Dado que los primeros n + 1 términos de esta caminata aleatoria brindan una oportunidad más de cruzar α que los primeros n términos, vemos que

\[ ... \leq \text{Pr} \{ W_n \geq \alpha \} \leq \text{Pr} \{ W_{n+1} \geq \alpha \} \leq ... \leq 1 . \nonumber \]

Dado que esta secuencia de probabilidades no es decreciente, debe tener un límite as\(n\rightarrow \infty \), y este límite se denota Pr {\(W ≥ \alpha \)}. Matemáticamente, ¹ este límite es la probabilidad de que una caminata aleatoria basada en {\( U_i; i ≥ 1\)} alguna vez cruce un umbral en\( \alpha \). Físicamente, este límite es la probabilidad de que el retraso de la cola sea al menos α para cualquier cliente de numeración muy grande dado (\( i.e. \), para el cliente\(n\) cuando la influencia de un período ocupado comenzando\( n\) clientes antes se haya extinguido). Estos resultados se resumen en el siguiente teorema.

Teorema 7.2.1

Sea {\(X_i; i ≥ 1\)} los intervalos entre llegadas IID de una cola G/G/1, que {\(Y_i; i ≥ 0\)} sean los tiempos de servicio IID y supongamos que el sistema está vacío en el momento 0 cuando llega el cliente 0. Deje\(W_n\) ser el retraso en la cola para el\(n^{th}\) cliente. Dejar\(U_n = Y_{n−1} −X_n\)\(n ≥ 1\) y dejar\(Z_i^n = U_n + U_{n−1} + ... + U{n−i+1} \) para\(1 ≤ i ≤ n\). Entonces para cada\( \alpha > 0\), y\( n ≥ 1, \, W_n = \text{max}[0, Z^1_n, Z^2_n, . . . , Z_n^n\)]. Además, Pr {\(W_n ≥ \alpha \)} es la probabilidad de que la\(n \) caminata aleatoria basada en {\( U_i; i ≥ 1\)} cruce un umbral\(\alpha\) en o antes del\( n^{th}\) juicio. Finalmente, Pr {\(W ≥ \alpha \} = \text{lim}_{n\rightarrow \infty}\)Pr {\(W_n ≥ \alpha\)} es igual a la probabilidad de que la caminata aleatoria basada en {\( U_i; i ≥ 1 \)} alguna vez cruce un umbral en\( \alpha\).

Tenga en cuenta que el teorema especifica la función de distribución de\(W_n\) para cada uno\(n\), pero no dice nada sobre la distribución conjunta de retardos sucesivos de colas. Estos no son lo mismo que la distribución de términos sucesivos en una caminata aleatoria debido a la inversión de términos anteriores.

Encontraremos un límite superior relativamente simple y aproximación a la probabilidad de que una caminata aleatoria cruce un umbral positivo en la Sección 7.4. A partir del Teorema 7.2.1, esto se puede aplicar a la distribución del retardo de cola para la cola G/G/1 (y así también a las colas M/G/1 y M/M/1).

__________________________________

1. Más precisamente, la secuencia de retrasos en la cola\(W_1, W_2 . . . ,\) convergen en distribución a\(W , \, i.e., \, \text{lim}_n F_{W_n} \ref{w} = F_{W} (w)\) para cada uno\(w\). Nos referimos\( W\) como el retraso en la cola en estado estacionario.