7.3: Detección, Decisiones y Pruebas de Hipótesis

Consideremos una situación en la que hacemos observaciones\(n\) ruidosas del resultado de una sola variable aleatoria discreta\(H\) y luego adivinamos, sobre la base de las observaciones solamente, qué valor muestral de\(H\) ocurrió. En la tecnología de la comunicación, esto se denomina problema de detección. Modela, por ejemplo, la situación en la que se transmite un símbolo a través de un canal de comunicación y se reciben observaciones\(n\) ruidosas. De manera similar modela el problema de detectar si un objetivo está presente o no en una observación por radar. En la teoría del control, tales situaciones suelen denominarse problemas de decisión, mientras que en la estadística, se les hace referencia tanto como pruebas de hipótesis como problemas de inferencia estadística.

Los problemas de comunicación, control y estadística anteriores son básicamente los mismos, por lo que discutimos todos ellos usando la terminología de pruebas de hipótesis. Así, los valores de muestra del rv se\(H\) denominan hipótesis. Asumimos a lo largo de esta sección que\(H\) tiene sólo dos valores posibles. Las situaciones donde\(H\) tiene más de 2 valores generalmente se pueden ver en términos de múltiples decisiones binarias.

No hace diferencia en el análisis de hipótesis binarias probando cómo se llaman las dos hipótesis, por lo que simplemente las denotamos como hipótesis 0 e hipótesis 1. Así\(H\) es un rv binario y abreviamos su PMF como\(\text{p}_H \ref{0} = p_0 \) y\(\text{p}_H \ref{1} = p_1\). Así\(p_0\) y\(p_1 = 1 − p_0\) son las probabilidades a priori ¹ para los dos valores de muestra (hipótesis) de la variable aleatoria\(H\).

\(\boldsymbol{Y} = (Y_1, Y_2, . . . , Y_n)\)Dejen ser las\(n\) observaciones. Supongamos, por simplicidad inicial, que estas variables, condicionales\(H = 0\) o\(H = 1\), tienen densidades condicionales conjuntas\(f_{\boldsymbol{Y} |H} (\boldsymbol{y} | 1)\),\(f_{\boldsymbol{Y} |H} (\boldsymbol{y} | 0)\) y, que son estrictamente positivas sobre su región común de definición. El caso de importancia primaria en esta sección (y el caso donde los paseos aleatorios son útiles) es aquel en el que, condicionados a un valor de muestra dado de\(H\), los rv\(Y_1, . . . , Y_n\) son IID. Aun asumiendo por simplicidad que las observaciones tienen densidades, digamos\(f_{\boldsymbol{Y} |H} (y | \ell) \) para\(\ell = 0\) o\(\ell = 1\), la densidad conjunta, condicionada\(H = \ell\), viene dada por

\[ f_{\boldsymbol{Y}|H}(\boldsymbol{y}|\ell ) = \prod^n_{i=1} f_{Y|H} (y_i|\ell ) \nonumber \]

Tenga en cuenta que todos los componentes de\(\boldsymbol{Y}\) están condicionados al mismo\(H, \, i.e.\), para un solo valor de muestra de\( H\), hay valores de muestra\(n\) correspondientes de\(Y\).

Supongamos que es necesario ² para seleccionar un valor de muestra\( H\) sobre la base del valor muestral\(\boldsymbol{y}\) de las\( n\) observaciones. Por lo general, es posible que la selección (decisión) sea incorrecta, por lo que distinguimos el valor muestral\( h\) del resultado experimental real del valor muestral\(\hat{h}\) de nuestra selección. Es decir, el resultado del experimento especifica\(h\) y\(\boldsymbol{y}\), pero sólo\(\boldsymbol{y}\) se observa. La selección\(\hat{h}\), basada únicamente en\(\boldsymbol{y}\), podría ser desigual a h. Decimos que se ha producido un error si\(\hat{h} \neq h \)

Ahora analizamos tanto cómo tomar decisiones como evaluar la probabilidad de error resultante. Dada una muestra particular de n observaciones\( \boldsymbol{y} = y_1, y_2, . . . , y_n,\) podemos evaluar Pr\(\{ H=0 | \boldsymbol{y}\}\) como

\[ \text{Pr}\{ H=0|\boldsymbol{y} \} = \dfrac{p_0 f_{\boldsymbol{Y}|H} (\boldsymbol{y} | 0)}{p_0f_{\boldsymbol{Y}|H} (\boldsymbol{y}|0)+p_1 f_{\boldsymbol{Y}|H} (\boldsymbol{y}|1)} \nonumber \]

Podemos evaluar Pr {\(H=1 | \boldsymbol{y}\)} de la misma manera La relación de estas cantidades viene dada por

\[ \dfrac{ \text{Pr} \{H=0 | \boldsymbol{y} \} }{ \text{Pr} \{H=1 | \boldsymbol{y} \}}= \dfrac{ p_0 f_{\boldsymbol{Y} |H} (\boldsymbol{y} |0)}{p_1 f_{\boldsymbol{Y} |H} (\boldsymbol{y} |1)} \nonumber \]

Para un dado\(\boldsymbol{y}\), si seleccionamos\(\hat{h} = 0\), entonces se hace un error si\(h = 1\). La probabilidad de este evento es Pr {\(H = 1 | \boldsymbol{y}\)}. Del mismo modo, si seleccionamos\(\hat{h} = 1\), la probabilidad de error es Pr {\(H = 0 | \boldsymbol{y}\)}. Así se minimiza la probabilidad de error, para un dado\(\boldsymbol{y}\), seleccionando\(\hat{h} =0\) si la relación en (7.3.3) es mayor que 1 y seleccionando\(\hat{h}=1\) lo contrario. Si la relación es igual a 1, la probabilidad de error es la misma si se selecciona\(\hat{h}=0 \) o\(\hat{h}=1\) se selecciona, por lo que arbitrariamente seleccionamos\(\hat{h}= 1\) para hacer la regla determinista.

La regla anterior para elegir\(\hat{H}=0\) o\(\hat{H}=1\) se denomina regla de detección de probabilidad máxima a posteriori, abreviada como regla MAP. Dado que minimiza la probabilidad de error para cada uno\(\boldsymbol{y}\), también minimiza la probabilidad de error general como una expectativa sobre\(\boldsymbol{Y}\) y\(H\).

La estructura de la prueba MAP se vuelve más clara si definimos la razón de verosimilitud\( \Lambda (\boldsymbol{y})\) para la decisión binaria como

\[ \Lambda (\boldsymbol{y}) = \dfrac{f_{\boldsymbol{Y}|H}(\boldsymbol{y}|0)}{f_{\boldsymbol{Y}|H}(\boldsymbol{y}|1)} \nonumber \]

La razón de verosimilitud es función únicamente de la observación\(\boldsymbol{y}\) y no depende de las probabilidades a priori. Hay un rv correspondiente\( \Lambda (\boldsymbol{Y} )\) que es una función ³ de\(\boldsymbol{Y}\), pero tenderemos a tratar con los valores de muestra. La prueba MAP ahora se puede declarar de manera compacta como

\[ \Lambda (\boldsymbol{y}) \quad \left\{ \begin{array}{cc} > p_1/p_0 \quad ; & \qquad \text{select }\hat{h}=0 \\ \\ \leq p_1/p_0 \quad ; & \qquad \text{select }\hat{h}=1 \end{array} \right. \nonumber \]

Para el caso primario de interés, donde las n observaciones son IID condicionales a H, la razón de
verosimilitud viene dada por

\[ \Lambda (\boldsymbol{y}) = \prod^n_{i=1} \dfrac{f_{Y|H}(y_i|0)}{f_{Y|H}(y_i|1)} \nonumber \]

La prueba MAP entonces toma una forma más atractiva si tomamos el logaritmo de cada lado en (7.3.4). El logaritmo de\(\Lambda (\boldsymbol{y})\) es entonces una suma de\(n\) términos,\(\sum^n_{i=1} z_i\), donde\(z_i\) viene dado por

\[ z_i = \ln \dfrac{f_{Y|H}(y_i|0)}{f_{Y|H}(y_i|1)} \nonumber \]

El valor de la muestra\(z_i\) se llama la relación logarítmica de verosimilitud de\(y_i\) para cada\( i\), y\( \ln \Lambda (\boldsymbol{y})\) se llama la relación logarítmica de\(\boldsymbol{y}\) La prueba en (7.3.4) se expresa entonces como

\[ \sum^n_{i=1} z_i \left\{ \begin{array}{cc} >\ln (p_1/p_0) \quad ; & \qquad \text{select } \hat{h}=0 \\ \\ \leq \ln (p_1/p_0) \quad ; & \qquad \text{select } \hat{h}=1 \end{array} \right. \nonumber \]

Como se podría imaginar, las relaciones de verosimilitud logarítmica son mucho más convenientes para trabajar que las relaciones de
probabilidad cuando se trata condicionalmente de IID rv.

Ejemplo 7.3.1. Considera un proceso de Poisson para el que la tasa de llegada\(\lambda\) podría ser\(\lambda_0\) o podría ser\(\lambda_1\). Asumir\(i \in \{0, 1\}\), para, esa\(p_i\) es la probabilidad a priori de que la tasa sea\(\lambda_i\). Supongamos que observamos las primeras\(n\) llegadas,\(Y_1, . . . Y_n\) y tomamos una decisión MAP sobre la tasa de llegada a partir de los valores de la muestra\(y_1, . . . , y_n\).

Las densidades de probabilidad condicional para las observaciones\(Y_1, . . . , Y_n\) vienen dadas por

\[ f_{\boldsymbol{Y}|H}(\boldsymbol{y} |i) = \prod^n_{i=1} \lambda_i e^{-\lambda_iy_i} \nonumber \]

La prueba en (7.3.5) luego se convierte

\[ n \ln (\lambda_0/\lambda_1)+\sum^n_{i=1} (\lambda_1-\lambda_0) y_i \left\{ \begin{array}{cc} >\ln (p_1/p_0) \quad ; & \qquad \text{select } \hat{h}=0 \\ \\ \leq \ln (p_1/p_0) \quad ; & \qquad \text{select } \hat{h}=1 \end{array} \right. \nonumber \]

Tenga en cuenta que la prueba depende\(\boldsymbol{y}\) solo a través de la hora de la llegada\(n\) th. Esto no debería sorprendernos, ya que sabemos que, bajo cada hipótesis, las primeras\(n − 1\) llegadas se distribuyen de manera uniforme condicionada a\( n\) la hora de llegada.

La prueba MAP en (7.3.4), y el caso especial en (7.3.5), son ejemplos de pruebas de umbral. Es decir, en (7.3.4), se toma una decisión calculando la razón de verosimilitud y comparándola con un umbral\(\eta = p_1/p_0\). En (7.3.5), se compara la relación\( \ln (\Lambda (\boldsymbol{y}))\) log-verosimilitud con\(\ln \eta = \ln (p_1/p_0)\).

Hay una serie de otras formulaciones de pruebas de hipótesis que también conducen a pruebas de umbral, aunque en estas formulaciones alternativas, el umbral no\(\eta > 0\) necesita ser igual a\(p_1/p_0\), y de hecho las probabilidades a priori ni siquiera necesitan definirse. En particular, entonces, la prueba umbral at\(\eta \) se define por

\[ \Lambda (\boldsymbol{y}) \left\{ \begin{array}{cc} > \eta \quad ; & \qquad \text{select } \hat{h}=0 \\ \\ \leq \eta \quad ; & \qquad \text{select } \hat{h}=1 \end{array} \right. \nonumber \]

Por ejemplo, la detección de máxima verosimilitud (ML) selecciona hipótesis\(\hat{h} = 0\) si\(f_{\boldsymbol{Y} |H} (\boldsymbol{y} | 0) > f_{\boldsymbol{Y} |H} (\boldsymbol{y} | 1)\), y selecciona\( \hat{h} = 1\) lo contrario. Por lo tanto, la prueba ML es una prueba umbral con\(\eta = 1\). Tenga en cuenta que la detección de ML es equivalente a la detección de MAP con probabilidades iguales a priori, pero puede ser utilizada en muchos otros casos, incluyendo aquellos con probabilidades a priori indefinidas.

En muchas situaciones de detección hay costos desiguales, digamos\(C_0\) y\( C_1\), asociados a los dos tipos de errores. Por ejemplo, un tipo de error en un pronóstico médico podría llevar a una enfermedad grave y el otro a una operación innecesaria. Una decisión de costo mínimo podría entonces minimizar el costo esperado sobre los dos tipos de errores. Como se muestra en el Ejercicio 7.5, esta es también una prueba de umbral con el umbral\(\eta = (C_1p_1)/(C_0p_0)\). Este ejemplo también ilustra que, aunque asignar costos a errores proporciona un enfoque racional para la toma de decisiones, puede que no haya una manera ampliamente aceptable de asignar costos.

Por último, considere la situación en la que un tipo de error, digamos Pr {e|\(H=1\)} está delimitado por la parte superior por algún límite tolerable\(\alpha\) y Pr {e|\(H=0\)} se minimiza sujeto a esta restricción. La solución a esto se llama la regla Neyman-Pearson. La regla de Neyman-Pearson es de particular interés ya que no requiere ninguna suposición sobre las probabilidades a priori. La siguiente subsección muestra que la regla de Neyman-Pearson es esencialmente una prueba de umbral, y explica por qué rara vez se miran pruebas distintas a las pruebas de umbral.

curva de error y t Ney Man-Pearson rul e

Cualquier prueba,\(i.e.\), cualquier regla determinista para seleccionar una hipótesis binaria a partir de una observación\(\boldsymbol{y}\), puede verse como una función ⁴ mapeando cada observación posible\(\boldsymbol{y}\) a 0 o 1. Si definimos\(A\) como el conjunto de\(n\) -vectores\(\boldsymbol{y}\) que se mapean a la hipótesis 1 para una prueba dada, entonces la prueba puede ser identificada por su conjunto correspondiente\( A\).

Dada la prueba\(A\), las probabilidades de error, dadas\(H = 0\) y\(H = 1\) respectivamente, están dadas por

\[ \text{Pr} \{ \boldsymbol{Y} \in A|H=0\} ; \qquad \text{Pr} \{ \boldsymbol{Y} \in A_c|H=1\} \nonumber \]

Tenga en cuenta que estas probabilidades de error condicional dependen únicamente de la prueba\(A\) y no de las probabilidades a priori. Abreviaremos estas probabilidades de error como

\[ q_0 \ref{A} = \text{Pr} \{ \boldsymbol{Y} \in A |H=0 \} ; \qquad q_1(A) = \text{Pr} \{ \boldsymbol{Y} \in A^c|H=1 \} \nonumber \]

Para probabilidades dadas a priori,\(p_0\) y\(p_1\), la probabilidad de error general es

\[ \text{Pr\{e}(A) \} = p_0q_0(A)+p_1q_1(A) \nonumber \]

Si\(A\) es una prueba de umbral, con umbral\(\eta\), el conjunto\( A\) viene dado por

\[ A = \left\{ \boldsymbol{y} \, : \, \dfrac{f_{\boldsymbol{Y}|H}(\boldsymbol{y}|0)}{f_{\boldsymbol{Y}|H}(\boldsymbol{y}|1)} \leq \eta \right\} \nonumber \]

Dado que las pruebas de umbral juegan un papel muy especial aquí, abusamos de la notación usando\(\eta\) en lugar de\(A\) para referirnos a una prueba de umbral en\(\eta\). Ahora podemos caracterizar la relación entre las pruebas de umbral y otras pruebas. El siguiente lema se ilustra en la Figura 7.3.

Lema 7.3.1. Considera una gráfica bidimensional en la que las probabilidades de error para cada prueba\(A\) se trazan como (\(q_1(A), q_0(A)\)). Entonces para cualquier prueba de umbral\(\eta , 0 < \eta < \infty \), y cualquiera\(A\), el punto (\(q_1(A), q_0(A)\)) está en el medio plano cerrado por encima y a la derecha de una línea recta de pendiente\(−\eta\) que pasa por el punto\( (q_1(\eta ), q_0(\eta ))\).

Prueba: Para cualquier dado\(\eta \), considere las probabilidades a priori ⁵\((p_0, p_1)\) para las cuales\(\eta = p_1/p_0\). La probabilidad de error general para la prueba\( A\) usando estas probabilidades a priori es entonces

\[ \text{Pr\{e}(A)\} = p_0q_0 \ref{A} +p_1q_1(A) = p_0[q_0(A)+\eta q_1(A)] \nonumber \]

Del mismo modo, la probabilidad de error global para la prueba de umbral\(\eta \) usando las mismas probabilidades a priori es

\[ \text{Pr\{e}(\eta) \} = p_0q_0(\eta ) +p_1q_1(\eta ) = p_0 [ q_0(\eta )+\eta q_1(\eta) ] \nonumber \]

Esta última probabilidad de error es la probabilidad de error MAP para el dado\(p_0, p_1\), y por lo tanto es la probabilidad mínima de error general (para el dado\( p_0, p_1\)) sobre todas las pruebas. Por lo tanto

\[ q_0(\eta ) + \eta q_1(\eta ) \leq q_0 \ref{A} + \eta q_1(A) \nonumber \]

Como se muestra en la figura, estos son los puntos en los que las líneas de pendiente\(−\eta \) desde\((q_1(A), q_0(A))\) y\((q_1(\eta ), q_0(\eta ))\) respectivamente cruzan el eje de ordenadas. Así todos los puntos de la primera línea (incluyendo se\((q_1(A), q_0(A)))\) encuentran en el medio plano cerrado arriba y a la derecha de todos los puntos en la segunda, completando la prueba.

\(\square \)

La línea recta de pendiente\( −\eta \) a través del punto\( (q_1(\eta ), q_0(\eta ))\) tiene la ecuación\( f_{\eta}(\alpha) = q_0(\eta) + \eta (q_1(\eta ) − \alpha)\). Dado que el lema es válido para todos\(\eta , 0 < \eta < \infty \), el punto\((q_1(A), q_0(A))\) para una prueba arbitraria se encuentra arriba y a la derecha de toda la familia de líneas rectas que, para cada una\(\eta \), pasan\((q_1(\eta ), q_0(\eta ))\) con pendiente\(-\eta \). Esta familia de líneas rectas tiene una envolvente superior llamada curva de error,\(u(\alpha)\), definida por

\[ u(\alpha ) = \sup_{0\leq \eta < \infty} q_0(\eta )+\eta (q_1(\eta )-\alpha ) \nonumber \]

El lema asevera entonces que para cada prueba\(A\) (incluyendo las pruebas de umbral), tenemos\(u(q_1(A)) \leq q_0(A)\). Además, dado que cada prueba de umbral se encuentra en una de estas líneas rectas, y por lo tanto sobre o por debajo de la curva\(u(\alpha )\), vemos que las probabilidades de error\((q_1(\eta ), q_0(\eta)\) para cada prueba umbral deben estar en la curva\(u(\alpha )\). Finalmente, dado que cada línea recta que define\(u(\alpha )\) forma una tangente de\( u(\alpha )\) y se encuentra sobre o por debajo\(u(\alpha )\), la función\(u(\alpha )\) es convexa. ⁶ La Figura 7.4 ilustra la curva de error.

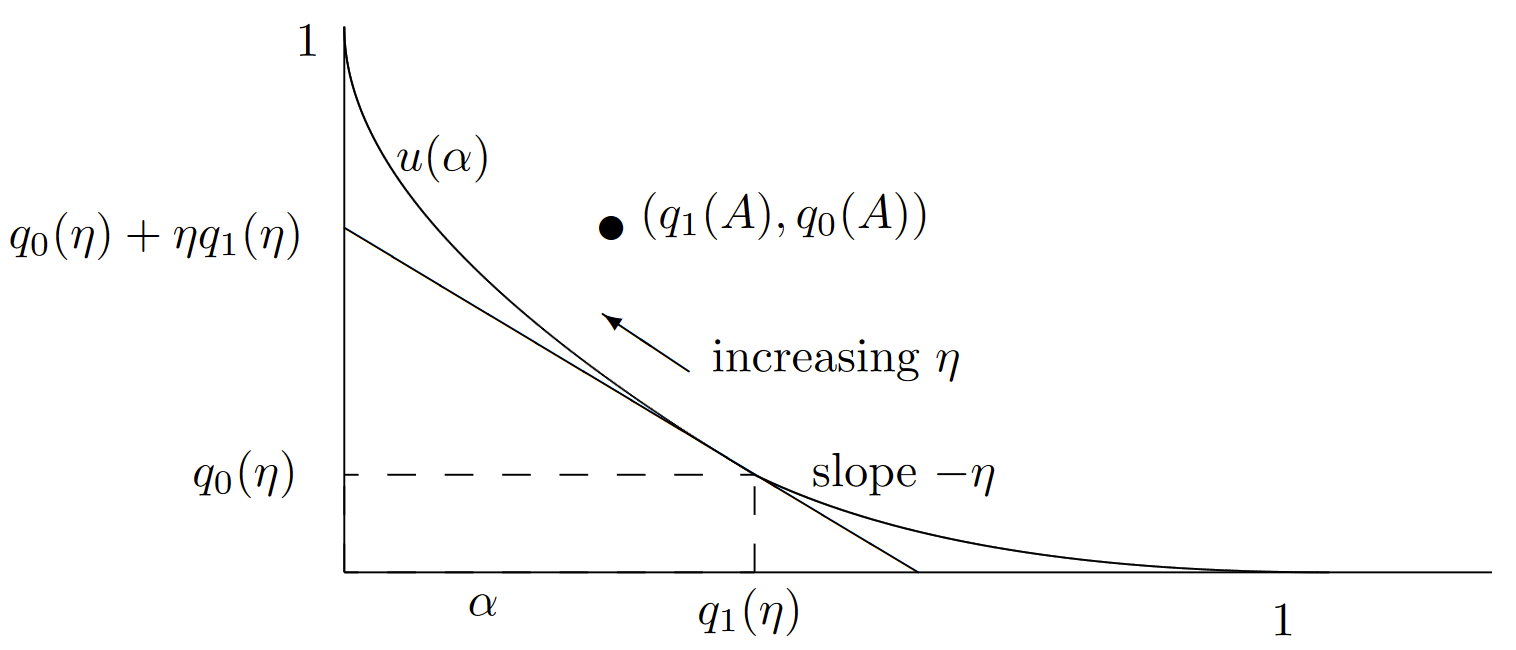
Figura 7.4: Ilustración de la curva de error\(u(\alpha )\) (ver (7.3.7)). Tenga en cuenta que\(u(\alpha )\) es convexo, se encuentra sobre o por encima de sus tangentes, y sobre o debajo de todas las pruebas. También se puede observar, ya sea directamente desde la curva anterior o desde la definición de una prueba de umbral, que no\(q_1(\eta )\) está aumentando\(\eta\) y\(q_0(\eta )\) no decreciente.

La curva de error esencialmente nos da una compensación entre la probabilidad de error dada\(H = 0\) y la dada\(H = 1\). Las pruebas de umbral, ya que se encuentran en la curva de error, proporcionan puntos óptimos para esta compensación.

El argumento anterior carece de una característica importante. Aunque todas las pruebas de umbral se encuentran en la curva de error, no hemos demostrado que todos los puntos de la curva de error correspondan a las pruebas de umbral. De hecho, como muestra el siguiente ejemplo, a veces es necesario generalizar las pruebas de umbral por aleatorización para llegar a todos los puntos de la curva de error.

Antes de continuar con este ejemplo, tenga en cuenta que Lemma 7.3.1 y la definición de la curva de error se aplican a un conjunto de modelos más amplio de lo discutido hasta ahora. Primero, el lema aún se mantiene si\(f_{\boldsymbol{Y} |H} (\boldsymbol{y} | \ell )\) es cero sobre un conjunto arbitrario de\(\boldsymbol{y}\) para una o ambas hipótesis\(\ell \). La razón de verosimilitud\(\Lambda (\boldsymbol{y})\) es infinita donde\( f_{\boldsymbol{Y} |H} (\boldsymbol{y} | 0) > 0\) y\(f_{\boldsymbol{Y} |H} (\boldsymbol{y} | 1) = 0\), pero esto no afecta la prueba del lema. El ejercicio 7.6 ayuda a explicar cómo esta situación puede afectar la curva de error.

Además, se puede ver que el lema también sostiene si\(\boldsymbol{Y}\) es una\(n\) -tupla de rv discretas.El siguiente ejemplo explica más a fondo el caso discreto y también muestra por qué no todos los puntos de la curva de error corresponden a pruebas de umbral. Lo que asumimos a lo largo de todo\(\Lambda(\boldsymbol{Y} )\) es que es un rv condicional\(H = 1\) y es un condicional posiblemente defectuoso ⁷ rv\( H = 0\).

Ejemplo 7.3.2 Acerca del ejemplo más simple de un problema de detección es que con una observación binaria unidimensional Y. Supongamos entonces que

\[ \text{p}_{Y|H} \ref{0|0} = \text{p}_{Y|H}(1|1) = \dfrac{2}{3}; \qquad \text{p}_{Y|H}(0|1) = \text{p}_{Y|H}(1|0)=\dfrac{1}{3} \nonumber \]

Así la observación\(Y\) es igual\( H\) con probabilidad 2/3. La regla de decisión 'natural' sería seleccionar\(\hat{h}\) para estar de acuerdo con la observación\( y\), cometiendo así un error con probabilidad 1/3, tanto condicional como\(H = 0\).\(H = 1\) Es fácil verificar a partir de (7.3.4) (usando PMF's en lugar de densidades) que esta regla 'natural' es la regla MAP si las probabilidades a priori están en el rango\(1/3 ≤ p_1 < 2/3\).

Porque\( p_1 < 1/3\), se puede ver que la regla del MAP es\(\hat{h} = 0\), sin importar cuál sea la observación. Intuitivamente, la hipótesis 1 es demasiado improbable a priori para ser superada por la evidencia cuando\(Y = 1\). De igual manera\(p_1 ≥ 2/3\), si, entonces la regla MAP selecciona\(\hat{h} = 1\), independiente de la observación.

La prueba de umbral correspondiente (ver (7.3.6)) selecciona\(\hat{h} = y\) para\(1/2 ≤ \eta < 2\). Selecciona\(\hat{h} = 0\) para\(\eta < 1/2\) y\(\hat{h} = 1\) para\(\eta ≥ 2\). Esto significa que, aunque hay una prueba de umbral para cada uno\(\eta\), solo hay 3 pares de probabilidad de error resultantes,\(i.e., \, (q_1(\eta ), q_0(\eta )\) pueden ser (0, 1) o (1/3, 1/3), o (1, 0). El primer par aguanta para\(\eta ≥ 2\), el segundo para\(1/2 ≤ \eta < 2\), y el tercero para\(\eta< 1/2\). Esto se ilustra en la Figura 7.5.

Acabamos de ver que hay una prueba de umbral para cada uno\(\eta , \, 0 < \eta< \infty \), pero esas pruebas de umbral se mapean a solo 3 puntos distintos\((q_1(\eta ), q_0(\eta ))\). Como puede verse, la curva de error une estos 3 puntos por líneas rectas.

Veamos con más cuidado la tangente de pendiente -1/2 a través del punto (1/3, 1/3). Esto corresponde a la prueba MAP en\( \text{p}_1 = 1/3\). Como se ve en (7.3.4), esta prueba MAP selecciona\(\hat{h} = 1\) para\(y = 1\) y\(\hat{h} = 0\) para\( y = 0\). La selección de\(\hat{h} = 1\) cuándo\( y = 1\) es una elección que no importa en la que seleccionar\(\hat{h} = 0\) produciría la misma probabilidad de error general, pero cambiaría\((q_1(\eta ), q_0(\eta )\) de (1/3, 1/3) a (1, 0).

No es difícil verificar (ya que solo hay 4 pruebas,\(i.e.\), reglas deterministas, para mapear una variable binaria a otra variable binaria) que ninguna prueba puede lograr el compromiso entre\(q_1(A)\) e\(q_0(A)\) indicado por los puntos interiores en la línea recta entre (1/3, 1/3) y (1, 0). Sin embargo, si usamos una regla aleatoria, mapeando 1 a 1 con probabilidad\(\theta\) y en 0 con probabilidad\(1 − \theta\) (junto con siempre mapear 0 a 0), entonces todos los puntos en la línea recta de (1/3, 1/3) a (1, 0) se logran como\(\theta\) va de 0 a 1. En otras palabras, una elección que no le importe para el MAP se convierte en una opción importante en el equilibrio entre\(q_1(A)\) y\(q_0(A)\).

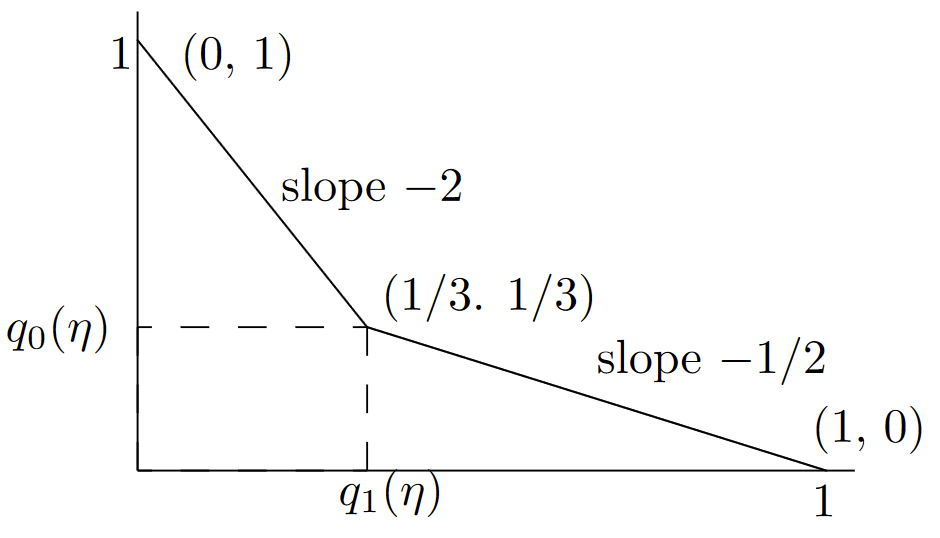
Figura 7.5: Ilustración de la curva de error\(u(\alpha )\) para el Ejemplo 7.3.2. Para todos\(\eta \) en el rango\(1/2 ≤ \eta < 2\), la prueba de umbral selecciona\(\hat{h} = y\). Las probabilidades de error correspondientes son entonces\(q_1(\eta ) = q_0(\eta ) = 1/3\). Para\(\eta< 1/2\), la prueba de umbral selecciona\(\hat{h} = 0\) para todos\( y\), y para\(\eta > 2\), selecciona\(\hat{h} = 1\) para todos\(y\). La curva de error (ver (7.3.7)) para los puntos a la derecha de (1/3, 1/3) se maximiza por la línea recta de pendiente -1/2 a través (1/3, 1/3). De igual manera, la curva de error para los puntos a la izquierda de (1/3, 1/3) se maximiza por la línea recta de pendiente -2 hasta (1/3, 1/3). Se pueden visualizar las líneas tangentes como una sierra de cerco invertida, primero ver-aserrando alrededor (0,1), luego alrededor (1/3, 1/3), y finalmente alrededor (1, 0).

De la misma manera, todos los puntos en la línea recta de (0, 1) a (1/3, 1/3) se pueden lograr mediante una regla aleatoria que mapee 0 a 0 con probabilidad dada\(\theta\) (junto con siempre mapear 1 a 1).

En el caso general, la curva de error puede contener segmentos de línea recta siempre que la función de distribución de la razón de verosimilitud, condicional\(H = 1\), sea discontinua. Este es siempre el caso de las observaciones discretas y, como se ilustra en el Ejercicio 7.6, también podría ocurrir con observaciones continuas. Para entender esto, supongamos que Pr {\(\Lambda (\boldsymbol{Y} ) = \eta | H=1\} = \beta > 0\)para algunos\(\eta , 0 < \eta < 1\). Entonces la prueba MAP en\(\eta \) tiene una región de probabilidad que no le importa\(\beta \) dada\( H = 1\). Esto significa que si se cambia la prueba MAP para resolver el caso de no importa a favor de\(H = 0\), entonces la probabilidad de error\(q_1\) se incrementa en\(\beta\) y la probabilidad de error\(q_0\) se disminuye en\(\eta \beta\). Lema 7.3.1 se ve fácilmente como válido sea cual sea la forma en que se resuelvan los casos de no atención, y así ambos\( (q_1, q_0)\) y se\( (q_1+\beta, q_0−\eta \beta)\) encuentran en la curva de error. Dado que todas las pruebas se encuentran por encima y a la derecha de la línea recta de pendiente\(−\eta \) a través de estos puntos, la curva de error tiene un segmento de línea recta entre estos puntos. Como se mencionó anteriormente, cualquier par de probabilidades de error en este segmento de línea recta se puede realizar mediante el uso de una prueba de umbral aleatorizada en\(\eta \).

La regla de Neyman-Pearson es la regla (aleatorizada donde sea necesario) que realiza cualquier par de probabilidad de error deseado\((q_1, q_0)\) en la curva de error,\(i.e\)., donde\(q_0 = u(q_1)\). Para ser específicos, asumir la restricción que\(q_1 = \alpha\) para cualquier dado\(\alpha , \, 0 < \alpha ≤ 1\). Dado que Pr {\(\Lambda (\boldsymbol{Y}) > \eta | H = 1\)} es una función de distribución complementaria, no está aumentando\(\eta \), quizás con discontinuidades escalonadas. At\(\eta = 0\), tiene el valor 1−Pr {\(\Lambda (\boldsymbol{Y} ) = 0\)}. A medida que\(\eta \) aumenta, disminuye a 0, ya sea para algunos finitos\(\eta \) o como\(\eta \rightarrow \infty\). Así si\(0 < \alpha ≤ 1 − \text{Pr}\{ \Lambda (\boldsymbol{Y} ) = 0\)}, vemos que\(\alpha \) es igual a Pr {\(\Lambda (\boldsymbol{y}) > \eta | H = 1\)} para algunos\(\eta \) o\(\alpha \) está en una discontinuidad escalonada en algunos\(\eta \). Definiendo\(\eta (\alpha )\) como un\(\eta \) lugar donde ocurre una de estas alternativas, ⁸ existe una solución a lo siguiente:

\[ \text{Pr} \{ \Lambda (\boldsymbol{y})>\eta (\alpha ) |H=1\} \leq \alpha \leq \text{Pr}\{ \Lambda (\boldsymbol{y}) \geq \eta (\alpha ) | H=1 \} \nonumber \]

Tenga en cuenta que (7.3.8) también se mantiene, con\(\eta (\alpha ) = 0\) si\(1 − \text{Pr}\{ \Lambda (\boldsymbol{Y} )=0 \} < \alpha ≤ 1. \)

La regla de Neyman-Pearson, dada\(\alpha \), es usar una prueba de umbral en\(\eta (\alpha )\) if Pr {\(\Lambda (\boldsymbol{y} )=\eta (\alpha ) | H=1 \} = 0\). Si Pr\(\{ \Lambda (\boldsymbol{y} )=\eta (\alpha ) | H=1\} > 0\), entonces se usa una prueba aleatoria en\(\eta (\alpha )\). Cuando\(\Lambda (\boldsymbol{y} ) = \eta (\alpha ), \, \hat{h}\) se elige para ser 1 con probabilidad\(\theta \) donde

\[ \theta = \dfrac{\alpha - \text{Pr} \{ \Lambda (\boldsymbol{y} )>\eta (\alpha )|H=1\} }{\text{Pr} \{ \Lambda (\boldsymbol{y} ) = \eta (\alpha ) | H=1\} } \nonumber \]

Esto se resume en el siguiente teorema:

Teorema 7.3.1. Suponga que la razón de verosimilitud\(\Lambda (\boldsymbol{Y})\) es un rv bajo\( H = 1\). Para cualquiera\(\alpha ,\, 0 < \alpha \leq 1\), la restricción que Pr {\(\text{e} | H = 1\} \leq \alpha \)implica que Pr {\(\text{e} | H = 0\} \geq u(\alpha )\)donde\(u(\alpha )\) está la curva de error. Además, se utiliza Pr {\(\text{e} | H = 0\} = u(\alpha )\)si la regla de Neyman-Pearson, especificada en (7.3.8) y (7.3.9).

Prueba: Hemos demostrado que la regla de Neyman-Pearson tiene las probabilidades de error estipuladas. Una regla de decisión arbitraria, aleatoria o no, puede especificarse mediante un conjunto finito de reglas\(A_1, . . . , A_k\) de decisión determinista junto con un rv\( V\), independiente de\(H\) y\(\boldsymbol{Y}\), con valores de muestra\(1, . . . , k\). Dejar que el PMF\(V\) sea\( (θ_1, . . . , θ_k)\), una regla de decisión arbitraria, dada\(\boldsymbol{Y} = \boldsymbol{y}\) y\(V = i\) es usar regla de decisión\(A_i\) si\(V = i\). Las probabilidades de error para esta regla son Pr {\(\text{e} | H=1\} = \sum^k_{i=1} θ_iq_1(A_i)\)y Pr {\(\text{e} | H=0\} = \sum^k_{i=1} θ_iq_0(A_i)\). Es fácil ver que Lemma 7.3.1 aplica a estas reglas aleatorias de la misma manera que a las reglas deterministas.

\( \square \)

Todas las reglas de decisión que hemos discutido son reglas de umbral, y en todas esas reglas, la primera parte de la regla de decisión es encontrar la razón de verosimilitud a\(\Lambda (\boldsymbol{y})\) partir de la observación\(\boldsymbol{y}\). Esto simplifica el problema de la prueba de hipótesis desde el procesamiento\(n\) de un vector dimensional\(\boldsymbol{y}\) hasta el procesamiento de un solo número\(\Lambda (\boldsymbol{y})\), y este es típicamente el componente principal para tomar una decisión de umbral. Cualquier cálculo intermedio\(\Lambda (\boldsymbol{y} )\) a partir de\(\boldsymbol{y}\) que permita ser calculado se denomina estadística suficiente. Estos suelen desempeñar un papel importante en la detección, especialmente para la detección en entornos ruidosos.

Hay algunos problemas de prueba de hipótesis en los que las reglas de umbral son en cierto sentido inapropiadas. En particular, el costo de un error bajo una u otra hipótesis podría ser altamente dependiente de la observación\(boldsymbol{y}\). Una prueba de umbral de costo mínimo para cada uno\(\boldsymbol{y}\) seguiría siendo apropiada, pero una prueba de umbral basada en la razón de verosimilitud podría ser inapropiada ya que diferentes observaciones con estructuras de costos muy diferentes podrían tener la misma relación de probabilidad. Es decir, en tales situaciones, la razón de verosimilitud ya no es suficiente para tomar una decisión de costo mínimo.

Hasta el momento hemos asumido que se toma una decisión después de un número predeterminado\(n\) de observaciones. En muchas situaciones, las observaciones son costosas e introducen un retraso no deseado en las decisiones. Se preferiría, después de un número dado de observaciones, tomar una decisión si la probabilidad de error resultante es lo suficientemente pequeña, y continuar con más observaciones de lo contrario. El sentido común dicta tal estrategia, y la rama de la teoría de la probabilidad que analiza tales estrategias se llama análisis secuencial. En cierto sentido, se trata de una generalización de las pruebas de Neyman-Pearson, que emplearon una compensación entre los dos tipos de errores. Aquí tendremos una compensación de tres vías entre los dos tipos de errores y el tiempo requerido para tomar una decisión.

Ahora volvemos al problema de prueba de hipótesis de mayor interés donde las observaciones, condicionadas a la hipótesis, son IID. En este caso, la razón logarítmica después de n observaciones es la suma\(S_n = Z_1 + Z_n\) de las\(n\) razones de verosimilitud logarítmica individual Así, aparte ··· de la cuestión de tomar una decisión después de cierto número de observaciones, la secuencia de proporciones logarítmicas de verosimilitud\(S_1, S_2, . . .\) es una caminata aleatoria.

Esencialmente, veremos que una forma apropiada de elegir cuántas observaciones hacer, con base en el resultado de las observaciones anteriores, es la siguiente: La probabilidad de error bajo cualquiera de las hipótesis se basa en\( S_n = Z_1 + ...+ Z_n\). Así veremos que una regla apropiada es elegir\(H=0\) si el valor muestral\(s_n\) de\( S_n\) es mayor que algún umbral positivo\(\alpha\), elegir _H1 si\( s_n ≤ \beta\) para algún umbral negativo\(\beta\), y continuar probando si el valor de la muestra no tiene superó cualquiera de los umbrales. Es decir, el tiempo de decisión para estos problemas de decisión secuencial es el momento en el que la caminata aleatoria correspondiente cruza un umbral. Se comete un error cuando se cruza el umbral incorrecto.

Ahora hemos visto que tanto el retraso de la cola en una cola G/G/1 como el problema de prueba de hipótesis secuencial anterior pueden verse como problemas de cruce de umbral para caminatas aleatorias. En la siguiente sección se inicia un estudio sistémico de tales problemas.

_____________________________________

1. Los estadísticos han argumentado desde los primeros días de la estadística sobre la 'validez' de elegir probabilidades a priori para las hipótesis a probar. Los estadísticos bayesianos se sienten cómodos con esta práctica y los no bayesianos no lo están. Ambos se sienten cómodos al elegir un modelo de probabilidad para las observaciones condicionales a cada hipótesis. Aquí tomamos un enfoque bayesiano, en parte para aprovechar el poder de un modelo de probabilidad completo, y en parte porque los resultados no bayesianos\(i.e.\), resultados que no dependen de las probabilidades a priori, suelen ser más fáciles de derivar e interpretar dentro de una colección de modelos de probabilidad utilizando diferentes opciones para las probabilidades a priori. Como se verá, el enfoque bayesiano también hace natural incorporar los resultados de observaciones anteriores en probabilidades actualizadas a priori para analizar observaciones posteriores. En defensa de los no bayesianos, señalar que los resultados de las pruebas estadísticas a menudo se utilizan en áreas de desacuerdo significativo en materia de políticas públicas, y es importante dar la apariencia de falta de sesgo. Los resultados estadísticos pueden estar sesgados de muchas maneras más sutiles que el uso de probabilidades a priori, pero el uso de una distribución a priori es particularmente fácil de atacar.
2. En cierto sentido, es en la toma de decisiones donde el caucho se encuentra con el camino. Para situaciones del mundo real, un análisis probabilístico suele estar relacionado con el estudio del problema, pero eventualmente se debe elegir una tecnología u otra para un sistema, se debe contratar a una persona u otra para un trabajo, se debe aprobar una ley u otra, etc.
3. Obsérvese que en una formulación no bayesiana,\(\boldsymbol{Y}\) es un vector aleatorio diferente, en un espacio de probabilidad diferente, para\(H = 0\) que para\(H = 1\). Sin embargo, las probabilidades condicionales correspondientes para cada uno existen en cada espacio de probabilidad, y así\(\Lambda (\boldsymbol{Y} )\) existe (como un rv diferente) en cada espacio.
4. Por supuesto, la decisión debe tomarse con base en la observación\(\boldsymbol{y}\), por lo que una regla determinista se basa únicamente en\(\boldsymbol{y},\, i.e.\), es función de\(\boldsymbol{y}\). Veremos más adelante que se requieren reglas aleatorias en lugar de deterministas para algunos propósitos, pero tales reglas se llaman reglas aleatorias en lugar de pruebas.
5. Obsérvese que el lema no asume ninguna probabilidad a priori. La prueba MAP para cada elección a priori\((p_0, p_1)\) determina\(q_0(\eta )\) y\(q_1(\eta )\) para\(\eta = p_1/p_0\). Su interpretación como prueba MAP depende de un modelo con probabilidades a priori, pero su cálculo depende únicamente de\(p_0, p_1\) vistos como parámetros.
6. Una función convexa de una variable real a veces se define como una función con una segunda derivada no negativa, pero definirla como una función que se extiende sobre o sobre todas sus tangentes es más general, permitiendo discontinuidades escalonadas en la primera derivada de\( f\). Vemos en breve la necesidad de esta generalidad.
7. Si\(\text{p}_{\boldsymbol{Y} |H} (\boldsymbol{y} | 1) = 0\) y\(\text{p}_{\boldsymbol{Y} |H (\boldsymbol{y} | 0) > 0\) para algunos\(\boldsymbol{y}\), entonces\(\Lambda (\boldsymbol{y})\) es infinito, y por lo tanto defectuoso, condicionado\(H = 0\). Dado que el dado\(\boldsymbol{y}\) tiene probabilidad cero condicional\(H = 0\), vemos que no\(\Lambda (\boldsymbol{Y} )\) es defectuoso condicional on\(H = 1\).
8. En el caso discreto, puede haber múltiples soluciones a (7.3.8) para algunos valores de\(\alpha \), pero esto no afecta la regla de decisión. Se puede elegir el valor más pequeño de\(\eta \) a satisfacer (7.3.8) si se quiere eliminar esta ambigüedad.