10.4: Reconstrucción perfecta
- Page ID
- 86472
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introducción
Si ciertas suposiciones adicionales sobre la señal original y la frecuencia de muestreo se mantienen, entonces la señal original se puede recuperar exactamente de sus muestras usando un tipo de filtro particularmente importante. Más específicamente, se demostrará que si una señal de banda limitada es muestreada a una velocidad mayor al doble de su límite de banda, la fórmula de reconstrucción Whittaker-Shannon reconstruye perfectamente la señal original. Esta fórmula hace uso del filtro de paso bajo ideal, que está relacionado con la función sinc. Esto es extremadamente útil, ya que las versiones muestreadas de señales de tiempo continuas se pueden filtrar usando procesamiento de señal de tiempo discreto, a menudo en una computadora. Los resultados pueden entonces ser reconstruidos para producir la misma salida de tiempo continuo que algún sistema de tiempo continuo deseado.
Reconstrucción Perfecta
Para comprender las condiciones para una reconstrucción perfecta y el filtro que emplea, considere lo siguiente. Como inicio, se discutirá una condición suficiente bajo la cual es posible una reconstrucción perfecta. Posteriormente, se detallará el filtro y el proceso utilizado para una reconstrucción perfecta.
Recordemos que la versión muestreada\(x_s\) de una señal de tiempo continua\(x\) con periodo de muestreo\(T_s\) tiene un espectro dado por
\[X_{s}(\omega)=\frac{1}{T_{s}} \sum_{k=-\infty}^{\infty} X\left(\frac{\omega-2 \pi k}{T_{s}}\right). \nonumber \]
Como antes, tenga en cuenta que si\(x\) es banda limitada a\((−\pi /T_s, \pi /T_s)\), lo que significa que solo\(X\) es distinto de cero encendido\((−\pi /T_s, \pi /T_s)\), entonces cada periodo de\(X_s\) tiene la misma forma que\(X\). Así, podemos identificar el espectro original\(X\) a partir del espectro de las muestras\(X_s\) y, por extensión, la señal original\(x\) de sus muestras\(x_s\) a velocidad\(T_s\) si\(x\) está limitada en banda a\((−\pi /T_s, \pi /T_s)\).
Si una señal\(x\) está limitada en banda a\((−B,B)\), entonces también está limitada en banda a\((−\pi /T_s, \pi /T_s)\) siempre que eso\(T_s< \pi /B\). Por lo tanto, si nos aseguramos de que\(x\) se muestree\(x_s\) con una frecuencia angular de muestreo suficientemente alta\(\omega_s=2 \pi /T_s>2B\) y tenemos una manera de identificar la señal\((−\pi /T_s, \pi /T_s)\) limitada de banda única correspondiente a una señal de tiempo discreta en el período de muestreo\(T_s\), entonces se\(x_s\) puede usar para reconstruir \(\tilde{x}=x\)exactamente. La frecuencia\(2B\) se conoce como la velocidad angular de Nyquist. Por lo tanto, la condición de que la tasa de muestreo\(\omega_s=2 \pi /T_s>2B\) sea mayor que la tasa de Nyquist es una condición suficiente para que sea posible una reconstrucción perfecta.
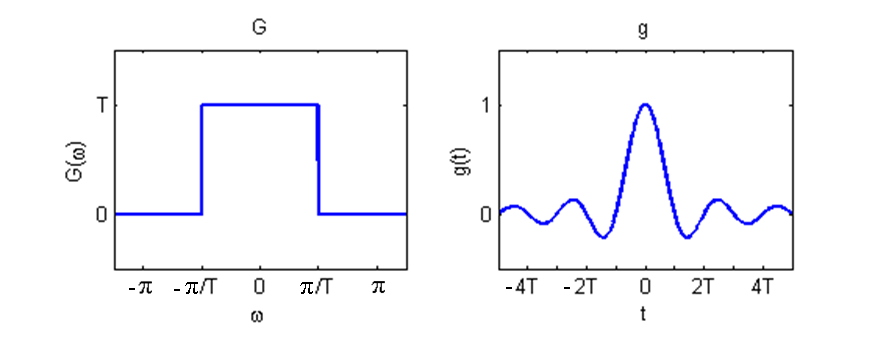
También se debe conocer el filtro correcto para poder realizar una reconstrucción perfecta. El filtro de paso bajo ideal definido por\(G(\omega)=T_s(u(\omega+\pi/T_s)−u(\omega−\pi/T_s))\), que se muestra en la Figura\(\PageIndex{1}\), elimina todo el contenido de señal que no está en el rango de frecuencia\((−\pi /T_s, \pi /T_s)\). Por lo tanto, la aplicación de este filtro al tren de impulsos\(\sum_{n=-\infty}^{\infty} x_{s}(n) \delta\left(t-n T_{s}\right)\) da como resultado una banda de salida limitada a\((−\pi /T_s, \pi /T_s)\).
Ahora solo necesitamos confirmar que la respuesta\(g\) de impulso del filtro\(G\) satisface nuestra condición suficiente para ser un filtro de reconstrucción. La transformada inversa de Fourier de\(G(\omega)\) es
\ [g (t) =\ nombreoperador {sinc}\ izquierda (t/T_ {s}\ derecha) =\ izquierda\ {\ begin {array} {cc}
1 & t=0\
\ frac {\ sin\ izquierda (\ pi t/T_ {s}\ derecha)} {\ pi t/T_ {s}} & t\ neq 0
\ end {array} derecha\.,\ nonumber\]
que se muestra en la Figura\(\PageIndex{6}\). Por lo tanto,
\ [g\ izquierda (n T_ {s}\ derecha) =\ nombreoperador {sinc} (n) =\ izquierda\ {\ comenzar {matriz} {cc}
1 & n=0\\
\ frac {\ sin (\ pi n)} {\ pi n} & n\ neq 0
\ end {array} =\ left\ {\ begin {array} {ll}
1 & n=0\
0 & n\ neq 0
\ end {array} =\ delta (n)\ derecha. \ derecho. \ nonumber\]
Por lo tanto, el filtro de paso bajo ideal\(G\) es un filtro de reconstrucción válido. Dado que es un filtro de reconstrucción válido y siempre produce una salida que está limitada en banda\((−\pi /T_s, \pi /T_s)\), este filtro siempre produce la señal de\((−\pi /T_s, \pi /T_s)\) banda limitada única que muestrea a una secuencia de tiempo discreta dada en el período de muestreo\(T_s\) cuando\(\sum_{n=-\infty}^{\infty} x_{s}(n) \delta\left(t-n T_{s}\right)\) se ingresa el tren de impulsos.
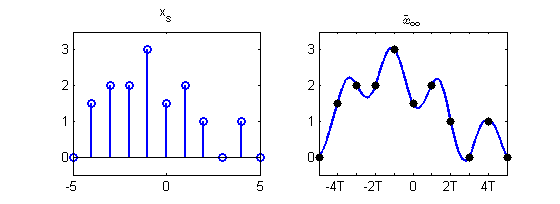
Por lo tanto, siempre podemos reconstruir cualquier señal de\((−\pi /T_s, \pi /T_s)\) banda limitada de sus muestras en el período de muestreo\(T_s\) mediante la fórmula
\[x(t)=\sum_{n=-\infty}^{\infty} x_{s}(n) \operatorname{sinc}\left(t / T_{s}-n\right). \nonumber \]
Esta fórmula de reconstrucción perfecta se conoce como la fórmula de interpolación Whittaker-Shannon y a veces también se llama la serie cardinal. De hecho, la función sinc es la spline de base cardinal de orden infinito\(\eta_{\infty}\). En consecuencia, el conjunto\(\left\{\operatorname{sinc}\left(t / T_{s}-n\right) \: | \: n \in \mathbb{Z}\right\}\) forma una base para el espacio vectorial de señales de\((−\pi /T_s, \pi /T_s)\) banda limitada donde las muestras de señal proporcionan los coeficientes correspondientes. Es un ejercicio sencillo para demostrar que esta base es, de hecho, una base ortogonal.
Resumen de Reconstrucción Perfecta
Este módulo ha demostrado que las señales de tiempo continuo de banda limitada pueden reconstruirse exactamente a partir de sus muestras siempre que la frecuencia de muestreo supere la tasa de Nyquist, que es el doble del límite de banda. La fórmula de reconstrucción Whittaker-Shannon computa esta reconstrucción perfecta usando un filtro de paso bajo ideal, siendo la señal resultante una suma de funciones sinc desplazadas que son escaladas por los valores de la muestra. El muestreo por debajo de la tasa de Nyquist puede conducir a un aliasing que hace que la señal original sea irrecuperable como se describe en el módulo posterior. La capacidad de reconstruir perfectamente señales de banda limitada tiene importantes implicaciones prácticas para el procesamiento de señales de tiempo continuas utilizando las herramientas de procesamiento de señal de tiempo discreto.


