11.1: Transformación de Laplace
- Page ID
- 86220
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introducción
La transformada de Laplace es una generalización de la Transformada de Fourier en Tiempo Continuo (Sección 8.2). Se usa porque el CTFT no converge/existe para muchas señales importantes, y sin embargo lo hace para la transformada Laplace (por ejemplo, señales con\(l_2\) norma infinita). También se utiliza porque es notacionaly más limpio que el CTFT. Sin embargo, en lugar de utilizar exponenciales complejos (Sección 7.2) de la forma\(e^{j \omega t}\), con parámetros puramente imaginarios, la transformada de Laplace utiliza lo más general\(e^{st}\), donde\(s=\sigma+j \omega\) es complejo, para analizar señales en términos de sinusoides ponderados exponencialmente.
La transformación de Laplace
Par de Transformación Bilateral Laplace
Aunque las transformaciones de Laplace rara vez se resuelven en la práctica usando integración (las tablas (Sección 11.2) y las computadoras (por ejemplo, Matlab) son mucho más comunes), proporcionaremos el par de transformaciones bilaterales de Laplace aquí para fines de discusión y derivación. Estos definen las transformaciones de Laplace hacia adelante e inversa. Observe las similitudes entre las transformaciones hacia adelante e inversa. Esto dará lugar a muchas de las mismas simetrías encontradas en el análisis de Fourier (Sección 5.1).
Transformación de Laplace
\[F(s)=\int_{-\infty}^{\infty} f(t) e^{-(s t)} d t \nonumber \]
Transformación inversa de Laplace
\[f(t)=\frac{1}{2 \pi j} \int_{c-j \infty}^{c+j \infty} F(s) e^{s t} d s \nonumber \]
Nota
Hemos definido la transformación bilateral de Laplace. También hay una transformación unilateral de Laplace,
\[F(s)=\int_{0}^{\infty} f(t) e^{-(s t)} \mathrm{d} t \nonumber \]
que es útil para resolver las ecuaciones de diferencia con condiciones iniciales distintas de cero. Esto es similar a la Transformada Z unilateral en Tiempo Discreto.
Relación entre Laplace y CTFT
Echando un vistazo a las ecuaciones que describen la Transformada Z y la Transformada de Fourier en Tiempo Discreto:
Transformada de Fourier en Tiempo Continuo
\[\mathcal{F}(\Omega)=\int_{-\infty}^{\infty} f(t) e^{-(j \Omega t)} d t \nonumber \]
Transformación de Laplace
\[F(s)=\int_{-\infty}^{\infty} f(t) e^{-(s t)} d t \nonumber \]
Podemos ver muchas similitudes; primero, que:
\[\mathcal{F}(\Omega)=F(s) \nonumber \]
para todos\(\Omega = s\).
Nota
El CTFT es una función de valor complejo de una variable de valor real\(\omega\) (y\(2\pi\) periódica). La transformada Z es una función de valor complejo de una variable z de valor complejo.
Parcelas
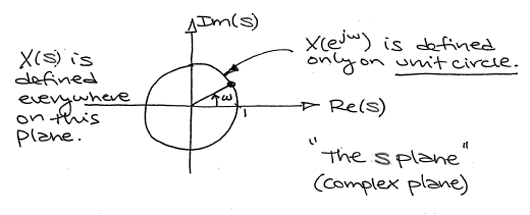
Figura\(\PageIndex{1}\)
Visualizando la Transformación de Laplace
Con la transformada de Fourier, tuvimos una función de valor complejo de una variable puramente imaginaria,\(F(j \omega)\). Esto era algo que podíamos imaginarnos con tramas bidimensionales (partes reales e imaginarias o magnitud y fase). Sin embargo, con Laplace, tenemos una función de valor complejo de una variable compleja. Para examinar la magnitud y fase o partes reales e imaginarias de esta función, debemos examinar las gráficas superficiales tridimensionales de cada componente.
Gráfica real e imaginaria
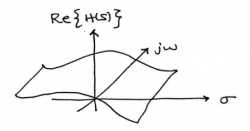
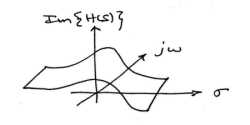
Gráfica de muestras de magnitud y fase
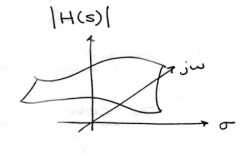
Si bien estas son formas legítimas de mirar una señal en el dominio de Laplace, es bastante difícil dibujar y/o analizar. Por esta razón, se ha desarrollado un método más sencillo. Aunque no se discutirá en detalle aquí, el método de Polos y Ceros es mucho más fácil de entender y es la forma en que tanto la transformación de Laplace como su contraparte de tiempo discreto, la transformada Z, se representan gráficamente.
Uso de una computadora para encontrar la transformación de Laplace
Usar una computadora para encontrar transformaciones de Laplace es relativamente indoloro. Matlab tiene dos funciones, laplace e ilaplace, que forman parte de la caja de herramientas simbólica, y encontrarán las transformaciones de Laplace e inversa de Laplace respectivamente. Este método es generalmente preferido para funciones más complicadas. Las funciones más simples y más ideadas generalmente se encuentran con bastante facilidad mediante el uso de tablas.
Demostración de definición de transformación de Laplace
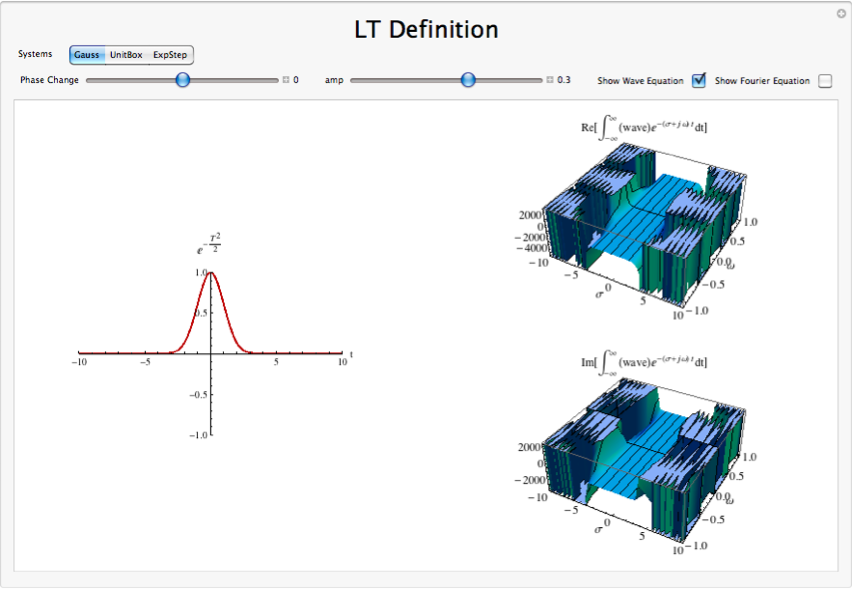
Demostraciones Interactivas
Conclusión
La transformada de laplace demuestra una forma útil y más general de la Transformada de Fourier de Tiempo Continuo. Se aplica igualmente bien a la descripción de sistemas, así como a las señales que utilizan el método de función propia, y a la descripción de una clase más grande de señales mejor descritas usando el método polo-cero.


