11.6: Región de Convergencia para la Transformación de Laplace
- Page ID
- 86236
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Con la transformada de Laplace (Sección 11.1), el plano s representa un conjunto de señales (exponenciales complejos (Sección 1.8)). Para cualquier sistema LTI (Sección 2.1) dado, algunas de estas señales pueden hacer que la salida del sistema converja, mientras que otras hacen que la salida diverja (“explote”). El conjunto de señales que hacen que la salida del sistema converja se encuentra en la región de convergencia (ROC). Este módulo discutirá cómo encontrar esta región de convergencia para cualquier sistema LTI de tiempo continuo.
Recordemos la definición de la transformación de Laplace,
Transformación de Laplace
\[H(s)=\int_{-\infty}^{\infty} h(t) e^{-(s t)} \mathrm{d} t \nonumber \]
Si consideramos un causal (Sección 1.1), exponencial complejo\(h(t)=e^{−(at)}u(t)\),, obtenemos la ecuación,
\[\int_{0}^{\infty} e^{-(a t)} e^{-(s t)} d t=\int_{0}^{\infty} e^{-((a+s) t)} d t \nonumber \]
Evaluando esto, obtenemos
\[\frac{-1}{s+a}\left(\lim_{t \rightarrow \infty} e^{-((s+a) t)}-1\right) \nonumber \]
Observe que esta ecuación tenderá al infinito cuando\(\lim_{t \rightarrow \infty} e^{-((s+a) t)}\) tiende al infinito. Para entender cuando esto sucede, damos un paso más usando\(s=\sigma+j \omega\) para realizar esta ecuación como
\[\lim_{t \rightarrow \infty} e^{-(j \omega t)} e^{-((\sigma+a) t)} \nonumber \]
Al reconocer que\(e^{−(j \omega t)}\) es sinusoidal, se hace evidente que\(e^{−(\sigma (a)t)}\) va a determinar si esto explota o no. Lo que encontramos es que si\(\sigma + a\) es positivo, lo exponencial será a una potencia negativa, lo que provocará que vaya a cero ya que tt tiende al infinito. Por otro lado, si σ+aσ a es negativo o cero, lo exponencial no será a una potencia negativa, lo que evitará que tienda a cero y el sistema no convergerá. Lo que todo esto nos dice es que para una señal causal, tenemos convergencia cuando
Condición para Convergencia
\[\operatorname{Re}(s)>-a \nonumber \]
Aunque no volveremos a pasar por el proceso por señales anticausales, podríamos. Al hacerlo, encontraríamos que la condición necesaria para la convergencia es cuando
Condición necesaria para la convergencia anticausal
\[\operatorname{Re}(s)<-a \nonumber \]
Comprensión gráfica de ROC
Quizás la mejor manera de ver la región de convergencia es verla en el plano s. Lo que observamos es que para un solo polo, la región de convergencia se encuentra a su derecha para señales causales y a la izquierda para señales anticausales.
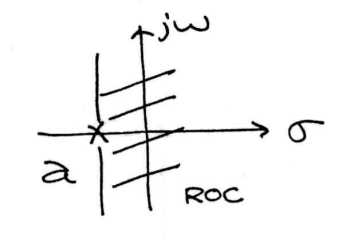 a) La Región de Convergencia para una señal causal.
a) La Región de Convergencia para una señal causal. 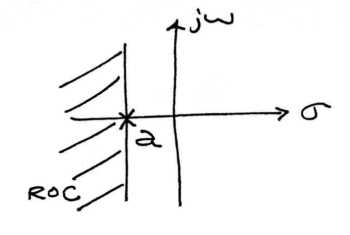 b) La Región de Convergencia para una señal anticausal.
b) La Región de Convergencia para una señal anticausal.
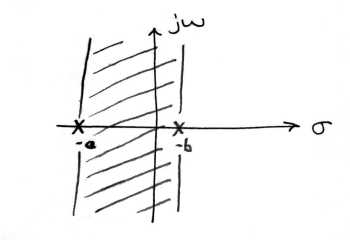
Una vez que lo hemos reconocido, la pregunta natural se convierte en: ¿Qué hacemos cuando tenemos múltiples polos? La respuesta simple es que tomamos la intersección de todas las regiones de convergencia de los polos respectivos.
Ejemplo\(\PageIndex{1}\)
Encontrar\(H(s)\) y declarar la región de convergencia para\(h(t)=e^{-(a t)} u(t)+e^{-(b t)} u(-t)\)
Rompiendo esto en sus dos términos, obtenemos funciones de transferencia y respectivas regiones de convergencia de
\ [\ begin {array} {l}
H_ {1} (s) =\ frac {1} {s+a},\:\ nombreoperador {Re} (s) >-a\\
H_ {2} (s) =\ frac {-1} {s+b},\:\ nombreoperador {Re} (s) <-b
\ end {array}\ nonumber\]
\(-b>\operatorname{Re}(s)>-a\). Si\(a>b\), podemos representar esto gráficamente. De lo contrario, no habrá región de convergencia.