11.9: Diseño de Filtro de Tiempo Continuo
- Page ID
- 86192
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introducción
Los filtros analógicos (Continuous-Time) son útiles para una amplia variedad de aplicaciones, y son especialmente útiles porque son muy simples de construir usando componentes estándar, pasivos R, L, C. Tener una conexión a tierra en la teoría básica del diseño de filtros puede ayudar a uno a resolver una amplia variedad de problemas de procesamiento de señales.
Estimación de la respuesta de frecuencia desde el plano Z
Uno de los factores motivadores para analizar las parcelas polo/cero se debe a su relación con la respuesta de frecuencia del sistema. Con base en la posición de los polos y ceros, se puede determinar rápidamente la respuesta de frecuencia. Esto es resultado de la correspondencia entre la respuesta de frecuencia y la función de transferencia evaluada en el círculo unitario en las gráficas polo/cero. La respuesta de frecuencia, o DTFT, del sistema se define como:
\ [\ begin {alineado}
H (w) &=\ izquierda.h (z)\ derecha|_ {z, z=e^ {j w}}\\ [4pt]
&=\ frac {\ displaystyle\ sum_ {k=0} ^ {M} b_ {k} e^ {- (j w k)}} {\ displaystyle\ sum_ {k=0} ^ {^ N} a_ {k} e^ {- (j w k)}}
\ final {alineado}\ nonumber\]
A continuación, al factorizar la función de transferencia en polos y ceros y multiplicar el numerador y el denominador por\(e^{jw}\) llegamos a las siguientes ecuaciones:
\[H(w)=\left|\frac{b_{0}}{a_{0}}\right| \frac{\displaystyle\prod_{k=1}^{M}\left|e^{j w}-c_{k}\right|}{\displaystyle\prod_{k=1}^{N}\left|e^{j w}-d_{k}\right|} \label{11.50} \]
De la Ecuación\ ref {11.50} tenemos la respuesta de frecuencia en una forma que puede ser utilizada para interpretar características físicas sobre la respuesta de frecuencia del filtro. El numerador y denominador contienen un producto de términos de la forma\(\left|e^{j w}-h\right|\), donde\(h\) es un cero, denotado por\(c_k\) o un polo, denotado por\(d_k\). Los vectores se utilizan comúnmente para representar el término y sus partes en el plano complejo. El polo o cero,\(h\), es un vector desde el origen hasta su ubicación en cualquier parte del plano complejo y\(e^{jw}\) es un vector desde el origen hasta su ubicación en el círculo unitario. El vector que conecta estos dos puntos\(\left|e^{j w}-h\right|\),, conecta el polo o ubicación cero a un lugar en el círculo unitario dependiendo del valor de\(w\). A partir de esto, podemos comenzar a entender cómo la magnitud de la respuesta de frecuencia es una relación de las distancias a los polos y cero presente en el plano z como\(w\) va de cero a pi. Estas características nos permiten interpretar de la\(|H(w)|\) siguiente manera:
\[|H(w)|=\left|\frac{b_{0}}{a_{0}}\right| \frac{\displaystyle\prod \text { "distances from zeros" }}{\displaystyle\prod \text { "distances from poles" }} \nonumber \]
En conclusión, utilizando las distancias desde el círculo unitario hasta los polos y ceros, podemos trazar la respuesta de frecuencia del sistema. Como\(w\) va de\(0\) a\(2 \pi\), las dos propiedades siguientes, tomadas de las ecuaciones anteriores, especifican cómo se debe dibujar\(|H(w)|\).
Mientras se mueve alrededor del círculo de la unidad...
- Si está cerca de un cero, entonces la magnitud es pequeña. Si hay un cero en el círculo unitario, entonces la respuesta de frecuencia es cero en ese punto.
- Si está cerca de un polo, entonces la magnitud es grande. Si un polo está en el círculo unitario, entonces la respuesta de frecuencia va al infinito en ese punto.
Respuesta de frecuencia de dibujo desde la gráfica de polo/cero
Veamos ahora varios ejemplos de determinación de la magnitud de la respuesta de frecuencia a partir de la gráfica polo/cero de una transformada z. Si ha olvidado o no está familiarizado con las parcelas polo/cero, consulte el módulo Polo/Zero Plot (Sección 12.5).
Ejemplo\(\PageIndex{1}\)
En este primer ejemplo vamos a echar un vistazo a la muy simple z-transform que se muestra a continuación:
\[H(z)=z+1=1+z^{−1} \nonumber \]
\[H(w)=1+e^{−(jw)} \nonumber \]
Para este ejemplo, algunos de los vectores representados por\(\left|e^{j w}-h\right|\), para valores aleatorios de\(w\), se dibujan explícitamente sobre el plano complejo que se muestra en la siguiente figura. Estos vectores muestran cómo cambia la amplitud de la respuesta de frecuencia a medida que ww va de 00 a 2π2, y también muestran el significado físico de los términos en la Ecuación\ ref {11.50} anterior. Se puede ver que cuando\(w=0\), el vector es el más largo y así la respuesta de frecuencia tendrá aquí su mayor amplitud. A medida que\(w\) se aproxima\(\pi\), la longitud de los vectores disminuye al igual que la amplitud de\(|H(w)|\). Como no hay polos en la transformada, solo existe este término de un vector en lugar de una relación como se ve en la Ecuación\ ref {11.50}.


Ejemplo\(\PageIndex{2}\)
Para este ejemplo, se analiza una función de transferencia más compleja para representar la respuesta de frecuencia del sistema.
\[H(z)=\frac{z}{z-\frac{1}{2}}=\frac{1}{1-\frac{1}{2} z^{-1}} \nonumber \]
\[H(w)=\frac{1}{1-\frac{1}{2} e^{-(j w)}} \nonumber \]
A continuación podemos ver las dos figuras descritas por las ecuaciones anteriores. La Figura\(\PageIndex{2(a)}\) representa la gráfica básica polo/cero de la transformada z,\(H(w)\). La figura\(\PageIndex{2(b)}\) muestra la magnitud de la respuesta de frecuencia. A partir de las fórmulas y declaraciones de la sección anterior, podemos ver que cuando\(w=0\) la frecuencia alcanzará su pico ya que está en este valor de\(w\) que el polo está más cerca del círculo unitario. La relación de Ecuación\ ref {11.50} nos ayuda a ver las matemáticas detrás de esta conclusión y la relación entre las distancias del círculo unitario y los polos y ceros. A medida que\(w\) se mueve de\(0\) a\(\pi\), vemos cómo el cero comienza a enmascarar los efectos del polo y así forzar la respuesta de frecuencia más cerca a\(0\).
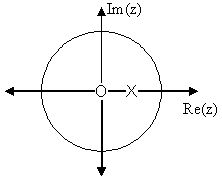


Tipos de Filtros
Filtros Butterworth
El filtro Butterworth es el filtro más simple. Se puede construir a partir de circuitos pasivos R, L, C. La magnitud de la función de transferencia para este filtro es
Magnitud de la función de transferencia de filtro But
\[|H(j \omega)|=\frac{1}{\sqrt{1+\left(\frac{\omega}{\omega_{c}}\right)^{2 n}}} \nonumber \]
donde\(n\) es el orden del filtro y\(\omega_c\) es la frecuencia de corte. La frecuencia de corte es la frecuencia donde la magnitud experimenta una caída de 3 dB (donde\(|H(j \omega)|=\frac{1}{\sqrt{2}}\)).
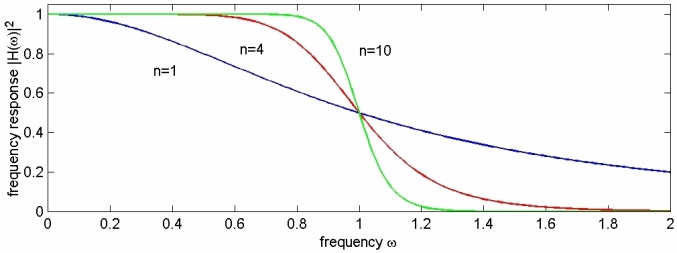
Los aspectos importantes de la Figura\(\PageIndex{3}\) son que no ondulan en la banda de paso o stopband como tienden a hacerlo otros filtros, y que cuanto mayor nn, más nítido es el corte (cuanto menor es la banda de transición).
Los filtros Butterworth dan funciones de transferencia\((H(j \omega)\) y\(H(s)\)) que son funciones racionales. También tienen solo polos, lo que resulta en una función de transferencia de la forma
\[\frac{1}{\left(s-s_{1}\right)\left(s-s_{2}\right) \cdots\left(s-s_{n}\right)} \nonumber \]
y una gráfica polo-cero de
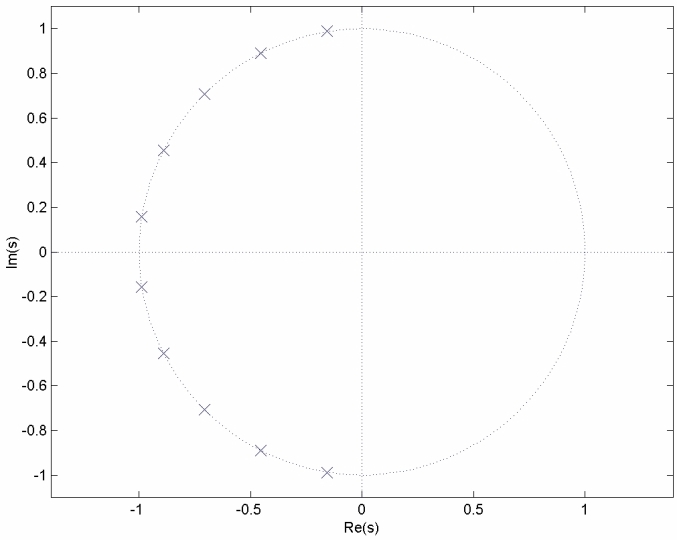
Tenga en cuenta que los polos se encuentran a lo largo de un círculo en el plano s.
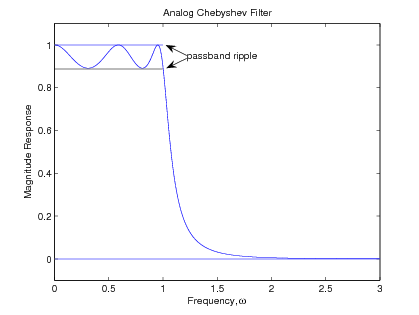
Filtros Chebyshev
El filtro Butterworth no da una aproximación suficientemente buena a través de la banda de paso completa en muchos casos. La aproximación de la serie de Taylor a menudo no es adecuada para la forma en que se dan las especificaciones para los filtros. Una medida de error alternativa es el máximo del valor absoluto de la diferencia entre la respuesta de filtro real y la ideal. Esto se considera sobre la banda de paso total. Esta es la medida de error de Chebyshev y se definió y aplicó al problema de diseño del filtro FIR. Para el filtro IIR, el error de Chebyshev se minimiza sobre la banda de paso y\(\omega = \infty\) se utiliza una aproximación de la serie de Taylor en para determinar el rendimiento de la banda de parada. Esta mezcla de métodos en el caso IIR se llama filtro Chebyshev, y resultan fórmulas de diseño simples, al igual que para el filtro Butterworth.
El diseño de los filtros de Chebyshev es particularmente interesante, porque los resultados de una teoría muy elegante aseguran que construir una función de frecuencia-respuesta con la forma adecuada de ondulación igual en el error dará como resultado un error mínimo de Chebyshev sin minimizar explícitamente nada. Esto permite derivar un conjunto sencillo de fórmulas de diseño que pueden verse como una generalización de las fórmulas de Butterworth.
La forma para la magnitud al cuadrado de la función frecuencia-respuesta para el filtro Chebyshev es
\[|F(j \omega)|^{2}=\frac{1}{1+\epsilon^{2} C_{N}(\omega)^{2}} \label{11.54} \]
donde\(C_N(\omega)\) es un polinomio Chebyshev de orden N y\(\epsilon\) es un parámetro que controla el tamaño de ondulación. Este polinomio\(\omega\) tiene características muy especiales que dan como resultado la optimalidad de la función de respuesta (Ecuación\ ref {11.54}).
Filtros Bessel
Insertar información de filtro bessel
Filtros Elípticos
Hay otro método que se ha desarrollado que utiliza un criterio de error de Chebyshev tanto en la banda de paso como en la banda de parada. Esta es la cuarta combinación posible de aproximaciones de las series de Chebyshev y Taylor en la banda de paso y la banda de parada. El filtro resultante se llama filtro de función elíptica, ya que las funciones elípticas se utilizan normalmente para calcular las ubicaciones de polo y cero. También se le llama a veces un filtro Cauer o un filtro Chebyshev racional, y tiene igual error de aproximación de ondulación tanto en las bandas de paso como de parada.
Los criterios de error del filtro de función elíptica son particularmente adecuados para la forma en que a menudo se dan las especificaciones para los filtros. Por esa razón, el uso del diseño del filtro de función elíptica generalmente da el filtro de orden más bajo de los cuatro métodos clásicos de diseño de filtro para un conjunto dado de especificaciones. Desafortunadamente, el diseño de este filtro es el más complicado de los cuatro. Sin embargo, debido a la eficiencia de esta clase de filtros, vale la pena obtener alguna comprensión de las matemáticas detrás del procedimiento de diseño.
Esta sección esboza un esquema de la teoría del diseño de filtros de función elíptica. Los detalles y propiedades de las funciones elípticas en sí mismas simplemente deben ser aceptados, y poner la atención en comprender el panorama general. Un desarrollo más completo está disponible en.
Debido a que tanto las aproximaciones de banda de paso como de banda de parada están en todas las bandas, se debe definir una banda de transición entre las dos. Usando un borde de banda de paso normalizado, las bandas se definen por
\ [\ begin {array} {c}
0<\ omega<1\ quad\ text {passband}\\
1<\ omega<\ omega_ {s}\ quad\ text {banda de transición}\
\ omega_ {s} <\ omega<\ infty\ quad\ text {stopband}
\ end {array}\ nonumber\]
Esto se ilustra en la Figura\(\PageIndex{6}\).
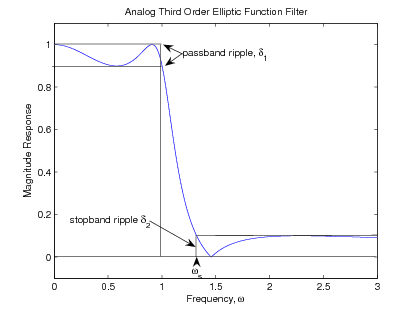
Las características del filtro de función elíptica se describen mejor en términos de los cuatro parámetros que especifican la respuesta de frecuencia:
- La variación o ondulación máxima en la banda de paso\(\delta_{1}\),
- El ancho de la banda de transición\((\omega_s−1)\),
- La respuesta máxima o ondulación en la banda de detención\(\delta_2\), y
- El orden del filtro\(N\).
El resultado del diseño es que para cualquiera de los tres parámetros dados, el cuarto es mínimo. Esta es una descripción muy flexible y potente de una respuesta de frecuencia de filtro.
La forma de la función frecuencia-respuesta es una generalización de la del filtro Chebyshev
\[F F(j \omega)=|F(j \omega)|^{2}=\frac{1}{1+\epsilon^{2} G^{2}(\omega)} \nonumber \]
donde
\[F F(s)=F(s) F(-s) \nonumber \]
\(F(s)\)siendo el prototipo de función de transferencia de filtro analógico similar a la del filtro Chebyshev. \(G(\omega)\)es una función racional que se aproxima a cero en la banda de paso e infinito en la banda de parada. La definición de esta función es una generalización de la definición del polinomio Chebyshev.
Demostración de diseño de filtros
Conclusión
Como se puede ver, hay una gran cantidad de información disponible en el diseño de filtros, más de lo que puede cubrir un módulo introductorio. Incluso para diseñar filtros IIR de tiempo discreto, es importante recordar que existe un cuerpo de literatura mucho más grande para los métodos de diseño para el mundo del procesamiento de señales analógicas que para el digital. Por lo tanto, a menudo es más fácil y práctico implementar un filtro IIR utilizando métodos analógicos estándar, y luego discretizarlo usando métodos como la Transformación Bilateral.


