12.1: Transformación Z
- Page ID
- 86364
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introducción
La transformada Z es una generalización de la Transformada de Fourier de Tiempo Discreto (Sección 9.2). Se utiliza porque el DTFT no converge/existe para muchas señales importantes, y sin embargo lo hace para la transformada z. También se usa porque es notacionalmente más limpio que el DTFT. En contraste con el DTFT, en lugar de usar exponenciales complejos (Sección 7.2) de la forma (e^ {j\ omega n}\), con parámetros puramente imaginarios, la transformada Z utiliza el más general,\(z^n\), donde\(z\) es complejo. Por lo tanto, la transformada Z permite incorporar el poder de la teoría de variables complejas al procesamiento de señales digitales.
La transformación Z
Par Bilateral de Transformación Z
Aunque las transformaciones Z rara vez se resuelven en la práctica usando integración (tablas y computadoras (por ejemplo, Matlab) son mucho más comunes), proporcionaremos el par de transformaciones Z bilaterales aquí para fines de discusión y derivación. Estos definen las transformaciones Z hacia adelante e inversa. Observe las similitudes entre las transformaciones hacia adelante e inversa. Esto dará lugar a muchas de las mismas simetrías encontradas en el análisis de Fourier (Sección 5.1).
Transformación Z
\[X(z)=\sum_{n=-\infty}^{\infty} x[n] z^{-n} \nonumber \]
Transformación Z inversa
\[x[n]=\frac{1}{2 \pi j} \oint_{r} X(z) z^{n-1} \mathrm{d} z \nonumber \]
Nota
Hemos definido la transformada z bilateral. También hay una transformación z unilateral,
\[X(z)=\sum_{n=0}^{\infty} x[n] z^{-n} \nonumber \]
que es útil para resolver las ecuaciones de diferencia con condiciones iniciales distintas de cero. Esto es similar a la Transformación unilateral de Laplace en tiempo continuo.
Relación entre transformada Z y DTFT
Echando un vistazo a las ecuaciones que describen la Transformada Z y la Transformada de Fourier en Tiempo Discreto:
Transformada de Fourier en Tiempo Discreto
\[X\left(e^{j \omega}\right)=\sum_{n=-\infty}^{\infty} x(n) e^{-(j \omega n)} \nonumber \]
Transformación Z
\[X(z)=\sum_{n=-\infty}^{\infty} x[n] z^{-n} \nonumber \]
Podemos ver muchas similitudes; primero, que:
\[X\left(e^{j \omega}\right)=X(z) \nonumber \]
para todos\(z=e^{j \omega}\)
Visualización de la transformada Z
Con el DTFT, tenemos una función de valor complejo de una variable de valor real\(\omega\) (y\(2\pi\) periódica). La transformada Z es una función de valor complejo de una variable z de valor complejo.
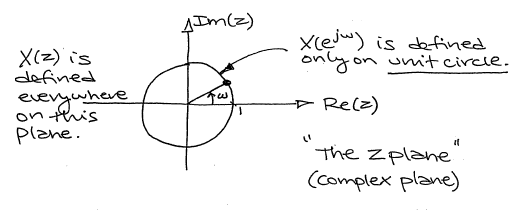
Figura\(\PageIndex{1}\)
Con la transformada de Fourier, tuvimos una función de valor complejo de una variable puramente imaginaria,\(F(j \omega)\). Esto era algo que podíamos imaginar con tramas bidimensionales (partes reales e imaginarias o magnitud y fase). Sin embargo, con Z, tenemos una función de valor complejo de una variable compleja. Para examinar la magnitud y fase o partes reales e imaginarias de esta función, debemos examinar las gráficas superficiales tridimensionales de cada componente.
Considere la transformada z dada por\(H(z)=z\), como se ilustra a continuación.
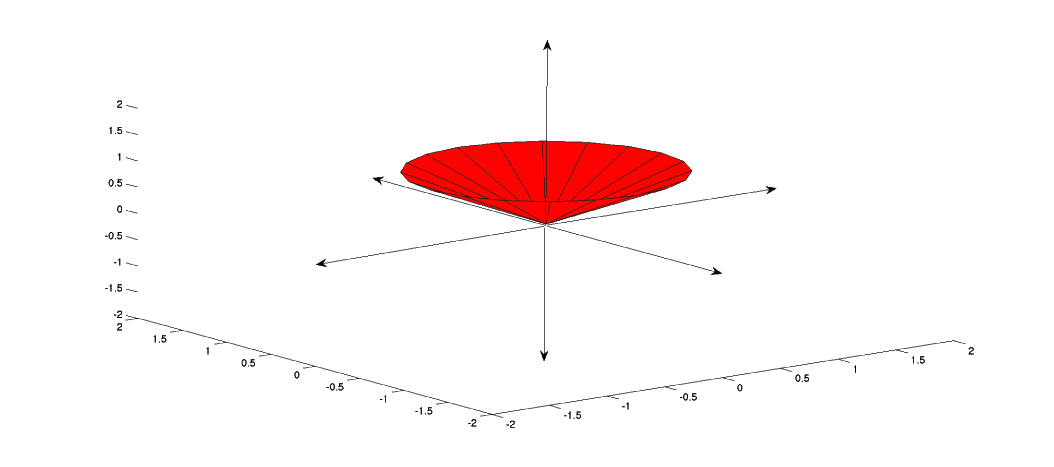
Figura\(\PageIndex{2}\)
El DTFT correspondiente tiene magnitud y fase que se dan a continuación.
Nota
Si bien estas son formas legítimas de mirar una señal en el dominio Z, es bastante difícil de dibujar y/o analizar. Por ello, se ha desarrollado un método más sencillo. Aunque no se discutirá en detalle aquí, el método de Polos y Ceros es mucho más fácil de entender y es la forma en que se representan gráficamente tanto la transformación Z como su contraparte de tiempo continuo la transformada Laplace.
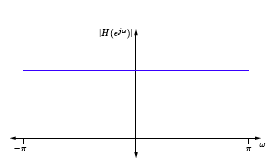
(a)
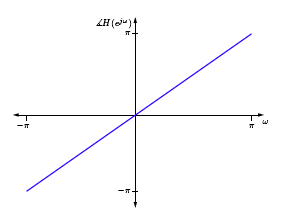
b)
¿Qué podría estar haciendo el sistema H? Es un sistema perfecto de fase lineal de paso completo. Pero, ¿qué significa esto?
Supongamos\(h[n]=\delta\left[n-n_{0}\right]\). Entonces
\ [\ begin {alineado}
H (z) &=\ sum_ {n=-\ infty} ^ {\ infty} h [n] z^ {-n}\\
&=\ sum_ {n=-\ infty} ^ {\ infty}\ delta\ izquierda [n-n_ {0}\ derecha] z^ {-n}\\
&=z^ {-n_ {0}}
\ end {alineado}\ nonumber\]
Así,\(H(z)=z^{−n_0}\) es la\(z\) -transformada de un sistema que simplemente retrasa la entrada por\(n_0\). \(H(z)\)es la\(z\) -transformada de un retardo de unidad.
Ahora considere\(x[n]=\alpha^{n} u[n]\)
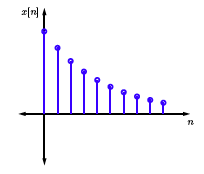
Figura\(\PageIndex{4}\)
\ [\ begin {align}
X (z) &=\ suma_ {n=-\ infty} ^ {\ infty} x [n] z^ {-n} =\ suma_ {n=0} ^ {\ infty}\ alfa^ {n} z^ {-n}\ nonumber\\
&=\ sum_ {n=0} ^ {\ infty}\ izquierda (\ frac {\ alfa} {z}\ derecha) ^ {n}\ nonumber\\
&=\ frac {1} {1-\ frac {\ frac {\ alpha} {z}}\ left (\ text {if}\ izquierda|\ frac {\ alpha} {z}\ derecha| <1\ derecha) (\ texto {Serie geométrica})\ nonumber\\
&=\ frac {z} {z-\ alpha}
\ end {align}\ nonumber\]
¿Y si\(|\frac{\alpha}{z}|≥1\)? ¡Entonces\(\sum_{n=0}^{\infty}\left(\frac{\alpha}{z}\right)^{n}\) no converge! Por lo tanto, siempre que calculemos un\(z\) -tranform, también debemos especificar el conjunto de\(z\)'s para el que existe la\(z\) -transform. A esto se le llama la región de convergencia (ROC).
Nota: Usar una computadora para encontrar la transformada Z
Matlab tiene dos funciones,
ztrans
y
iztrans
que forman parte de la caja de herramientas simbólica, y encontrarán las transformaciones Z e inversas Z respectivamente. Este método es generalmente preferido para funciones más complicadas. Las funciones más simples y más elaboradas generalmente se encuentran con bastante facilidad mediante el uso de tablas.
Aplicación a filtros de tiempo discretos
El\(z\) -transform puede parecer un poco feo. Tenemos que preocuparnos por la región de convergencia, y los temas de estabilidad, y así sucesivamente. No obstante, al final vale la pena porque resulta sumamente útil en el análisis de filtros digitales con retroalimentación. Por ejemplo, considere el sistema ilustrado a continuación
Parcelas
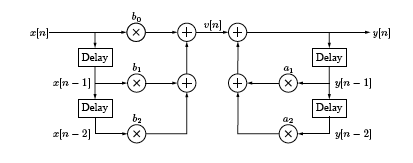
Figura\(\PageIndex{5}\)
Podemos analizar este sistema a través de las ecuaciones
\[v[n]=b_{0} x[n]+b_{1} x[n-1]+b_{2} x[n-2] \nonumber \]
y
\[y[n]=v[n]+a_{1} y[n-1]+a_{2} y[n-2] \nonumber \]
De manera más general,
\[v[n]=\sum_{k=0}^{N} b_{k} x[n-k] \nonumber \]
y
\[y[n]=\sum_{k=1}^{M} a_{k} y[n-k]+v[n] \nonumber \]
o equivalentemente,
\[\sum_{k=0}^{N} b_{k} x[n-k]=y[n]-\sum_{k=1}^{M} a_{k} y[n-k]. \nonumber \]
¿Cómo se ve la\(z\) transformación de esta relación?
\[Z \sum_{k=0}^{M} a_{k} y[n-k]=Z \sum_{k=0}^{M} b_{k} x[n-k] \nonumber \]
\[\sum_{k=0}^{M} a_{k} Z\{y[n-k]\}=\sum_{k=0}^{M} b_{k} Z\{x[n-k]\} \nonumber \]
Tenga en cuenta que
\ [\ begin {alineado}
Z\ {y [n-k]\} &=\ sum_ {n=-\ infty} ^ {\ infty} y [n-k] z^ {-n}\\
&=\ sum_ {m=-\ infty} ^ {\ infty} y [m] z^ {-m} z^ {-m} z^ {-k}\\
&=Y (z) z^ {-k}
\ final {alineado}\ nonumber\]
Así la relación se reduce a
\ begin {alineado}
\ sum_ {k=0} ^ {M} a_ {k} Y (z) z^ {-k} &=\ sum_ {k=0} ^ {N} b_ {k} X (z) z^ {-k}\\
Y (z)\ sum_ {k=0} ^ {M} a_ {k} z^ {-k} &=X (z)\ suma_ {k=0} ^ {N} b_ {k} z^ {-k}\
\ frac {Y (z)} {X (z)} &=\ frac {\ suma_ {k=0} ^ {N} b_ {k} z^ {-k}} {\ suma_ {k=0} ^ {M} a_ {k} z^ {-k} k}}
\ end {alineado}
Por lo tanto, dado un sistema el anterior, podemos determinar fácilmente la función de transferencia del sistema, y terminar con una relación de dos polinomios en\(z\): una función racional. Del mismo modo, dada una función racional, es fácil realizar esta función en una arquitectura de hardware simple.
Demostración interactiva de transformación Z
Conclusión
La transformada z demuestra una forma útil y más general de la Transformada Discreta de Fourier de Tiempo. Se aplica igualmente bien a la descripción de sistemas, así como a señales que utilizan el método de función propia, y resulta extremadamente útil en el diseño de filtros digitales.


