12.9: Diseño de Filtro de Tiempo Discreto
- Page ID
- 86424
Estimación de la respuesta de frecuencia desde el plano Z
Uno de los principales factores motivadores para utilizar la transformada z y analizar las gráficas polo/cero se debe a su relación con la respuesta de frecuencia de un sistema de tiempo discreto. Con base en la posición de los polos y ceros, se puede determinar rápidamente la respuesta de frecuencia. Esto es resultado de la correspondencia entre la respuesta de frecuencia y la función de transferencia evaluada en el círculo unitario en las gráficas polo/cero. La respuesta de frecuencia, o DTFT, del sistema se define como:
\ [\ begin {align}
H (w) &=\ izquierda.h (z)\ derecha|_ {z, z=e^ {j w}}\ nonumber\\
&=\ frac {\ sum_ {k=0} ^ {M} b_ {k} e^ {- (jwk)}} {\ sum_ {k=0} ^ {N} a_} e^ {- (jw k)}}
\ end {align}\ nonumber\]
A continuación, al factorizar la función de transferencia en polos y ceros y multiplicar el numerador y el denominador por\(e^{jw}\) llegamos a las siguientes ecuaciones:
\[H(w)=\left|\frac{b_{0}}{a_{0}}\right| \frac{\prod_{k=1}^{M}\left|e^{j w}-c_{k}\right|}{\prod_{k=1}^{N}\left|e^{j w}-d_{k}\right|} \label{12.80} \]
De la Ecuación\ ref {12.80} tenemos la respuesta de frecuencia en una forma que puede ser utilizada para interpretar características físicas sobre la respuesta de frecuencia del filtro. El numerador y denominador contienen un producto de términos de la forma\(|e^{jw}-h|\), donde\(h\) es un cero, denotado por\(c_k\) o un polo, denotado por\(d_k\). Los vectores se utilizan comúnmente para representar el término y sus partes en el plano complejo. El polo o cero,\(h\), es un vector desde el origen hasta su ubicación en cualquier parte del plano complejo y\(e^{jw}\) es un vector desde el origen hasta su ubicación en el círculo unitario. El vector que conecta estos dos puntos\(|e^{jw}-h|\),, conecta el polo o ubicación cero a un lugar en el círculo unitario dependiendo del valor de\(w\). A partir de esto, podemos comenzar a entender cómo la magnitud de la respuesta de frecuencia es una relación de las distancias a los polos y cero presente en el plano z a medida que ww va de cero a pi. Estas características nos permiten interpretar de la\(|H(w)|\) siguiente manera:
\[|H(w)|=\left|\frac{b_{0}}{a_{0}}\right| \frac{\prod \text { "distances from zeros" }}{\prod \text { "distances from poles" }} \nonumber \]
Respuesta de frecuencia de dibujo desde la gráfica de polo/cero
Veamos ahora varios ejemplos de determinación de la magnitud de la respuesta de frecuencia a partir de la gráfica polo/cero de una transformada z. Si ha olvidado o no está familiarizado con las parcelas polo/cero, consulte el módulo Polo/Zero Plot (Sección 12.5).
Ejemplo\(\PageIndex{1}\)
En este primer ejemplo vamos a echar un vistazo a la muy simple z-transform que se muestra a continuación:
\[H(z)=z+1=1+z^{-1} \nonumber \]
\[H(w)=1+e^{-(j w)} \nonumber \]
Para este ejemplo, algunos de los vectores representados por\(\left|e^{j w}-h\right|\), para valores aleatorios de\(w\), se dibujan explícitamente sobre el plano complejo que se muestra en la Figura\(\PageIndex{1}\) siguiente. Estos vectores muestran cómo la amplitud de la respuesta de frecuencia cambia a medida que\(w\) va de\(0\) a\(2 \pi\), y también muestran el significado físico de los términos en la Ecuación\ ref {12.80} anterior. Se puede ver que cuando\(w=0\), el vector es el más largo y así la respuesta de frecuencia tendrá aquí su mayor amplitud. A medida que se acerca ww\(\pi\), la longitud de los vectores disminuye al igual que la amplitud de\(|H(w)|\). Como no hay polos en la transformada, solo existe este término de un vector en lugar de una relación como se ve en la Ecuación\ ref {12.80}.
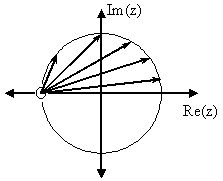
(a) Parcela Polo/Cero
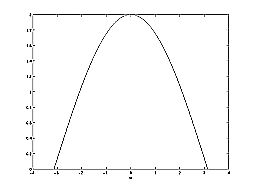
b) Respuesta de frecuencia:\(|H(w)|\)
Ejemplo\(\PageIndex{2}\)
Para este ejemplo, se analiza una función de transferencia más compleja para representar la respuesta de frecuencia del sistema.
\[H(z)=\frac{z}{z-\frac{1}{2}}=\frac{1}{1-\frac{1}{2} z^{-1}} \nonumber \]
\[H(w)=\frac{1}{1-\frac{1}{2} e^{-(j w)}} \nonumber \]
A continuación podemos ver las dos figuras descritas por las ecuaciones anteriores. La Figura\(\PageIndex{2}(a)\) representa la gráfica básica polo/cero de la transformada z,\(H(w)\). La figura\(\PageIndex{2}(b)\) muestra la magnitud de la respuesta de frecuencia. A partir de las fórmulas y declaraciones de la sección anterior, podemos ver que cuando\(w=0\) la frecuencia alcanzará su pico ya que es a este valor de ww donde el polo está más cercano al círculo unitario. La relación de Ecuación\ ref {12.80} nos ayuda a ver las matemáticas detrás de esta conclusión y la relación entre las distancias del círculo unitario y los polos y ceros. A medida que\(w\) se mueve de\(0\) a\(\pi\), vemos cómo el cero comienza a enmascarar los efectos del polo y así forzar la respuesta de frecuencia más cerca a\(0\).
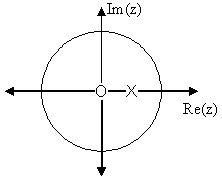
(a) Parcela Polo/Cero
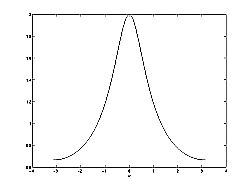
b) Respuesta de frecuencia:\(|H(w)|\)
Diseño de Filtros Interactivos Ilustración
Conclusión
En conclusión, utilizando las distancias desde el círculo unitario hasta los polos y ceros, podemos trazar la respuesta de frecuencia del sistema. A medida que ww va de\(0\) a\(2\pi\), las dos propiedades siguientes, tomadas de las ecuaciones anteriores, especifican cómo se debe dibujar\(|H(w)|\).
Mientras se mueve alrededor del círculo de la unidad...
- si está cerca de un cero, entonces la magnitud es pequeña. Si hay un cero en el círculo unitario, entonces la respuesta de frecuencia es cero en ese punto.
- si está cerca de un polo, entonces la magnitud es grande. Si un polo está en el círculo unitario, entonces la respuesta de frecuencia va al infinito en ese punto.