15.7: Espacios comunes de Hilbert
- Page ID
- 86596
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Espacios comunes de Hilbert
A continuación veremos los cuatro espacios Hilbert más comunes (Sección 15.4) con los que tendrá que lidiar al discutir y manipular señales y sistemas.
\(\mathbb{R}^n\)(escalares reales) y\(\mathbb{C}^n\) (escalares complejos), también llamados\(\ell^{2}([0, n-1])\)
\ (\ negridsymbol {x} =\ left (\ begin {array} {c}
x_ {0}\\
x_ {1}\\
\ puntos\\
x_ {n-1}
\ end {array}\ right)\) es una lista de números (secuencia finita). El producto interior (Sección 15.4) para nuestros dos espacios son los siguientes:
- Producto interior estándar\(\mathbb{R}^n\):
\ begin {align}
\ langle\ negridsymbol {x},\ negridsymbol {y}\ rangle &=\ negridsymbol {y} ^ {T}\ negridsymbol {x}\ nonumber\\
&=\ sum_ {i=0} ^ {n-1} x_ {i} y_ {i}
\ end {align} - Producto interior estándar\(\mathbb{C}^n\):
\ [\ begin {align}
\ langle\ negridsymbol {x},\ negridsymbol {y}\ rangle &=\ overline {\ boldsymbol {y} ^ {T}}\ negridsymbol {x}\ nonumber\\
&=\ sum_ {i=0} ^ {n-1} x_ {i}\ bar {y} _ {i}
\ end {align}\ nonumber\]
Modelo para: Señales de tiempo discretas en el intervalo\([0,n−1]\) o señales de tiempo discretas periódicas (con período\(n\)). \ [\ left (\ begin {array} {c}
x_ {0}\\
x_ {1}\\
\ puntos\\
x_ {n-1}
\ end {array}\ derecha)\ nonumber\]
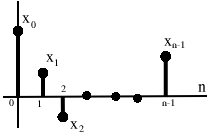
Figura\(\PageIndex{1}\)
\( f \in L^2 ([a,b])\)es una función de energía finita en\([a,b]\)
Producto interno
\[\langle f, g\rangle=\int_{a}^{b} f(t) \overline{g(t)} \mathrm{d} t \nonumber \]
Modelo para: señales de tiempo continuas en el intervalo\([a,b]\) o señales de tiempo continuas periódicas (con período\(T=b−a\))
\(x \in \ell^{2}(\mathbb{Z})\)es una secuencia infinita de números que es sumable al cuadrado
Producto interior
\[\langle x, y\rangle=\sum_{i=-\infty}^{\infty} x[i] \overline{y[i]} \nonumber \]
Modelo para: tiempo discreto, señales no periódicas
\(f \in L^{2}(\mathbb{R})\)es una función de energía finita en todos\(\mathbb{R}\).
Producto interior
\[\langle f, g\rangle=\int_{-\infty}^{\infty} f(t) \overline{g(t)} \mathrm{d} t \nonumber \]
Modelo para: tiempo continuo, señales no periódicas
Análisis de Fourier Asociado
Cada uno de estos 4 espacios de Hilbert tiene asociado un tipo de análisis de Fourier.
- \(L^2([a,b])\)→ Serie de Fourier
- \(\ell^{2}([0, n-1])\)→ Transformada Discreta de Fourier
- \(L^{2}(\mathbb{R})\)→ Transformada de Fourier
- \(\ell^{2}(\mathbb{Z})\)→ Transformada Discreta de Fourier de
Pero los 4 de estos se basan en los mismos principios (el espacio Hilbert).
Nota Importante
No todos los espacios normados son espacios de Hilbert
Por ejemplo:\(L^1(\mathbb{R})\),\(\|f\|_{1}=\int|f(t)| d t\). Inténtalo como puedas, no puedes encontrar un producto interno que induzca esta norma, es decir, un\(\langle\cdot, \cdot\rangle\) tal que
\ [\ begin {align}
\ langle f, f\ rangle &=\ left (\ int (|f (t) |) ^ {2}\ mathrm {d} t\ derecha) ^ {2}\ nonumber\\
&=\ izquierda (\ |f\ |_ {1}\ derecha) ^ {2}
\ end {align}\ nonumber\]
De hecho, de todos los\(L^p(\mathbb{R})\) espacios,\(L^2(\mathbb{R})\) es el único que es un espacio Hilbert.
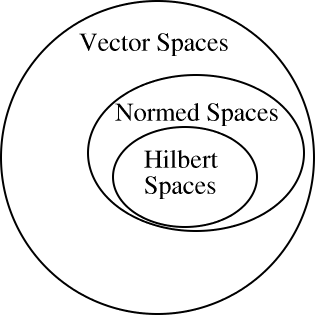
Figura\(\PageIndex{2}\)
Los espacios de Hilbert son, con mucho, los más bonitos. Si usas o estudias la expansión de base ortonormal (Sección 15.9) entonces comenzarás a ver por qué esto es cierto.


