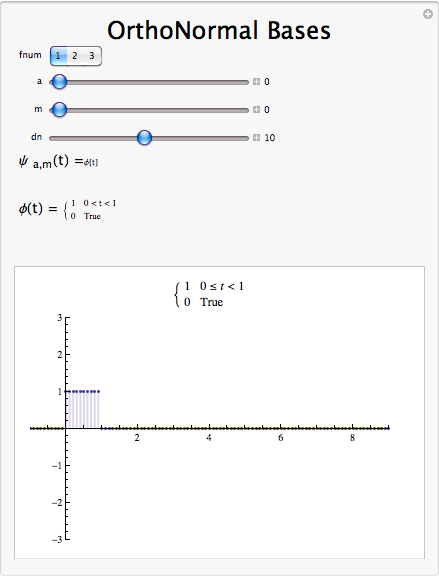
15.11: Base de Ondículas de Haar
- Page ID
- 86563
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introducción
La serie de Fourier es una representación ortonormal útil (Sección 15.9)\(L^2([0,T])\) especialmente para entradas en sistemas LTI. Sin embargo, no es adecuado para algunas aplicaciones, es decir, el procesamiento de imágenes (recordar los fenómenos de Gibb (Sección 6.7)).
Las ondículas, descubiertas en los últimos 15 años, son otro tipo de base para\(L^2([0,T])\) y tienen muchas propiedades agradables.
Comparaciones de Bases
Serie de Fourier -\(c_n\) dar información de frecuencia. Las funciones básicas duran todo el intervalo.
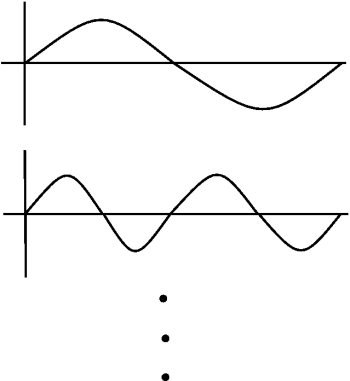
Ondículas: las funciones base dan información de frecuencia pero son locales en el tiempo.
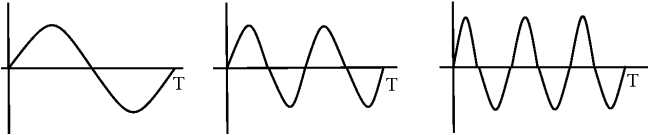
En base a Fourier, las funciones base son múltiplos armónicos de\(e^{j \omega_0 t}\)
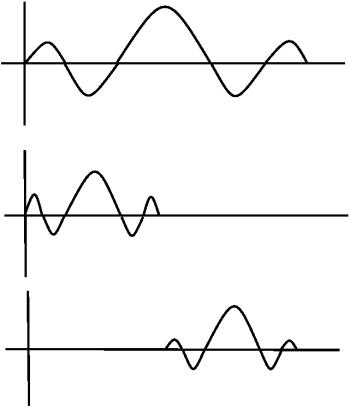
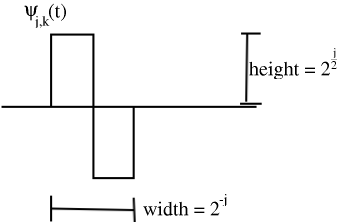
En la base de wavelet Haar, las funciones base se escalan y traducen versiones de una “wavelet madre”\(\psi(t)\).
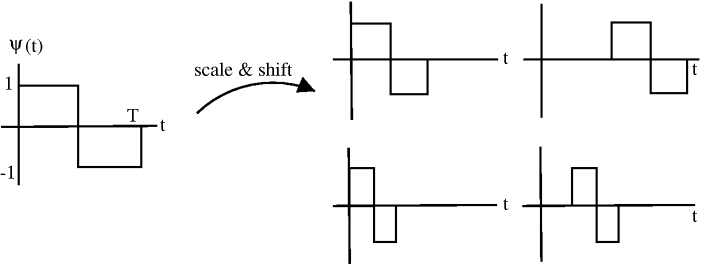
Figura\(\PageIndex{4}\)
Las funciones de base\(\left\{\psi_{j, k}(t)\right\}\) están indexadas por una escala j y un desplazamiento k.
Vamos\(\phi(t)=1\),\(0 \leq t<T\) Entonces\(\left\{\phi(t), 2^{\frac{j}{2}} \psi\left(2^{j} t-k\right), \phi(t), 2^{\frac{j}{2}} \psi\left(2^{j} t-k\right) \mid j \in \mathbb{Z} \text { and }\left(k=0,1,2, \ldots, 2^{j}-1\right)\right\}\).
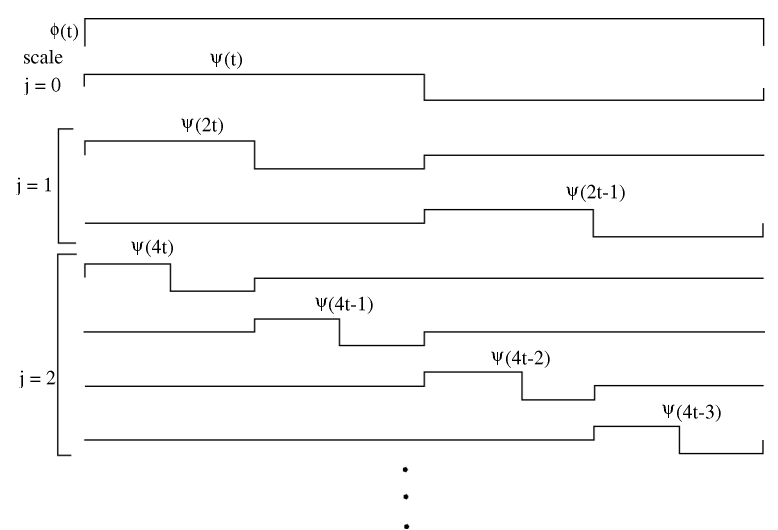
Figura\(\PageIndex{5}\)
\ [\ psi (t) =\ left\ {\ begin {array} {l}
1\ text {if} 0\ leq t<\ frac {T} {2}\\
-1\ text {if} 0\ leq\ frac {T} {2} <T
\ end {array}\ right. \ nonumber\]
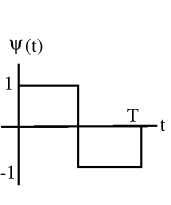
Figura\(\PageIndex{6}\)
Vamos\(\psi_{j, k}(t)=2^{\frac{j}{2}} \psi\left(2^{j} t-k\right)\).
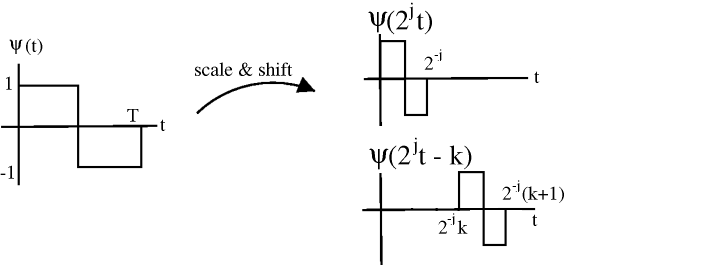
Figura\(\PageIndex{7}\)
Función de base más grande\(j\) → “más flaca”\(j=\{0,1,2, \ldots\}\),\(2^j\) turnos en cada escala:\(k=0,1, \ldots, 2^{j}-1\)
Comprobar: cada uno\(\psi_{j, k}(t)\) tiene unidad de energía
Figura\(\PageIndex{8}\)
\[\left(\int \psi_{j, k}^{2}(t) \mathrm{d} t=1\right) \Rightarrow\left(\left\|\psi_{j, k}(t)\right\|_{2}=1\right) \nonumber \]
Dos funciones básicas cualesquiera son ortogonales.
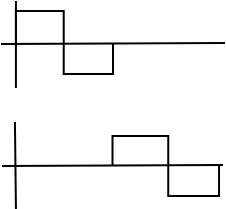
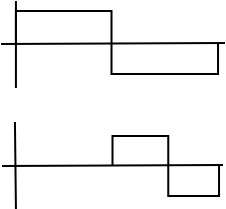
b) Escala diferente
También,\(\left\{\psi_{j, k}, \phi\right\}\) span\(L^2([0,T])\).
Transformación de ondículas Haar
Usando lo que sabemos de los espacios Hilbert (Sección 15.4): Para cualquiera\(f(t) \in L^{2}([0, T])\), podemos escribir
Síntesis
\[f(t)=\sum_{j} \sum_{k} w_{j, k} \psi_{j, k}(t)+c_{0} \phi(t) \nonumber \]
Análisis
\[w_{j, k}=\int_{0}^{T} f(t) \psi_{j, k}(t) d t \nonumber \]
\[c_{0}=\int_{0}^{T} f(t) \phi(t) d t \nonumber \]
Nota
los\(w_{j,k}\) son reales
La transformación Haar es súper útil especialmente en la compresión de imágenes
Demostración de Wavelet de Haar