3.1: Polarización

En muchos materiales eléctricamente aislantes, llamados dieléctricos, los electrones están fuertemente unidos al núcleo. No son móviles, pero si se aplica un campo eléctrico, la nube negativa de electrones puede desplazarse ligeramente del núcleo positivo, como se ilustra en la Figura 3-1 a. Entonces se dice que el material tiene una polarización electrónica. La polarizabilidad orientacional como en la Figura 3-1 b ocurre en moléculas polares que no comparten sus electrones simétricamente de manera que se separan las cargas netas positiva y negativa. Un campo eléctrico aplicado entonces ejerce un par sobre la molécula que tiende a alinearla con el campo. Los iones en una molécula también pueden sufrir ligeros desplazamientos relativos que dan lugar a polarizabilidad iónica.

Figura 3-1 Un dipolo eléctrico consta de dos cargas de igual magnitud pero signo opuesto, separadas por una pequeña distancia vectorial d. (a) La polarización electrónica surge cuando el movimiento promedio de la nube de electrones alrededor de su núcleo se desplaza ligeramente. b) La polarización de orientación surge cuando una molécula polar asimétrica tiende a alinearse con un campo eléctrico aplicado. Si el espaciamiento d también cambia, la molécula tiene polarización iónica.

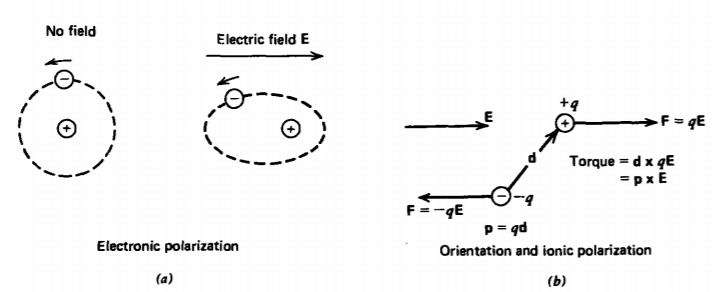
Las cargas ligeramente separadas para estos casos forman dipolos eléctricos. Los materiales dieléctricos tienen una distribución de dichos dipolos. A pesar de que estos materiales son de carga neutra debido a que cada dipolo contiene una cantidad igual de cargas positivas y negativas, una carga neta puede acumularse en una región si hay un desequilibrio local de extremos dipolares positivos o negativos. La carga neta de polarización en dicha región es también una fuente del campo eléctrico además de cualquier otra carga libre.

Dipolo eléctrico

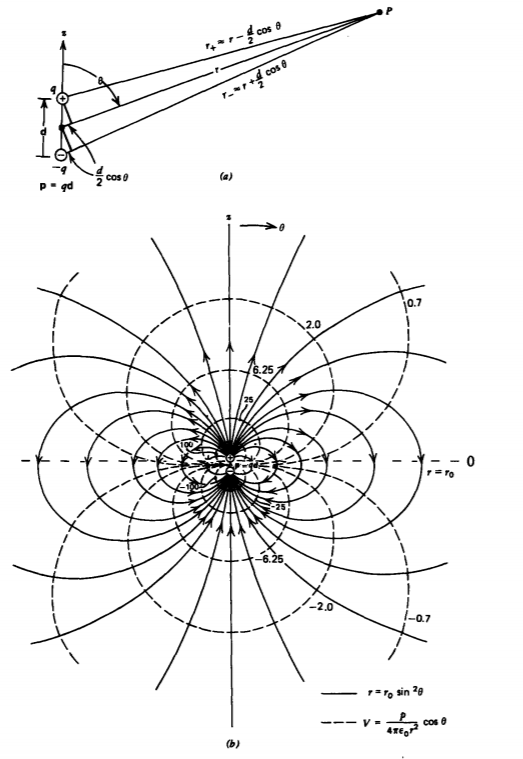
El modelo más simple de un dipolo eléctrico, mostrado en la Figura 3-2a, tiene una carga positiva y negativa de igual magnitud q separadas por un pequeño desplazamiento vectorial d dirigido de la carga negativa a positiva a lo largo del eje z. El potencial eléctrico se encuentra fácilmente en cualquier punto P como la superposición de potenciales de cada carga puntual sola:

\[V = \frac{q}{4 \pi \varepsilon_{0}r_{+}} - \frac{q}{4 \pi \varepsilon_{0}r_{-}} \nonumber \]

El potencial general y la distribución del campo eléctrico para cualquier desplazamiento d se pueden obtener fácilmente a partir de la geometría que relaciona las distancias r ₊ y r _- con las coordenadas esféricas r y\(\theta\). Por simetría, estas distancias son independientes del ángulo\(\phi\). Sin embargo, en los materiales dieléctricos la separación entre cargas son de dimensiones atómicas y por lo tanto son muy pequeñas en comparación con las distancias de interés alejadas del dipolo. Entonces, con r ₊ y r _- mucho mayores que el espaciamiento dipolar d, los aproximamos como

\[\lim_{r>>d} \left. \begin{matrix} r_{+} \approx r - \frac{d}{2} \cos \theta \\ r_{-} \approx r + \frac{d}{2} \cos \theta \end{matrix} \right. \nonumber \]

Entonces el potencial de (1) es aproximadamente

\[V \approx \frac{qd \cos \theta}{4 \pi \varepsilon_{0}r^{2}} = \frac{\textbf{p} \cdot \textbf{i}_{r}}{4 \pi \varepsilon_{0}r^{2}} \nonumber \]

donde el vector p se llama el momento dipolo y se define como

\(\textbf{p}=q \textbf{d}(\textrm{coul-m})\)

Figura 3-2 (a) El potencial en cualquier punto P debido al dipolo eléctrico es igual a la suma de potenciales de cada carga sola. b) Las líneas equipotenciales (discontinuas) y de campo (continuas) para un dipolo eléctrico puntual calibrado para\(4 \pi \varepsilon_{0}/p = 100\).

Debido a que la separación de cargas atómicas es del orden de\(1 \times 10^{-10}\, m\) con una magnitud de carga igual a un múltiplo entero de la carga electrónica (q = 1.6 x 10 ^-19 coul), es conveniente expresar momentos dipolares en unidades de debyes definidos como 1 debye = 3.33 X ^10-30 coul -m para que los momentos dipolares sean del orden p = 1.6 x 10 ^-29 coul-m\(\approx\) 4.8 debyes. El campo eléctrico para el dipolo puntual es entonces

\[\textbf{E} = - \nabla V = \frac{p}{4 \pi \varepsilon_{0}r^{3}} [2 \cos \theta \textbf{i}_{r} + \sin \theta \textbf{i}_{\theta}] = \frac{3(\textbf{p} \cdot \textbf{i}_{r}) \textbf{i}_{r} - \textbf{p}}{4 \pi \varepsilon_{0}r^{3}} \nonumber \]

siendo independientes las últimas expresiones en (3) y (5) coordinadas. El potencial y el campo eléctrico caen como una sola potencia más alta en r sobre la de una carga puntual porque la carga neta del dipolo es cero. A medida que uno se aleja del dipolo, los campos por cada carga tienden a cancelarse. El equipotencial de dipolo puntual y las líneas de campo se esbozan en la Figura 3-2 b. Las líneas tangentes al campo eléctrico son

\[\frac{dr}{r d \theta} = \frac{E_{r}}{E_{\theta}} = 2 \cot \theta \Rightarrow r = r_{0} \sin^{2} \theta \nonumber \]

donde r ₀ es la posición de la línea de campo cuando\(\theta = \pi/2\). Todas las líneas de campo comienzan con la carga positiva y terminan en la carga negativa.

Si hay más de un par de cargas, la definición de momento dipolo en (4) se generaliza a una suma sobre todos los cargos,

\[\textbf{p} = \sum_{\textrm{all charges}} q_{i}\textbf{r}_{i} \nonumber \]

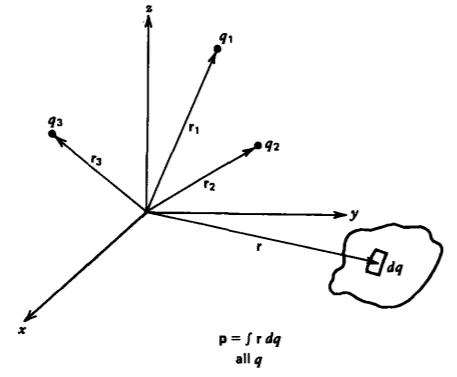
donde r _i es la distancia del vector desde un origen hasta la carga q _i como en la Figura 3-3. Cuando la carga neta en el sistema es cero (\(\sum q_{i} = 0\)), el momento dipolar es independiente de la elección de orígenes para si reemplazamos r _i en (7) por r _i + r ₀, donde r ₀ es la distancia vectorial constante entre dos orígenes:

\[\textbf{p} = \sum q_{i} (\textbf{r}_{i} + \textbf{r}_{0}) \\ = \sum q_{i} \textbf{r}_{i} \textbf{r}_{0} \sum q_{i} \nearrow^{0} \\ = \sum q_{i} \textbf{r}_{i} \nonumber \]

El resultado no cambia desde (7) ya que la constante r _o podría tomarse fuera de la suma.

Si tenemos una distribución continua de carga (7) se generaliza aún más a

\[\textbf{p} = \int_{\textrm{all } q} \textbf{r} dq \nonumber \]

Figura 3-3 El momento dipolar se puede definir para cualquier distribución de carga. Si la carga neta en el sistema es cero, el momento dipolo es independiente de la ubicación del origen.

Entonces el campo potencial y eléctrico lejos de cualquier distribución dipolo viene dado por las expresiones independientes de coordenadas en (3) y (5) donde el momento dipolar p viene dado por (7) y (9).

Carga de polarización

Encerramos un gran número de dipolos dentro de un medio dieléctrico con el volumen rectangular de tamaño diferencial\(\Delta x \: \Delta y \: \Delta z\) mostrado en la Figura 3-4 a. Todos los dipolos totalmente cerrados, al ser de carga neutra, no aportan carga neta dentro del volumen. Solo aquellos dipolos a una distancia\(\textbf{d} \cdot \textbf{n}\) de cada superficie son cortados por el volumen y así aportan una carga neta donde n es la unidad normal a la superficie en cada cara, como en la Figura 3-4 b. Si el número de dipolos por unidad de volumen es N, es conveniente definir la densidad numérica de dipolos como el vector de polarización P:

\[\textbf{P} = N \textbf{p} = Nq \textbf{d} \nonumber \]

La carga neta encerrada cerca de la superficie 1 es

\[dq_{1} = (Nqd_{x})_{\vert x} \Delta y \: \Delta z = P_{x}(x) \Delta y \: \Delta z \nonumber \]

mientras que cerca de la superficie opuesta 2

\[dq_{2} = - (Nqd_{x})_{\vert x + \Delta x} \Delta y \: \Delta z = - P_{x}(x + \Delta x) \: \Delta y \: \Delta z \nonumber \]

Figura 3-4 (a) La carga neta encerrada dentro de un volumen de dipolos de tamaño diferencial solo tiene contribuciones de los dipolos que son cortados por las superficies. Todos los dipolos totalmente cerrados no aportan carga neta. (b) Sólo aquellos dipolos situados a una distancia\(\textbf{d} \cdot \textbf{n}\) de la superficie son cortados por el volumen.

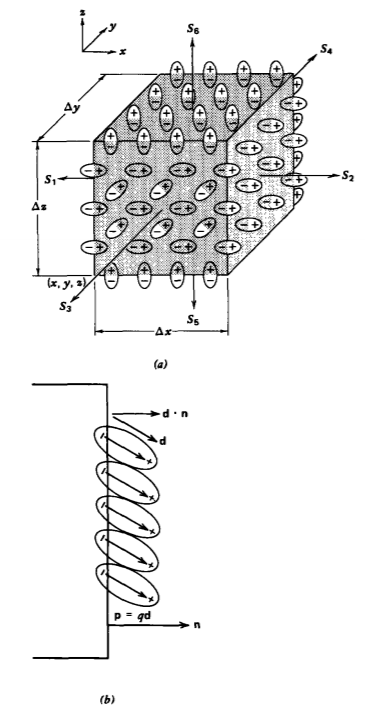
donde asumimos eso\(\Delta y\) y\(\Delta z\) son lo suficientemente pequeños como para que la polarización P sea esencialmente constante sobre la superficie. La polarización puede diferir en la superficie 1 en la coordenada x de la superficie 2 en la coordenada\(x + \Delta x\) si la densidad numérica N, la carga. q, o el desplazamiento d es una función de x. La diferencia en signo entre (11) y (12) se debe a que cerca de _S1 la carga positiva está dentro del volumen, mientras que cerca de S ₂ la carga negativa permanece en el volumen. Obsérvese también que solo el componente de d normal a la superficie contribuye al volumen de carga neta.

Del mismo modo, cerca de las superficies S ₃ y S ₄ la carga neta encerrada es

\[dq_{3} = (Nqd_{y})_{\vert y} \Delta x \: \Delta z = P_{y}(y) \Delta x \: \Delta z \\ dq_{4} = -(Nqd_{y})_{\vert y + \Delta y} \Delta x \: \Delta z = -P_{y}(y + \Delta y) \Delta x \: \Delta z \nonumber \]

mientras que cerca de las superficies S ₅ y S ₆ con normal en la dirección z la carga neta encerrada es

\[dq_{5} = (Nqd_{z})_{\vert z} \Delta x \: \Delta y \: = P_{z}(z)\Delta x \: \Delta y \\ dq_{6} = -(Nqd_{z})_{\vert + \Delta z} \Delta x \: \Delta y = -P_{z}(z + \Delta z) \Delta x \: \Delta y \nonumber \]

El cargo total encerrado dentro del volumen es la suma de (11) - (14):

\[dq_{T} = dq_{1} + dq_{2} + dq_{3} + dq_{4} + dq_{5} + dq_{6} \\ = (\frac{P_{x}(x) - P_{x}(x + \Delta x)}{\Delta x} + \frac{P_{y}(y) - P_{y}(y + \Delta y)}{\Delta y} \\ + \frac{P_{z}(z) - P_{z}(z + \Delta z)}{\Delta z}) \Delta x \: \Delta y \: \Delta z \nonumber \]

A medida que el volumen se contrae a tamaño cero, los términos de polarización en (15) definen derivadas parciales de modo que la densidad de carga del volumen de polarización es

\[\rho_{p} = \lim_{\Delta x \rightarrow 0 \\ \Delta y \rightarrow 0 \\ \Delta z \rightarrow 0} \frac{dq_{T}}{\Delta x \: \Delta y \: \Delta z} = -(\frac{\partial P_{x}}{\partial x} + \frac{\partial P_{y}}{\partial y} + \frac{\partial P_{z}}{\partial z}) = - \nabla \cdot \textbf{P} \nonumber \]

Esta carga por volumen también es una fuente del campo eléctrico y necesita ser incluida en la ley de Gauss

\[\nabla \cdot (\varepsilon_{0}\textbf{E}) = \rho_{f} + \rho_{p} = \rho_{f} - \nabla \cdot \textbf{P} \nonumber \]

donde subindicamos el cargo gratuito\(\rho_{f}\) con la letra\(f\) para distinguirlo de la carga de polarización\(\rho_{p}\). La carga de polarización total dentro de una región se obtiene integrando (16) sobre el volumen,

\[q_{p} = \int_{V} \rho_{p}dV = - \int_{V} \nabla \cdot \textbf{P} dV = - \oint_{S} \textbf{P} \cdot \textbf{dS} \nonumber \]

donde se utilizó el teorema de divergencia para relacionar la carga de polarización con una integral superficial del vector de polarización.

Campo de Desplazamiento

Como no tenemos una forma directa de controlar la carga de polarización, es conveniente emitir la ley de Gauss solo en términos de libre carga definiendo un nuevo vector D como

\[\textbf{D} = \varepsilon_{0} \textbf{E} + \textbf{P} \nonumber \]

Este vector D se llama campo de desplazamiento porque difiere de\(\varepsilon_{0} \textbf{E}\) debido a los ligeros desplazamientos de carga en dipolos eléctricos. Usando (19), (17) se puede reescribir como

\[\nabla \cdot (\varepsilon \textbf{E} + \textbf{P}) = \nabla \cdot \textbf{D} = \rho_{f} \nonumber \]

donde pf solo incluye la carga gratuita y no la carga de polarización ligada. Al integrar ambos lados de (20) sobre un volumen y usar el teorema de la divergencia, la nueva forma integral de la ley de Gauss es

\[\int_{V} \nabla \cdot \textbf{D} dV = \oint_{S} \textbf{D} \cdot \textbf{dS} = \int_{V} \rho_{F}dV \nonumber \]

En el espacio libre, la polarización P es cero para que\(\textbf{D} = \varepsilon_{0}\textbf{E}\) y (20) - (21) reduzcan a las leyes del espacio libre utilizadas en el Capítulo 2.

Dieléctricos Lineales

Ahora es necesario encontrar la ley constitutiva que relaciona la polarización P con el campo eléctrico aplicado E. Una discusión precisa requeriría el uso de la mecánica cuántica, lo que está más allá del alcance de este texto. Sin embargo, un modelo clásico simplificado puede ser utilizado para ayudarnos a comprender cualitativamente el caso más interesante de un dieléctrico lineal.

a) Polarizabilidad

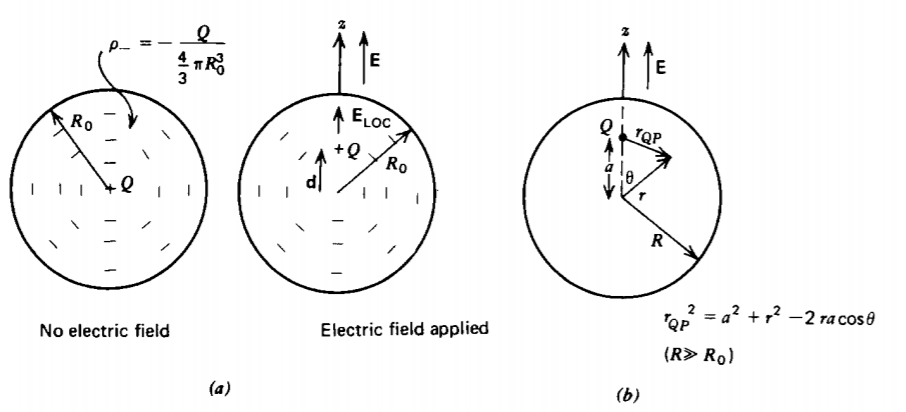
Modelamos el átomo como un núcleo positivo fijo con una nube de electrones negativos esférica uniforme circundante, como se muestra en la Figura 3-5 a. En ausencia de un campo eléctrico aplicado, el momento dipolar es cero porque el centro de carga para la nube de electrones es coincidente con el núcleo. De manera más formal, podemos mostrar esto usando (9), recogiendo nuestro origen en la posición del núcleo:

\[\textbf{p} = Q(0) \nearrow^{0} - \int_{\phi = 0}^{2 \pi} \int_{\theta = 0}^{\pi} \int_{r=0}^{R_{0}} \textbf{i}_{r}\rho_{0}r^{3} \sin \theta dr \: \d \theta \: d \phi \nonumber \]

Dado que el vector unitario radial i _r cambia de dirección en el espacio, es necesario usar la Tabla 1-2 para escribir i _r en términos de los vectores unitarios cartesianos constantes:

\[\textbf{i}_{r} = \sin \theta \cos \phi \textbf{i}_{x} + \sin \theta \sin \phi \textbf{i}_{y} = \cos \theta \textbf{i}_{z} \nonumber \]

Figura 3-5 (a) Un modelo clásico atómico simple tiene una nube de electrones esféricos negativos de pequeño radio _R0 centrada alrededor de un núcleo positivo cuando no hay campo eléctrico externo presente. Un campo eléctrico aplicado tiende a mover la carga positiva en la dirección del campo y la carga negativa en la dirección opuesta creando un dipolo eléctrico. (b) El campo eléctrico promedio dentro de una gran esfera de radio R (R >> R ₀) que encierra muchos dipolos puntuales se encuentra superponiendo los campos promedio debido a cada carga puntual

Cuando se usa (23) en (22) los componentes x e y se integran a cero cuando se integran sobre\(\phi\), mientras que el componente z es cero cuando se integra sobre de\(\theta\) manera que p = 0.

Un campo eléctrico aplicado tiende a empujar la carga positiva en la dirección del campo y la carga negativa en la dirección opuesta provocando un ligero desplazamiento d entre el centro de la nube esférica y el núcleo positivo, como en la Figura 3-5 a. Oponerse a este movimiento se encuentra la atractiva fuerza coulómbica. Considerando el centro de la nube esférica como nuestro origen, el campo autoeléctrico dentro de la nube se encuentra en la Sección 2.4.3 b como

\[E_{r} = - \frac{Qr}{4 \pi \varepsilon_{0}R_{0}^{3}} \nonumber \]

En equilibrio la fuerza neta F sobre la carga positiva es cero,

\[\textbf{F} = Q(\textbf{E}_{\textrm{Loc}} - \frac{Q\textbf{d}}{4 \pi \varepsilon_{0}R_{0}^{3}}) = 0 \nonumber \]

donde evaluamos (24) a r = d y E _Loc es el campo eléctrico polarizador local que actúa sobre el dipolo. De (25) el espaciamiento dipolo de equilibrio es

\[\textbf{d} = \frac{4 \pi \varepsilon_{0}R_{0}^{3}}{Q}\textbf{E}_{\textrm{Loc}} \nonumber \]

para que el momento dipolo se escriba como

\[\textbf{p} = Q \textbf{d} = \alpha \textbf{E}_{\textrm{Loc}}, \: \: \: \alpha = 4 \pi \varepsilon_{0}R_{0}^{3} \nonumber \]

donde\(\alpha\) se llama la polarizabilidad.

b) El Campo Eléctrico Local

Si este dipolo fuera aislado, el campo eléctrico local sería igual al campo macroscópico aplicado. Sin embargo, una gran densidad numérica N de dipolos vecinos también contribuye al campo eléctrico polarizador. El campo eléctrico cambia drásticamente de punto a punto dentro de un pequeño volumen que contiene muchos dipolos, siendo igual a la superposición de campos debido a cada dipolo dado por (5). El campo macroscópico es entonces el campo promedio sobre este pequeño volumen

Calculamos este campo promedio encontrando primero el campo promedio debido a una carga puntual única Q una distancia a a lo largo del eje z desde el centro de un volumen esférico con radio R mucho mayor que el radio de la nube de electrones (R >> R ₀) como en la Figura 3-5b. El campo promedio debido a esta carga sobre el volumen esférico es

\[<\textbf{E}> = \frac{1}{\frac{4}{3} \pi R^{3}} \int_{r=0}^{R} \int_{\theta = 0}^{\pi} \int_{\phi=0}^{2 \pi} \frac{Q(r \textbf{i}_{r} - a \textbf{i}_{z})r^{2} \sin \theta dr \: d \theta \: d \phi}{4 \pi \varepsilon_{0}[a^{2} + r^{2} - 2 r a \: \cos \theta]^{3/2}} \nonumber \]

donde usamos las relaciones

\[r^{2}_{QP} = a^{2} + r^{2} - 2ra \cos \theta, \: \: \: \: \textbf{r}_{QP} = r \textbf{i}_{r} - a \textbf{i}_{z} \nonumber \]

El uso de (23) en (28) de nuevo da como resultado que los componentes x e y sean cero cuando se integran sobre\(\phi\). Solo el componente z es ahora distinto de cero:

\[<E_{z}> = \frac{Q}{\frac{4}{3} \pi R^{3}} \frac{2 \pi}{(4 \pi \varepsilon_{0})} \int_{\theta = 0}^{\pi} \int_{r=0}^{R} \frac{r^{3}(\cos \theta - a/r) \sin \: \theta \: dr \: d \theta}{[a^{2} + r^{2} - 2ra \: \cos \: \theta]^{3/2}} \nonumber \]

Introducimos el cambio de variable de\(\theta\) a u

\[u = r^{2} + a^{2} - 2ar \cos \theta, \: \: \: \: du = 2 ar \: \sin \theta \: d \theta \nonumber \]

para que (30) se pueda integrar sobre u y r. Realizando la integración u primero tenemos

\[<E_{z}> = \frac{3Q}{8 \pi R^{3} \varepsilon_{0}} \int_{r=0}^{R} \int_{(r-a)^{2}}^{(r+a)^{2}} \frac{r}{4 a^{2}} \frac{(r^{2}-a^{2}-u)}{u^{3/2}} dr du \\ = \frac{3Q}{8 \pi R^{3} \varepsilon_{0}} \int_{r=0}^{R} \frac{r}{4a^{2}} (-\frac{2(r^{2} -a^{2} + u)}{u^{1/2}}) \bigg|_{u = (r-a)^{2}}^{(r+a)^{2}} dr \\ = - \frac{3Q}{8 \pi R^{3} \varepsilon_{0}a^{2}} \int_{r=0}^{R} r^{2}(1-\frac{r-a}{\vert r - a \vert})dr \nonumber \]

Tuvimos cuidado de asegurarnos de tomar la raíz cuadrada positiva en el límite inferior de u. Entonces para r > a, la integral es cero de manera que los límites integrales sobre r van de 0 a a:

\[<E_{z}> = - \frac{3Q}{8 \pi R^{3} \varepsilon_{0}a^{2}} \int_{r=0}^{a} 2r^{2} dr = \frac{-Qa}{4 \pi \varepsilon_{0}R^{3}} \nonumber \]

Para formar un dipolo agregamos una carga negativa - Q, una pequeña distancia d por debajo de la carga original. El campo eléctrico promedio debido al dipolo es entonces la superposición de (33) para ambas cargas:

\[<E_{z}> = - \frac{Q}{4 \pi \varepsilon_{0}R^{3}}[a-(a-d)] = - \frac{Qd}{4 \pi \varepsilon_{0}R^{3}} = - \frac{p}{4 \pi \varepsilon_{0}R^{3}} \nonumber \]

Si tenemos una densidad numérica N de tales dipolos dentro de la esfera, el número total de dipolos encerrados es tal\(\frac{4}{3} \pi R^{3}N\) que la superposición de (34) nos da el campo eléctrico promedio debido a todos los dipolos en términos del vector de polarización P = N p:

\[<\textbf{E}> = - \frac{\frac{4}{3} \pi R^{3} N \textbf{p}}{4 \pi \varepsilon_{0} R^{3}} = - \frac{\textbf{P}}{3 \varepsilon_{0}} \nonumber \]

El campo macroscópico total es entonces la suma del campo local visto por cada dipolo y el campo promedio resultante debido a todos los dipolos

\[\textbf{E} = <\textbf{E}> + \textbf{E}_{\textrm{Loc}} = - \frac{\textbf{P}{3 \varepsilon_{0}} + \textbf{E}_{\textrm{Loc}} \nonumber \]

de manera que la polarización P se relaciona con el campo eléctrico macroscópico de (27) como

\[\textbf{P} = N \textbf{p} = N \alpha \textbf{E}_{\textrm{Loc}} = N \alpha (\textbf{E} + \frac{\textbf{P}}{3 \varepsilon_{0}}) \nonumber \]

que se puede resolver para P como

\[\textbf{P} = \frac{N \alpha}{1 - N \alpha/3 \varepsilon_{0}} \textbf{E} = \chi_{e} \varepsilon_{0} \textbf{E}, \: \: \: \chi_{e} = \frac{N \alpha /\varepsilon_{0}}{1 - N \alpha / 3 \varepsilon_{0}} \nonumber \]

donde introducimos la susceptibilidad eléctrica\(\chi_{e}\) como la constante de proporcionalidad entre P y\(\varepsilon_{0}\textbf{E}\). Entonces, el uso de (38) en (19) relaciona el campo de desplazamiento D linealmente con el campo eléctrico:

\[\textbf{D} = \varepsilon_{0} \textbf{E} + \textbf{P} = \varepsilon_{0}(1 + \chi_{e}) \textbf{E} = \varepsilon_{0} \varepsilon_{r} \text f{E} = \varepsilon \textbf{E} \nonumber \]

donde\(\varepsilon_{r} = 1 + \chi_{e}\) se llama la constante dieléctrica relativa y\(\varepsilon = \varepsilon_{r} \varepsilon_{0}\) es la permitividad del dieléctrico, también llamada simplemente la constante dieléctrica. En el espacio libre la susceptibilidad es cero (\(\chi_{e} = 0\)) por lo que\(\varepsilon_{r} = 1\) y la permitividad es la del espacio libre,\(\varepsilon = \varepsilon_{0}\). La última relación en (39) suele ser la más conveniente de usar ya que todos los resultados del Capítulo 2 también son correctos dentro

dieléctricos lineales si reemplazamos\(\varepsilon_{0}\) por\(\varepsilon\). Los valores típicos de permitividad relativa se enumeran en el Cuadro 3-1 para diversas sustancias comunes. Los materiales de alta constante dieléctrica suelen estar compuestos por moléculas altamente polares.

Tabla 3-1 La permitividad relativa para diversas sustancias comunes a temperatura ambiente

	\(\varepsilon = \varepsilon / \varepsilon_{0}\)
Tetracloruro de Carbono ^a	\ (\ varepsilon =\ varepsilon/\ varepsilon_ {0}\) ">2.2
Etanol ^a	\ (\ varepsilon =\ varepsilon/\ varepsilon_ {0}\) ">24
Metanol ^a	\ (\ varepsilon =\ varepsilon/\ varepsilon_ {0}\) ">33
n -Hexano ^a	\ (\ varepsilon =\ varepsilon/\ varepsilon_ {0}\) ">1.9
Nitrobenceno ^a	\ (\ varepsilon =\ varepsilon/\ varepsilon_ {0}\) ">35
Agua Pura ^a	\ (\ varepsilon =\ varepsilon/\ varepsilon_ {0}\) ">80
Titanato de Bario ^b (con 20% de Titanato de Estroncio)	\ (\ varepsilon =\ varepsilon/\ varepsilon_ {0}\) ">>2100
Vidrio de Borosilicato ^b	\ (\ varepsilon =\ varepsilon/\ varepsilon_ {0}\) ">4.0
Mica Rubí (Moscovita) ^b	\ (\ varepsilon =\ varepsilon/\ varepsilon_ {0}\) ">5.4
Polietileno ^b	\ (\ varepsilon =\ varepsilon/\ varepsilon_ {0}\) ">2.2
Cloruro de Polivinilo ^b	\ (\ varepsilon =\ varepsilon/\ varepsilon_ {0}\) ">6.1
Teflon ^b Politetrafluoretileno)	\ (\ varepsilon =\ varepsilon/\ varepsilon_ {0}\) ">2.1
Plexiglás ^b	\ (\ varepsilon =\ varepsilon/\ varepsilon_ {0}\) ">3.4
Cera Parafina ^b	\ (\ varepsilon =\ varepsilon/\ varepsilon_ {0}\) ">2.2

^a Del Manual de Química de Lange, 10a ed., McGraw-Hill, Nueva York, 1961, pp. 1234-37.

^b De A. R. von Hippel (Ed.) Materiales dieléctricos y aplicaciones, M.I.T., Cambridge, Mass., 1966, pp. 301-370

La polarizabilidad y el campo eléctrico local solo se introdujeron para que pudiéramos relacionar los campos microscópicos y macroscópicos. Para la mayoría de los problemas futuros describiremos los materiales por su permitividad\(\varepsilon\) porque esta constante se mide más fácilmente. La polarizabilidad se encuentra entonces fácilmente como

\[\varepsilon - \varepsilon_{0} = \frac{N \alpha}{1 - N \alpha/3 \varepsilon_{0}} \Right \frac{N \alpha}{3 \varepsilon_{0}} = \frac{\varepsilon - \varepsilon_{0}}{\varepsilon + 2 \varepsilon_{0}} \nonumber \]

Entonces se vuelve más sencillo trabajar con los vectores de campo D y E. La polarización siempre se puede obtener si es necesario a partir de la definición

\[\textbf{P} = \textbf{D] - \varepsilon_{0} \textbf{E} = (\varepsilon - \varepsilon_{0}0 \textbf{E} \nonumber \]

Ejemplo 3-1: Carga puntual dentro de una esfera dieléctrica

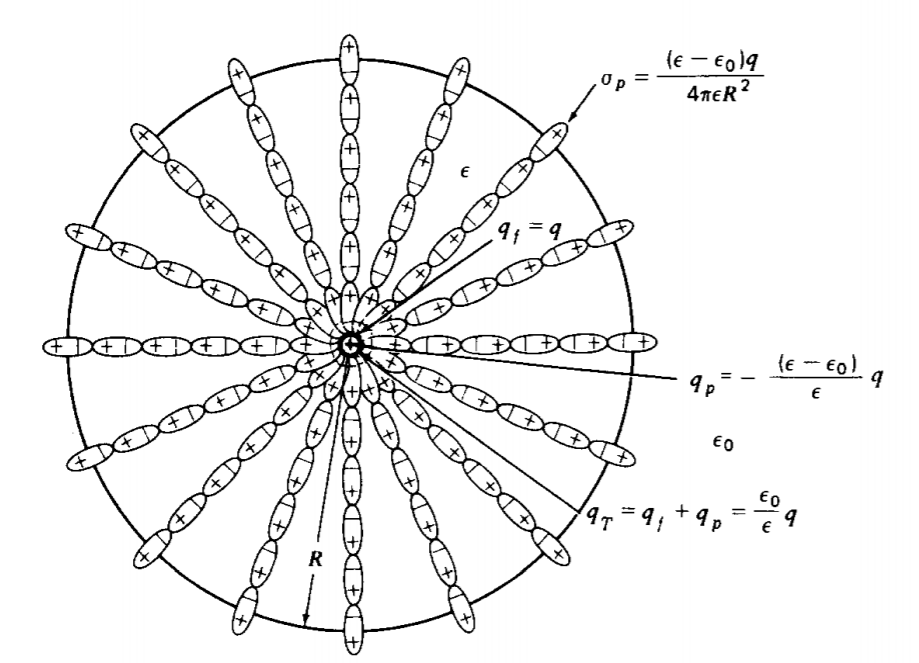
Encuentra todos los campos y cargas debidas a una carga puntual q dentro de una esfera dieléctrica lineal de radio R y permitividad\(\varepsilon\) rodeada de espacio libre, como en la Figura 3-6.

Figura 3-6 El campo eléctrico debido a una carga puntual dentro de una esfera dieléctrica es menor que el campo de espacio libre debido a la neutralización parcial de la carga puntual por la acumulación de extremos dipolares de carga opuesta. La carga de polarización total en la esfera permanece cero como una magnitud igual pero la carga de polarización de signo opuesto aparece en la interfaz esférica.

Contestar

Aplicando la ley de Gauss de (2 1) a una esfera de cualquier radio r ya sea dentro o fuera de la esfera, el cargo libre cerrado es siempre q:

\(\oint_{S} \textbf{D} \cdot \textbf{S} = D_{r}4 \pi r^{2} = q \Rightarrow D_{r} = \frac{q}{4 \pi r^{2}} \textrm{ all } r\)

El campo eléctrico es entonces discontinuo a r = R,

\(E_{r} = \left \{ \begin{matrix} \frac{D_{r}}{\varepsilon} = \frac{q}{4 \pi \varepsilon r^{2} & r<R \\ \frac{D_{r}}{\varepsilon_{0}} = \frac{q}{4 \pi \varepsilon_{0}r^{2} & r>R \end{matrix} \right.\)

debido al cambio abrupto de permitividades. El campo de polarización es

\(P_{r} = D_{r} - \varepsilon_{0} E_{r} = \left \{ \begin{matrix} \frac{(\varepsilon - \varepsilon_{0})q}{4 \pi \varepsilon r^{2}}, & r < R \\ 0, & r>R \end{matrix} \right.\)

La carga de polarización de volumen\(\rho_{P}\) es cero en todas partes

\(\rho_{p} = - \nabla \cdot \textbf{P} = - \frac{1}{r^{2}} \frac{\partial}{\partial r} (r^{2} P_{r}) = 0, \: \: \: 0 < r < R\)

excepto en r = 0 donde está presente una carga de polarización puntual, y en r = R donde tenemos una carga de polarización superficial encontrada usando (18) para esferas gaussianas concéntricas de radio r dentro y fuera de la esfera dieléctrica:

\(q_{p} = - \oint_{S} \textbf{P} \cdot \textbf{dS}= - P_{r}4 \pi r^{2} = \left \{ \begin{matrix} - (\varepsilon - \varepsilon_{0})q/\varepsilon, & r<R \\ 0 & r>R \end{matrix} \right. \)

Sabemos que para r < R esta carga de polarización debe ser una carga puntual en el origen ya que no hay contribución de carga volumétrica que arroje una carga puntual total en el origen:

\(Q_{T} = q_{p} + q = \frac{\varepsilon_{0}}{\varepsilon} q\)

Esta reducción de la carga neta es por lo que el campo eléctrico dentro de la esfera es menor que el valor del espacio libre. Los extremos de polaridad opuesta de los dipolos son atraídos hacia la carga puntual, neutralizándola parcialmente. La carga de polarización total encerrada por la esfera con r > R es cero ya que hay una carga de polarización superficial de polaridad opuesta a r = R con densidad,

\(\sigma_{p} = \frac{(\varepsilon - \varepsilon_{0})q}{4 \pi \varepsilon R^{2}}\)

La carga superficial total\(\sigma_{p} 4 \pi R^{2} = (\varepsilon - \varepsilon_{0}) q/\varepsilon\) es igual en magnitud pero opuesta en signo a la carga del punto de polarización en el origen. El cargo total de p6larización siempre suma a cero.

Polarización espontánea

(a) Ferro-eléctricos Examinando (38) vemos que cuando\(N \alpha/3 \varepsilon_{0}=1\) la polarización puede ser distinta de cero aunque el campo eléctrico sea cero. Podemos simplemente cumplir con esta condición usando el valor de polarizabilidad en (27) para polarización electrónica si todo el volumen está lleno de esferas dipolares de contacto del tipo de la Figura 3-5a para que tengamos un dipolo por cada volumen de\(\frac{4}{3} \pi R_{0}^{3}\) Entonces cualquier ligera fluctuación en el campo eléctrico local aumenta la polarización, lo que a su vez aumenta el campo local dando como resultado una polarización espontánea para que todos los dipolos de una región estén alineados. En un material real los dipolos no están tan densamente empaquetados. Además, modelos estadísticos más realistas, incluyendo movimientos inducidos térmicamente, han demostrado que la mayoría de las moléculas no pueden cumplir con las condiciones para la polarización espontánea.

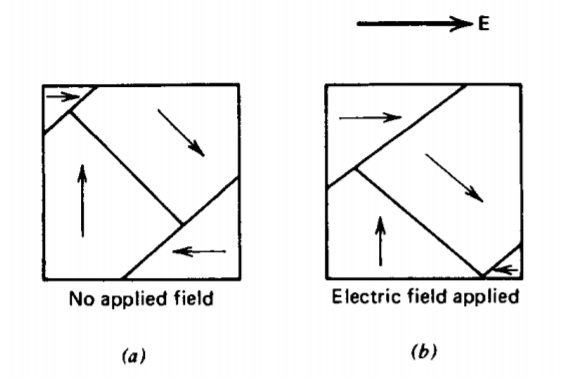
Sin embargo, algunos materiales tienen suficientes contribuciones adicionales a las polarizabilidades debido a la polarización iónica y orientacional que se cumple la condición de polarización espontánea. Dichos materiales se denominan ferroeléctricos, aunque no sean compuestos de hierro, por su similitud en el comportamiento con los materiales ferromagnéticos compuestos de hierro, lo que discutimos en la Sección 5.5.3 c. Los ferroeléctricos están compuestos por regiones permanentemente polarizadas, llamadas dominios, como se ilustra en la Figura 3-7 a. En ausencia de un campo eléctrico, estos dominios se distribuyen aleatoriamente de manera que el campo de polarización macroscópica neta sea cero. Cuando se aplica un campo eléctrico, los dipolos tienden a alinearse con el campo de manera que los dominios con un componente de polarización a lo largo del campo crecen a expensas de los dominios no alineados. Los ferroeléctricos suelen tener permitividades muy altas, como el titanato de bario enumerado en la Tabla 3-1.

Los dominios no responden directamente con el campo eléctrico ya que la orientación del dominio y el crecimiento no es un proceso reversible sino que implica pérdidas. La polarización P se relaciona entonces de manera no lineal con el campo eléctrico E mediante la curva de histéresis mostrada en la Figura 3-8. La polarización de una muestra inicialmente no polarizada aumenta con el campo eléctrico de manera no lineal hasta que se alcanza el valor de saturación P _sat cuando todos los dominios están completamente alineados con el campo. Un incremento adicional en E no aumenta P ya que todos los dipolos están completamente alineados.

A medida que el campo disminuye, la polarización no retrocede su trayectoria sino que sigue un nuevo camino ya que los dipolos tienden a adherirse a sus posiciones anteriores. Incluso cuando el campo eléctrico es cero, un

Figura 3-7 (a) En ausencia de un campo eléctrico aplicado, un material ferroeléctrico generalmente tiene dominios polarizados permanentemente distribuidos aleatoriamente. Sobre un volumen macroscópico, la polarización neta debida a todos los dominios es cero. (b) Cuando se aplica un campo eléctrico, los dominios con un componente de polarización en la dirección del campo crecen a expensas de dominios no alineados para que pueda resultar una polarización neta.

Figura 3-8 Una curva típica de histéresis ferroeléctrica muestra un valor de saturación P _sat cuando todos los dominios se alinean con el campo, una polarización remanente P _r cuando se elimina el campo eléctrico, y un campo eléctrico coercitivo negativo - E _c, necesario para llevar la polarización volver a cero.

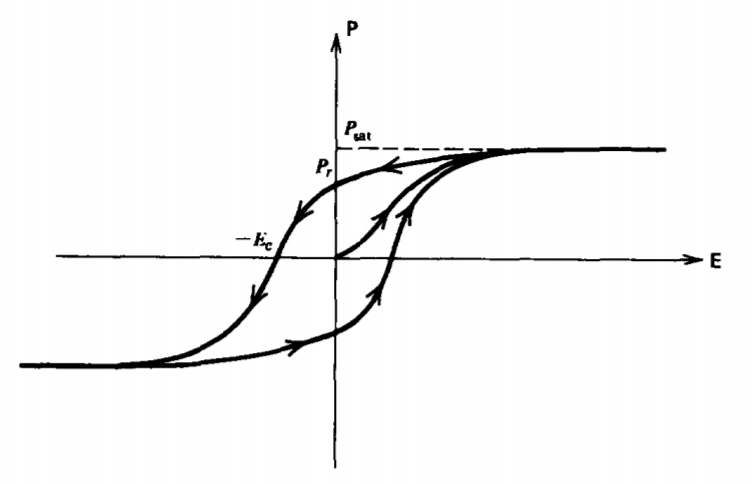
polarización remanente P _r permanece. Para llevar la polarización a cero se requiere un campo coercitivo negativo - E _c. Otros aumentos de magnitud en el campo eléctrico negativo continúan el bucle de histéresis simétrica hasta que se alcanza una saturación negativa donde todos los dipolos se han volteado. Si el campo se lleva ahora a cero y continúa a valores de campo positivos, se recorre toda la curva de histéresis.

b) Electretes

Hay una clase de materiales llamados electretes que también exhiben una polarización permanente incluso en ausencia de un campo eléctrico aplicado. Los electretes se hacen típicamente usando ciertas ceras o plásticos que se calientan hasta que se vuelven blandos. Se colocan dentro de un campo eléctrico, tendiendo a alinear los dipolos en la misma dirección que el campo eléctrico, y luego se dejan endurecer. Los dipolos se congelan entonces en su lugar de manera que incluso cuando se elimina el campo eléctrico queda una polarización permanente.

Otros fenómenos de polarización interesantes son:

Electrostricción - ligero cambio de tamaño de un dieléctrico debido a la fuerza eléctrica sobre los dipolos.

Piezo-electricidad - cuando el efecto electroestrictivo es reversible de manera que una tensión mecánica también crea un campo.

Polarización inducida por piroelectricidad por calentamiento o enfriamiento.