3.2: Conducción

Conservación de Carga

A diferencia de los dieléctricos, la mayoría de los metales tienen su banda externa de electrones solo débilmente ligada al núcleo y son libres de moverse en un campo eléctrico aplicado. En las soluciones electrolíticas, los iones de ambos signos son libres de moverse. El flujo de carga, llamado corriente, se define como la carga total que fluye a través de una superficie por unidad de tiempo. En la Figura 3-9a una sola especie de carga libre con densidad\(\rho_{fi}\) y velocidad\(\textbf{v}_{i}\) fluye a través de una superficie dS de tamaño diferencial pequeño.

Figura 3-9 La corriente a través de una superficie se define como el número de cargas por segundo que pasan a través de la superficie. (a) La corriente es proporcional al componente de velocidad de carga perpendicular a la superficie. b) El cambio neto de la carga total dentro de un volumen es igual a la diferencia de la carga que ingresa a la que sale en poco tiempo\(\Delta t\).

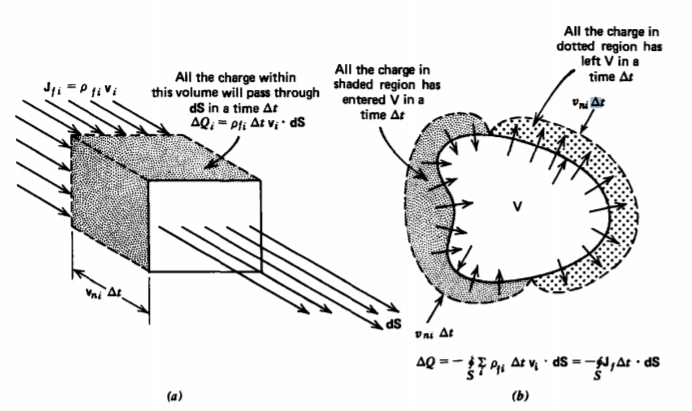
La carga total que fluye a través de esta superficie en un tiempo\(\Delta t\) depende solo de la componente de velocidad perpendicular a la superficie:

\[\Delta Q_{i} = \rho_{fi} \Delta t \textbf{v}_{i} \cdot \textbf{dS} \nonumber \]

El componente tangencial de la velocidad paralela a la superficie dS solo da como resultado un flujo de carga a lo largo de la superficie pero no a través de ella. La corriente diferencial total a través de dS se define entonces como

\[dI_{i} = \frac{\Delta Q_{i}}{\Delta t} = \rho_{fi}\textbf{v}_{i} \cdot \textbf{dS} = \textbf{J}_{fi} \cdot \textbf{dS} \: \textrm{ ampere} \nonumber \]

donde la densidad de corriente libre de estas cargas\(\textbf{J}_{fi}\) es un vector y se define como

\[\textbf{J}_{fi} = \rho_{fi} \textbf{v}_{i} \textrm{amp/m}^{2} \nonumber \]

Si hay más de un tipo de portador de carga, la densidad de carga neta es igual a la suma algebraica de todas las densidades de carga, mientras que la densidad de corriente neta es igual a la suma vectorial de las densidades de corriente debidas a cada portadora:

\[\rho_{f} = \sum \rho_{fi}, \: \: \textbf{J}_{f} = \sum \rho_{fi}\textbf{v}_{i} \nonumber \]

Así, aunque tengamos neutralidad de carga para que\(\rho_{f} = 0\), una corriente neta pueda fluir si las cargas se mueven con diferentes velocidades. Por ejemplo, dos portadores de carga opuesta con densidades que\(\rho_{1} = - \rho_{2} \equiv \rho_{0}\) se mueven con velocidades respectivas\(\textbf{v}_{1}\) y\(\textbf{v}_{2}\) tienen

\[\rho_{f} = \rho_{1} + \rho_{2} = 0, \: \: \: \textbf{J}_{f} = \rho_{1} \textbf{v}_{1} + \rho_{2} \textbf{v}_{2} = \rho_{0} (\textbf{v}_{1} - \textbf{v}_{2}) \nonumber \]

Con\(\textbf{v}_{1} \neq \textbf{v}_{2}\) una corriente neta fluye con carga neta cero. Esto es típico en metales donde los electrones son libres de fluir mientras que los núcleos con carga opuesta permanecen estacionarios.

La corriente total I, un escalar, que fluye a través de una superficie macroscópica S, es entonces solo la suma de las corrientes diferenciales totales de todos los portadores de carga a través de cada elemento de superficie de tamaño incremental:

\[I = \int_{S} \textbf{J}_{f} \cdot \textbf{dS} \nonumber \]

Ahora considere el flujo de carga a través del volumen cerrado V con superficie S que se muestra en la Figura 3-9 b. Un tiempo Más tarde, esa carga dentro del volumen cerca de la superficie con el componente de velocidad hacia afuera dejará el volumen, mientras que esa carga justo fuera del volumen con un componente de velocidad hacia adentro apenas entrará en el volumen. La diferencia en la carga total es transportada por la corriente:

\[\Delta Q = \int_{V} [\rho_{f}(t + \Delta t) \rho_{f}(t)] \textrm{dV} \\ = - \oint_{S} \sum \rho_{fi} \textbf{v}_{i} \Delta t \cdot \textbf{dS} = - \oint_{S} \textbf{J}_{f} \Delta t \cdot \textbf{dS} \nonumber \]

El signo menos a la derecha es necesario porque cuando v _i está en la dirección de dS, la carga ha dejado el volumen para que la carga encerrada disminuya. Dividiendo (7) por\(\Delta t\) y tomando el límite como\(\Delta t \rightarrow 0\), usamos (3) para derivar la ecuación de conservación integral de carga:

\[\oint_{S} \textbf{J}_{f} \cdot \textbf{dS} + \int_{\textrm{V}} \frac{\partial \rho_{f}}{\partial t} d \textrm{V} = 0 \nonumber \]

Usando el teorema de divergencia, la integral de superficie se puede convertir en una integral de volumen:

\[\int_{\textrm{V}} [\nabla \cdot \textbf{J}_{f} + \frac{\partial \rho f}{\partial t}] d \textrm{V} = 0 \Rightarrow \nabla \cdot \textbf{J}_{f} + \frac{\partial \rho_{f}}{\partial t} = 0 \nonumber \]

donde se obtiene la forma de punto diferencial ya que la integral debe ser verdadera para cualquier volumen de manera que el término entre corchetes debe ser cero en cada punto. De la ley de Gauss (\(\nabla \codt \textbf{D} = \rho_{f}\)) (8) y (9) también se puede escribir como

\[\oint_{S}(\textbf{J}_{f} + \frac{\partial \textbf{D}}{\partial t}) \cdot \textbf{dS} = 0, \: \: \: \nabla \cdot (\textbf{J}_{f} + \frac{\partial \textbf{D}}{\partial t}) = 0 \nonumber \]

donde _Jf se denomina densidad de corriente de conducción y\(\partial \textbf{D} / \partial t\) se denomina densidad de corriente de desplazamiento.

Esta es la forma de campo de la ley de corriente de circuito de Kirchoff que la suma algebraica de corrientes en un nodo suma a cero. La ecuación (10) nos dice de manera equivalente que el flujo neto de la corriente total, conducción más desplazamiento, es cero por lo que toda la corriente que ingresa a una superficie debe abandonarla. La corriente de desplazamiento no implica ningún transporte de carga para que la corriente variable en el tiempo se pueda transmitir a través del espacio sin portadores de carga. En condiciones estáticas, la corriente de desplazamiento es cero.

Modelos de conducción de gas cargado

a) Ecuaciones Gobernantes. En muchos materiales, incluyendo buenos conductores como metales, gases ionizados y soluciones electrolíticas, así como conductores más pobres como aisladores con pérdida y semiconductores, los portadores de carga pueden modelarse clásicamente como un gas ideal dentro del medio, llamado plasma. Suponemos que tenemos dos portadores de igual magnitud pero signo opuesto\(\pm q\) con respectivas masas\(m_{\pm}\) y densidades numéricas\(n_{\pm}\). Estas cargas pueden ser huecos y electrones en un semiconductor, iones con carga opuesta en una solución electrolítica, o electrones y núcleos en un metal. Cuando se aplica un campo eléctrico, las cargas positivas se mueven en la dirección del campo mientras que las cargas negativas se mueven en la dirección opuesta. Estas cargas chocan con el medio anfitrión a frecuencias respectivas\(\nu_{+}\) y\(\nu_{-}\), que luego actúan como una disipación viscosa o friccional opuesta al movimiento. Además de las fuerzas eléctricas y de fricción, las partículas ejercen una fuerza sobre sí mismas a través de un término de presión debido a la agitación térmica que estaría presente incluso si las partículas estuvieran descargadas. Para un gas ideal la presión parcial p es

\[p = nkT \textrm{ pascals }[\textrm{kg s}^{-2} \cdot \textrm{m}^{-1}] \nonumber \]

donde n es la densidad numérica de cargas, T es la temperatura absoluta, y\(k = 1.38 \times 10^{-23} \textrm{joule}/^{\circ}K\) se llama constante de Boltzmann.

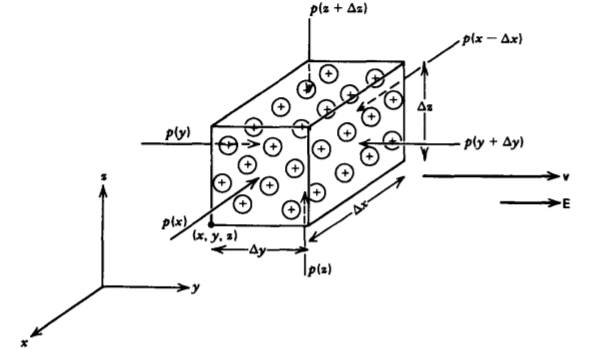
La fuerza de presión neta sobre el pequeño volumen rectangular mostrado en la Figura 3-10 es

\[\textbf{f}_{p} = (\frac{p(x - \Delta x) - p (x)}{\Delta x} \textbf{i}_{x} + \frac{p(y) - p(y + \Delta y)}{\Delta y} \textbf{i}_{y} \\ + \frac{p(z) - p(z + \Delta z)}{\Delta z} \textbf{i}_{z}) \Delta x \Delta y \Delta z \nonumber \]

donde vemos que la presión sólo ejerce una fuerza neta sobre el volumen si es diferente en cada superficie opuesta. A medida que el volumen se contrae a un tamaño infinitesimal, los términos de presión en (12) definen derivadas parciales de modo que la densidad de fuerza volumétrica se vuelve

\[\lim_{\Delta x \rightarrow 0 \\ \Delta y \rightarrow 0 \\ \Delta z \rightarrow 0} \frac{\textbf{f}_{p}}{\Delta x \Delta y \Delta z} = -(\frac{\partial p}{\partial x} \textbf{i}_{x} + \frac{\partial p}{\partial y} \textbf{i}_{y} + \frac{\partial p}{\partial z} \textbf{i}_{z}) = - \nabla p \nonumber \]

Luego usando (11) - (13), la ley de fuerza de Newton para cada portador de carga dentro del pequeño volumen es

\[m_{\pm} \frac{\partial \textbf{v}_{\pm}}{\partial t} = \pm q \textbf{E} - m_{\pm} \nu_{\pm} \textbf{v}_{\pm} - \frac{1}{n_{\pm}} \nabla (n_{\pm} kT) \nonumber \]

Figura 3-10 Ley de fuerza de Newton, aplicada a un pequeño volumen rectangular que se\(\Delta x \: \Delta y \: \Delta z\) mueve con velocidad v, encerrando cargas positivas con densidad numérica n. La presión es la fuerza por unidad de área que actúa normalmente hacia adentro en cada superficie y solo contribuye a la fuerza neta si es diferente en caras opuestas.

donde el campo eléctrico E se debe al campo impuesto más el campo generado por las cargas, según lo dado por la ley de Gauss.

b) Conducción por Difusión a la Derivación

Debido a que en muchos materiales las frecuencias de colisión son típicamente del orden de\(\nu \approx 10^{13} \textrm{Hz}\), los términos de inercia en (14) a menudo son insignificantes. En este límite podemos resolver fácilmente (14) para la velocidad de cada portador como

\[\lim_{\partial \textbf{v}_{\pm}/\partial t << \nu_{\pm} \textbf{v}_{\pm}} \textbf{v}_{\pm} = \frac{1}{m_{\pm} \nu_{\pm}} ( \pm q \textbf{E} - \frac{1}{n_{\pm}} \nabla (n_{\pm}kT)) \nonumber \]

La carga y la densidad de corriente para cada portador se dan simplemente como

\[\rho_{\pm} = \pm qn_{\pm}, \: \: \: \textbf{J}_{\pm} = \rho_{\pm}\textbf{v}_{\pm} = \pm q n_{\pm}\textbf{\pm} \nonumber \]

Multiplicando (15) por las densidades de carga entonces nos da la ley constitutiva para cada corriente como

\[\textbf{J}_{\pm} = \pm qn_{\pm}\textbf{v}_{\pm} = \pm \rho_{\pm} \mu_{\pm}\textbf{E} - D_{\pm} \nabla \rho_{\pm} \nonumber \]

donde\(\mu_{\pm}\) se llaman las movilidades de las partículas y\(D_{\pm}\) son sus coeficientes de difusión

\[\mu_{\pm} = \frac{q}{m_{\pm}\nu_{\pm}} [\textrm{A kg}^{-1} \cdot \textrm{s}^{-2}], \: \: \: D_{\pm} = \frac{kT}{m_{\pm}\nu_{pm}}[\textrm{m}^{2} \cdot \textrm{s}^{-1}] \nonumber \]

asumiendo que el sistema se encuentra a temperatura constante. Vemos que la relación\(D_{\pm}/\mu_{\pm}\) para cada portadora es la misma teniendo unidades de voltaje, así llamado el voltaje térmico:

\[\frac{D_{\pm}}{\mu_{\pm}} = \frac{kT}{q} \textrm{volts} [ \textrm{kg m}^{2} \cdot \textrm{A}^{-1} \cdot \textrm{s}^{-3}] \nonumber \]

Esta igualdad se conoce como la relación de Einstein.

En equilibrio cuando la corriente neta de cada portadora es cero, (17) puede escribirse en términos del potencial como (\(\textbf{E} = - \nabla V\))

\[\textbf{J}_{+} = \textbf{J}_{-} = 0 = - \rho_{\pm} \mu_{\pm} \nabla V \mp D_{\pm} \nabla \rho_{\pm} \nonumber \]

que se puede reescribir como

\[\nabla [\pm \frac{\mu_{\pm}}{D_{\pm}} V + \ln \rho_{\pm}]=0 \nonumber \]

El término entre corchetes solo puede ser una constante, por lo que la densidad de carga está relacionada con el potencial por la distribución de Boltzmann:

\[\rho_{\pm} = \pm \rho_{0} e^{\mp qV/kT} \nonumber \]

donde usamos la relación Einstein de (19) y\(\pm \rho_{0}\) es la densidad de carga de equilibrio de cada portador cuando V =0 y son de igual magnitud porque el sistema es inicialmente neutro.

Para encontrar la dependencia espacial de\(\rho\) y V usamos (22) en la ecuación de Poisson derivada en la Sección 2.5.6:

\[\nabla^{2}V = - \frac{(\rho_{+} + \rho_{-})}{\varepsilon} = - \frac{\rho_{0}}{\varepsilon}(e^{-qV}{kT}-e^{qV/kT})= \frac{2 \rho_{0}}{\varepsilon} \sinh \frac{qV}{kT} \nonumber \]

Esta ecuación se conoce como la ecuación de Poisson-Boltzmann porque las densidades de carga obedecen a las distribuciones de Boltzmann.

Considere un electrodo colocado a x = 0 elevado al potencial\(V_{0}\) con respecto a un potencial cero a\(x = \pm \infty\), como en la Figura 3-11 a. Debido a que el electrodo es largo, el potencial solo varía

Figura 3-11 Las cargas móviles de polaridad opuesta se acumulan alrededor de cualquier carga neta insertada en un conductor descrito por las ecuaciones de deriva y difusión, y tienden a proteger su campo para distancias mayores que la longitud de Debye. (a) Electrodo a potencial V _o con respecto a un potencial cero at\(x = \pm \infty\). La desintegración espacial es más rápida para valores mayores de V _o. b) Cargo puntual.

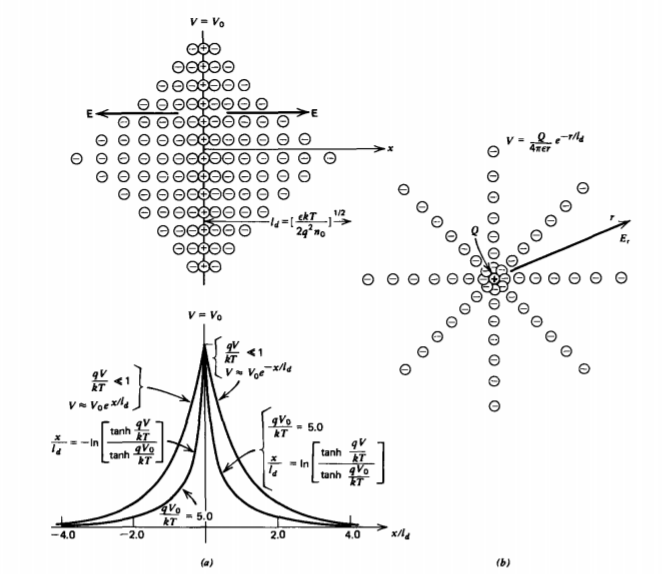
con la coordenada x para que (23) se convierta

\[\frac{d^{2}\tilde{V}}{dx^{2}} - \frac{1}{l^{2}_{d}} \sinh \tilde{V} = 0, \: \: \: \tilde{V} = \frac{qV}{kT}, \: \: \: l_{d}^{2}= \frac{\varepsilon kT}{2 \rho_{0}q} \nonumber \]

donde normalizamos el voltaje al voltaje térmico kt/q y l _d se llama longitud Debye.

Si (24) se multiplica por DV/dx, se puede escribir como un diferencial exacto:

\[\frac{d}{dx}[\frac{1}{2}(\frac{d \tilde{V}}{dx})^{2} - \frac{\cosh \tilde{V}}{l_{d}^{2}}] = 0 \nonumber \]

El término entre corchetes debe ser entonces una constante que se evalúe lejos del electrodo donde el potencial y el campo eléctrico\(\tilde{E} = -d \tilde{V}/dx\) son cero:

\[\frac{d \tilde{V}}{dx} = - \tilde{E}_{x} = [\frac{2}{l^{2}_{d}} (\cosh \tilde{V} -1)]^{1/2} = \mp \frac{2}{l_{d}} \sinh \frac{\tilde{V}}{2} \left \{ \begin{matrix} x>0 \\ x<0 \end{matrix} \right. \nonumber \]

Los diferentes signos tomados con la raíz cuadrada son necesarios porque el campo eléctrico apunta en direcciones opuestas a cada lado del electrodo. El potencial se encuentra entonces implícitamente por la integración directa como

\[\frac{\tanh (\tilde{V}/4)}{\tanh (\tilde{V}_{0}/4)} = e^{\mp x/l_{d}} \left \{ \begin{matrix} x>0 \\ x<0 \end{matrix} \right. \nonumber \]

La longitud de Debye describe así la longitud característica sobre la cual el potencial aplicado ejerce influencia. En muchos materiales la densidad numérica de portadores es fácilmente del orden de\(n_{0} \approx 10^{20}/m^{3}\), por lo que a temperatura ambiente (\(T \approx 293^{\circ}K\)), l _d es típicamente de 10 ^-7 m.

Muchas veces los potenciales son muy pequeños así que eso\(qv/kT<<1\). Entonces, los términos hiperbólicos en (27), así como en la ecuación gobernante de (23), pueden aproximarse por sus argumentos:

\[\nabla^{2}V - \frac{V}{l^{2}_{d}} =0 \nonumber \]

Esta aproximación sólo es válida cuando los potenciales son mucho menores que el voltaje térmico\(kt/q\), que, a temperatura ambiente es de aproximadamente 25 mv. En este límite la solución de (27) muestra que la distribución de voltaje disminuye exponencialmente. A valores más altos de Vo, el decaimiento es más rápido, como se muestra en la Figura 3-11 a.

Si se inserta una carga puntual Q en el medio plasmático, como en la Figura 3-11 b, el potencial solo depende de la distancia radial r. En el pequeño límite de potencial, (28) en las coordenadas esféricas es

\[\frac{1}{r^{2}} \frac{\partial}{\partial r} (r^{2} \frac{\partial V}{\partial r}) - \frac{V}{l_{d}^{2}} = 0 \nonumber \]

Al darse cuenta de que esta ecuación se puede reescribir como

\[\frac{\partial^{2}}{\partial r^{2}} (rV) - \frac{(rV)}{l_{d}^{2}}=0 \nonumber \]

tenemos una ecuación diferencial de coeficiente constante lineal en la variable (rV) para la cual las soluciones son

\[rV = A_{1} e^{-r/l_{d}}+ A_{2}e^{+r/l_{d}} \nonumber \]

Porque el potencial debe decaer y no crecer lejos de la carga,\(A_{2}=0\) y la solución es

\[V= \frac{Q}{4 \pi \varepsilon r} e^{-r/l_{d}} \nonumber \]

donde evaluamos\(A_{1}\) al darnos cuenta de que como\(r \rightarrow 0\) el potencial debe acercarse al de una carga puntual aislada. Tenga en cuenta que para r pequeños el potencial se vuelve muy grande y se viola la aproximación de potencial pequeño.

(c) Ley de Ohm

Hemos visto que las cargas móviles en un sistema descrito por las ecuaciones de deriva y difusión acumulan carga de polaridad casi opuesta y tienden a blindar su efecto para distancias mayores que la longitud de Debye. Debido a que esta distancia suele ser mucho menor que las dimensiones características del sistema, la mayoría de las regiones del espacio fuera de la vaina de Debye son neutras de carga con cantidades iguales de densidad de carga positiva y negativa\(\pm \rho_{0}\). En esta región, el término de difusión en (17) es despreciable porque no hay gradientes de densidad de carga. Entonces la densidad de corriente total es proporcional al campo eléctrico:

\[\textbf{J} = \textbf{J}_{+} + J_{-} = \rho_{0}(\textbf{v}_{+} - \textbf{v}_{-}) = qn_{0}(\mu_{+} + \mu_{-}) \textbf{E} = \sigma \textbf{E} \nonumber \]

donde\(\sigma\) [siemans/m (m ^-3 kg ^-1 s ³ A ²)] se llama la conductividad óhmica y (33) es la forma puntual de la ley de Ohm. A veces es más conveniente trabajar con la conductividad recíproca\(\rho_{r} = (1/\rho)\) (ohm-m) llamada resistividad. Utilizaremos predominantemente la ley de Ohm para describir la mayoría de los medios en este texto, pero es importante recordar que a menudo no es válida dentro de las pequeñas distancias de Debye cercanas a las cargas. Cuando la ley de Ohm es válida, la carga neta es cero, por lo que no da ninguna contribución a la ley de Gauss. En el Cuadro 3-2 se enumeran las conductividades óhmicas para diversos materiales. Vemos que diferentes materiales varían en amplios rangos en su capacidad para realizar cargos.

La conductividad óhmica de los “conductores perfectos” es grande y está idealizada para ser infinita. Dado que todas las corrientes físicas en (33) deben permanecer finitas, el campo eléctrico dentro del conductor es cero de manera que impone una superficie equipotencial:

\[\lim_{\sigma \rightarrow \infty} \textbf{J} = \sigma \textbf{E} \Rightarrow \left \{ \begin{matrix} \textbf{E} = 0 \\ V = \textrm{const} \\ \textbf{J} = \textrm{finite} \end{matrix} \right. \nonumber \]

Tabla 3-2 La conductividad óhmica para diversas sustancias comunes a temperatura ambiente

	\(\sigma\)[siemen/m]
Plata ^a	6.3 x 10 ^7
Cobre ^a	5.9 x 10 ^7
Oro ^a	4.2 x 10 ^7
Liderar ^un	0.5 x 10 ^7
Estaño ^a	0.9 x 10 ^7
Zinc ^a	1.7 x 10 ^7
Carbono ^a	7.3 x 10 ^-4
Mercurio ^b	1.06 x 10 ^6
Agua Pura ^b	4 x 10 ^-6
Nitrobenceno ^b	5 x 10 ^-7
Metanol ^b	4 x 10 ^-5
Etanol ^b	1.3 x 10 ^-7
Hexano ^b	<1 x 10 ^-18

^a De Handbook of Chemistry and Physics, 49a ed., The Chemical Rubber Co., 1968, p. E80.

^b De Lange's Handbook of Chemistry, 10a ed., McGraw-Hill, Nueva York, 1961, pp. 1220-21.

A lo largo de este texto, generalmente se supone que los electrodos son perfectamente conductores y por lo tanto están a un potencial constante. El campo eléctrico externo debe entonces ser incidente perpendicularmente a la superficie

d) Superconductores

Una excepción notable a la ley de Ohm es para materiales superconductores a temperaturas criogénicas. Entonces, con colisiones despreciables (\(\nu_{\pm} = 0\)) y la temperatura absoluta baja (\(T \approx 0\)), la fuerza eléctrica sobre las cargas solo se equilibra por su inercia de manera que (14) se vuelve simplemente

\[\frac{\partial \textbf{V}_{\pm}}{\partial t} = \pm \frac{q}{m_{\pm}} \textbf{E} \nonumber \]

Multiplicamos (35) por las densidades de carga que suponemos que son constantes para que la ley constitutiva que relaciona la densidad de corriente con el campo eléctrico sea

\[\frac{\partial (\pm qn_{\pm} \textbf{v}_{\pm})}{\partial t} = \frac{\partial \textbf{J}_{\pm}}{\partial t} = \frac{q^{2}n_{\pm}}{m_{\pm}} \textbf{E} = \omega^{2}_{p_{\pm}} \varepsilon \textbf{E}, \: \: \: \omega^{2}_{p_{\pm}} = \frac{q^{2}n_{pm}}{m_{\pm}\varepsilon} \nonumber \]

donde\(\omega_{p \pm}\) se llama la frecuencia de plasma para cada portadora.

Para electrones (q = -1.6 x 10 ^-19 coul, m_ = 9.1 x 10 ^-31 kg) de densidad\(n_{-} \approx 10^{20}/m^{3}\) dentro de un material con la permitividad del espacio libre,\(\varepsilon = \varepsilon_{0} \approx 8.854 \times 10^{-12}\) farad/m, la frecuencia plasmática es

\[\omega_{p_{-}} = \sqrt{q^{2}n_{-}/m_{- \varepsilon}} \approx 5.6 \times 10^{11} \textrm{ radian/sec} \\ \Rightarrow f_{p_{-}} = \omega_{p_{-}}/2 \pi \approx 9 \times 10^{10} \textrm{Hz} \nonumber \]

Si dicho material se coloca entre electrodos de placa paralelos que están en circuito abierto, el campo eléctrico y la densidad de corriente J = J ₊ J _ deben ser perpendiculares a los electrodos, los cuales tomamos como dirección x. Si el espaciamiento de electrodos es pequeño en comparación con el ancho, los campos interelectrodos lejos de los extremos deben ser dirigidos x y ser solo una función de x. Entonces la derivada de tiempo de la ecuación de conservación de carga en (10) es

\[\frac{\partial}{\partial x} [ \frac{\partial}{\partial t} (J_{+} + J_{-}) + \varepsilon \frac{\partial^{2}E}{\partial t^{2}}]=0 \nonumber \]

El término entre corchetes es solo la derivada de tiempo de la densidad de corriente total, que es cero debido a que los electrodos están en circuito abierto de modo que usar (36) en (38) rinde

\[\frac{\partial^{2}E}{\partial t^{2}} + \omega^{2}_{p} E = 0, \:\: \: \omega^{2}_{p} = \omega^{2}_{p +} + \omega^{2}_{p -} \nonumber \]

que cuenta con soluciones

\[E = A_{1} \sin \omega_{p}t + A_{2} \cos \omega_{p}t \nonumber \]

Cualquier perturbación inicial provoca un campo eléctrico oscilatorio a la frecuencia de plasma compuesto w,. Las cargas luego ejecutan un simple movimiento armónico sobre su posición de equilibrio.