3.3: Condiciones de límites de campo

En muchos problemas hay una superficie de discontinuidad que separa materiales diferentes, como entre un conductor y un dieléctrico, o entre diferentes dieléctricos. Debemos determinar cómo cambian los campos a medida que cruzamos la interfaz donde las propiedades del material cambian abruptamente

Componente tangencial de E

Aplicamos la línea integral del campo eléctrico alrededor de un contorno de tamaño diferencial que encierra la interfaz entre materiales disímiles, como se muestra en la Figura 3-12 a. Las secciones largas a y c de longitud dl son tangenciales a la superficie y las secciones de unión cortas b y d son de longitud cero ya que se supone que la interfaz tiene espesor cero. Aplicando la línea integral del campo eléctrico alrededor de este contorno, a partir de la Sección 2.5.6 obtenemos

\[\oint_{L} \textbf{E} \cdot \textbf{dl} = (E_{1t} - E_{2t}) dl = 0 \nonumber \]

donde E _{1 t} y E _{2 t} son los componentes del campo eléctrico tangencial a la interfaz. No obtenemos ninguna contribución de los componentes normales de campo a lo largo de las secciones b y d porque las longitudes de contorno son cero. El signo menos surge a lo largo de c porque el campo eléctrico está en la dirección opuesta al recorrido del contorno. Tenemos así que la tangencial

Figura 3-12 (a) La ley de Stokes aplicada a una línea integral alrededor de una interfaz de discontinuidad muestra que el componente tangencial del campo eléctrico es continuo a través del límite. (b) La ley de Gauss aplicada a un volumen de caja de paletas que se extiende a ambos lados de la interfaz muestra que el componente normal del vector de desplazamiento es discontinuo en la densidad de carga superficial libre\(\sigma_{f}\).

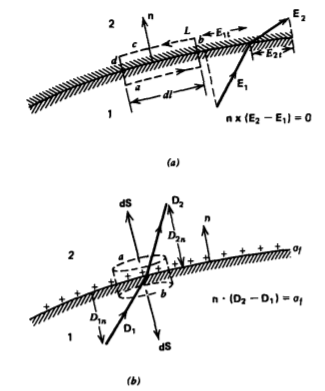
los componentes del campo eléctrico son continuos a través de la interfaz

\[E_{1t} = E_{2t} \Rightarrow \textbf{n} \times (\textbf{E}_{2} - \textbf{E}_{1}) =0 \nonumber \]

donde n es la normal interfacial mostrada en la Figura 3-12 a.

Dentro de un conductor perfecto el campo eléctrico es cero. Por lo tanto, a partir de (2) sabemos que el componente tangencial de E fuera del conductor también es cero. Así, el campo eléctrico siempre debe terminar perpendicularmente a un conductor perfecto

Componente Normal de D

Generalizamos los resultados de la Sección 2.4.6 para incluir medios dieléctricos al elegir nuevamente una pequeña superficie gaussiana cuyas superficies superior e inferior de área dS son paralelas a una interfaz de carga superficial y están unidas por una superficie cilíndrica infinitamente delgada con área cero, como se muestra en la Figura 3-12b. Entonces solo las caras a y b contribuyen a la ley de Gauss:

\[\oint_{S} \textbf{D} \cdot \textbf{dS} = (D_{2n} -D_{1n}) d \textbf{S} = \oint_{f} d \textbf{S} \nonumber \]

donde la interfaz soporta una densidad de carga superficial libre\(sigma_{f}\) y\(D_{2n}\) y\(D_{1n}\) son los componentes del vector de desplazamiento a cada lado de la interfaz en la dirección de la normal n mostrada, apuntando de la región 1 a la región 2. Reduciendo (3) y usando notación más compacta tenemos

\[D_{2n} -D_{1n} = \sigma_{f}, \: \: \: \textbf{n} \cdot (\textbf{D}_{2} - \textbf{D}_{1}) = \sigma_{f} \nonumber \]

donde surge el signo menos frente a D ₁ porque la normal en la superficie inferior b es - n. Los componentes normales del vector de desplazamiento son discontinuos si la interfaz tiene una densidad de carga superficial. Si no hay carga superficial (\(\sigma_{f} = 0\)), los componentes normales de D son continuos. Si cada medio no tiene polarización, (4) reduce a los resultados de espacio libre de la Sección 2.4.6.

En la interfaz entre dos dieléctricos sin pérdidas diferentes, generalmente no hay carga superficial (\(\sigma_{f} =0\)), a menos que se haya colocado deliberadamente, porque sin conductividad no hay corriente para transportar carga. Entonces, aunque el componente normal del campo D es continuo, el componente normal del campo eléctrico es discontinuo porque la constante dieléctrica en cada región es diferente.

En la interfaz entre diferentes materiales conductores, puede existir carga superficial libre ya que la corriente puede transportar carga a la discontinuidad superficial. Generalmente para tales casos, la densidad de carga superficial es distinta de cero. En particular, si una región es un conductor perfecto con cero campo eléctrico interno, la densidad de carga superficial en la superficie es igual a la componente normal del campo D en la superficie del conductor,

\[\sigma_{f} = \textbf{n} \cdot \textbf{D} \nonumber \]

donde n es la normal saliente del conductor perfecto.

Carga puntual por encima de un límite dieléctrico

Si una carga puntual q dentro de una región de permitividad\(\varepsilon_{1}\) es una distancia d por encima de un límite plano que separa la región I de la región II con permitividad\(\varepsilon_{2}\), como en la Figura 3-13, el componente tangencial de E y en ausencia de carga superficial libre el componente normal de D, debe ser continuo a través de la interfaz. Intentemos utilizar el método de las imágenes colocando una carga de imagen q' en y = -d para que la solución en la región I se deba a esta carga de imagen más la carga puntual original q. La solución para el campo en la región II se debe a una carga de imagen q” en y = d, la posición de la carga puntual original. Tenga en cuenta que la carga de imagen apropiada siempre está fuera de la región donde se desea la solución. En este punto no sabemos si es posible satisfacer las condiciones de contorno con estos cargos de imagen, pero trataremos de encontrar valores de q' y q” para hacerlo.

Figura 3-13 (a) Una carga puntual q por encima de un límite dieléctrico plano requiere diferentes conjuntos de cargas de imagen para resolver para los campos en cada región. (b) El campo en la región I se debe a la carga original y a la carga de imagen q' mientras que el campo en la región II se debe únicamente al cargo de imagen q”.

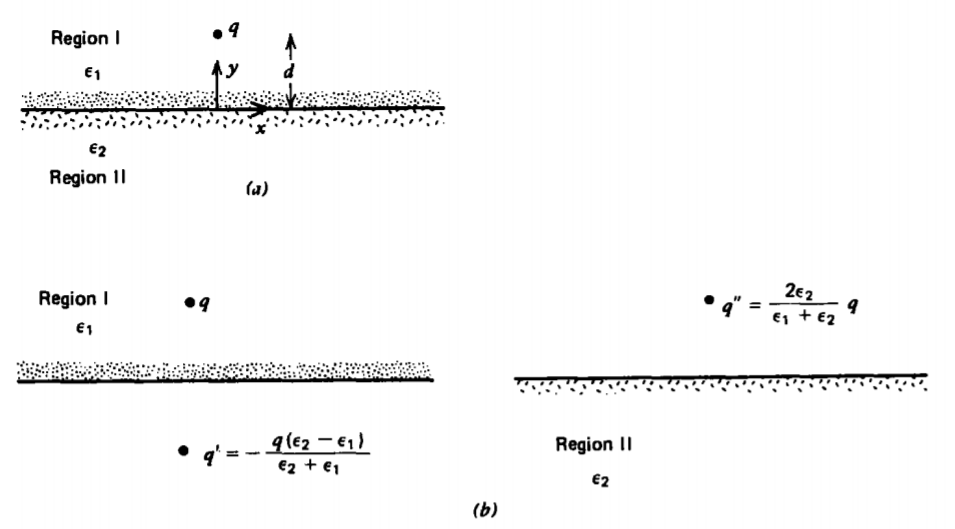
El potencial en cada región es

\[V_{I} = \frac{1}{4 \pi \varepsilon_{1}} (\frac{q}{[x^{2} + (y-d)^{2} + z^{2}]^{1/2}} + \frac{q'}{[x^{2} + (y + d)^{2} + z^{2}]^{1/2}}), \: \: y \leq 0 \\ V_{II} = \frac{1}{4 \pi \varepsilon_{2}} \frac{q"}{[x^{2} + (y-d)^{2} + z^{2}]^{1/2}}, \: \: \: y \leq 0 \nonumber \]

con campo eléctrico resultante

\[E_{I} = - \nabla V_{I} \\ = \frac{1}{4 \pi \varepsilon_{1}} (\frac{q[x \textbf{i}_{x} + (y-d) \textbf{i}_{y} + z \textbf{i}_{z}]}{[x^{2} + (y-d)^{2} + z^{2}]^{3/2}} + \frac{q' [x \textbf{i}_{z} + (y+d) \textbf{i}_{y} + z \textbf{i}_{z}]}{[x^{2} + (y + d)^{2} + z^{2}]^{3/2}}) \\ \textbf{E}_{II} = - \nabla V_{II} = \frac{q"}{4 \pi \varepsilon_{2}} (\frac{x \textbf{i}_{x} + (y-d) \textbf{i}_{y} + z \textbf{i}_{z}}{[x^{2} + (y-d)^{2} + z^{2}]^{3/2}}) \nonumber \]

Para satisfacer la continuidad del campo eléctrico tangencial a y =0 tenemos

\[\left. \begin{matrix} E_{x1} = E_{xII} \\ \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: & \Rightarrow \frac{q+q'}{\varepsilon_{1}} = \frac{q"}{\varepsilon_{2}} \\ E_{zI} = E_{zII} \end{matrix} \right. \nonumber \]

Sin carga superficial, el componente normal de D debe ser continuo a y = 0,

\[\varepsilon_{1}E_{yI} = \varepsilon_{2}E_{yII} \Rightarrow -q + q' = -q" \nonumber \]

Resolviendo (8) y (9) para los cargos desconocidos que encontramos

\[q' = -\frac{(\varepsilon_{2}-\varepsilon_{1})}{\varepsilon_{1} + \varepsilon_{2}}q \\ q" = \frac{2 \varepsilon_{2}}{(\varepsilon_{1} + \varepsilon_{2})}q \nonumber \]

La fuerza sobre la carga puntual q se debe únicamente al campo de la carga de imagen q':

\[\textbf{f} = \frac{qq'}{4 \pi \varepsilon_{1}(2d)^{2}}\textbf{i}_{y} = - \frac{q^{2} (\varepsilon_{2} - \varepsilon_{1})}{16 \pi \varepsilon_{1}(\varepsilon_{1} + \varepsilon_{2})d^{2}}\textbf{i}_{y} \nonumber \]

Componente Normal de P y\(\varepsilon_{0}E\)

Al integrar el flujo de polarización sobre la misma superficie gaussiana del pastillero, mostrado en la Figura 3-12 b, relacionamos la discontinuidad en la componente normal de polarización con la densidad de carga de polarización superficial\(\sigma_{p}\) usando las relaciones de la Sección 3.1.2:

\[\oint_{S} \textbf{P} \cdot \textbf{dS} = - \int_{S} \sigma_{p} dS \Rightarrow P_{2n} - P_{1n} = - \sigma_{p} \Rightarrow \textbf{n} \cdot (\textbf{P}_{2}- \textbf{P}_{1}) = - \sigma_{p} \nonumber \]

El signo menos delante de\(\sigma_{p}\), resulta debido al signo menos que relaciona la densidad de carga de polarización volumétrica con la divergencia de P.

Para resumir, la carga de polarización es la fuente de P, la carga gratuita es la fuente de D, y la carga total es la fuente de\(\varepsilon_{0}\textbf{E}\). Usando (4) y (12), la discontinuidad interfacial del campo eléctrico es

\[\textbf{n} \cdot (\textbf{E}_{2} - \textbf{E}_{1}) = \frac{\textbf{n} \cdot [(\textbf{D}_{2}-\textbf{D)_{1})-(\textbf{P}_{2}-\textbf{P}_{1})]}{\varepsilon_{0}} = \frac{\sigma_{f} + \sigma_{p}}{\varepsilon_{0}} \nonumber \]

Para los dieléctricos lineales suele ser conveniente agrupar los efectos de polarización en la permitividad\(\varepsilon\) y nunca usar el vector P, solo D y E.

Para materiales polarizados permanentemente, suele ser conveniente reemplazar la polarización P por la densidad de carga volumétrica de polarización equivalente y densidad de carga superficial de (12) y resolver para E usando la integral de superposición culómbica de la Sección 2.3.2. En muchos problemas dieléctricos, no hay carga de polarización de volumen, pero en las superficies de discontinuidad está presente una carga de polarización superficial según lo dado por (12).

Ejemplo 3-2: Cilindro permanentemente polarizado a lo largo de su eje

Un cilindro de radio a y altura L está centrado alrededor del eje z y tiene una polarización uniforme a lo largo de su eje, P =\(P_{0}\textbf{i}_{z}\), como se muestra en la Figura 3-14. Encuentra el campo eléctrico E y el vector de desplazamiento D en todas partes en su eje.

Solución

Con una polarización constante P, la densidad de carga de polarización de volumen es cero:

\(\rho_{p} = - \nabla \cdot \textbf{P} = 0\)

Puesto que P =0 fuera del cilindro, el componente normal de P es discontinuo en las superficies superior e inferior produciendo cargas uniformes de polarización superficial:

\(\sigma_{p} (z = L/2)=P_{0}, \: \: \: \sigma_{P}(z = -L/2) = -P_{0}\)

Figura 3-14 (a) El campo eléctrico debido a un cilindro uniformemente polarizado de longitud L es el mismo que para dos discos de carga superficial de polaridad opuesta\(\pm P_{0}\) z = L /2. (b) El campo de desplazamiento perpendicular\(D_{z}\) es continuo a través de las interfaces\(z = \pm L/2\) mientras que el campo eléctrico\(E_{z}\) es discontinuo.

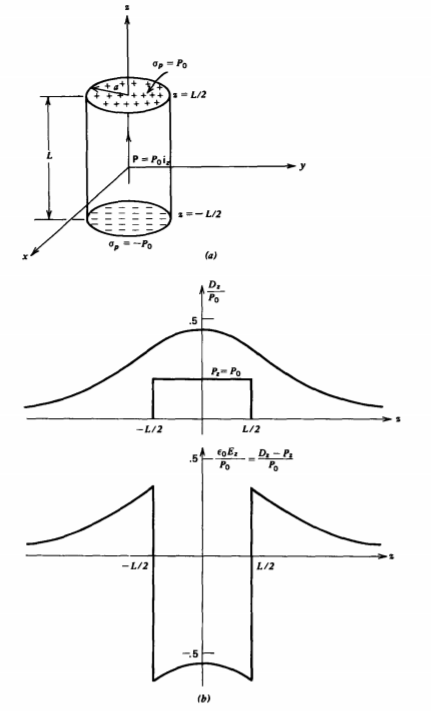
La solución para un solo disco de carga superficial se obtuvo en la Sección 2.3.5b. Superponemos los resultados para los dos discos teniendo cuidado de desplazar la distancia axial de manera apropiada,\(\pm L/2\) dando la solución concisa para el campo de desplazamiento:

\(D_{z} = \frac{P_{0}}{2} (\frac{(z + L/2)}{[a^{2} + (z + L/2)^{2}]^{1/2}} - \frac{(z-L/2)}{[a^{2} + (z-L/2)^{2}]^{1/2}})\)

El campo eléctrico es entonces

\(E_{z} = \left \{ \begin{matrix} D_{z}/\varepsilon_{0}, & \vert z \vert L/2 \\ (D_{z}-P_{0})/\varepsilon_{0} & \vert z \vert < L/2 \end{matrix} \right.\)

Estos resultados pueden ser examinados en diversos límites. Si el radio a llega a ser muy grande, el campo eléctrico debe aproximarse al de dos láminas paralelas de carga superficial\(\pm P_{0}\), como en la Sección 2.3.4b:

\(\lim_{a \rightarrow \infty} E_{z} = \left \{ \begin{matrix} 0, & \vert z \vert L/2 \\ -P_{0}/\varepsilon_{0}, & \vert z \vert < L/2 \end{matrix} \right.\)

con un campo de desplazamiento cero en todas partes.

En el límite opuesto, para z grande (z >> a, z >>L) lejos del cilindro, el campo eléctrico axial muere como el campo dipolo con\(\theta = 0\)

\(\lim_{z \rightarrow \infty} E_{z} = \frac{p}{2 \pi \varepsilon_{0}z^{3}}, \: \: \: p = P_{0} \pi a^{2}L\)

con momento dipolo efectivo p dado por el producto de la carga de polarización total en\(z = L/2, \: (P_{0} \pi a^{2})\), y la longitud L.

Componente Normal de J

Aplicar la conservación de la ecuación de corriente total en la Sección 3.2.1 a la misma superficie de pastillero gaussiano en la Figura 3-12 b da como resultado contribuciones nuevamente solo de las superficies superior e inferior etiquetadas como "a" y "b”

\[\textbf{n} \cdot (\textbf{J}_{2} - \textbf{J}_{1} + \frac{\partial}{\partial t} (\textbf{D}_{2} - \textbf{D}_{1}))=0 \nonumber \]

donde asumimos que no fluyen corrientes superficiales a lo largo de la interfaz. A partir de (4), relacionando la densidad de carga superficial con la discontinuidad en D normal, esta condición límite también se puede escribir como

\[\textbf{n} \cdot (\textbf{J}_{2} - \textbf{J}_{1}) + \frac{\partial \sigma_{f}}{\partial t} = 0 \nonumber \]

lo que nos dice que si la corriente que entra en una superficie es diferente de la corriente que sale, la carga se ha acumulado en la interfaz. En el estado estacionario de CC, el componente normal de J es continuo a través de un límite.