3.4: Resistencia

Resistencia entre dos electrodos

Dos conductores mantenidos a una diferencia de potencial V dentro de un medio conductor pasarán cada uno una corriente total I, como se muestra en la Figura 3-15. Al aplicar la forma integral superficial de conservación de carga en la Sección 3.2.1 a una superficie S' que rodea ambos electrodos pero está lo suficientemente lejos para que J y D sean insignificantes pequeñas, vemos que las únicas contribuciones de corriente distintas de cero son de los cables terminales que pasar a través de la superficie. Estos deben sumar a cero para que las corrientes tengan magnitudes iguales pero fluyan en direcciones opuestas. De igual manera, aplicar conservación de carga a una superficie S que encierra el electrodo superior muestra que la corriente I que ingresa al electrodo a través del cable debe ser igual a la corriente total (conducción más desplazamiento) que sale del electrodo. Esta corriente total viaja al electrodo opuesto y sale a través del cable de conexión.

Figura 3-15 Un voltaje aplicado a través de dos electrodos dentro de un medio óhmico hace que una corriente fluya hacia un electrodo y salga del otro. Los electrodos tienen igual magnitud pero cargas de polaridad opuesta de manera que a lo lejos los campos mueren como un dipolo\(\alpha (1/r^{3})\). Entonces, a pesar de que la superficie S' está aumentando como\(r^{2}\), el flujo de corriente va a cero como 1/r.

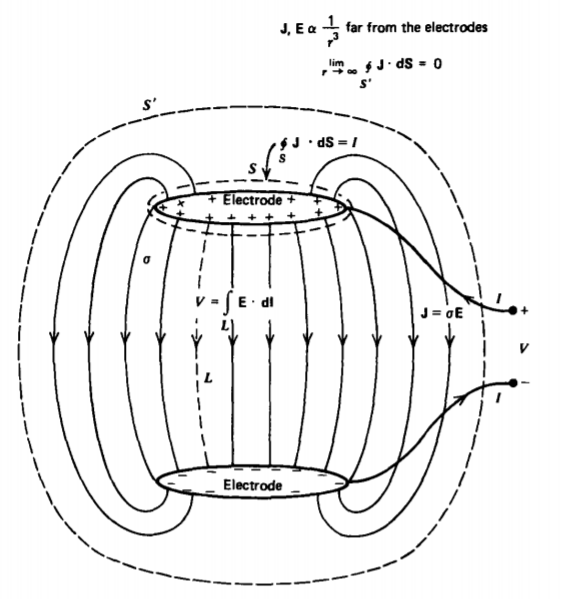
La relación de voltaje a corriente continua en estado estacionario entre los dos electrodos en la Figura 3-15 se define como la resistencia:

\[\textrm{R} = \frac{V}{I} \textrm{ohm}[ \textrm{kg m}^{2} \textrm{s}^{-3} \textrm{A}^{-2}] \label{eq1} \]

Para una geometría arbitraria, la ecuación\ ref {eq1} se puede expresar en términos de los campos como

\[\textrm{R} = \frac{\int_{L} \textbf{E} \cdot \textbf{dl}}{\oint_{S} \textbf{J} \cdot \textbf{dS}} = \frac{\int_{L} \textbf{E} \cdot \textbf{dl}}{\oint_{S} \sigma \textbf{E} \cdot \textbf{dS}} \label{eq2} \]

donde S es una superficie que rodea completamente un electrodo y L es cualquier camino que une los dos electrodos. Tenga en cuenta que la integral de línea de campo se toma a lo largo de la línea desde el electrodo de alto a bajo potencial para que la diferencia de voltaje V sea igual a la integral de línea positiva. De la Ecuación\ ref {eq2}, vemos que la resistencia solo depende de la geometría y conductividad\(\sigma\), y no de la magnitud del campo eléctrico en sí. Si aumentáramos el voltaje por cualquier factor, el campo también aumentaría en este mismo factor en todas partes para que este factor se cancelara en la relación de Ecuación\ ref {eq2}. La conductividad\(\sigma\) puede ser en sí misma una función de la posición.

Resistencia de placa paralela

Dos electrodos de placa paralelos perfectamente conductores de área A de forma arbitraria y espaciado l encierran un cilindro de material con conductividad óhmica\(\sigma\), como en la Figura 3-16 a. La corriente debe fluir tangencial a la superficie exterior ya que el medio exterior que es espacio libre tiene conductividad cero para que ninguna corriente pueda pasar a través de la interfaz. Debido a que el componente tangencial del campo eléctrico es continuo, existe un campo en la región de espacio libre que disminuye al aumentar la distancia desde la resistencia. Este campo tridimensional es difícil de calcular porque depende de tres coordenadas.

Figura 3-16 Geometrías simples de electrodos de resistencia. a) Placas paralelas. b) Cilindros coaxiales. c) Esferas concéntricas.

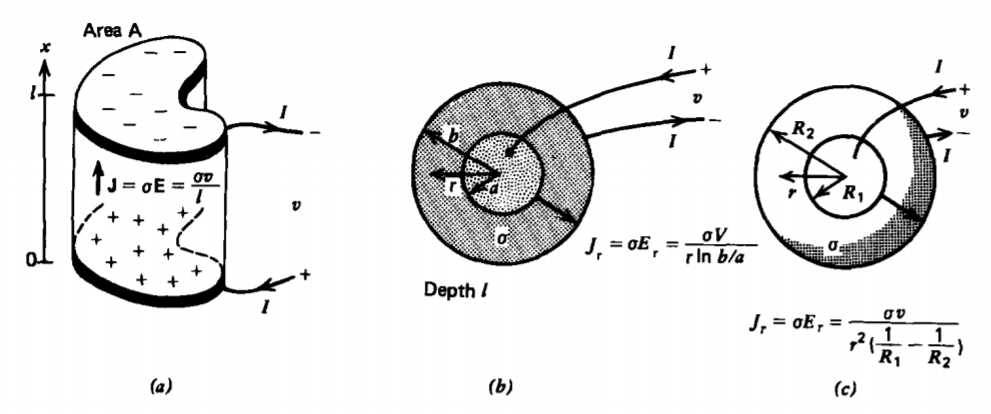
El campo eléctrico dentro de la resistencia es mucho más sencillo de calcular porque es perpendicular a los electrodos en la dirección x. La ley de Gauss sin carga de volumen nos dice entonces que este campo es constante:

\[\nabla \cdot (\varepsilon \textbf{E}) = 0 \Rightarrow \frac{dE_{x}}{dx} = 0 \Rightarrow E_{x} = E_{0} \nonumber \]

Sin embargo, la línea integral de E entre los electrodos debe ser la tensión aplicada\(v\):

\[\int_{0}^{l} E_{x} dx = v \Rightarrow E_{0} = v/l \nonumber \]

La densidad de corriente es entonces

\[\textbf{J} = \sigma E_{0} \textbf{i}_{x} = (\sigma v/l) \textbf{i}_{x} \nonumber \]

para que la corriente total a través de los electrodos sea

\[I = \oint_{S} \textbf{J} \cdot \textbf{dS} = (\sigma v/l)A \nonumber \]

donde la integral superficial se reduce a un producto puro debido a que la densidad de corriente constante incide perpendicularmente sobre los electrodos. La resistencia es entonces

\[\textrm{R} = \frac{v}{I} = \frac{l}{\sigma A} = \frac{\textrm{spacing}}{\textrm{(conductivity)(electrode area)}} \nonumber \]

Los valores típicos de resistencia pueden variar en muchos órdenes de magnitud. Si los electrodos tienen un área A = 1 cm ² (10 ^-4 m ²) con espaciamiento l = 1 mm (10 ^-3 m) un material como el cobre tiene una resistencia\(R \approx 0.17 \times 10^{-6}\) ohm mientras que el carbono tendría una resistencia\(R \approx 1.4 \times 10^{4}\) ohm. Debido a este amplio rango de valores de resistencia, las subunidades utilizadas a menudo son micro-ohmios (\(1 \mu \Omega = 10^{-6} \Omega\)), miliohmios (\(1 \textrm{ m} \Omega = 10^{-3} \Omega\)), kilohmios (\(1 \: k \Omega = 10^{3} \Omega\)) y megohmios (\(1 \textrm{ M} \Omega =10^{6} \Omega\)), donde el símbolo\(\Omega\) se usa para representar la unidad de ohmios.

Aunque el campo fuera de la resistencia es difícil de encontrar, sí sabemos que para distancias alejadas de la resistencia el campo se acerca al de un dipolo puntual debido a los electrodos de carga opuesta con densidad de carga

\[\sigma_{f}(x = 0) = - \sigma_{f}(x = l) = \varepsilon E_{0} = \varepsilon v/l \nonumber \]

y así momento dipolo

\[\textbf{p} = - \sigma_{f}(x =0) A l \textbf{i}_{x} = - \varepsilon A v \textbf{i}_{x} \nonumber \]

El signo menos surge porque el momento dipolo apunta de carga negativa a positiva. Tenga en cuenta que (8) solo es aproximado porque todas las líneas de campo externas en la región de espacio libre deben terminar en el lado y la parte posterior de los electrodos dando contribuciones adicionales a la densidad de carga superficial. Generalmente, si el espaciamiento de electrodos I es mucho menor que cualquiera de las dimensiones del electrodo, esta contribución extra es muy pequeña.

Resistor coaxial

Dos cilindros coaxiales perfectamente conductores de longitud l, radio interior a y radio exterior b se mantienen a una diferencia de potencial v y encierran un material con conductividad óhmica\(\sigma\), como en la Figura 3-16b. El campo eléctrico debe entonces ser perpendicular a los electrodos para que sin cargo libre la ley de Gauss requiera

\[\nabla \cdot (\varepsilon \textbf{E}) = 0 \Rightarrow \frac{1}{\textrm{r}} \frac{\partial}{\partial \textrm{r}} (\textrm{r} E_{\textrm{r}}) = 0 \Rightarrow E_{\textrm{r}} = \frac{c}{\textrm{r}} \nonumber \]

donde c es una constante de integración encontrada a partir de la condición de voltaje

\[\int_{a}^{b} E_{\textrm{r}} d \textrm{r} = c \ln \textrm{r} \big|_{a}^{b} = v \Rightarrow c = \frac{v}{\ln (b/a)} \nonumber \]

La densidad de corriente es entonces

\[\textbf{J}_{\textrm{r}} = \sigma E_{\textrm{r}} = \frac{\sigma v}{\textrm{r} \ln (b/a)} \nonumber \]

siendo la corriente total en cualquier radio r una constante

\[I = \int_{z=0}^{l} \int_{\phi=0}^{2\pi} J_{\textrm{r}} \textrm{r} d \phi dz = \frac{\sigma v 2 \pi l}{\ln(b/a)} \nonumber \]

para que la resistencia sea

\[\textrm{R} = \frac{v}{I} = \frac{\ln (b/a)}{2 \pi \sigma l} \nonumber \]

Resistor Esférico

Se procede de la misma manera para dos esferas concéntricas perfectamente conductoras a una diferencia de potencial\(v\) con el radio interior\(R_1\) y el radio exterior\(R_2\), como en la Figura 3-16 c. Sin carga gratuita, la simetría requiere que el campo eléctrico sea puramente radial para que la ley de Gauss rinda

\[\nabla \cdot (\varepsilon \textbf{E}) = 0 \Rightarrow \frac{1}{r^{2}} \frac{\partial}{\partial r}(r^{2}E_{r}) = 0 \Rightarrow E_{r} = \frac{c}{r^{2}} \nonumber \]

donde c es una constante encontrada a partir de la condición de voltaje como

\[\int_{R_{1}}^{R_{2}} E_{r}dr = - \frac{c}{r} \big|_{R_{1}}^{R_{2}} = v \Rightarrow c = \frac{v}{(1/R_{1}-1/R_{2})} \nonumber \]

El campo eléctrico y la densidad de corriente son inversamente proporcionales al cuadrado del radio

\[J_{r} = \sigma E_{r} = \frac{\sigma v}{r^{2}(1/R_{1} - 1/R_{2})} \nonumber \]

para que la densidad de corriente sea constante en cualquier radio\(r\)

\[I = \int_{\phi = 0}^{2 \pi} \int_{\theta =0}^{\pi} J_{r}r^{2} \sin \theta d \theta d \phi = \frac{4 \pi \sigma v}{(1/R_{1} - 1/R_{2})} \nonumber \]

con resistencia

\[\textrm{R} = \frac{v}{I} = \frac{(1/R_{1}-1/R_{2})}{4 \pi \sigma} \nonumber \]