3.5: Capacitancia

Electrodos de placa paralela

Electrodos de placa paralela de tamaño finito restringidos a diferencia de potencial v encierran un medio dieléctrico con permitividad\(\varepsilon\). La densidad de carga superficial no se distribuye uniformemente, como lo ilustran las líneas de campo de franjas para electrodos de placa paralela infinitamente delgados en la Figura 3-17 a. Cerca de los bordes el campo eléctrico es altamente no uniforme disminuyendo en magnitud en la parte posterior de los electrodos. Entre los electrodos, lejos de los bordes el campo eléctrico es uniforme, siendo el mismo que si los electrodos fueran infinitamente largos. Los efectos del campo de franjas pueden hacerse insignificantes si el espaciado de electrodos l es mucho menor que la profundidad d o el ancho w. Para un trabajo más preciso, los efectos finales se pueden hacer aún más insignificantes mediante el uso de un anillo de protección que rodea el electrodo superior, como en la Figura 3-17 b. El anillo protector se mantiene al mismo potencial que el electrodo, por lo tanto, a excepción del espacio muy pequeño, el campo entre

Figura 3-17 (a) Dos electrodos de placa paralela infinitamente delgados de área finita a diferencia de potencial v tienen campos altamente no uniformes fuera de la región interelectrodo. (b) Un anillo protector alrededor de un electrodo elimina los efectos finales para que el campo entre los electrodos sea uniforme. Los efectos finales ahora surgen en el borde del anillo de guardia, que está lejos de la región de interés.

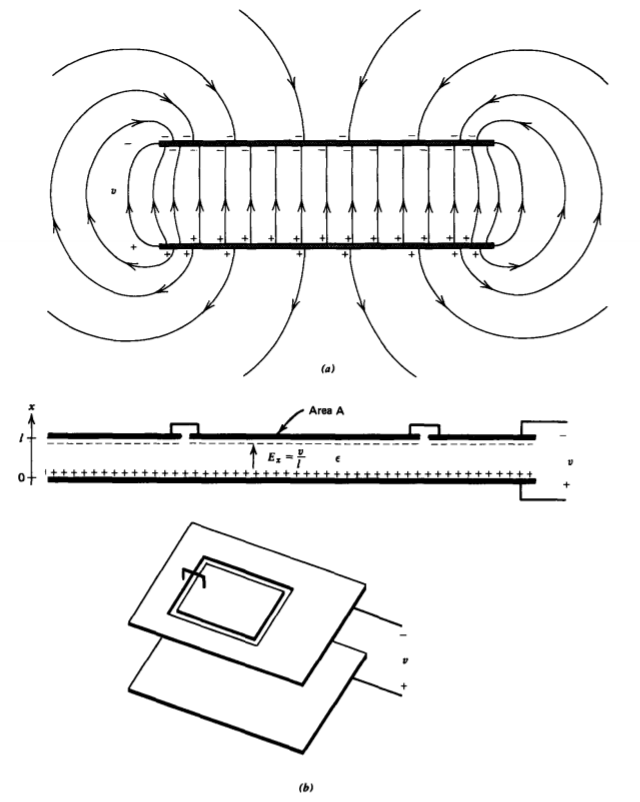
los electrodos es como si los efectos finales estuvieran muy lejos y no solo cerca de los bordes del electrodo.

A menudo usamos la frase “flecos de descuido” para significar que los efectos de campo no uniformes cerca de esquinas y bordes son insignificantes.

Con el descuido de los efectos de campo de flecos cerca de los extremos del electrodo, el campo eléctrico es perpendicular a los electrodos y relacionado con el voltaje como

\[\int_{0}^{l} E_{x}dx = v \Rightarrow E_{x} = v/l \nonumber \]

El vector de desplazamiento es entonces proporcional al campo eléctrico que termina en cada electrodo con una densidad de carga superficial de igual magnitud pero polaridad opuesta dada por

\[D_{x} = \varepsilon E_{x} = \sigma_{f}(x=0) = - \sigma_{F}(x = l) = \varepsilon v/l \nonumber \]

La carga es positiva donde la polaridad del voltaje es positiva, y viceversa, con el campo eléctrico dirigido del electrodo positivo al negativo. La magnitud de la carga libre total en cada electrodo es

\[q_{f} = \sigma_{f} (x = 0)A = \frac{\varepsilon A}{l} v \nonumber \]

La capacitancia C se define como la magnitud de la relación de carga libre total en cualquiera de los electrodos a la diferencia de voltaje entre electrodos:

\[C = \frac{q_{f}}{v} = \frac{\varepsilon A}{l} = \frac{\textrm{(permittivity)(electrode area)}}{\textrm{spacing}} \textrm{farad}[\textrm{A}^{2} \textrm{s}^{4} \textrm{kg}^{-1} \textrm{m}^{-2}] \nonumber \]

A pesar de que el sistema permanece neutro, los electrones móviles en el electrodo inferior son transportados a través de la fuente de voltaje al electrodo superior para terminar el campo de desplazamiento en las superficies del electrodo, manteniendo así los campos cero dentro de los conductores. Tenga en cuenta que no se transporta ningún cargo a través del espacio libre. El transporte de carga entre electrodos se debe al trabajo de la fuente de voltaje y da como resultado energía almacenada en el campo eléctrico.

En las unidades SI, los valores típicos de capacitancia son muy pequeños. Si los electrodos tienen un área de A = 1 cm ² (10 ^-4 m ²) con espaciamiento de l = 1 mm (10 ^-3 m), la capacitancia del espacio libre es\(C \approx 0.9 \times 10^{-12}\) farad. Por esta razón, los valores habituales de capacitancia se expresan en microfaradios (1\(\mu\) f = 10 ^-6 faradios), nanofaradios (1 nf = ^10-9 faradios) y picofaradios (1 pf = 10 ^-12 faradios).

Con un dieléctrico lineal de permitividad\(\varepsilon\) como en la Figura 3-18a, el campo de (1) permanece inalterado para un voltaje dado pero la carga en los electrodos y así la capacitancia aumenta con la permitividad, según lo dado por (3). Sin embargo, si la carga libre total en cada electrodo estuviera restringida, la diferencia de voltaje disminuiría por el mismo factor.

Estos resultados surgen debido a la presencia de cargas de polarización en los electrodos que cancelan parcialmente la carga libre. El vector de polarización dentro del condensador de placa paralela lleno de dieléctrico es una constante

\[P_{x} = D_{x} - \varepsilon_{0}E_{x} = (\varepsilon - \varepsilon_{0}) E_{x} = (\varepsilon - \varepsilon_{0}) v/l \nonumber \]

para que la densidad de carga de polarización de volumen sea cero. Sin embargo, con polarización cero en los electrodos, hay una discontinuidad en el componente normal de polarización en las superficies de los electrodos. La condición límite de la Sección 3.3.4 da como resultado una densidad de carga de polarización superficial de igual magnitud pero polaridad opuesta en cada electrodo, como se ilustra en

Figura 3-18 La presencia de un dieléctrico entre los electrodos aumenta la capacitancia debido a que para un voltaje dado se necesita carga libre adicional en cada electrodo para superar la neutralización parcial de los extremos dipolares de polaridad opuesta atraídos. (a) Electrodos de placa paralela. (b) Cilindros coaxiales. c) Esferas concéntricas.

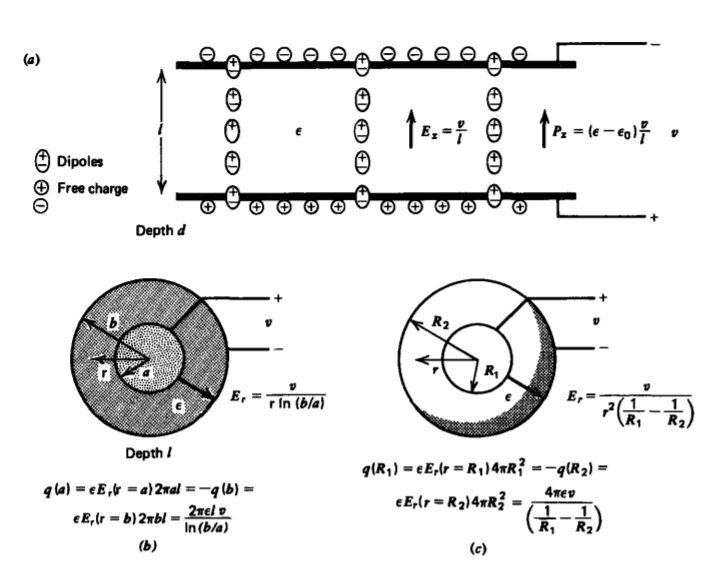
Figura 3-18a:

\[\sigma_{p} (x=0) = -\sigma_{p} (x=l) = - P_{x} = - (\varepsilon - \varepsilon_{0}) v/l \nonumber \]

Tenga en cuenta que la carga de polarización negativa aparece en el electrodo de polaridad positiva y viceversa. Esto se debe a que las cargas opuestas se atraen de manera que los extremos con carga opuesta de los dipolos se alinean a lo largo de la superficie del electrodo neutralizando parcialmente la carga libre.

Capacitancia 3-5-2 para cualquier geometría

Hemos basado nuestra discusión en torno a un condensador de placa paralela. Resultados similares se mantienen para electrodos de cualquier forma en un medio dieléctrico con la capacitancia definida como la magnitud de la relación de carga libre total en un electrodo a diferencia de potencial. La capacitancia es siempre positiva por definición y para los dieléctricos lineales es solo una función de la geometría y permitividad dieléctrica y no en los niveles de voltaje,

\[C = \frac{q_{f}}{v} = \frac{\oint_{S} \textbf{D} \cdot \textbf{dS}}{\int_{L} \textbf{E} \cdot \textbf{dl}} = \frac{\oint_{S} \varepsilon \textbf{E} \cdot \textbf{dS}}{\int_{L} \textbf{E} \cdot \textbf{dl}} \nonumber \]

ya que multiplicar el voltaje por un factor constante también aumenta el campo eléctrico por el mismo factor para que la relación permanezca sin cambios.

Las integrales en (7) son similares a las de la Sección 3.4.1 para un conductor óhmico. Para la misma geometría rellena con un conductor óhmico homogéneo o un dieléctrico lineal, el producto de resistencia-capacitancia es una constante independiente de la geometría:

\[\textrm{R} C = \frac{\int_{L} \textbf{E} \cdot \textbf{dl}}{\sigma \oint_{S} \textbf{E} \cdot \textbf{dS}} \frac{\varepsilon \oint_{S} \textbf{E} \cdot \textbf{dS}}{\int_{L} \textbf{E} \cdot \textbf{dl}} = \frac{\varepsilon}{\sigma} \nonumber \]

Así, para una geometría dada, si se conoce la resistencia o capacitancia, la otra cantidad se conoce inmediatamente a partir de (8). Así podemos anotar inmediatamente la capacitancia de las geometrías mostradas en la Figura 3-18 asumiendo que el medio entre electrodos es un dieléctrico lineal con permitividad e usando los resultados de las Secciones 3.4.2-3.4.4:

\[\textrm{Parallel Plate R} = \frac{l}{\sigma A} \Rightarrow C = \frac{\varepsilon A}{l} \\ \textrm{Coaxial R} = \frac{\ln (b/a)}{2 \pi \sigma l} \Rightarrow C = \frac{2 \pi \varepsilon l}{\ln (b/a)} \\ \textrm{Spherical R} = \frac{1/R_{1} - 1/R_{2}}{4 \pi \sigma} \Rightarrow C = \frac{4 \pi \varepsilon}{(1/R_{1} - 1/R_{2})} \nonumber \]

3-5-3 Flujo de corriente a través de un condensador

A partir de la definición de capacitancia en (7), la corriente a un electrodo es

\[i = \frac{dq_{f}}{dt} = \frac{d}{dt} (Cv) = C \frac{dv}{dt} + v \frac{dC}{dt} \nonumber \]

donde el último término solo surge si la geometría o permitividad dieléctrica cambia con el tiempo. Para la mayoría de las aplicaciones de circuitos, la capacitancia es independiente del tiempo y (10) se reduce a la relación habitual del circuito voltaje-corriente.

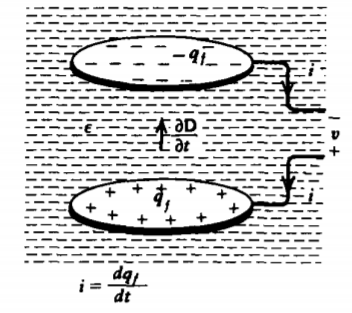
En el condensador de geometría arbitraria, mostrado en la Figura 3-19, una corriente de conducción i fluye a través de los cables hacia el electrodo superior y sale del electrodo inferior cambiando la cantidad de carga en cada electrodo, según lo dado por (10). No hay corriente de conducción que fluya en el dieléctrico entre los electrodos. Como se discute en la Sección 3.2.1 la corriente total, desplazamiento más conducción, es continua. Entre los electrodos en un condensador sin pérdidas, esta corriente es completamente corriente de desplazamiento. El campo de desplazamiento está en sí mismo relacionado con la distribución de carga superficial variable en el tiempo en cada electrodo, dada por la condición límite de la Sección 3.3.2.

Capacitancia 3-5-4 de dos esferas de contacto

Si el radio exterior _R2 del condensador esférico en (9) se pone en infinito, tenemos la capacitancia de una esfera aislada de radio R como

\[C = 4 \pi \varepsilon R \nonumber \]

Figura 3-19 La corriente de conducción i que viaja a través del cable de conexión a un electrodo en un condensador sin pérdidas se transmite a través del medio dieléctrico al electrodo opuesto a través de la corriente de desplazamiento. Los portadores sin carga viajan a través del dieléctrico sin pérdidas.

Si el medio circundante es espacio libre (\(\varepsilon = \varepsilon_{0}\)) para R = 1 m, tenemos ese\(C \approx \frac{1}{9} \times 10^{-9}\) farad\(\approx\) 111 pf.

Deseamos encontrar la autocapacitancia de dos esferas de contacto de este tipo elevadas a un potencial V _o, como se muestra en la Figura 3-20. La capacitancia se encuentra encontrando primero la carga total en las dos esferas. Podemos utilizar el método de imágenes colocando primero una carga de imagen\(q_{1} = Q = 4 \pi \varepsilon R V_{0}\) en el centro de cada esfera para llevar cada superficie al potencial V _o. No obstante, cada una de estas cargas inducirá una carga de imagen q ₂ en la otra esfera a una distancia b ₂ del centro,

\[q_{2} = - \frac{Q}{2}, \: \: \: \: b_{2} = \frac{R^{2}}{D} = \frac{R}{2} \nonumber \]

donde nos damos cuenta de que la distancia desde la inducción de carga hasta el centro de la esfera opuesta es D = 2 R. Esta carga de imagen no eleva el potencial de ninguna de las esferas. De igual manera, cada una de estas cargas de imagen induce otra carga de imagen q ₃ en la otra esfera a la distancia b ₃

\[Q_{3} = - \frac{q_{2}R}{D-b_{2}} = \frac{Q}{3}, \: \: \: \: b_{3} = \frac{R^{2}}{D-b_{2}} = \frac{2}{3}R \nonumber \]

lo que inducirá una carga de imagen adicional q ₄, ad infinitum. Será necesario un número infinito de cargas de imagen, pero con el uso de ecuaciones de diferencia podremos sumar todas las cargas de imagen para encontrar la carga total y así la capacitancia.

La n-ésima carga de imagen q _n y su distancia desde el centro b _n están relacionadas con las imágenes (n - 1) ésima como

\[q_{n} = - \frac{q_{n-1}R}{D-b_{n-1}}, \: \: \: \: b_{n} = \frac{R^{2}}{D-b_{n-1}} \nonumber \]

Figura 3-20 Dos esferas de contacto idénticas elevadas a un potencial V _O con respecto al infinito se describen cada una por un número infinito de cargas de imagen q _n cada una a una distancia _bn del centro de la esfera.

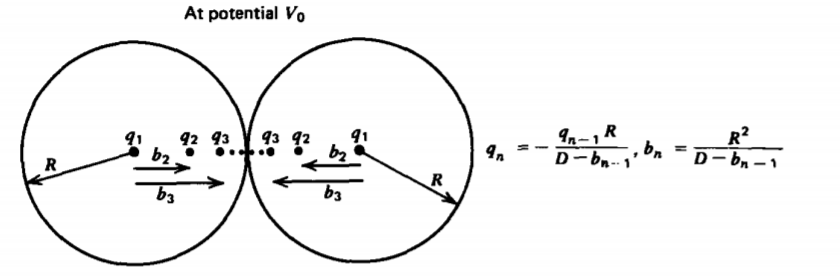
donde D = 2 R. Resolvemos la primera relación para b _{n -1} como

\[D - b_{n-1} = - \frac{q_{n-1}}{q_{n}} R \\ b_{n} = \frac{q_{n}}{q_{n+1}} R + D \nonumber \]

donde la segunda relación se encuentra incrementando n en la primera relación en 1. Sustituir (15) en la segunda relación de (14) nos da una sola ecuación en las q _n:

\[\frac{q_{n}R}{q_{n+1}} + D = - \frac{Rq_{n}}{q_{n-1}} \Rightarrow \frac{1}{q_{n+1}} + \frac{2}{q_{n}} + \frac{1}{q_{n-1}} = 0 \nonumber \]

Si definimos los cargos recíprocos como

\[p_{n} = 1/q_{n} \nonumber \]

entonces (16) se convierte en una ecuación de diferencia de coeficiente constante lineal homogénea

\[p_{n+1} + 2 p_{n} + p_{n-1} = 0 \nonumber \]

Así como las ecuaciones diferenciales de coeficiente constante lineal tienen soluciones exponenciales, (18) tiene soluciones de ley de poder de la forma

\[p_{n} = A \lambda^{n} \nonumber \]

donde las raíces características\(\lambda\), análogas a las frecuencias características, se encuentran por sustitución de nuevo en (18),

\[\lambda^{n+1} + 2 \lambda^{n} + \lambda^{n-1} = 0 \Rightarrow \lambda^{2} + 2 \lambda + 1 = (\lambda + 1)^{2} = 0 \nonumber \]

para producir una raíz doble con\(\lambda\) = -1. Debido a la doble raíz, la superposición de ambas soluciones es de la forma

\[p_{n} = A_{1}(-1)^{n} + A_{2}n(-1)^{n} \nonumber \]

similar al comportamiento encontrado en ecuaciones diferenciales con frecuencias de doble característica. La exactitud de (21) se puede verificar mediante la sustitución directa de nuevo en (18). Las constantes _{A1 y A2} se determinan a partir de q ₁ y q ₂ como

\[\left. \begin{matrix} P_{1} = 1/Q = -A_{1} -A_{2} \\ p_{2} = \frac{1}{q_{2}} = - \frac{2}{Q} = + A_{1} + 2A_{2} \end{matrix} \right \} \Rightarrow \left \{ \begin{matrix} A_{1} = 0 \\ A_{2} = - \frac{1}{Q} \end{matrix} \right. \nonumber \]

para que el cargo de la imagen n º sea

\[q_{n} = \frac{1}{p_{n}} = \frac{1}{-(-1)^{n} n/Q} = \frac{-(-1)^{n}Q}{n} \nonumber \]

La capacitancia se da entonces como la relación entre la carga total en las dos esferas y la tensión,

\[C = \frac{2 \sum_{n=0}^{\infty} q_{n}}{V_{0}} = - \frac{2Q}{V_{0}} \sum_{n=1}^{\infty} \frac{(-1)^{n}}{n} = + \frac{2Q}{V_{0}}[1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + ...\\ = 8 \pi \varepsilon R \ln 2 \nonumber \]

donde reconocemos que la serie infinita es la expansión de la serie Taylor de ln (1 + x) con x = 1. La capacitancia de dos esferas de contacto es así\(2 \ln 2 \approx 1.39\) multiplicada por la capacitancia de una sola esfera dada por (11).

La distancia desde el centro a cada carga de imagen se obtiene de (23) sustituido en (15) como

\[b_{n} = (\frac{(-1)^{n} (n + 1)}{n (-1)^{n+1}} + 2 ) R = \frac{(n-1)}{n}R \nonumber \]

Encontramos la fuerza de atracción entre las esferas tomando la suma de las fuerzas en cada carga de imagen en una de las esferas debido a todas las cargas de imagen en la otra esfera. La fuerza sobre la carga de imagen n ésima en una esfera debido a la carga de imagen m ésima en la otra esfera es

\[f_{nm} = \frac{-q_{n}q_{m}}{4 \pi \varepsilon [2R - b_{n} - b_{m}]^{2}} = \frac{-Q^{2}_{0}(-1)^{n+m}}{4 \pi \varepsilon R^{2}} \frac{nm}{(m + n)^{2}} \nonumber \]

donde usamos (23) y (25). La fuerza total en la esfera izquierda se encuentra entonces sumando sobre todos los valores de m y n,

\[f = \sum_{m=1}^{\infty} \sum_{n=1}^{\infty} f_{nm} = \frac{-Q_{0}^{2}}{4 \pi \varepsilon R^{2}} \sum_{m=1}^{\infty} \sum_{n=1}^{\infty} \frac{(-1)^{n+m}nm}{(n+m)^{2}} \\ = \frac{-Q_{0}^{2}}{4 \pi \varepsilon R^{2}} \frac{1}{6} [\ln 2 - \frac{1}{4}] \nonumber \]

donde se puede expresar explícitamente la serie doble.* La fuerza es negativa porque las esferas de carga similares se repelen entre sí. Si Q _o = 1 coul con R = 1 m, en el espacio libre esta fuerza es\(f \approx 6.6 \times 10^{8}\) nt, que puede levantar una masa en el campo de gravedad de la tierra de 6.8 x 10 ⁷ kg (\(\approx \times 10^{7}\)lb).

* Véase Albert D. Wheelon, Tablas de Series Sumables e Integrales que involucran funciones de Bessel, Holden Day, (1968) pp. 55, 56.