3.6: Medios con pérdida

Muchos materiales se describen tanto por una permitividad\(\varepsilon\) constante como por una conductividad óhmica constante\(\sigma\). Cuando tal material se coloca entre electrodos ¿tenemos un condensador o una resistencia? Escribimos las ecuaciones gobernantes de la conservación de cargas y la ley de Gauss con leyes constitutivas lineales:

\[\nabla \cdot \textbf{J}_{f} + \frac{\partial \rho_{f}}{\partial t} = 0, \: \: \: \textbf{J}_{f} = \sigma \textbf{E} + \rho_{f} \textbf{U} \nonumber \]

\[\nabla \cdot \textbf{D} = \rho_{f}, \: \: \: \textbf{D} = \varepsilon \textbf{E} \nonumber \]

Hemos generalizado la ley de Ohm en (1) para incluir corrientes de convección si el material se mueve con velocidad U. Además de los cargos de conducción, cualquier cargo libre que viaje con el material también contribuye a la corriente. El uso de (2) en (1) produce una única ecuación diferencial parcial en\(\rho_{f}\):

\[\sigma \underbrace{(\nabla \cdot \textbf{E})}{\rho_{f}/\varepsilon} + \nabla \cdot (\rho_{f} \textbf{U}) + \frac{\partial \rho_{f}}{\partial t} = 0 \Rightarrow \frac{\partial \rho_{f}}{\partial t} + \nabla \cdot (\rho_{f} \textbf{U}) + \frac{\sigma}{\varepsilon} \rho_{f} = 0 \nonumber \]

3-6-1 Relajación de carga transitoria

Supongamos primero que el medio es estacionario de manera que U =0. Entonces, la solución a (3) para cualquier distribución de carga inicial posiblemente variable espacialmente\(\rho_{0}(x, y, z, t = 0\) es

\[\rho_{f} = \rho_{0} (x, y, z, y = 0) e^{-t/\tau}, \: \: \tau = \varepsilon/ \sigma \nonumber \]

donde\(\tau\) está el tiempo de relajación. Esta solución es la versión continua del tiempo de decaimiento de resistencia-capacitancia (RC) en los circuitos.

La solución de (4) nos dice que en todas las posiciones dentro de un conductor, cualquier densidad de carga inicial muere exponencialmente con el tiempo. No se extiende en el espacio. Esta es nuestra justificación de no considerar ningún cargo de volumen neto en la realización de medios. Si un sistema no tiene carga de volumen a t =0 (\(\rho_{0}=0\)), permanece sin cargar durante todo el tiempo posterior. La carga es transportada a través de la región por la corriente óhmica, pero la carga neta sigue siendo cero. Incluso si sucede que hay una distribución inicial de carga de volumen, por tiempos mucho más largos que el tiempo de relajación, la densidad de carga volumétrica se vuelve insignificante. En metales,\(\tau\) es del orden de 10 ^-19 seg, lo que es la justificación de suponer que los campos son cero dentro de un electrodo. A pesar de que su gran conductividad no es infinita, por tiempos más largos que el tiempo de relajación\(\tau\), las soluciones de campo son las mismas que si un conductor estuviera perfectamente conductor.

Queda la pregunta de dónde va la carga relajada. La respuesta es que es transportada por la corriente de conducción a superficies de discontinuidad donde la conductividad cambia abruptamente.

3-6-2 Esfera con carga uniforme

Una esfera de radio _R2 con permitividad constante\(\varepsilon\) y conductividad óhmica\(\sigma\) se carga uniformemente hasta el radio _R1 con densidad de carga\(\rho_{0}\) en el tiempo t = 0, como en la Figura 3-21. De R ₁ a R ₂ la esfera está inicialmente descargada para que permanezca sin carga para siempre. La esfera está rodeada de espacio libre con permitividad\(\varepsilon_{0}\) y conductividad cero.

Desde (4) podemos anotar inmediatamente la distribución de carga por volumen para todos los tiempos,

\[\rho_{f} = \left \{ \begin{matrix} \rho_{0} e^{-t/ \tau}, & r<R_{1} \\ 0, & r>R_{1} \end{matrix} \right. \nonumber \]

donde\(\tau = \varepsilon / \sigma\). La carga total en la esfera permanece constante\(Q = \frac{4}{3} \pi R_{1}^{e} \rho_{0}\), pero la carga de volumen es transportada por la corriente óhmica a la interfaz en\(r = R_{2}\) donde se convierte en una carga superficial. Encerrando el sistema por una superficie gaussiana con\(r > R_{2}\) muestra que el campo eléctrico externo es independiente del tiempo,

\[E_{r} = \frac{Q}{4 \pi \varepsilon_{0}r^{2}}, \: \: \: r > R_{2} \nonumber \]

Del mismo modo, aplicar superficies gaussianas para\(r < R_{1}\) y\(R_{1} < r < R_{2}\) rendimientos

\[E_{r} = \left \{ \begin{matrix} \frac{\rho_{0}re^{-t/\tau}}{3 \varepsilon} = \frac{Qr e ^{-t/\tau}}{4 \pi \varepsilon R_{1}^{3}}, & 0 < r < R_{1} \\ \frac{Q e ^{-t/\tau}}{4 \pi \varepsilon r^{2}}, & R_{1} < r < R_{2} \end{matrix} \right. \nonumber \]

Figura 3-21 Una distribución inicial de carga de volumen dentro de un conductor óhmico decae exponencialmente hacia cero con el tiempo de relajación\(\tau = \varepsilon/\sigma\) y aparece como una carga superficial en una interfaz de discontinuidad. Inicialmente, las regiones sin carga siempre están descargadas con la carga transportada por la corriente.

La densidad de carga superficial a r = _R2 se acumula exponencialmente con el tiempo:

\[\sigma_{f}(r = R_{2}) = \varepsilon_{0} E_{r}(r = R_{2+}) - \varepsilon E_{r}(r = R_{2-}) = \frac{Q}{4 \pi R_{2}^{2}}(1 - e^{-t/\tau}) \nonumber \]

La carga se transporta desde la región cargada (r < R ₁) a la superficie a r = _R2 a través de la corriente de conducción con la densidad de carga entre (R ₁ < r < R ₂ ) cero restante:

\[J_{c} = \sigma E_{r} = \left \{ \begin{matrix} \frac{\sigma Q r}{4 \pi \varepsilon R_{1}^{3}} e^{t/\tau}, & 0<r<R_{1} \\ \frac{\sigma Q e^{-t/\tau}}{4 \pi \varepsilon r^{2}}, & R_{1} < r <R_{2} \\ 0, & r >R_{2} \end{matrix} \right. \nonumber \]

Tenga en cuenta que la corriente total, conducción más desplazamiento, es cero en todas partes:

\[-J_{c} = J_{d} = \varepsilon \frac{\partial E_{r}}{\partial t} = \left \{ \begin{matrix} -\frac{Qr \sigma e^{-t/\tau}}{4 \pi \varepsilon R_{1}^{3}}, & 0<r<R_{1} & - \frac{\sigma Q e^{-t/\tau}}{4 \pi \varepsilon r^{2}}, & R_{1} < r < R_{2} \\ 0, & r>R_{2} \end{matrix} \right. \nonumber \]

Capacitor con pérdida de la serie 3-6-3

a) Transitorio de carga

Para ejemplificar la diferencia entre el comportamiento resistivo y capacitivo se examina el caso de dos materiales diferentes en serie estresados por una tensión escalonada primero encendida a t =0, como se muestra en la Figura 3-22 a. Dado que lleva tiempo cargar la interfaz, la carga superficial interfacial no puede cambiar instantáneamente a t = 0 para que permanezca cero a t = 0 ₊. Sin densidad de carga superficial, el campo de desplazamiento es continuo a través de la interfaz de modo que la solución a t = 0 ₊ es la misma que para dos condensadores en serie sin pérdidas independientes de las conductividades:

\[D_{x} = \varepsilon_{1}E_{1}=\varepsilon_{2}E_{2} \nonumber \]

La restricción de voltaje requiere que

\[\int_{0}^{a+b} E_{x}dx = E_{1}a + E_{2}b = V \nonumber \]

Figura 3-22 Dos materiales dieléctricos con pérdidas diferentes en serie entre electrodos de placa paralelos tienen permitividades y conductividades óhmicas que cambian abruptamente a través de la interfaz. (a) A t = 0 ₊, justo después de aplicar un voltaje de paso, la interfaz se descarga para que el campo de desplazamiento sea continuo con la solución igual que para dos dieléctricos sin pérdidas en serie. (b) Dado que la corriente es discontinua a través del límite entre los materiales, la interfaz se cargará. En el estado estacionario de cc la corriente es continua. (c) Cada región es equivalente a una resistencia y un condensador en paralelo.

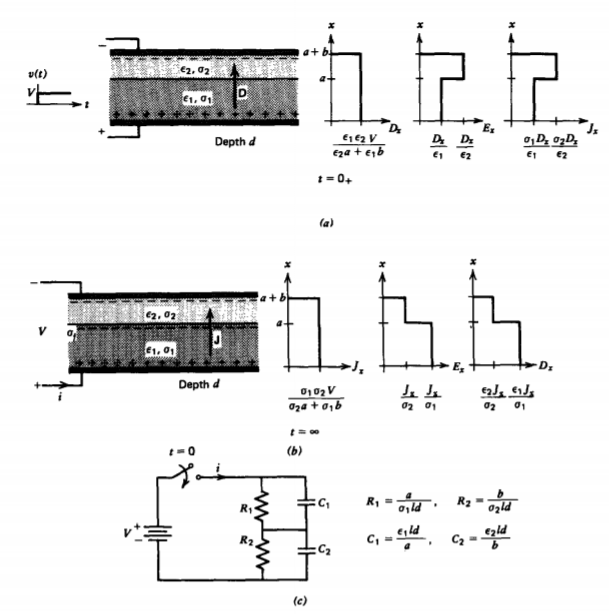
para que el campo de desplazamiento sea

\[D_{x}(t = 0_{+}) = \frac{\varepsilon_{1}\varepsilon_{2}V}{\varepsilon_{2}a + \varepsilon_{1}b} \nonumber \]

La corriente total de la batería se debe tanto a las corrientes de conducción como a las de desplazamiento. A t = 0, la corriente de desplazamiento es infinita (un impulso) ya que el campo de desplazamiento cambia instantáneamente de cero a (13) para producir la carga superficial en cada electrodo:

\[\sigma_{f}(x=0) = - \sigma_{f}(x = a + b) = D_{x} \nonumber \]

Después de que el voltaje ha estado encendido por mucho tiempo, los campos se acercan a sus valores de estado estacionario, como en la Figura 3-22b. Debido a que no hay más variaciones de tiempo, la densidad de corriente debe ser continua a través de la interfaz igual que para dos resistencias en serie independientes de las permitividades,

\[J_{x}(t \rightarrow \infty) = \sigma_{1}E_{1} = \sigma_{2}E_{2} = \frac{\sigma_{1}\sigma_{2}V}{\sigma_{2}a + \sigma_{1}b} \nonumber \]

donde nuevamente usamos (12). La carga superficial interfacial es ahora

\[\sigma_{f}(x=a) = \varepsilon_{2}E_{2} - \varepsilon_{1}E_{1} = \frac{(\varepsilon_{2} \sigma_{1} - \varepsilon_{1}\sigma_{2})V}{\sigma_{2}a + \sigma_{1}b} \nonumber \]

Lo que hemos demostrado es que para los primeros tiempos el sistema es puramente capacitivo, mientras que por largos tiempos el sistema es puramente resistivo. El intervalo transitorio intermedio se encuentra usando (12) con conservación de carga aplicada en la interfaz:

\[\textbf{n} \cdot (\textbf{J}_{2}-\textbf{J}_{1} + \frac{d}{dt}(\textbf{D}_{2} - \textbf{D}_{1})) = 0 \\ \Rightarrow \sigma_{2}E_{2}-\sigma_{1}E_{1} + \frac{d}{dt}[\varepsilon_{2}E_{2}-\varepsilon_{1}E_{1}]=0 \nonumber \]

Con (12) para relacionar E ₂ a E ₁ obtenemos una única ecuación diferencial ordinaria en E ₁,

\[\frac{dE_{1}}{dt} + \frac{E_{1}}{\tau} = \frac{\sigma_{2}V}{\varepsilon_{2}a + \varepsilon_{1}b} \nonumber \]

donde el tiempo de relajación es un promedio ponderado de los tiempos de relajación de cada material:

\[\tau = \frac{\varepsilon_{1}b + \varepsilon_{2}a}{\sigma_{1}b + \sigma_{2}a} \nonumber \]

Usando la condición inicial de (13) las soluciones para los campos son

\[E_{1} = \frac{\sigma_{2}V}{\sigma_{2}a + \sigma_{1}b}(1 - e^{-t/\tau}) + \frac{\varepsilon_{2}V}{\varepsilon_{2}a + \varepsilon_{1}b}e^{-t/\tau} \\ E_{2}= \frac{\sigma_{1}V}{\sigma_{2}a + \sigma_{1}b}(1 - e^{-t/\tau}) + \frac{\varepsilon_{1}V}{\varepsilon_{2}a + \varepsilon_{1}b}e^{-t/\tau} \nonumber \]

Señalar que a medida que\(t \rightarrow \infty\) las soluciones se acercan a las de (15). La carga superficial interfacial es

\[\sigma_{f}(x=a) = \varepsilon_{2}E_{2} - \varepsilon_{1} E_{1} = \frac{(\varepsilon_{2}\sigma_{1} - \varepsilon_{1}\sigma_{2})}{\sigma_{2}a + \sigma_{1}b}(1 - e^{-t/\tau})V \nonumber \]

que es cero a t = 0 y está de acuerdo con (16) para\(t \rightarrow \infty\).

La corriente total entregada por la fuente de voltaje es

\[i = (\sigma_{1}E_{1} + \varepsilon_{1}\frac{dE_{1}}{dt}) ld = (\sigma_{2}E_{2} + \varepsilon_{2} \frac{dE_{2}}{dt})ld \\ = [\frac{\sigma_{1}\sigma_{2}}{\sigma_{2}a + \sigma_{1}b} + (\sigma_{1} - \frac{\varepsilon_{1}}{\tau})(\frac{\varepsilon_{2}}{\varepsilon_{2}a + \varepsilon_{1}b} - \frac{\sigma_{2}}{\sigma_{2}a + \sigma_{1}b})e^{-t/\tau} \\ + \frac{\varepsilon_{1} \varepsilon_{2}}{\varepsilon_{2}a + \varepsilon_{1}b} \delta (t)] ldV \nonumber \]

donde el último término es la corriente de impulso que instantáneamente pone carga en cada electrodo en tiempo cero a t =0:

\[\delta(t) = \left \{ \begin{matrix} 0, \\ t \neq 0 \\ \infty, & t = 0 \end{matrix} \right \} \infty_{0_{-}}^{0_{+}} \delta (t) dt = 1 \nonumber \]

Para reiterar, vemos que para los primeros tiempos dominan las capacitancias y que en el estado estacionario las resistencias dominan con el tiempo de transición dependiendo de los tiempos de relajación y geometría de cada región. El circuito equivalente para el sistema se muestra en la Figura 3-22c como una combinación en serie de una resistencia-condensador paralelo para cada región.

(b) Circuito abierto

Una vez que el sistema está en el estado estacionario de CC, abrimos instantáneamente el circuito para que la corriente del terminal sea cero. Luego, usando (22) con i =0, vemos que los campos decaen independientemente en cada región con el tiempo de relajación de cada región:

\[E_{1} = \frac{\sigma_{2}V}{\sigma_{2}a + \sigma_{1}b} e^{-t/\tau_{1}}, \: \: \: \tau_{1} = \frac{\varepsilon_{1}}{\sigma_{1}} \\ E_{2} = \frac{\sigma_{1}V}{\sigma_{2}a + \sigma_{1}b}e^{-t/\tau_{2}}, \: \: \: \tau_{2} = \frac{\varepsilon_{2}}{\sigma_{2}} \nonumber \]

El voltaje de circuito abierto y la carga interfacial entonces decaen como

\[V_{\alpha} = E_{1}a + E_{2}b = \frac{V}{\sigma_{2}a + \sigma_{1}b} [\sigma_{2}a e^{-t/\tau_{1}} + \sigma_{1} b e^{-t/\tau_{2}} \\ \sigma_{f} = \varepsilon_{2}E_{2} - \varepsilon_{1}E_{1} = \frac{V}{\sigma_{2}a + \sigma_{1}b} [\varepsilon_{2} \sigma_{1} e^{-t/\tau_{2}} - \varepsilon_{1} \sigma_{2} e^{-t/\tau_{1}}] \nonumber \]

(c) Cortocircuito

Si el sistema de estado estacionario de CC está cortocircuitado, establecemos V = 0 en (12) y (18),

\[E_{1}a + E_{2}b = 0 \\ \frac{dE_{1}}{dt} + \frac{E_{1}}{\tau} = 0 \nonumber \]

donde todavía\(\tau\) está dado por (19). Dado que a t =0 la carga superficial interfacial no puede cambiar instantáneamente, los campos iniciales deben obedecer la relación

\[\lim_{t=0} (\varepsilon_{2}E_{2} - \varepsilon_{1}E_{1}) = - (\frac{\varepsilon_{2}a}{b} + \varepsilon_{1})E_{1} = \frac{(\varepsilon_{2} \sigma_{1} - \varepsilon_{1} \sigma_{2})V}{\sigma_{2}a + \sigma_{1}b} \nonumber \]

para producir las soluciones

\[E_{1} = - \frac{E_{2}b}{a} = - \frac{(\varepsilon_{2} \sigma_{1} - \varepsilon_{1} \sigma_{2})bV}{(\varepsilon_{2}a + \varepsilon_{1}b) (\sigma_{2}a + \sigma_{1}b)} e^{-t/\tau} \nonumber \]

La corriente de cortocircuito y la carga superficial son entonces

\[i = [(\frac{\sigma_{1}\varepsilon_{2} - \varepsilon_{1}\sigma_{2}}{\varepsilon_{1}b + \varepsilon_{2}a})^{2} \frac{abV}{(\sigma_{2}a + \sigma_{1}b)}e^{-t/\tau} - \frac{V \varepsilon_{1}\varepsilon_{2}}{\varepsilon_{2}a + \varepsilon_{1}b} \delta (t)] ld \\ \sigma_{f} = \varepsilon_{2}E_{2} - \varepsilon_{1}E_{1} = \frac{(\varepsilon_{2}\sigma_{1} - \varepsilon_{1} \sigma_{2})}{\sigma_{2}a + \sigma_{1} b} V e^{-t/\tau} \nonumber \]

El término de impulso en la corriente se debe al cambio instantáneo en el campo de desplazamiento de los valores de estado estacionario encontrados de (15) a los valores iniciales de (26).

d) Estado estacionario sinusoidal Ahora, en lugar de un voltaje escalonado, asumimos que el voltaje aplicado es sinusoidal,

\[v(t) = V_{0} \cos \omega t \nonumber \]

y ha estado en mucho tiempo. Los campos en cada región siguen siendo solo funciones de tiempo y no de posición. Es conveniente usar notación compleja para que todas las cantidades se escriban en la forma

\[v(t) = \textrm{Re} (V_{0}e^{j \omega t}) \\ E_{1}(t) = \textrm{Re} (\hat{E}_{1} e^{j \omega t}), \: \: \: \: E_{2}(t) = \textrm{Re}(\hat{E}_{2}e^{j \omega t}) \nonumber \]

Usando caretas por encima de un término para designar una amplitud compleja, la condición de voltaje aplicada de (12) requiere

\[\hat{E}_{1}a + \hat{E}_{2}b = V_{0} \nonumber \]

mientras que la ecuación de conservación de carga interfacial de (17) se convierte

\[\sigma_{2} \hat{E}_{2} - \sigma_{1} \hat{E}_{1} + j \omega (\varepsilon_{2}\hat{E}_{2} - \varepsilon_{1}\hat{E}_{1}) = [\sigma_{2} + j \omega \varepsilon_{2}]\hat{E}_{2} - [\sigma_{1} + j \omega \varepsilon_{1}] \hat{E}_{1} = 0 \nonumber \]

Las soluciones son

\[\frac{\hat{E}_{1}}{(j \omega \varepsilon_{2} + \sigma_{2})} = \frac{\hat{E}_{2}}{(j \omega \varepsilon_{1} + \sigma_{1})} = \frac{V_{0}}{[b(\sigma_{1} + j \omega \varepsilon_{1}) + a (\sigma_{2} + j \omega \varepsilon_{2})]} \nonumber \]

que da la amplitud de carga superficial interfacial como

\[\hat{\sigma}_{f} = \varepsilon_{2} \hat{E}_{2} - \varepsilon_{1}\hat{E}_{1} = \frac{(\varepsilon_{2}\sigma_{1} - \varepsilon_{1} \sigma_{2})V_{0}}{[b(\sigma_{1} + j \omega \varepsilon_{1}) + a(\sigma_{2} + j \omega \varepsilon_{2})] \nonumber \]

A medida que la frecuencia se vuelve mucho mayor que los tiempos de relajación recíproca,

\[\omega >> \frac{\sigma_{1}}{\varepsilon_{1}}, \: \: \: \omega >> \frac{\sigma_{2}}{\varepsilon_{2}} \nonumber \]

la densidad de carga superficial va a cero. Esto se debe a que la carga superficial no puede seguir el ritmo de las alternaciones de alta frecuencia y, por lo tanto, domina el componente capacitivo. Así, en el trabajo experimental se pueden prevenir acumulaciones de carga si las frecuencias de excitación son mucho más rápidas que los tiempos recíprocos de carga-relajación.

La corriente total a través de los electrodos es

\[\hat{I} = (\sigma_{1} + j \omega \varepsilon_{1}) \hat{E}_{1}ld = (\sigma_{2} + j \omega \varepsilon_{2}) \hat{E}_{2}ld \\ = \frac{ld(\sigma_{1} + j \omega \varepsilon_{1}) (\sigma_{2} + j \omega \varepsilon_{2}) V_{0}}{[b(\sigma_{1} + j \omega \varepsilon_{1}) + a(\sigma_{2} + j \omega \varepsilon_{2})]} \\ = \frac{V_{0}}{\frac{R_{2}}{R_{2}C_{2}j \omega + 1} + \frac{R_{1}}{R_{1}C_{1} j \omega + 1}} \nonumber \]

con el último resultado obtenido fácilmente del circuito equivalente en la Figura 3-22 c.

3-6-4 Sistemas Distribuidos

(a) Ecuaciones Gobernantes En todas nuestras discusiones hemos asumido que los electrodos son perfectamente conductores para que no tengan resistencia y el campo eléctrico termine perpendicularmente. Consideremos ahora la geometría de placa paralela mostrada en la Figura 3-23a, donde los electrodos tienen una conductividad grande pero finita\(\sigma_{c}\). Los electrodos ya no son superficies equipotenciales ya que a medida que la corriente pasa a lo largo del conductor se produce una caída de Ohmic i R.

Figura 3-23 Electrodos de placa paralela con pérdida con conductividad óhmica finita\(\sigma_{c}\), encierran un dieléctrico con pérdida con permitividad\(\varepsilon\) y conductividad\(\sigma\). (a) Este sistema puede ser modelado por una red distribuida de resistencia-condensador. (b) Las leyes de tensión y corriente de Kirchoff aplicadas a una sección de longitud\(\Delta z\) permiten describir el sistema mediante ecuaciones diferenciales parciales

La corriente también se deriva a través del dieléctrico con pérdidas para que fluya menos corriente en el extremo más alejado del conductor que cerca de la fuente. Podemos encontrar soluciones aproximadas dividiendo el sistema continuo en muchos pequeños segmentos de longitud\(\Delta z\). La resistencia del electrodo de esta pequeña sección es

\[\textrm{R} \Delta z = \frac{\Delta z}{\sigma_{c}ad} \nonumber \]

donde R =\(1/(\sigma_{c}ad)\) es solo la resistencia por unidad de longitud. Hemos mostrado en la sección anterior que el dieléctrico puede modelarse como una combinación de resistencia-condensador paralelo,

\[C \Delta z = \frac{\varepsilon d \Delta z}{s}, \: \: \frac{1}{G \Delta z} = \frac{s}{\sigma d \Delta z} \nonumber \]

C es la capacitancia por unidad de longitud y G es la conductancia por unidad de longitud donde la conductancia es la recíproca de la resistencia. Es más conveniente trabajar con la conductancia porque está en paralelo con la capacitancia.

Aplicamos las leyes de tensión y corriente de Kirchoff para la sección del circuito equivalente que se muestra en la Figura 3-23b:

\[v (z-\Delta z) - v(z) = 2 i (z) \textrm{R} \Delta z \\ i(z) - i(z + \Delta z) = C \Delta z \frac{dv(z)}{dt} + G \Delta zv (z) \nonumber \]

El factor de 2 en la ecuación superior surge de las resistencias en serie iguales de los conductores superior e inferior. Dividir por\(\Delta z\) y tomar el límite como\(\Delta z\) se vuelve infinitesimalmente pequeño produce las ecuaciones diferenciales parciales

\[- \frac{\partial v}{\partial z} = 2i \textrm{R} \\ - \frac{\partial i}{\partial z} = C \frac{\partial v}{\partial t} + Gv \nonumber \]

La toma\(\partial/ \partial z\) de la ecuación superior nos permite sustituir en la ecuación inferior para eliminar i,

\[\frac{\partial^{2}v}{\partial z^{2}} = 2 \textrm{R} C \frac{\partial v}{\partial t} + 2 \textrm{R} Gv \nonumber \]

que se denomina ecuación de difusión transitoria. Las ecuaciones (40) y (41) también son válidas para cualquier geometría cuyo área de sección transversal permanezca constante a lo largo de su longitud. El 2R representa la resistencia en serie por unidad de longitud de ambos electrodos, mientras que C y G son la capacitancia y conductancia por unidad de longitud del medio dieléctrico.

b) Estado estacionario

Si se aplica un voltaje de CC V _o, el voltaje de estado estacionario es

\[\frac{d^{2}v}{dz^{2}} - 2 \textrm{R} Gv = 0 \Rightarrow v = A_{1} \sinh \sqrt{2 \textrm{R} Gz} + A_{2} \cosh \sqrt{2 \textrm{R} Gz} \nonumber \]

donde las constantes se encuentran por las condiciones de contorno en z =0 y z = l,

\[v(z=0) = V_{0}, \: \: \: i(z=l) = 0 \nonumber \]

Tomamos el extremo z = l para estar en circuito abierto. Las soluciones son

\[v(z) = V_{0} \frac{\cosh \sqrt{2 \textrm{R}G}(z-l)}{\cosh \sqrt{2 \textrm{R} G} l} \\ i(z) = - \frac{1}{2 \textrm{R}} \frac{dv}{dz} = V_{0} \sqrt{\frac{G}{2 \textrm{R}}} \frac{\sinh \sqrt{2 \textrm{R}G}(z-l)}{\cosh \sqrt{2 \textrm{R} G}l} \nonumber \]

(c) Solución transitoria

Si este voltaje de CC se aplica como un paso a t = 0, el voltaje y la corriente tardan en llegar a estas distribuciones de estado estacionario. Debido a que (41) es lineal, podemos usar superposición y adivinar una solución para el voltaje que es la suma de la solución de estado estacionario en (44) y una solución transitoria que se apaga con el tiempo:

\[v(z,t) = \frac{V_{0} \cosh \sqrt{2 \textrm{R}G} (z-l)}{\cosh \sqrt{2 \textrm{R}G} l} + \hat{v}(z)e^{-\alpha t} \nonumber \]

En este punto no conocemos la función\(\hat{v}(z)\) o\(\alpha\). Sustituir la solución supuesta de (45) de nuevo en (41) produce la ecuación diferencial ordinaria

\[\frac{d^{2}\hat{v}}{dz^{2}} + p^{2}\hat{v} = 0, \: \: \: p^{2}=2 \textrm{R} C \alpha - 2 \textrm{R}G \nonumber \]

que cuenta con las soluciones trigonométricas

\[\hat{v}(z) = a_{1} \sin pz + a_{2} \cos pz \nonumber \]

Dado que la parte independiente del tiempo de (45) ya satisface las condiciones de contorno en z =0, la parte transitoria debe ser cero allí para que un ₂ =0. La contribución transitoria a la corriente i, encontrada de (40),

\[i(z,t) = V_{0} \sqrt{\frac{G}{2 \textrm{R}}} \frac{\sinh \sqrt{2 \textrm{R}G} (z-l)}{\cosh \sqrt{2 \textrm{R}G} l} + \hat{i}(z) e^{-\alpha t} \\ \hat{i}(z) = - \frac{1}{2 \textrm{R}} \frac{d \hat{v}(z)}{dz} = - \frac{pa_{1}}{2 \textrm{R}} \cos pz \nonumber \]

debe seguir siendo cero en z = l, lo que significa que pl debe ser un múltiplo entero impar de\(\pi\) /2,

\[pl = (2n + 1) \frac{\pi}{2} \Rightarrow \alpha_{n} = \frac{1}{2 \textrm{R} C} ((2n + 1) \frac{\pi}{2l})^{2} + \frac{G}{C}, \: \: \: \: \: n = 0,1,2... \nonumber \]

Dado que las condiciones de contorno permiten un número infinito de valores de\(\alpha\), la solución más general es la superposición de todas las soluciones permitidas:

\[v(z,t) = V_{0} \frac{\cosh \sqrt{2 \textrm{R}G}(z-l)}{\cosh \sqrt{2 \textrm{R}G} l} + \sum_{n=0}^{\infty} A_{n} \sin (2n + 1) \frac{\pi z}{2l} e^{-\alpha_{n}t} \nonumber \]

Esta solución satisface las condiciones límite pero no las condiciones iniciales a t = 0 cuando el voltaje se enciende por primera vez. Antes de aplicar la fuente de voltaje, la distribución de voltaje en todo el sistema es cero. Debe permanecer cero justo después de encenderse de lo contrario la derivada del tiempo en (40) sería infinita, lo que requiere corrientes infinitas no físicas. Así imponemos la condición inicial

\[v(z,t = 0) = 0 = V_{0} \frac{\cosh \sqrt{2 \textrm{R}G}(z-l)}{\cosh \sqrt{2 \textrm{R}G}l} + \sum_{n=0}^{\infty} A_{n} \sin (2n + 1) \frac{\pi z}{2l} \nonumber \]

Podemos resolver para las amplitudes A _n multiplicando (51) por pecado\((2m + 1) \pi z/2l\) y luego integrando sobre z de 0 a 1:

\[0 = \frac{V_{0}}{\cosh \sqrt{2 \textrm{R}G}l} \int_{0}^{l} \cosh \sqrt{2 \textrm{R} G} (z-l) \sin (2m + 1) \frac{\pi z}{2 l} dz \\ + \int_{0}^{l} \sum_{n=0}^{\infty} A_{n} \sin (2n + 1) \frac{\pi z}{2l} \sin (2m + 1) \frac{\pi z}{2l} dz \nonumber \]

El primer término se integra fácilmente escribiendo el coseno hiperbólico en términos de exponenciales, * mientras que el último término se integra a cero para todos los valores de m no iguales a n para que las amplitudes sean

\[A_{n} = - \frac{1}{l^{2}} \frac{\pi V_{0} (2n + 1)}{2 \textrm{R} G + [(2n + 1) \pi/2l]^{2}} \nonumber \]

Las soluciones totales son entonces

\[v(z,t) = \frac{V_{0} \cosh \sqrt{2 \textrm{R} G} (z-l)}{\cosh \sqrt{2 \textrm{R} G}l} \\ - \frac{\pi V_{0}}{l^{2}} \sum_{n=0}^{\infty} \frac{(2n + 1) \sin [(2n + 1)(\pi z/2l)]e^{\alpha_{n}t}}{2 \textrm{R} G + [(2n + 1) (\pi/2l)]^{2}} \\ i(z, t) = - \frac{1}{2 \textrm{R}} \frac{\partial v}{\partial z} \\ = - \frac{V_{0} \sqrt{G/2 \textrm{R}} \sinh \sqrt{2 \textrm{R}G}(z-l)}{ \cosh \sqrt{2 \textrm{R}G}l} \\ + \frac{\pi^{2} V_{0}}{4 l^{3} \textrm{R}} \sum_{n=0}^{\infty} \frac{(2n+1)^{2} \cos [(2n + 1) (\pi z/2l)]e^{-\alpha_{n}t}}{2 \textrm{R} G + [(2n + 1) ( \pi/2l)]^{2}} \nonumber \]

La constante de tiempo fundamental corresponde al valor más pequeño de\(\alpha\), que es cuando n = 0:

\[\tau_{0} = \frac{1}{\alpha_{0}} = \frac{C}{G + \frac{1}{2 \textrm{R}} (\frac{\pi}{2l})^{2}} \nonumber \]

Por tiempos largos en comparación con\(\tau_{0}\) el sistema se encuentra aproximadamente en estado estacionario. Debido a la rápida disminución exponencial por tiempos mayores a cero, la serie infinita en (54) a menudo se puede aproximar por el primer término. Estas soluciones se trazan en la Figura 3-24 para el caso especial donde G =0. Entonces la distribución de voltaje se acumula de cero a un valor constante que se difunde desde la izquierda. La corriente cercana a z =0 es inicialmente muy grande. A medida que aumenta el tiempo, con G =0, la corriente en todas partes disminuye hacia un estado estacionario cero.

*\(\int \cosh a(z-l) \sin bz \: dz \\ = \frac{1}{a^{2} + b^{2}} [a \sin \: bz \: \sinh \: a(z-l) - b \cos \: bh \cosh \: a(z-l)] \\ \int_{0}^{l} \sin (2n+1) bz \sin(2m+1) bz \: dz = \left \{ \begin{matrix} 0 & m \neq n \\ l/2 & m=n \end{matrix} \right.\)

3-6-5 Efectos de Convección

Hemos visto que en un medio estacionario cualquier densidad de carga inicial se descompone a una superficie de discontinuidad. Ahora deseamos centrar la atención en un sistema de estado estacionario de CC de un medio conductor que se mueve a velocidad constante U i _x, como en la Figura 3-25. Una fuente a x =0 mantiene una densidad de carga constante\(\rho_{0}\). Luego (3) en el estado estacionario de CC con constante

Figura 3-23a con G = 0 para una excitación de voltaje escalonado a z = 0 con el extremo z = l en circuito abierto. Los efectos de difusión surgen debido a los electrodos con pérdida donde se encuentra la constante de tiempo más larga\(\tau_{0} = 8 \textrm{R} Cl^{2}/\pi^{2}\).

Figura 3-25 Un material conductor en movimiento con velocidad U i _x tiende a tomar carga inyectada a x =0 con él. La densidad de carga en estado estacionario disminuye exponencialmente desde la fuente

la velocidad se convierte en

\[\frac{d \rho_{f}}{dx} + \frac{\sigma}{\varepsilon U} \rho_{f} = 0 \nonumber \]

que tiene soluciones en descomposición exponencial

\[\rho_{f} = \rho_{0} e^{-x/l_{m}}, \: \: \: \: l_{m} = \frac{\varepsilon U}{\sigma} \nonumber \]

donde l _m, representa una longitud de desintegración espacial característica. Si el sistema tiene área transversal A, la carga total q en el sistema es

\[q = \int_{0}^{\infty} \rho_{f}A \: dx = \rho_{0} l_{m}A \nonumber \]

3-6-6 La Tierra y su Atmósfera como Condensador Esférico con Fugantes*

En buen tiempo, en la superficie terrestre existe un campo eléctrico de CC con una fuerza aproximada de 100 V/m dirigido radialmente hacia el centro de la tierra. La magnitud del campo eléctrico disminuye con la altura sobre la superficie terrestre debido a la conductividad eléctrica no uniforme\(\sigma(r)\) de la atmósfera aproximada como

\[\sigma(r) = \sigma_{0} + a(r-R)^{2} \textrm{siemen/m} \nonumber \]

donde las mediciones han demostrado que y R ~6 x 106 metro es el radio de la tierra. La conductividad aumenta con la altura debido a la radiación cósmica en la atmósfera inferior. Debido a la radiación solar, la atmósfera actúa como un conductor perfecto por encima de los 50 km

\[\sigma_{0} \approx 3 \times 10^{-14} \\ a \approx .5 \times 10^{-20} \nonumber \]

En el estado estacionario de CC, la conservación de carga de la Sección 3-2-1 con simetría esférica requiere

\[\nabla \cdot \textbf{J} = \frac{1}{r^{2}} \frac{\partial}{\partial r} (r^{2}J_{r}) = 0 \Rightarrow J_{r} = \sigma(r)E_{r} = \frac{C}{r^{2}} \nonumber \]

donde se encuentra la constante de integración C especificando el campo eléctrico superficial\(E_{r} (R) \approx -100\) V/m

\[J_{r}(r) = \frac{\sigma(R)_{r}(R)R^{2}}{r^{2}} \nonumber \]

En la superficie terrestre la densidad de corriente es entonces

\[J_{r}(R) = \sigma(R) E_{r}(R) = \sigma_{0}E_{r}(R) \approx -3 \times 10^{-12} \textrm{amp/m{^{2} \nonumber \]

La corriente total dirigida radialmente hacia adentro sobre toda la tierra es entonces

\[I = \vert J_{r}(R) 4 \pi R^{2} \vert \approx 1350 \textrm{ amp} \nonumber \]

La distribución del campo eléctrico a través de la atmósfera se encuentra desde (62) como

\[E_{r}(R) = \frac{J_{r}(r)}{\sigma(r)} = \frac{\sigma(R)E_{r}(R)R^{2}}{r^{2}\sigma(r)} \nonumber \]

La densidad de carga superficial en la superficie terrestre es

\[\sigma_{f}(r=R) = \sigma_{0}E_{r}(R) \approx - 8.85 \times 10^{-10} \textrm{Coul/m}^{2} \nonumber \]

Esta distribución negativa de carga superficial (recuerde: E _{r (r}) < 0) se equilibra con una distribución positiva de carga volumétrica en toda la atmósfera

\[\rho_{f}(r) = \varepsilon_{0} \nabla \cdot \textbf{E} = \frac{\varepsilon_{0}}{r^{2}}\frac{\partial}{\partial r}(r^{2} E_{r}) = \frac{\varepsilon_{0} \sigma (R) E_{r}(R) R^{2}}{r^{2}} \frac{d}{dr} (\frac{1}{\sigma(r)}) \\ = \frac{- \varepsilon_{0} \sigma(R) E_{r}(R) R^{2}}{r^{2}(\sigma(r))^{2}}2a(r-R) \nonumber \]

La diferencia de potencial entre la atmósfera superior y la superficie terrestre es

\[V = - \int_{R}^{\infty} E_{r}(r)dr \\ = - \sigma (R)E_{r}(R)R^{2} \int_{R}^{\infty} \frac{dr}{r^{2}[\sigma_{0} + a(r-R)^{2}]} \\ = - \frac{\sigma(R)E_{r}(R)R^{2}}{a} \left \{ \begin{matrix} - \frac{R}{(R^{2} + \frac{\sigma_{0}}{a})^{2}} \ln \big[\frac{(r-R)^{2} + \frac{\sigma_{0}}{a}}{r^{2}}\big] - \frac{1}{r(R^{2} + \frac{\sigma_{0}}{a})} + \frac{(R^{2} - \frac{\sigma_{0}}{a})}{\sqrt{\frac{\sigma_{0}}{a}}(R^{2} + \frac{\sigma_{0}}{a})^{2}} \tan^{-1} \frac{(r-R)}{\sqrt{\frac{\sigma_{0}}{a}}} \end{matrix} \right \} \Bigg|_{r+R}^{\infty} \\ = - \frac{\sigma(R)E_{r}(R)}{a(R^{2} + \frac{\sigma_{0}}{a})^{2}}R^{2} \left \{ \begin{matrix} R \ln \frac{\sigma_{0}}{aR^{2}} + \frac{(R^{2} + \frac{\sigma_{0}}{a})}{R} + \frac{\frac{\pi}{2}(R^{2} - \frac{\sigma_{0}}{a})}{\sqrt{\frac{\sigma_{0}}{a}}} \end{matrix} \right \} \nonumber \]

Usando los parámetros de (60), vemos que de\(\sigma_{0}/a << R^{2}\) manera que (68) se reduce aproximadamente a

\[V \approx - \frac{\sigma_{0}E_{r}(R)}{aR^{2}} \left \{ \begin{matrix} R \big(\ln \frac{\sigma_{0}}{a R^{2}} + 1 \big) + \frac{\pi R^{2}}{2 \sqrt{\frac{\sigma_{0}}{a}}} \end{matrix} \right \} \\ \approx 384,000 \textrm{volts} \nonumber \]

Si no se reponía la carga terrestre, el flujo de corriente neutralizaría la carga en la superficie terrestre con una constante de tiempo de orden

\[\tau = \frac{\varepsilon_{0}}{\sigma_{0}} \approx 300 \textrm{ seconds} \nonumber \]

Se piensa que las regiones tormentosas localizadas activas simultáneamente en todo el mundo sirven como “baterías” para mantener la tierra cargada a través de relámpagos carizados negativamente a tierra y corona a nivel del suelo, produciendo carga que se mueve del suelo a la nube. Esta corriente de tormenta eléctrica debe ser ascendente y equilibra la corriente a la baja de clima justo de (64).

* M. A. Uman, “The EarthAndits Atmosphere asa Leaky Sphere Capacitor, "Am. J. Phys. V. 42, nov. 1974, pp. 1033-1035.