3.7: Distribuciones de carga espacial dependientes del campo

Un conductor óhmico estacionario con conductividad constante se mostró en la Sección 3-6-1 que no soporta una distribución de carga volumétrica en estado estacionario. Esto ocurre porque en nuestro.modelo óhmico clásico en la Sección 3-2-2c una especie de carga (e.g., electrones en metales) se mueve con relación a una especie de fondo estacionario de carga con polaridad opuesta para que se mantenga la neutralidad de carga. Sin embargo, si solo se inyecta una especie de carga en un medio, puede resultar una distribución neta de carga de volumen en estado estacionario.

Debido a la fuerza eléctrica, esta distribución de carga volumétrica\(\rho_{f}\) contribuye y también a su vez depende del campo eléctrico. Ahora se hace necesario satisfacer simultáneamente las ecuaciones eléctricas y mecánicas acopladas

3-7-1 Diodo de tubo de vacío limitado de carga espacial

En los diodos de tubo de vacío, los electrones con carga - e y masa m se hierven del cátodo calentado, que tomamos como nuestra referencia de potencial cero. Este proceso se llama emisión termiónica. Un potencial positivo V _o aplicado al ánodo a x = l acelera los electrones, como en la Figura 3-26.

Figura 3-26 Diodo de tubo de vacío limitado de carga espacial. (a) Inyección termiónica de electrones del cátodo calentado al vacío con velocidad inicial cero. El potencial anódico positivo atrae al electrón cuya aceleración es proporcional al campo eléctrico local. b) Distribución de potencial en estado estacionario, campo eléctrico y carga volumétrica.

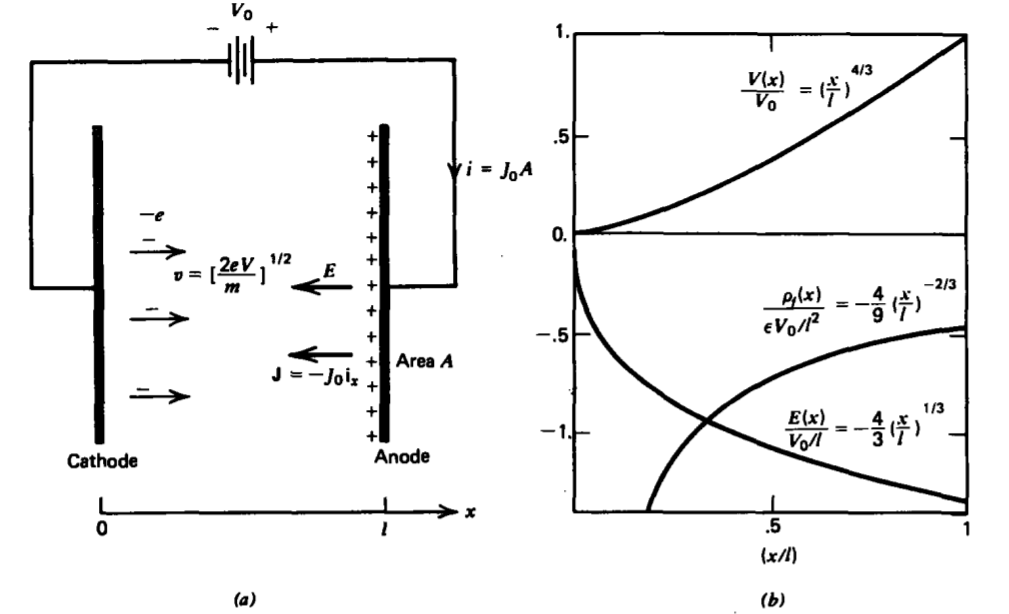
La ley de Newton para un electrón en particular es

\[m \frac{dv}{dt} = - eE = e \frac{dV}{dx} \nonumber \]

En el estado estacionario dc la velocidad del electrón depende únicamente de su posición x de manera que

\[m \frac{dv}{dt} = m \frac{dv}{dx} \frac{dx}{dt} = mv \frac{dv}{dx} \Rightarrow \frac{d}{dx}( \frac{1}{2} mv^{2}) = \frac{d}{dx}(eV) \nonumber \]

Con esta última igualdad, hemos derivado el teorema de conservación de energía

\[\frac{d}{dx}[\frac{1}{2}mv^{2} - eV] = 0 \Rightarrow \frac{1}{2} mv^{2} - eV = \textrm{const} \nonumber \]

donde decimos que la energía cinética\(\frac{1}{2}mv^{2}\) más la energía potencial - eV es la energía total constante. Nos limitamos aquí al caso más simple donde la carga inyectada en el cátodo comienza con velocidad cero. Dado que el potencial también se elige para que sea cero en el cátodo, la constante en (3) es cero. La velocidad se relaciona entonces con el potencial eléctrico como

\[v = (\frac{2e}{m}V)^{1/2} \nonumber \]

En el estado estacionario independiente del tiempo la densidad de corriente es constante,

\[\nabla \cdot \textbf{J} = 0 \Rightarrow \frac{dJ_{x}}{dx} = 0 \Rightarrow \textbf{J} = - J_{0} \textbf{i}_{x} \nonumber \]

y se relaciona con la densidad de carga y velocidad como

\[J_{0} = - \rho_{f}v \Rightarrow \rho_{f} = -J_{0}(\frac{m}{2e})^{1/2} V^{-1/2} \nonumber \]

Tenga en cuenta que la corriente fluye de ánodo a cátodo, y por lo tanto está en la dirección x negativa. Este signo menos se incorpora en (5) y (6) para que Jo sea positivo. La ecuación de Poisson entonces requiere que

\[\nabla^{2}V = \frac{-\rho_{f}}{\varepsilon} \Rightarrow \frac{d^{2}V}{dx^{2}} = \frac{J_{0}}{\varepsilon}(\frac{m}{2e})^{1/2}V^{-1/2} \nonumber \]

Las soluciones de ley de poder a esta ecuación diferencial no lineal se adivinan de la forma

\[V = Bx^{p} \nonumber \]

que cuando se sustituye en (7) rinde

\[Bp(p-1)x^{p-2} = \frac{J_{0}}{\varepsilon}(\frac{m}{2e})^{1/2}B^{-1/2} x^{-p/2} \nonumber \]

Para que esta supuesta solución se mantenga para todos x requerimos que

\[p-2 = -\frac{p}{2} \Rightarrow p = \frac{4}{3} \nonumber \]

que luego nos da la amplitud B como

\[B = \big[ \frac{9}{4} \frac{J_{0}}{\varepsilon} \big(\frac{m}{2e}\big)^{1/2} \big]^{2/3} \nonumber \]

para que el potencial sea

\[V(x) = \big[ \frac{9}{4} \frac{J_{0}}{\varepsilon} \big( \frac{m}{2e} \big)^{1/2}\big]^{2/3} x^{4/3} \nonumber \]

El potencial es cero en el cátodo, según sea necesario, mientras que el potencial anódico V o requiere que la densidad de corriente sea

\[V(x=l) = V_{0} = \big[\frac{9}{4} \frac{J_{0}}{\varepsilon} \big(\frac{m}{2e} \big)^{1/2} \big]^{2/3} l^{4/3} \\ \Rightarrow J_{0} \frac{4}{9} \frac{\varepsilon}{l^{2}} \big( \frac{2e}{m} \big) ^{1/2} V_{0}^{3/2} \nonumber \]

que se llama la ley Langmuir-Child.

El potencial, el campo eléctrico y las distribuciones de carga se escriben entonces de manera concisa como

\[V(x) = V_{0} \bigg( \frac{x}{l} \big)^{4/3} \\ E(x) = - \frac{dV(x)}{dx} = - \frac{4}{3} \frac{V_{0}}{l} \bigg( \frac{x}{l} \bigg)^{1/3} \\ \rho_{f}(x)= \varepsilon \frac{dE (x)}{dx} = - \frac{4}{9} \varepsilon \frac{V_{0}}{l^{2}} \bigg( \frac{x}{l} \bigg) ^{-2/3} \nonumber \]

y se representan en la Figura 3-26b. Vemos que la densidad de carga en el cátodo es infinita pero que la carga total entre los electrodos es finita,

\[q_{\tau} = \int_{x=0}^{l} \rho_{f}(x) A \: dx = - \frac{4}{3} \varepsilon \frac{V_{0}}{l}A \nonumber \]

siendo igual en magnitud pero opuesto en signo a la carga superficial total en el ánodo:

\[q_{A} = \sigma_{f}(x=l)A = - \varepsilon E (x=l) A = + \frac{4}{3} \varepsilon \frac{V_{0}}{l}A \nonumber \]

No hay carga superficial en el cátodo porque ahí el campo eléctrico es cero.

Este desplazamiento x de cada electrón se puede encontrar sustituyendo la distribución potencial de (14) en (4),

\[v = \frac{dx}{dt} = \bigg(\frac{2eV_{0}}{m} \bigg)^{1/2} \bigg( \frac{x}{l} \bigg)^{2/3} \Rightarrow \frac{dx}{x^{2/3}} = \bigg( \frac{2e V_{0}}{ml^{4/3}}\bigg)^{1/2} dt \nonumber \]

que se integra a

\[x = \frac{1}}{27} \bigg( \frac{2eV_{0}}{ml^{4/3}}\bigg)^{3/2}t^{3} \nonumber \]

El tiempo de tránsito de carga\(\tau\) entre electrodos se encuentra resolviendo (18) con x = l:

\[\tau = 3l\bigg(\frac{m}{2eV_{0}}\bigg)^{1/2} \nonumber \]

Para un electrón (\(m = 9.1 \times 10^{-31}\)kg,\(e = 1.6 \times 10^{-19}\) coul) con 100 voltios aplicados a través de l = 1cm (10 ^-2 m) este tiempo es\(\tau \approx 5 \times 10^{-9}\) seg. La velocidad máxima de los electrones cuando alcanza el ánodo es\(v (x=l) \approx 6 \times 10^{6}\) m/seg, que es aproximadamente 50 veces menor que la velocidad de vacío de la luz.

Debido a estos rápidos tiempos de respuesta, los diodos de tubo de vacío se utilizan en aplicaciones de voltaje alterno para rectificación ya que la corriente solo fluye cuando el ánodo es positivo y como elementos de circuito no lineales debido a la ley de potencia de tres mitades de (13) que relacionan corriente y voltaje.

3-7-2 Carga Espacial Conducción Limitada en Dieléctricos

Las propiedades de conducción de los dieléctricos a menudo se examinan inyectando carga. En la Figura 3-27, un haz de electrones con densidad\(\textbf{J} = - J_{0} \textbf{i}_{x}\) de corriente se enciende repentinamente a t = 0.* En medios, la aceleración de la carga ya no es proporcional al campo eléctrico. Más bien, las colisiones con el medio introducen un arrastre friccional de manera que la velocidad es proporcional al campo eléctrico a través de la movilidad de los electrones\(\mu\):

\[\textbf{V} = \mu \textbf{E} \nonumber \]

A medida que los electrones penetran en el dieléctrico, el frente de carga espacial está a una distancia s de la interfaz donde (20) nos da

\[ds/dt = - \mu E(s) \nonumber \]

Aunque la densidad de carga no se distribuye uniformemente detrás del frente de onda, la carga total Q dentro del dieléctrico detrás del frente de onda en el tiempo t está relacionada con la densidad de corriente como

\[J_{0}A = \rho_{f} \mu E_{x}A = -Q/t \Rightarrow Q = -J_{0}At \nonumber \]

La ley de Gauss aplicada a la superficie rectangular que encierra toda la carga dentro del dieléctrico luego relaciona los campos en la interfaz y el frente de carga a esta carga como

\[\oint_{S} \varepsilon \textbf{E} \cdot \textbf{dS} = [\varepsilon E (s) - \varepsilon_{0}\textbf{E}(0)]A = Q = -J_{0}At \nonumber \]

Figura 3-27 (a) Un haz de electrones que transporta una corriente\(-J_{0}\textbf{i}_{x}\) se enciende a t = 0. Los electrones viajan a través del dieléctrico con movilidad\(\mu\). (b) El frente de carga espacial, a una distancia s frente a la interfaz limitada de carga espacial en x =0, viaja hacia el electrodo opuesto. (c) Después del tiempo de tránsito\ (t_ {c} = [2\ varepsilon l/\ mu J_ {0}] ^ {1/2} las distribuciones de potencial de estado estacionario, campo eléctrico y carga espacial.

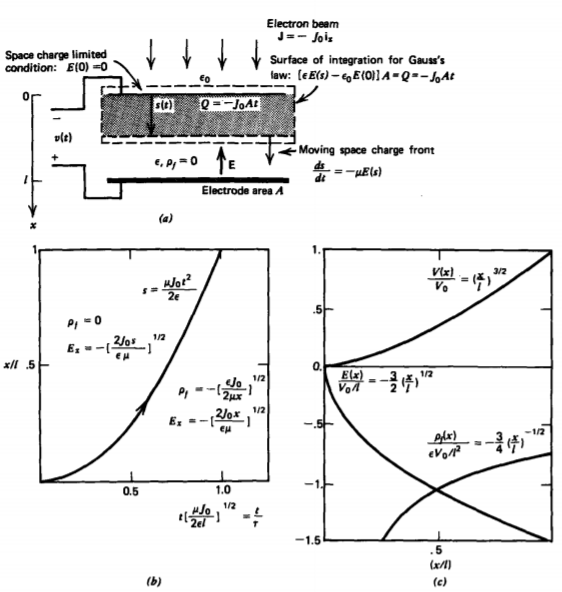
La corriente máxima fluye cuando E (0) =0, lo que se denomina conducción limitada de carga espacial. Entonces usar (23) en (21) nos da la dependencia temporal del frente de carga espacial:

\[\frac{ds}{dt} = \frac{\mu J_{0}t}{\varepsilon} \Rightarrow s(t) = \frac{\mu J_{0}t^{2}}{2 \varepsilon} \nonumber \]

Detrás del frente la ley de Gauss requiere

\[\frac{dE_{x}}{dx} = \frac{\rho_{f}}{\varepsilon} = \frac{J_{0}}{\varepsilon \mu E_{x}} \Rightarrow E_[x} \frac{dE_{x}}{dx} = \frac{J_{0}}{\varepsilon \mu} \nonumber \]

mientras que por delante de la carga del espacio móvil la densidad de carga es cero de manera que la corriente es transportada completamente por la corriente de desplazamiento y el campo eléctrico es constante en el espacio. La distribución espacial del campo eléctrico se obtiene entonces integrando (25) a

\[E_{x} = \left \{ \begin{matrix} - \sqrt{2J_{0}x/\varepsilon \mu,} & 0 \leq x \leq s(t) \\ - \sqrt{2 J_{0}s/\varepsilon \mu,} & s(t) \leq x \leq l \end{matrix} \right. \nonumber \]

mientras que la distribución de carga es

\[\rho_{f} = \varepsilon \frac{dE_{x}}{dx} = \left \{ \begin{matrix} - \sqrt{\varepsilon J_{0}/(2 \mu x), & 0 \leq x \leq s(t) \\ 0& s(t) \leq x \leq l \end{matrix} \right. \nonumber \]

como se indica en la Figura 3-27b.

La dependencia del tiempo del voltaje a través del dieléctrico es entonces

\[v(t) = \int_{0}^{t} E_{x}dx = \int_{0}^{s(t) \sqrt{\frac{2J_{0}x}{\varepsilon \mu}}dx + \int_{s(t)^{t} \sqrt{\frac{2J_{0}s}{\varepsilon \mu}}dx = \frac{J_{0}lt}{\varepsilon} - \frac{\mu J_{0}^{2}t^{3}}{6 \varepsilon^{2}}, \: \: \: s(t) \leq l \nonumber \]

Estas soluciones transitorias son válidas hasta que el frente de carga espacial s, dado por (24), alcanza el electrodo opuesto con s = l en el tiempo

\[\tau = \sqrt{2 \varepsilon l/ \mu J_{0}} \nonumber \]

A partir de entonces, el sistema está en el estado estacionario de CC con el voltaje terminal V _o relacionado con la densidad de corriente como

\[J_{0} = \frac{9}{8} \frac{\varepsilon \mu V_{0}^{2}}{l^{3}} \nonumber \]

que es la ley análoga de Langmuir-Child para los medios de comunicación dominados por colisiones. El campo eléctrico de estado estacionario y la densidad de carga espacial se escriben entonces de manera concisa como

\[E_{x} = - \frac{3}{2} \frac{V_{0}}{l} \bigg( \frac{x}{l} \bigg)^{1/2}, \: \: \: \rho_{f} = \varepsilon \frac{dE}{dx} = - \frac{3}{4} \frac{\varepsilon V_{0}}{l^{2}} \bigg( \frac{x}{l} \bigg)^{-1/2} \nonumber \]

y se representan en la Figura 3-27c.

En líquidos una movilidad iónica típica es del orden de 10 ^-7 m ²/(volt-seg) con una permitividad de\(\varepsilon = 2 \varepsilon_{0} \approx 1.77 \times 10^{-11}\) farad/m. para un espaciado de l =10 ^-2 m con una diferencia de potencial de\(V_{0}=10^{4}V\) la densidad de corriente de (30) es\(J_{0} \approx 2 \times 10^{-4}\) amp/m ² con el tiempo de tránsito dado por (29)\(\tau \approx 0.133\) sec. Los tiempos de transporte de carga en medios dominados por colison son mucho mayores que en el vacío.

* Véase P. K. Watson, J. M. Schneider, y H. R. Till, Estabilidad electrohidrodinámica de corrientes limitadas de carga espacial en líquidos dieléctricos. II. Estudio Experimental, Phys. Fluidos 13 (1970), p. 1955.