3.8: Energía almacenada en un medio dieléctrico
- Page ID
- 86761
El trabajo necesario para ensamblar una distribución de carga se almacena como energía potencial en el campo eléctrico ya que si se permite que las cargas se muevan este trabajo se puede recuperar como energía cinética o trabajo mecánico.
3-8-1 Trabajo necesario para ensamblar una distribución de cargas puntuales
a) Ensamblar los Cargos
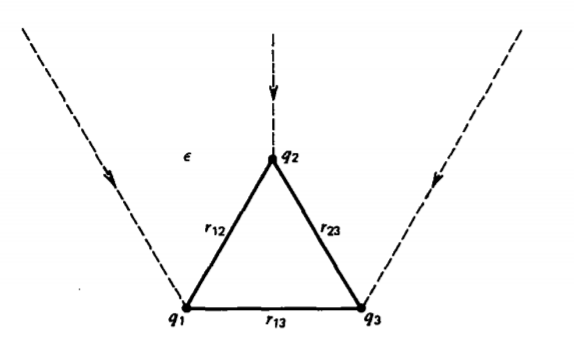
Calculemos el trabajo necesario para llevar tres libres ya existentes q 1, q 2, y q 3 desde el infinito hasta cualquier posición, como en la Figura 3-28. No se necesita trabajo para traer la primera carga ya que no hay campo eléctrico presente. El trabajo necesario para traer la segunda carga deberá superar el campo debido a la primera carga, mientras que el trabajo necesario para traer la tercera carga deberá superar los campos debido a ambos otros cargos. Dado que el potencial eléctrico desarrollado en la Sección 2-5-3 se define como el trabajo por unidad de carga necesaria para traer una carga puntual desde el infinito, el trabajo total necesario para traer las tres cargas es
\[W = q_{1}(0) + q_{2} \bigg( \frac{q_{1}}{4 \pi \varepsilon r_{12} \bigg) + q_{3} \bigg( \frac{q_{1}}{4 \pi \varepsilon r_{13}} + \frac{q_{2}}{4 \pi \varepsilon r_{23} \bigg) \nonumber \]
donde las distancias finales entre las cargas se definen en la Figura 3-28 y utilizamos la permitividad\(\varepsilon\) del medio. Podemos reescribir (1) en la forma más conveniente
\[W = \frac{1}{2} \left \{ \begin{matrix} q_{1} \bigg[ \frac{q_{2}}{4 \pi \varepsilon r_{12}} + \frac{q_{3}}{4 \pi \varepsilon r_{13}} \bigg] + q_{2} \bigg[\frac{q_{1}}{4 \pi \varepsilon r_{12}} + \frac{q_{3}}{4 \pi \varepsilon r_{23}} \bigg] + q-{3} \bigg[\frac{q_{1}}{4 \pi \varepsilon r_{13}} + \frac{q_{2}}{4 \pi \varepsilon r_{23}} \bigg] \end{matrix} \right \} \nonumber \]
donde reconocemos que cada término entre corchetes es solo el potencial en la posición final de cada cargo e incluye contribuciones de todos los demás cargos, excepto el que se encuentra en la posición donde se está evaluando el potencial:
\[W = \frac{1}{2} [q_{1} V_{1} + q_{2}V_{2} + q_{3}V_{3} \nonumber \]
Ampliar este resultado para cualquier número N de rendimiento de cargos por puntos libres ya existentes
\[W = \frac{1}{2} \sum_{n=1}^{N} q_{n}V_{n} \nonumber \]
El factor de\(\frac{1}{2}\) surge porque el potencial de una carga puntual en el momento en que se introduce desde el infinito es menor que el potencial final cuando se ensamblan todas las cargas.
(b) Energía de Unión de un Cristal
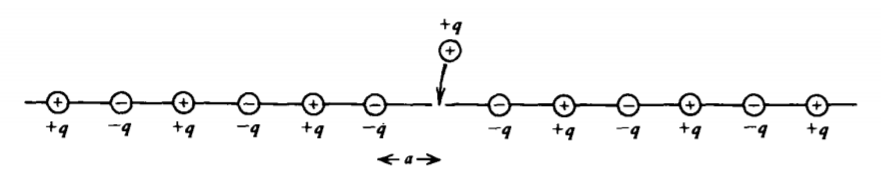
Una aplicación importante de (4) es en el cálculo de la mayor contribución a la energía de unión de los cristales iónicos, como la sal (NaCl), que se conoce como la energía electrostática de Madelung. Tomamos un simple modelo unidimensional de un cristal que consiste en una cadena infinitamente larga de cargas puntuales de polaridad alterna a\(\pm q\) una distancia a una distancia, como en la Figura 3-29. El trabajo promedio necesario para llevar una carga positiva como se muestra en la Figura 3-29 desde el infinito hasta su posición en la línea se obtiene de (4) como
\[W = \frac{1}{2} \frac{2q^{2}}{4 \pi \varepsilon a} \bigg[ -1 + \frac{1}{2} - \frac{1}{3} + \frac{1}{4} - \frac{1}{5} + \frac{1}{6} - ... \bigg] \nonumber \]
El factor extra de 2 en el numerador es necesario porque la cadena se extiende hasta el infinito en cada lado. La serie infinita es reconocida como la expansión de la serie Taylor del logaritmo
\[\ln(1 + x) = x - \frac{x^{2}}{2} + \frac{x^{3}}{3} - \frac{x^{4}}{4} + \frac{x^{5}}{5} - ... \nonumber \]
donde x = 1 para que*
\[W = \frac{-q^{2}}{4 \pi \varepsilon a} \ln 2 \nonumber \]
Esta obra es negativa porque el cristal tira de la carga a medida que es traída desde el infinito. Esto significa que se necesitaría un trabajo positivo para eliminar la carga ya que está unida al cristal. Un espaciamiento iónico típico es de aproximadamente 3\(\AA\) (3 x 10 -10 m) de manera que si q es un solo protón (q = 1.6x 10 -19 coul), la energía de unión es\(W \approx 5.3 \times 10^{-19}\) joule. Dado que este número es tan pequeño suele ser más conveniente trabajar con unidades de energía por unidad de carga electrónica llamadas electrón voltios (ev), que se obtienen dividiendo W por la carga en un electrón para que, en este caso,\(W \approx 3.3\) ev.
Si el cristal se colocó en un medio con mayor permitividad, vemos a partir de (7) que la energía de unión disminuye. Es por ello que muchos cristales son solubles en agua, la cual tiene una constante dieléctrica relativa de aproximadamente 80.
3-8-2 Trabajo necesario para formar una distribución continua de carga
No se incluye en (4) la autoenergía de cada carga en sí o, de manera equivalente, el trabajo necesario para ensamblar cada carga puntual. Dado que el potencial V de una carga puntual q es proporcional a q, la autoenergía es proporcional q 2. Sin embargo, evaluar la autoenergía de una carga puntual es difícil porque el potencial es infinito en la carga puntual.
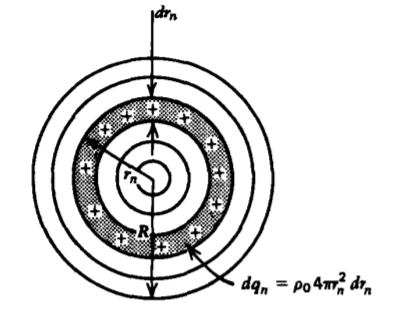
Para entender mejor el concepto de autoenergía ayuda a modelar una carga puntual como un pequeño volumen esférico uniformemente cargado de radio R con carga total\(Q = \frac{4}{3} \pi R^{3} \rho_{0}\). Ensamblamos la esfera de carga a partir de conchas esféricas, como se muestra en la Figura 3-30, cada una de espesor dr n y carga incremental\(dq_{n} = 4 \pi r_{n}^{2}dr_{n}\rho_{0}\). A medida que traemos en el n-ésimo caparazón para ser colocado en el radio r n la carga total ya presente y el potencial que hay
\[q_{n} = \frac{4}{3} \pi r_{n}^{3}\rho_{0}, \: \: \: V_{n} = \frac{q_{n}}{4 \pi \varepsilon r_{n}} = \frac{r_{n}^{2}\rho_{0}}{3 \varepsilon} \nonumber \]
para que el trabajo requerido para traer en el n º shell sea
\[dW_{n} = V_{n} dq_{n} = \frac{\rho_{0}^{2}4 \pi r_{n}^{4}}{3 \varepsilon} dr_{n} \nonumber \]
El trabajo total necesario para ensamblar la esfera se obtiene sumando el trabajo necesario para cada caparazón:
\[W = \int dW_{n} = \int_{0}^{R} \frac{4 \pi \rho_{0}^{2}r^{4}}{3 \varepsilon} dr = \frac{4 \pi \rho_{0}^{2} R^{5}}{15 \varepsilon} = \frac{3Q^{2}}{20 \pi \varepsilon R} \nonumber \]
Para una carga finita Q de radio cero la obra se vuelve infinita. Sin embargo, la teoría de la relatividad de Einstein nos dice que este trabajo necesario para ensamblar la carga se almacena como energía que se relaciona con la masa como
\[W = mc^{2} = \frac{3Q^{2}}{20 \pi \varepsilon R} \Rightarrow R = \frac{3Q^{2}}{20 \pi \varepsilon mc^{2}} \nonumber \]
que luego determina el radio de la carga. Para el caso de un electrón (Q = 1.6 x 10 -19 coul, m = 9.1 x 10 -31 kg) en espacio libre (\(\varepsilon = \varepsilon_{0}\)= 8.854 x 10 -12 farad/m), este radio es
\[R_{\textrm{electron}} = \frac{3(1.6 \times 10^{-19})^{2}}{20 \pi (8.854 \times 10^{-12})(9.1 \times 10^{-31})(3 \times 10^{8})^{2}} \approx 1.69 \times 10^{-15} \textrm{m} \nonumber \]
También podemos obtener el resultado de (10) usando (4) donde cada carga se convierte en un elemento diferencial dq, de manera que la suma se convierte en una integración sobre la distribución continua de carga gratuita:
\[W = \frac{1}{2} \int_{\textrm{all } q_{f}} V \: dq_{f} \nonumber \]
Para el caso de la esfera uniformemente cargada\(dq_{f} = \rho_{0} dV\), el potencial final dentro de la esfera viene dado por los resultados de la Sección 2-5-5b:
\[V = \frac{\rho_{0}}{2 \varepsilon} \bigg( R^{2} - \frac{r^{2}}{3} \bigg) \nonumber \]
Entonces (13) está de acuerdo con (10):
\[W = \frac{1}{2} \int \rho_{0}V dV = \frac{4 \pi \rho_{0}^{2}}{4 \varepsilon} \int_{0}^{R} \bigg(R^{2} - \frac{r^{2}}{3} \bigg)r^{2} dr = \frac{4 \pi \rho_{0}^{2}R^{5}}{15 \varepsilon} = \frac{3 Q^{2}}{20 \pi \varepsilon R} \nonumber \]
Así, en general, definimos (13) como la energía almacenada en el campo eléctrico, incluyendo el término de autoenergía. Se diferencia de (4), que solo incluye términos de interacción entre diferentes cargas y no el trabajo infinito necesario para ensamblar cada carga puntual. La ecuación (13) es válida para distribuciones de carga de línea, superficie y volumen con los elementos de carga diferencial dados en la Sección 2-3-1. Recuerde al usar (4) y (13) que la referencia cero para el potencial se supone que está en el infinito. Agregar un Vo constante al potencial cambiará la energía a menos que la carga total en el sistema sea cero
\[W = \frac{1}{2} \int (V + V_{0}) dq_{f} \\ = \frac{1}{2} \int V dq_{f} + \frac{1}{2} V_{0} \int \dq_{f} \nearrow^{0} \\ = \frac{1}{2} \int V dq_{f} \nonumber \]
* Estrictamente hablando, esta serie sólo es condicionalmente convergente para x = 1 y su suma depende de la agrupación de términos individuales. Si la serie en (6) para x = 1 se reescribe como
\(1 - \frac{1}{2} - \frac{1}{4} + \frac{1}{3} - \frac{1}{6} - \frac{1}{8} + ... + \frac{1}{2k-1} - \frac{1}{4k-2} - \frac{1}{4k} .... k \geq 1\)
entonces su suma es\(\frac{1}{2} \ln 2\). [Véase J. Pleines y S. Mahajan, Sobre series condicionalmente divergentes y una carga puntual entre dos planos paralelos a tierra, Am. J. Phys. 45 (1977) p. 868. ]
3-8-3 Densidad Energética del Campo Eléctrico
También es conveniente expresar la energía W almacenada en un sistema en términos del campo eléctrico. Suponemos que tenemos una distribución de carga volumétrica con densidad\(\rho_{f}\). Entonces,\(dq_{f} = \rho_{f} dV\), donde\(\rho_{f}\) se relaciona con el campo de desplazamiento de la ley de Gauss:
\[W = \frac{1}{2} \int_{\textrm{V}} \rho_{f} V dV = \frac{1}{2} \int_{V} V( \nabla \cdot \textbf{D}) d \textrm{V} \nonumber \]
Examinemos la expansión vectorial
\[\nabla \cdot (V \textbf{D}) = (\textbf{D} \cdot \nabla) V + V(\nabla \cdot \textbf{D}) \Rightarrow V(\nabla \cdot \textbf{D}) = \nabla \cdot (V \textbf{D}) + \textbf{D} \cdot \textbf{E} \nonumber \]
donde\(\textbf{E} = - \nabla V.\) Entonces (17) se convierte
\[W = \frac{1}{2} \int_{\textrm{V}} \textbf{D} \cdot \textbf{E} d \textrm{V} + \frac{1}{2} \int_{\textrm{V}} \nabla \cdot (V \textbf{D}) d \textrm{V} \nonumber \]
El último término en el lado derecho se puede convertir en una integral de superficie usando el teorema de divergencia:
\[\int_{\textrm{V}} \nabla \cdot (V \textbf{D}) d \textrm{V} = \oint_{S} V \textbf{D} \cdot \textbf{dS} \nonumber \]
Si dejamos que el volumen V sea de extensión infinita para que la superficie envolvente S esté en el infinito, la distribución de carga que solo se extiende sobre un volumen finito parece una carga puntual para la cual el potencial disminuye como 1/ r y el vector de desplazamiento muere como\(1/r^{2}\). Así el término, V D en el mejor de los casos muere como 1/ r 2. Entonces, aunque el área superficial de S aumenta a medida que r 2 la integral de superficie tiende a cero a medida que r se vuelve infinito como 1/ r. Así, la segunda integral de volumen en (19) se acerca a cero:
\[\lim_{r \rightarrow \infty} \int_{\textrm{V}} \nabla \cdot (V \textbf{D}) d \textrm{V} = \oint_{S} V \textbf{D} \cdot \textbf{dS} = 0 \nonumber \]
Esta conclusión no es cierta si la distribución de carga es de extensión infinita, ya que para el caso de una carga de línea o superficie infinitamente larga, el potencial mismo se vuelve infinito en el infinito porque la carga total en la línea o superficie es infinita. Sin embargo, para distribuciones de carga de tamaño finito, que siempre es el caso en la realidad, (19) se convierte en
\[W = \frac{1}{2} \int_{\textrm{all space}} \textbf{D} \cdot \textbf{E} d \textrm{V} \\ = \int_{\textrm{all space}} \frac{1}{2} \varepsilon E^{2} d \textrm{V} \nonumber \]
donde la integración se extiende por todo el espacio. Este resultado es cierto incluso si la permitividad\(\varepsilon\) es una función de la posición. Es conveniente definir la densidad de energía como la cantidad definida positiva:
\[w = \frac{1}{2} \varepsilon E^{2} \textrm{joule/m}^{3} [\textrm{kg m}^{-1} \textrm{s}^{-2}] \nonumber \]
donde está la energía total
\[W = \int_{\textrm{all space}} w d \textrm{V} \nonumber \]
Obsérvese que aunque (22) es numéricamente igual a (13), (22) implica que la energía eléctrica existe en aquellas regiones donde existe un campo eléctrico distinto de cero aunque no haya carga presente en esa región, mientras que (13) implica que la energía eléctrica existe solo donde la carga es distinta de cero. La respuesta en cuanto a dónde se almacena la energía -en la distribución de carga o en el campo eléctrico- es cuestión de conveniencia ya que no se puede tener una sin la otra. Numéricamente ambas ecuaciones dan las mismas respuestas pero con contribuciones de diferentes regiones del espacio.
3-8-4 Energía Almacenada en Esferas Cargadas
(a) Carga por volumen
También podemos encontrar la energía almacenada en una esfera de carga uniforme utilizando (22) ya que conocemos el campo eléctrico en cada región a partir de la Sección 2-4-3b. La densidad de energía es entonces
\[w = \frac{\varepsilon}{2} E_{r}^{2} = \left \{ \begin{matrix} \frac{Q^{2}}{32 \pi^{2} \varepsilon r^{4}}, & r>R \\ \frac{Q^{2}r^{2}}{32 \pi^{2} \varepsilon R^{6}} & r<R \right \} \end{matrix} \nonumber \]
con energía total almacenada
\[W = \int_{\textrm{all space}} w d \textrm{V} \\ = \frac{Q^{2}}{8 \pi \varepsilon} \bigg( \int_{0}^{R} \frac{r^{4}}{R^{6}} dr + \int_{R}^{\infty} \frac{dr}{r^{2} \bigg) = \frac{3}{20} \frac{Q^{2}}{\pi \varepsilon R} \nonumber \]
que concuerda con (10) y (15).
(b) Carga superficial
Si la esfera se carga uniformemente en su superficie\(Q = 4 \pi R^{2} \sigma_{0}\), las distribuciones de potencial y campo eléctrico son
\[V(r) = \left \{ \begin{matrix} \frac{Q}{4 \pi \varepsilonR} \\ \frac{Q}{4 \pi \varepsilon r} \end{matrix} \right. E_{r} = \left \{ \begin{matrix} 0, & r<R \\ \frac{Q}{4 \pi \varepsilon r^{2}}, & r>R \end{matrix} \right. \nonumber \]
Usando (22) la energía almacenada es
\[W = \frac{\varepsilon}{2} \bigg(\frac{Q}{4 \pi \varepsilon} \bigg)^{2} 4 \pi \int_{R}^{\infty} \frac{dr}{r^{2}} = \frac{Q^{2}}{8 \pi \varepsilon R} \nonumber \]
Este resultado es igual de fácil obtenido usando (13):
\[W = \frac{1}{2} \int_{S} \sigma_{0} V (r=R) dS \\ = \frac{1}{2} \sigma_{0}V(r=R) 4 \pi R^{2} = \frac{Q^{2}}{8 \pi \varepsilon R} \nonumber \]
La energía almacenada en una esfera con carga uniforme es 20% mayor que la esfera con carga superficial para la misma carga total Q. Esto se debe a la energía adicional almacenada en todo el volumen de la esfera. Fuera de la esfera (r > R) los campos son los mismos que la energía almacenada.
(c) Energía de unión de un átomo
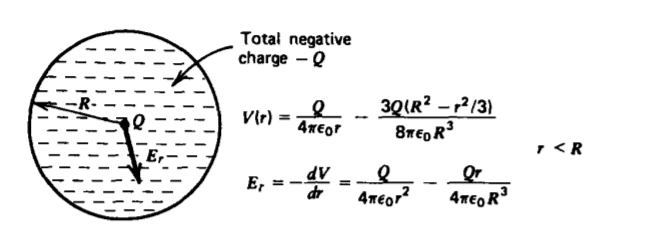
En la Sección 3-1-4 se modeló un átomo como un núcleo Q de carga de punto positivo fijo con una nube esférica uniforme circundante de carga negativa con carga total - Q, como en la Figura 3-31. Los potenciales debidos al punto positivo y las cargas de volumen negativas se encuentran en la Sección 2-5-5b como
\[V_{+}(r) = \frac{Q}{4 \pi \varepsilon_{0}r} \\ V_{-}(r) \left \{ \begin{matrix} -\frac{3Q}{8 \pi \varepsilon_{0}R^{3}} \bigg(R^{2} - \frac{r^{2}}{3}\bigg), & r<R \\ - \frac{Q}{4 \pi \varepsilon_{0}r}, & r>R \end{matrix} \right. \nonumber \]
La energía de unión del átomo se encuentra fácilmente por superposición considerando primero la esfera negativa uniformemente cargada con la autoenergía dada en (10), (15) y (26) y luego agregando la energía de la carga puntual positiva:
\[W = \frac{3Q^{2}}{20 \pi \varepsilon_{0}R} + Q[V - (r=0)] = - \frac{9Q^{2}}{40 \pi \varepsilon_{0}R} \nonumber \]
Este es el trabajo necesario para ensamblar el átomo a partir de cargas al infinito. Una vez que el núcleo positivo está en su lugar, atrae las siguientes cargas negativas para que el campo sí trabaje en las cargas y el trabajo de montaje en (31) sea negativo. Equivalentemente, la magnitud de (31) es el trabajo necesario para que desarmemos el átomo superando las atractivas fuerzas culómbicas entre las cargas de polaridad opuesta.
Al usar alternativamente (4) y (13), solo incluimos el potencial de la carga volumétrica negativa a r = 0 actuando sobre la carga positiva, mientras que incluimos el potencial total debido a ambos en la evaluación de la energía de la carga volumétrica. Nosotros hacemos
no considerar la autoenergía infinita de la carga puntual que se incluiría si usáramos (22):
\[W = \frac{1}{2} QV_{-}(r=0) - \frac{1}{2} \int_{r=0}^{R} [V_{+}(r) + V_{-}(r)] \frac{3Qr^{2}}{R^{3}} dr \\ = - \frac{3Q^{2}}{16 \pi \varepsilon_{0}R} - \frac{3Q^{2}}{8 \pi \varepsilon_{0}R^{3}} \int_{0}^{R} \bigg(r- \frac{3}{2} \frac{r^{2}}{R} + \frac{r^{4}}{2R^{3}}\bigg) dr \\ = - \frac{9Q^{2}}{40 \pi \varepsilon_{0}R} \nonumber \]
3-8-5 Energía almacenada en un condensador
En un condensador toda la carga reside en los electrodos como carga superficial. Considera dos electrodos a voltaje V 1 y V 2 con respecto al infinito, y así a diferencia de voltaje V = V 2 - V 1, como se muestra en la Figura 3-32. Cada electrodo lleva carga de polaridad opuesta con magnitud Q. Entonces (13) se puede usar para calcular la energía total almacenada como
\[W = \frac{1}{2} \bigg[ \int_{S_{1}} V_{1} \sigma_{1} dS_{1} + \int_{S_{2}} V_{2}\sigma_{2} dS_{2} \bigg] \nonumber \]
Dado que cada superficie es un equipotencial, los voltajes V 1 y V 2 pueden tomarse fuera de las integrales. La integral entonces reduce a la carga total\(\pm Q\) en cada electrodo:
\[W = \frac{1}{2} \bigg[ V_{1} \int_{S_{1}} \underbrace{\sigma_{1} dS_{1}}_{-Q} + V_{2} \int_{S_{2}} \underbrace{\sigma_{2}dS_{2}}_{Q} \bigg] = \frac{1}{2}(V_{2}-V_{1})Q = \frac{1}{2}QV \nonumber \]
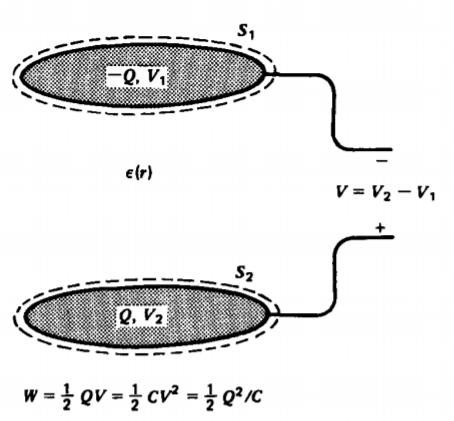
Dado que en un condensador la carga y el voltaje están linealmente relacionados a través de la capacitancia
\[Q = CV \nonumber \]
la energía almacenada en el condensador también se puede escribir como
\[W = \frac{1}{2} QV = \frac{1}{2} CV^{2} = \frac{1}{2} \frac{Q^{2}}{C} \nonumber \]
Esta energía es equivalente a (22) en términos del campo eléctrico y nos da un método alternativo para calcular la capacitancia si conocemos la distribución del campo eléctrico.
Una esfera de radio R lleva una carga superficial Q uniformemente distribuida. ¿Cuál es su capacitancia?
- Responder
-
La energía almacenada viene dada por (28) o (29) de manera que (36) nos da la capacitancia:
\[C = Q^{2}/2W = 4 \pi \varepsilon R \nonumber \]


