3.9: Campos y sus Fuerzas

3-9-1 Fuerza por unidad de área sobre una hoja de carga superficial

Surge una confusión al aplicar la ley de Coulomb para encontrar la fuerza perpendicular sobre una lámina de carga superficial ya que el campo eléctrico normal es diferente en cada lado de la lámina. Usando el argumento sobresimplificado de que la mitad de la carga superficial reside en cada lado de la hoja produce la fuerza correcta

\[\textbf{F} = \frac{1}{2} \int_{S} \sigma_{f} (\textbf{E}_{1} + \textbf{E}_{2}) d \textrm{S} \nonumber \]

donde, como se muestra en la Figura 3-33a, E ₁ y E ₂ son los campos eléctricos a cada lado de la lámina. Así, el campo correcto a utilizar es el campo eléctrico promedio\(\frac{1}{2}(\textbf{E}_{1} + \textbf{E}_{2})\) a través de la lámina.

Para la fuerza tangencial, los componentes tangenciales de E son continuos a través de la lámina (\(E_{1t} = E_{2t} \approx E_{t}\)) de manera que

\[f_{t} = \frac{1}{2} \int_{S} \sigma_{f}(E_{1t} + E_{2t}) d \textrm{S} = \int_{S} \sigma_{f}E_{t} d \textrm{S} \nonumber \]

Figura 3-33 (a) El componente normal del campo eléctrico es discontinuo a través de la lámina de carga superficial. (b) La lámina de carga superficial puede modelarse como una capa delgada de carga volumétrica. El campo eléctrico entonces varía linealmente a través del volumen.

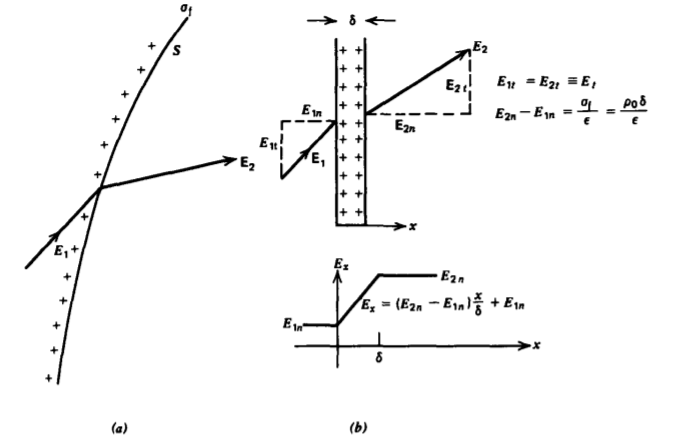
Los campos normales son discontinuos a través de la hoja para que la fuerza perpendicular sea

\[\sigma_{f} = \varepsilon (E_{2n} - E_{1n}) \Rightarrow f_{n} = \frac{1}{2} \int_{S} \varepsilon (E_{2n}-E_{1n})(E_{1n} + E_{2n}) d \textrm{S} \\ = \frac{1}{2} \int_{S} \varepsilon (E_{2n}^{2} - E_{1n}^{2})d \textrm{S} \nonumber \]

Para ser matemáticamente rigurosos podemos examinar más de cerca la transición de campo a través de la lámina asumiendo que la carga superficial es realmente una distribución uniforme de carga volumétrica\(\rho_{0}\) de espesor muy estrecho\(\delta\), como se muestra en la Figura 3-33b. Sobre el elemento superficial pequeño d S, la superficie aparece recta de manera que el campo eléctrico debido a la carga de volumen solo puede variar con la coordenada x perpendicular a la superficie. Entonces la forma puntual de la ley de Gauss dentro de los rendimientos de volumen

\[\frac{dE_{x}}{dx} = \frac{\rho_{0}}{\varepsilon} \Rightarrow E_{x} = \frac{\rho_{0}x}{\varepsilon} + \textrm{const} \nonumber \]

La constante en (4) es evaluada por las condiciones límite en los componentes normales del campo eléctrico en cada lado de la lámina

\[E_{x}(x=0) = E_{1n}, \: \: \: \: \: E_{x}(x = \delta) = E_{2n} \nonumber \]

para que el campo eléctrico sea

\[E_{x} = (E_{2n} - E_{1n}) \frac{x}{\delta} + E_{1n} \nonumber \]

A medida que el espesor de la losa\(\delta\) se vuelve muy pequeño, nos acercamos a una carga de lámina que relaciona la densidad de carga superficial con la discontinuidad en campos eléctricos como

\[\lim_{\rho_{0} \rightarrow \infty \\ \delta \rightarrow 0} \rho_{0} \delta = \sigma_{f} = \varepsilon (E_{2n} - E_{1n}) \nonumber \]

De igual manera la fuerza por unidad de área sobre la losa de carga volumétrica es

\[F_{x} = \int_{0}^{|delta} \rho_{0}E_{x}dx \\ = \int_{0}^{\delta} \rho_{0} \bigg[ (E_{2n} - E_{1n}) \frac{x}{\delta} + E_{1n} \bigg] dx \\ = \bigg[ \rho_{0} (E_{2n} - E_{1n}) \frac{x^{2}}{2 \delta} + E_{1n}x \bigg] \bigg|_{0}^{\delta} \\ = \frac{\rho_{0} \delta}{2} (E_{1n} + E_{2n}) \nonumber \]

En el límite de (7), la fuerza por unidad de área sobre la lámina de carga superficial concuerda con (3):

\[\lim_{\rho_{0} \delta = \sigma_{f}} F_{x} = \frac{\sigma_{f}}{2}(E_{1n} + E_{2n}) = \frac{\varepsilon}{2} (E_{2n}^{2} -E_{1n}^{2}) \nonumber \]

3-9-2 Fuerzas en un Medio Polarizado

(a) Densidad de Fuerza

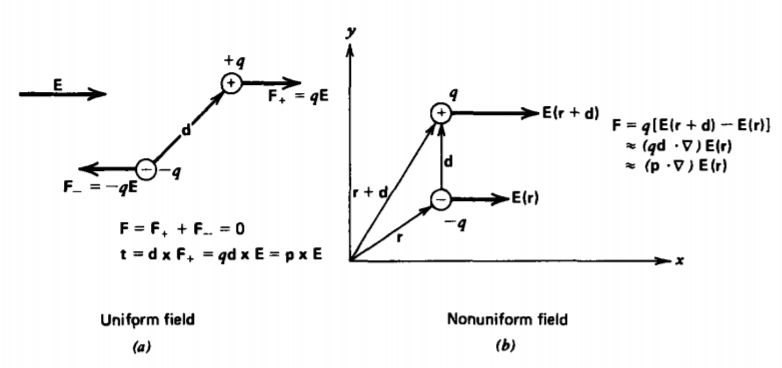
En un campo eléctrico uniforme no hay fuerza sobre un dipolo porque la fuerza sobre cada carga es igual en magnitud pero opuesta en dirección, como en la Figura 3-34a. Sin embargo, si el momento dipolar no está alineado con el campo hay un par de alineación dado por t = p x E. El par por unidad de volumen T en un medio polarizado con N dipolos por unidad de volumen es entonces

\[\textbf{T} = N \textbf{t} = N \textbf{p} \times \textbf{P} \times \textbf{E} \nonumber \]

Figura 3-34 (a) Un par es percibido por un dipolo si su momento no está alineado con el campo eléctrico. En un campo eléctrico uniforme no hay fuerza neta sobre un dipolo porque la fuerza en cada carga es igual en magnitud pero opuesta en dirección. b) Hay una fuerza neta sobre un dipolo sólo en un campo no uniforme.

Para un dieléctrico lineal, este par es cero debido a que la polarización es inducida por el campo de manera que P y E están en la misma dirección.

Se puede aplicar una fuerza neta a un dipolo si el campo eléctrico es diferente en cada extremo, como en la Figura 3-34b:

\[\textbf{f} = -q[\textbf{E}(\textbf{r}) - \textbf{E}(\textbf{r} + \textbf{d})] \nonumber \]

Para los dipolos puntuales, el espaciamiento de dipolos d es muy pequeño de manera que el campo eléctrico a r + d se puede expandir en una serie Taylor como

\[\textbf{E}(\textbf{E} + \textbf{d}) \approx \textbf{E} (\textbf{r}) + d_{x} \frac{\partial}{\partial x} \textbf{E} (\textbf{r}) + d_{y} \frac{\partial}{\partial y} \textbf{E}(\textbf{r}) + d_{z} \frac{\partial}{\partial z} \textbf{E}(\textbf{r}) = \textbf{E}(\textbf{r}) + (\textbf{d} \cdot \nabla) \textbf{E}(\textbf{r}) \nonumber \]

Entonces la fuerza sobre un dipolo puntual es

\[\textbf{f} = (q \textbf{d} \cdot \nabla) \textbf{E}(\textbf{r}) = (\textbf{p} \cdot \nabla) \textbf{E}(\textbf{r}) \nonumber \]

Si tenemos una distribución de dichos dipolos con densidad numérica N, la densidad de fuerza de polarización es

\[\textbf{F} + N \textbf{f} = (N \textbf{p} \cdot \nabla) \textbf{E} = (\textbf{P} \cdot \nabla) \textbf{E} \nonumber \]

Por supuesto, si hay algún cargo libre presente también debemos agregar la densidad de fuerza coulómbica\(\rho_{f} \textbf{E}\).

(b) Polarizado Permanentemente Medio

Un material permanentemente polarizado con polarización\(P_{0}\textbf{i}\), es libre de deslizarse entre electrodos de placa paralelos, como se muestra en la Figura 3-35.

Figura 3-35 (a) Un electreto permanentemente polarizado parcialmente insertado en un condensador tiene una fuerza sobre él debido a la atracción coulómbica entre las cargas dipolares y la carga superficial en los electrodos. La fuerza neta surge en la región del campo marginal ya que el extremo del dipolo más alejado del borde del electrodo siente un campo eléctrico más pequeño. Dependiendo de la magnitud del voltaje y la polaridad, el electreto puede extraerse o extraerse del condensador. (b) Un dieléctrico lineal siempre es atraído hacia un condensador de espacio libre debido a la fuerza neta sobre los dipolos en el campo no uniforme. Los dipolos ahora están alineados con el campo eléctrico, sin importar la polaridad del voltaje

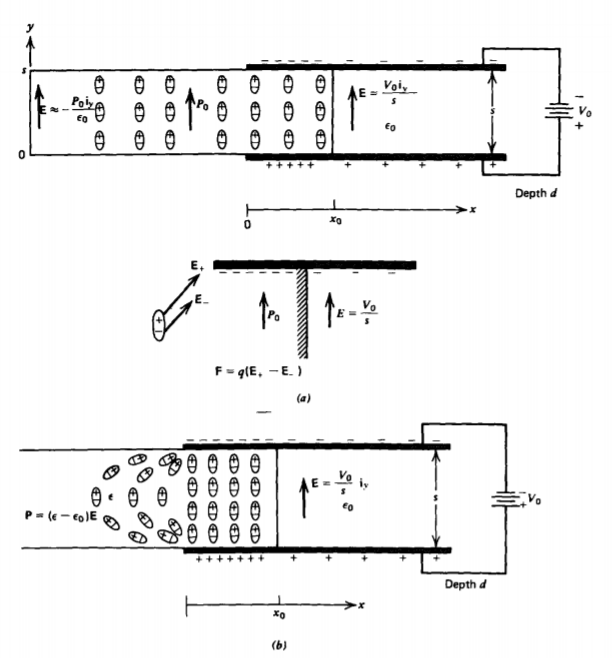
Solo conocemos el campo eléctrico en la región interelectrodo y del Ejemplo 3-2 lejos de los electrodos:

\[E_{y} (x = x_{0}) = \frac{V_{0}}{s}, \: \: \: E_{y}(x = - \infty) = - \frac{P_{0}}{\varepsilon_{0}} \nonumber \]

Desafortunadamente, ninguna de estas regiones contribuye a la fuerza porque el campo eléctrico es uniforme y (14) requiere un gradiente de campo para una fuerza. La fuerza surge en los campos de franjas cerca de los bordes del electrodo donde el campo no es uniforme y, por lo tanto, ejerce menos fuerza sobre el extremo del dipolo más alejado de los bordes del electrodo. A primera vista parece que tenemos un problema difícil porque desconocemos los campos donde actúa la fuerza. Sin embargo, debido a que el campo eléctrico tiene cero rizo,

\[\nabla \times \textbf{E} = 0 \Rightarrow \frac{\partial E_{x}}{\partial y} = \frac{\partial E_{y}}{\partial x} \nonumber \]

el componente x de la densidad de fuerza se puede escribir como

\[F_{x} =P_{y} \frac{\partial E_{x}}{\partial y} \\ = P_{y} \frac{\partial E_{y}}{\partial x} \\ = \frac{\partial}{\partial x} (P_{y}E_{y})-E_{y} \frac{\partial P_{y}}{\partial x} \nearrow^{0} \nonumber \]

El último término en (17) es cero porque\(P_{y} =P_{0}\) es una constante. La fuerza total x dirigida es entonces

\[f_{x} = \int F_{x} dx dy dz \\ = \int_{x = i \infty}^{x_{0}} \int_{y=0}^{s} \int_{z = 0}^{d} \frac{\partial}{\partial x} (P_{y}E_{y}) dx dy dz \nonumber \]

Primero hacemos la integración x para que las integraciones y y z sean multiplicaciones simples ya que los campos en los límites de la integración x son independientes de y y z:

\[f_{x} = P_{0}E_{y}sd \|_{x= - \infty}^{x_{0}} = P_{0}V_{0}d + \frac{P_{0}^{2}sd}{\varepsilon_{0}} \nonumber \]

Hay una fuerza que tira del electreto entre los electrodos aunque el voltaje fuera cero debido al campo generado por la carga superficial en los electrodos inducida por el electreto. Esta fuerza se incrementa si el campo eléctrico impuesto y la polarización están en la misma dirección. Si se invierte la polaridad del voltaje, la fuerza es negativa y el electreto es empujado hacia afuera si la magnitud del voltaje excede\(P_{0}s/\varepsilon_{0}\).

(c) Polarizado Linealmente Medio

El problema es diferente si la losa está polarizada por el campo eléctrico, ya que la polarización será entonces en la dirección del campo eléctrico y así tendrá componentes x e y en los campos de franjas cerca de los bordes del electrodo donde surge la fuerza, como en la Figura 3-35b. Los dipolos tienden a alinearse como se muestra con los extremos positivos atraídos hacia el electrodo negativo y el dipolo negativo termina hacia el electrodo positivo. Debido a que los extremos más alejados de los dipolos están en un campo ligeramente más débil, hay una fuerza neta hacia la derecha que tiende a atraer el dieléctrico hacia el condensador.

La densidad de fuerza de (14) es

\[F_{x} = P_{x} \frac{\partial E_{x}}{\partial x} + P_{y} \frac{\partial E_{x}}{\partial y} = (\varepsilon - \varepsilon_{0}) \bigg( E_{x} \frac{\partial E_{x}}{\partial x} + E_{y} \frac{\partial E_{x}}{\partial y} \bigg) \nonumber \]

Debido a que el campo eléctrico está libre de rizos, como se indica en (16), la densidad de fuerza se simplifica aún más para

\[F_{x} = \frac{(\varepsilon- \varepsilon_{0})}{2} \frac{\partial}{\partial x}(E_{x}^{2} + E_{y}^{2}) \nonumber \]

La fuerza total se obtiene integrando (21) sobre el volumen del dieléctrico:

\[f_{x} = \int_{X = - \infty}^{x_{0}} \int_{y=0}^{s} \int_{z=0}^{d} \frac{(\varepsilon - \varepsilon_{0})}{2} \frac{\partial}{\partial x} (E_{x}^{2} + E_{y}^{2}) dx dy dz \\ = \frac{(\varepsilon - \varepsilon_{0})sd}{2} (E_{x}^{2} + E_{y}^{2}) \|_{x = - \infty}^{x_{0}} = \frac{(\varepsilon - \varepsilon_{0})}{2} \frac{V_{0}^{2}d}{s} \nonumber \]

donde sabíamos que los campos eran cero en\(x = - \infty\) y uniformes en\(x = x_{0}\):

\[E_{y}(x_{0}) = V_{0}/s, \: \: \: E_{x}(x_{0}) = 0 \nonumber \]

La fuerza ahora es independiente de la polaridad del voltaje y siempre actúa en la dirección para tirar del dieléctrico hacia el condensador si\(\varepsilon > \varepsilon_{0}\)

3-9-3 Fuerzas en un Capacitor

Considera un condensador que tenga una parte que pueda moverse en la dirección x para que la capacitancia dependa de la coordenada x:

\[q = C(x)v \nonumber \]

La corriente se obtiene diferenciando la carga respecto al tiempo:

\[i = \frac{dq}{dt} = \frac{d}{dt} [C(x)v] = C(x) \frac{dv}{dt} + v \frac{dC(x)}{dt} = C(x) \frac{dv}{dt} + v \frac{dC(x)}{dx} \frac{dx}{dt} \nonumber \]

Obsérvese que esta relación tiene un término extra sobre la fórmula habitual del circuito, proporcional a la velocidad del miembro móvil, donde expandimos la derivada de tiempo de la capacitancia por la regla de la cadena de diferenciación. Por supuesto, si la geometría es fija y no cambia con el tiempo (dx/dt = 0), entonces (25) reduce a la expresión habitual del circuito. El último término se debe al acoplamiento electromecánico.

La potencia suministrada a una capacitancia dependiente del tiempo es

\[p = v \textbf{i} = v \frac{d}{dt}[C(x)v] \nonumber \]

que se puede ampliar a la forma

\[p = \frac{d}{dt}[\frac{1}{2} C(x)v^{2}] + \frac{1}{2}v^{2}\frac{dC(x)}{dt} \\ = \frac{d}{dt} [\frac{1}{2} C (x)v^{2}] + \frac{1}{2} v^{2} \frac{dC(x)}{dx} \frac{dx}{dt} \nonumber \]

donde nuevamente se obtiene el último término usando la regla de diferenciación en cadena. Esta expresión se puede poner en la forma

\[p = \frac{dW}{dt} + f_{x}\frac{dx}{dt} \nonumber \]

donde identificamos la potencia p entregada al condensador como la que va a aumentar el almacenamiento de energía W y la potencia\(f_{x} dx/dt\) mecánica al mover una parte del condensador:

\[W = \frac{1}{2} C(x) v^{2}, \: \: \: \: f_{x} = \frac{1}{2} v^{2} \frac{dC(x)}{dx} \nonumber \]

Usando (24), la energía almacenada y la fuerza también se pueden expresar en términos de la carga como

\[W = \frac{1}{2} \frac{q^{2}}{C(x)}, \: \: \: f_{x} = \frac{1}{2} \frac{q^{2}}{C^{2}(x)} \frac{dC(x)}{dx} = - \frac{1}{2}q^{2} \frac{d[1/C(x)]}{dx} \nonumber \]

Para ilustrar la facilidad de usar (29) o (30) para encontrar la fuerza, considere nuevamente el dieléctrico parcialmente insertado en la Figura 3-35b. La capacitancia cuando el dieléctrico se extiende una distancia x en los electrodos es

\[C(x) = \frac{\varepsilon x d}{s} + \varepsilon_{0}\frac{(l-x)d}{s} \nonumber \]

para que la fuerza sobre el dieléctrico dada por (29) concuerde con (22):

\[f_{x} = \frac{1}{2} V_{0}^{2} \frac{dC(x)}{dx} = \frac{1}{2}(\varepsilon - \varepsilon_{0}) \frac{V_{0}^{2}d}{s} \nonumber \]

Nótese que descuidamos las contribuciones del campo marginal a la capacitancia en (31) a pesar de que son el origen físico de la fuerza. Los resultados coinciden porque esta capacitancia extra no depende de la posición x del dieléctrico cuando x está lejos de los bordes del electrodo.

Este método sólo puede ser utilizado para sistemas dieléctricos lineales descritos por (24). No es válido para el problema de electreto tratado en la Sección 3-9-2b debido a que la carga del electrodo no está linealmente relacionada con el voltaje, siendo en parte inducida por el electreto.

Ejemplo 3-4: Fuerza sobre un condensador de placa paralela

En la Figura 3-36 se muestran dos electrodos paralelos perfectamente conductores del área A y una distancia x de separación. Para cada una de las dos configuraciones siguientes, encuentre la fuerza sobre el electrodo superior en la dirección x cuando el sistema esté restringido a voltaje constante V _o o carga constante Q _o.

Figura 3-36 Un condensador de placa paralela (a) sumergido dentro de un fluido dieléctrico o con (b) una región de espacio libre en serie con un dieléctrico sólido.

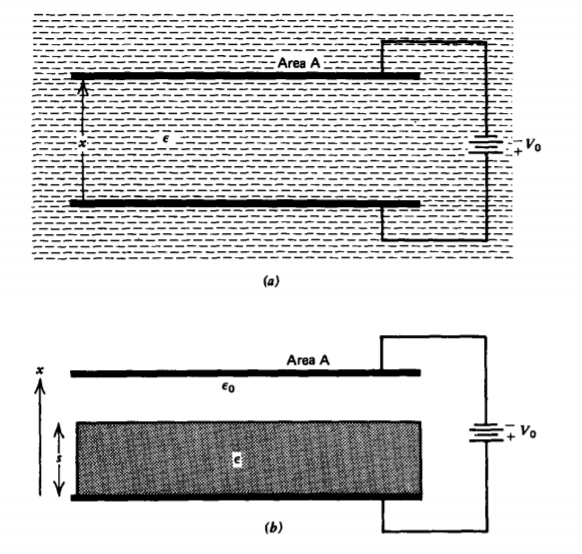
(a) Dieléctrico líquido

Los electrodos se sumergen dentro de un dieléctrico líquido con permitividad\(\varepsilon\), como se muestra en la Figura 3-36a.

b) Dieléctrico sólido

Un dieléctrico sólido con permitividad e de espesor s se inserta entre los electrodos con el resto del espacio teniendo permitividad eo, como se muestra en la Figura 3-36b.

Contestar

a) La capacitancia del sistema es

\(C(x) = \varepislon A/x\)

para que la fuerza de (29) para voltaje constante sea

\(f_{x} = \frac{1}{2} V_{0}^{2} \frac{dC(x)}{dx} = - \frac{1}{2} \frac{\varepsilon A V_{0}^{2}}{x^{2}}\)

El hecho de que la fuerza sea negativa significa que está en la dirección opuesta a aumentar x, en este caso hacia abajo. Las placas del condensador se atraen entre sí porque están cargadas de manera opuesta y las cargas opuestas se atraen. La fuerza es independiente de la polaridad del voltaje y se vuelve infinitamente grande a medida que la distancia entre placas se acerca a cero El resultado también es válido para espacio libre con\(\varepsilon = \varepsilon_{0}\). La presencia del dieléctrico aumenta la fuerza de atracción.

Si los electrodos están limitados a una carga constante Q _o la fuerza es entonces atractiva pero independiente de x:

\(f_{x} = - \frac{1}{2} Q_{0}^{2} \frac{d}{dx} \frac{1}{C(x)}= - \frac{1}{2} \frac{Q_{0}^{2}}{\varepsilon A}\)

Para ambos casos, el valor numérico de la fuerza es el mismo porque Qo y Vo están relacionados por la capacitancia, pero la dependencia funcional de x es diferente. La presencia de un dieléctrico ahora disminuye la fuerza sobre la del espacio libre.

b) Dieléctrico sólido

Un dieléctrico sólido con permitividad\(\varepsilon\) de espesor s se inserta entre los electrodos con el resto del espacio teniendo permitividad\(\varepsilon\), como se muestra en la Figura 3-36b.

La capacitancia total para esta configuración viene dada por la combinación en serie de capacitancia debida al bloque dieléctrico y la región de espacio libre:

\[C(x) = \frac{\varepsilon \varepsilon_{0}A}{\varepsilon_{0}s + \varepsilon (x-s)} \nonumber \]

La fuerza en el electrodo superior para voltaje constante es

\[f_{x} = \frac{1}{2} V_{0}^{2} \frac{d}{dx} C(x) = - \frac{\varepsilon^{2} \varepsilon_{0}A V_0^{2}}{2 [\varepsilon_{0}s + \varepsilon(x-s)]^{2}} \nonumber \]

Si el electrodo simplemente descansa sobre el dieléctrico para que x = s, la fuerza es

\[f_{x}= - \frac{\varepsilon^{2}AV_{0}^{2}}{2 \varepsilon_{0}s^{2}}. \nonumber \]

Este resultado difiere del de la parte (a) cuando x = s por el factor\(\varepsilon_{r}= \varepsilon/\varepsilon_{0}\) porque en este caso mover el electrodo incluso ligeramente fuera del dieléctrico deja una región de espacio libre en el medio. En la parte (a) no se desarrolla hueco de espacio libre a medida que el dieléctrico líquido llena la región, de manera que el dieléctrico siempre está en contacto con el electrodo. La fuerza total en la interfaz electrodo-dieléctrico se debe tanto a la carga libre como a la carga de polarización

Con los electrodos restringidos a carga constante, la fuerza sobre el electrodo superior es independiente de la posición y también independiente de la permitividad del bloque dieléctrico:

\[f_{x} = - \frac{1}{2}Q_{0}^{2} \frac{d}{dx} \frac{1}{C(x)} = - \frac{1}{2} \frac{Q_{0}^{2}}{\varepsilon_{0}A} \nonumber \]