3.10: Generadores Electrostáticos

3-10-1 Generador Van de Graaff

En la década de 1930, se necesitaban medios confiables de generar altos voltajes para acelerar las partículas cargadas en estudios atómicos. En 1931, Van de Graaff desarrolló un generador electrostático donde la carga se rocía sobre una cinta móvil aislante que transporta esta carga sobre una cúpula conductora, como se ilustra en la Figura 3-37a. Si la cúpula se consideró una esfera aislada de radio R, la capacitancia se da como\(C= 4 \pi \varepsilon_{0}R\). La carga transportada actúa como fuente de corriente alimentando esta capacitancia, como en la Figura 3-37b, de manera que el voltaje de la cúpula se acumula linealmente con el tiempo:

\[i = C \frac{dv}{dt} \Rightarrow v = \frac{i}{C}t \nonumber \]

Este voltaje aumenta hasta que se alcanza la resistencia a la ruptura de la atmósfera circundante, con lo cual se produce una descarga de chispa. En el aire, la intensidad de ruptura del campo eléctrico E _b es de 3 x 10 ⁶ V/m El campo cerca de la cúpula varía como\(E_{r} = VR/r^{2}\) que es máximo a r = R, lo que implica un voltaje máximo de V _max = E _b R. Para V _max = 10 ⁶ V, el radio de la esfera

Figura 3-37 (a) Un generador Van de Graaff consiste en una cinta aislante móvil que transporta carga inyectada sobre una cúpula conductora que puede elevarse así a tensiones muy altas, fácilmente superiores a un millón de voltios. (b) Un circuito equivalente simple consiste en la carga de convección modelada como una fuente de corriente que carga la capacitancia del domo.

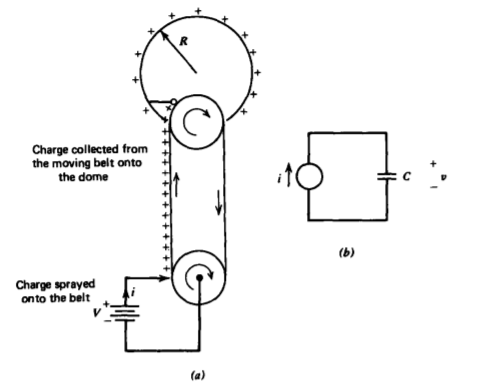
debe ser\(R \approx \frac{1}{3}\) mi para que la capacitancia sea\(C \approx 37\) pf. Con una corriente de carga de un microamperio, se necesitan\(t \approx 37\) segundos para alcanzar este voltaje máximo.

3-10-2 Máquinas de inducción electrostática autoexcitada

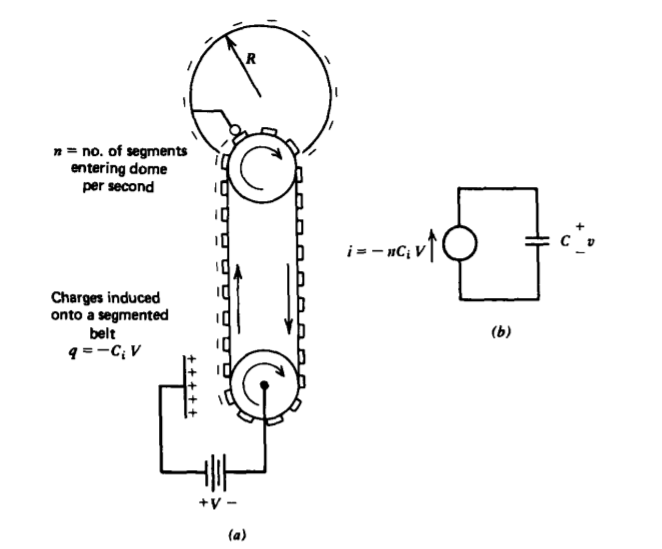
En el generador Van de Graaff, es necesaria una fuente de voltaje externa para depositar carga en la correa. A finales de 1700, se desarrollaron máquinas de inducción electrostática autoexcitada que no requerían ninguna fuente eléctrica externa. Para entender cómo funcionan estos dispositivos, modificamos la configuración del generador Van de Graaff, como en la Figura 3-38a, colocando segmentos conductores en la cinta aislante. En lugar de rociar carga, colocamos un electrodo a voltaje V con respecto a la polea conductora inferior para que se induzca carga de polaridad opuesta en los segmentos móviles. A medida que los segmentos se mueven fuera de la polea, llevan su carga con ellos. Hasta el momento, este dispositivo es similar al generador Van de Graaff usando carga inducida en lugar de carga pulverizada y es descrito por el mismo circuito equivalente donde la fuente de corriente ahora depende de la capacitancia _Ci entre el electrodo inductor y los electrodos segmentados, como en Figura 3-38b.

Figura 3-38 Un generador Van de Graaff modificado como máquina de inducción electrostática. (a) Aquí se inducen cargas sobre una correa segmentada que lleva conductores aislados a medida que la correa pasa cerca de un electrodo a voltaje V. (b) Ahora la fuente de corriente que alimenta el circuito equivalente del condensador depende de la capacitancia _Ci entre el electrodo y la correa.

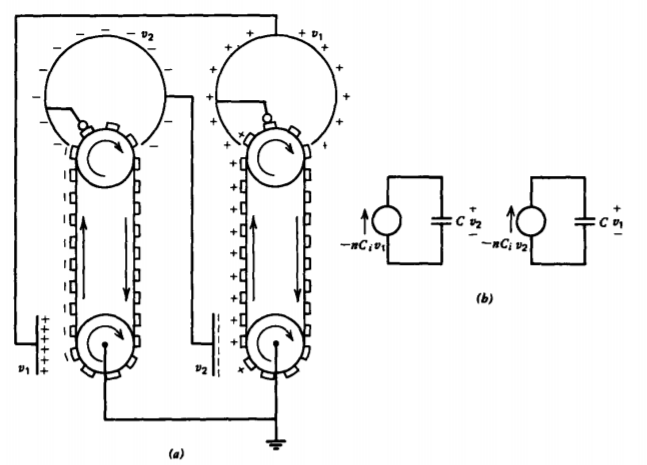
Ahora los primeros investigadores colocaron inteligentemente otra máquina de inducción cerca como en la Figura 3-39a. En lugar de aplicar una fuente de voltaje, debido a que una aún no había sido inventada, conectaban eléctricamente la cúpula de cada máquina al electrodo inductor de la otra. La carga inducida en una máquina fue proporcional a la tensión en la otra cúpula. Aunque no se aplica voltaje, cualquier desequilibrio de carga en un electrodo inductor debido a ruido aleatorio o carga parásita inducirá una carga opuesta en la correa segmentada móvil que lleva esta carga a la cúpula de la cual algunas aparecen en el otro electrodo inductor donde el proceso se repite con opuesto carga de polaridad. El efecto neto es que se ha incrementado la carga sobre el inductor original.

Más cuantitativamente, utilizamos el par de circuitos equivalentes en la Figura 3-39b para obtener las ecuaciones acopladas

\[-nC_{i}v_{1} = C \frac{dv_{2}}{dt}, \: \: \: \: -nC_{i}v_{2} = C \frac{dv_{1}}{dt} \nonumber \]

donde n es el número de segmentos por segundo que pasan a través de la cúpula. Todos los voltajes están referenciados a las poleas inferiores que están conectadas eléctricamente entre sí. Debido a que estos

Figura 3-39 (a) Un par de máquinas de inducción electrostática autoexcitadas acopladas generan su propio voltaje inductor. b) El sistema es descrito por dos circuitos simples acoplados.

son ecuaciones diferenciales de coeficiente constante lineal, las soluciones deben ser exponenciales:

\[v_{1} = \hat{\textrm{V}}_{1}e^{st}, \: \: \: \: v_{2} = \hat{\textrm{V}}_{2}e^{st} \nonumber \]

Sustituir estas soluciones supuestas en (2) produce las siguientes raíces características:

\[s^{2} = \bigg(\frac{nC_{i}}{C}\bigg)^{2} \Rightarrow s = \pm \frac{nC_{i}}{C} \nonumber \]

para que la solución general sea

\[v_{1} = A_{1}e^{(nC_{i}/C)t} + A_{2}e^{-(nC_{i}/C)t} \\ v_{2}= -A_{1}e^{(nC_{i}/C)t} + A_{2}e^{-(nC_{i}/C)t} \nonumber \]

donde A ₁ y _A2 se determinan a partir de las condiciones iniciales.

La raíz negativa de (4) representa las soluciones en descomposición poco interesantes mientras que la raíz positiva tiene soluciones que crecen sin límites con el tiempo. Es por ello que la máquina está autoexcitada. Cualquier perturbación de voltaje inicial, por pequeña que sea, aumenta sin límite hasta que se alcanza la avería eléctrica. Usando valores representativos de n = 10, C _i = 2 pf y C = 10 pf, tenemos eso para\(s = \pm 2\) que la constante de tiempo para la acumulación de voltaje sea de aproximadamente medio segundo.

Figura 3-39b.

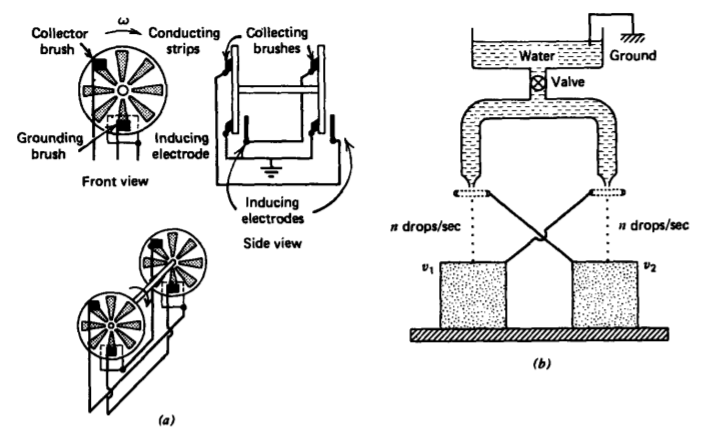
Los primeros científicos eléctricos no utilizaron una cinta segmentada sino discos conductores incrustados en una rueda aislante que se podían girar a mano, como se muestra para la máquina de Wimshurst en la Figura 3-40a. Utilizaron el voltaje de crecimiento exponencial para cargar un condensador llamado tarro de Leyden (acreditado a científicos de Leyden, Holanda), que era una botella de vidrio plateada por dentro y por fuera para formar dos electrodos con el vidrio como dieléctrico.

Un dínamo análogo de gotas de agua fue inventado por Lord Kelvin (entonces Sir W. Thomson) en 1861, que reemplazó los discos giratorios por gotas de agua que caían, como en la Figura 3-40b. Todos estos dispositivos son descritos por los circuitos equivalentes acoplados en la Figura 3-39b.

3-10-3 Voltajes alternos trifásicos autoexcitados

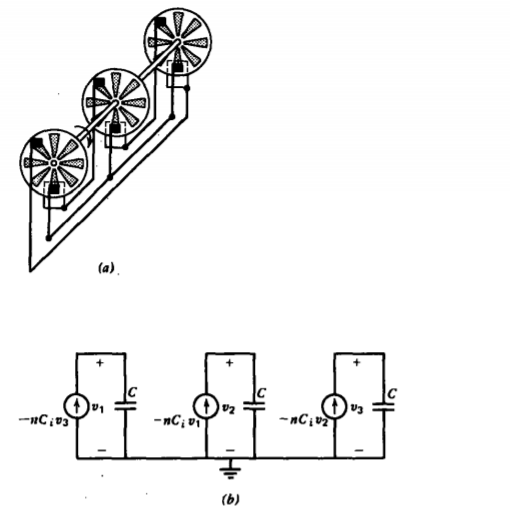
En 1967, Euerle* modificó la dinamo original de Kelvin añadiendo una tercera corriente de gotas de agua para que se generaran tensiones alternas trifásicas. La máquina Wimshurst trifásica análoga se dibuja en la Figura 3-41a con circuitos equivalentes en la Figura 3-41b. Procediendo como lo hicimos en (2) y (3),

\[\begin{matrix} -nC_{i}v_{1}=C\frac{dv_{2}}{dt}, & v_{1} = \hat{\textrm{V}}_{1}e^{st} \\ -nC_{i}v_{2}=C \frac{dv_{3}}{dt}, & v_{2}= \hat{\textrm{V}}_{2}e^{st} \\ -nC_{i}v_{3}=C \frac{dv_{1}}{dt}, & v_{3} = \hat{\textrm{V}}_{3}e^{st} \end{matrix} \nonumber \]

ecuación (6) se puede reescribir como

\[ \left[ \begin{matrix} nC_{i} & C_{s} & 0 \\ 0 & nC_{i} & C_{s} \\ C_{s} & 0 & nC_{i} \end{matrix} \right] \left[ \begin{matrix} \hat{\textrm{V}}_{1} \\ \hat{\textrm{V}}_{2} \\ \hat{\textrm{V}}_{3} \end{matrix} \right] = 0 \nonumber \]

Figura 3-41 (a) Máquina Wimshurst ac trifásica autoexcitada. (b) El circuito equivalente acoplado es válido para cualquiera de las máquinas análogas discutidas.

que requiere que el determinante de los coeficientes de\(\hat{\textrm{V}}_{1}\),\(\hat{\textrm{V}}_{2}\), y\(\hat{\textrm{V}}_{3}\) sea cero:

\[(nC_{i})^{3} + (cs)^{3} = 0 \Rightarrow s = \bigg(\frac{nC_{i}}{C} \bigg)^{1/3} (-1)^{1/3} \\ = \bigg(\frac{nC_{i}}{C} \bigg)^{1/3} e^{j(\pi/3)(2r-1)}, \: \: \: r = 1, 2, 3 \\ \Rightarrow s_{1} = - \frac{nC_{i}}{C} \\ s_{2,3} = \frac{nC_{i}}{2C}[1 \pm \sqrt{3}j] \nonumber \]

donde nos dimos cuenta de que (- 1) ^1/3 tiene tres raíces en el plano complejo. La primera raíz es una solución exponencialmente en descomposición, pero las otras dos son conjugados complejos donde la parte real positiva significa crecimiento exponencial con el tiempo mientras que la parte imaginaria da la frecuencia de oscilación. Contamos con un generador trifásico autoexcitado ya que cada voltaje para los modos inestables está separado 120° en fase de los demás:

\[\frac{\hat{\textrm{V}}_{2}}{\hat{\textrm{V}}_{1}} = \frac{\hat{\textrm{V}}_{3}}{\hat{\textrm{V}}_{2}}={\hat{\textrm{V}}_{1}}{\hat{\textrm{V}}_{3}} = - \frac{nC_{i}}{Cs_{2,3}} = -\frac{1}{2}(1 \pm \sqrt{3}j) = e^{\pm j(2/3) \pi} \nonumber \]

Usando nuestros valores típicos anteriores siguientes (5), vemos que las frecuencias de oscilación son muy bajas,\(f = (1/2 \pi)\) Im (s)\(\approx\) 0.28 Hz.

* W C. Euerle, “Un método novedoso de generación de energía polifásica”, Tesis M.S., Instituto Tecnológico de Massachusetts, 1967. Véase también J. R. Melcher, Campos eléctricos y medios móviles, IEEE Trans. Educación E-17 (1974), pp. 100-110, y la película del mismo título producida para el Comité Nacional de Películas de Ingeniería Eléctrica por el Centro de Desarrollo Educativo, 39 Chapel St., Newton, Misa. 02160.

3-10-4 Generadores multifrecuencia autoexcitados

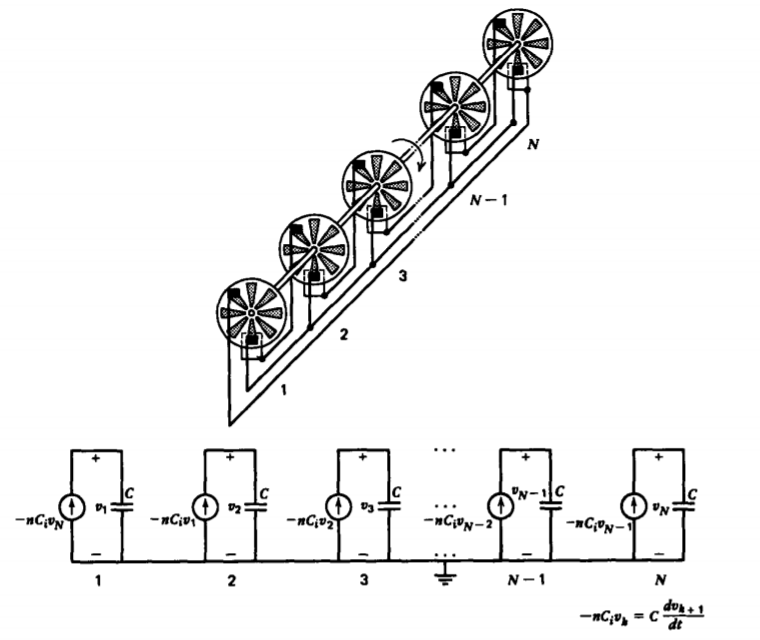
Si tenemos N tales generadores, como en la Figura 3-42, con el último conectado al primero, el k º circuito equivalente rinde

\[-nC_{i} \hat{\textrm{V}}_{k} = Cs \hat{\textrm{V}}_{k + 1} \nonumber \]

Esta es una ecuación lineal de diferencia de coeficiente constante. Análogamente a las soluciones exponenciales de tiempo en (3) válidas para ecuaciones diferenciales de coeficiente constante lineal, las soluciones a (10) son de la forma

\[\textrm{V}_{k} = A \lambda^{k} \nonumber \]

donde la raíz característica\(\lambda\) se encuentra por sustitución de nuevo en (10) para producir

\[-nC_{i}A \lambda^{k} = CsA \lambda^{k+1} \Rightarrow \lambda = - nC_{i}/Cs \nonumber \]

Figura 3-42 Máquina Wimshurst autoexcitada multifrecuencia polifásica con circuito equivalente.

Ya que el último generador está acoplado al primero, debemos tener ese

\[\textrm{V}_{N+1} = V_{1} \Rightarrow \lambda^{N+1} = \lambda^{1} \\ \Rightarrow \lambda^{N} = 1 \\ \lambda = 1^{1/N} = e^{j 2 wr/N}, \: \: \: \: \: r = 1,2,3,...,N \nonumber \]

donde nos damos cuenta de que la unidad tiene N raíces complejas.

Las frecuencias naturales del sistema se obtienen a partir de (12) y (13) como

\[s = - \frac{nC_{i}}{C \lambda} = - \frac{nC_{i}}{C} e^{-j2 \pi r/N}, \: \: \: \: r=1,2,...,N \nonumber \]

Vemos que para N = 2 y N = 3 recuperamos los resultados de (4) y (8). Todas las raíces con una parte real positiva de s son inestables y los voltajes se acumulan espontáneamente en el tiempo con frecuencias de oscilación\(\omega_{0}\) dadas por la parte imaginaria de s.

\[\omega_{0} = \vert \textrm{Im} (s) \vert = \frac{nC_{i}}{C} \vert \sin 2 \pi r/N \vert \nonumber \]