3.11: Problemas
- Page ID
- 86767
Sección 3-1
Un dipolo bidimensional está formado por dos cargas de línea paralela infinitamente largas de polaridad opuesta a\(\pm \lambda \) una pequeña\(d\textbf{i}_{y}\) distancia.
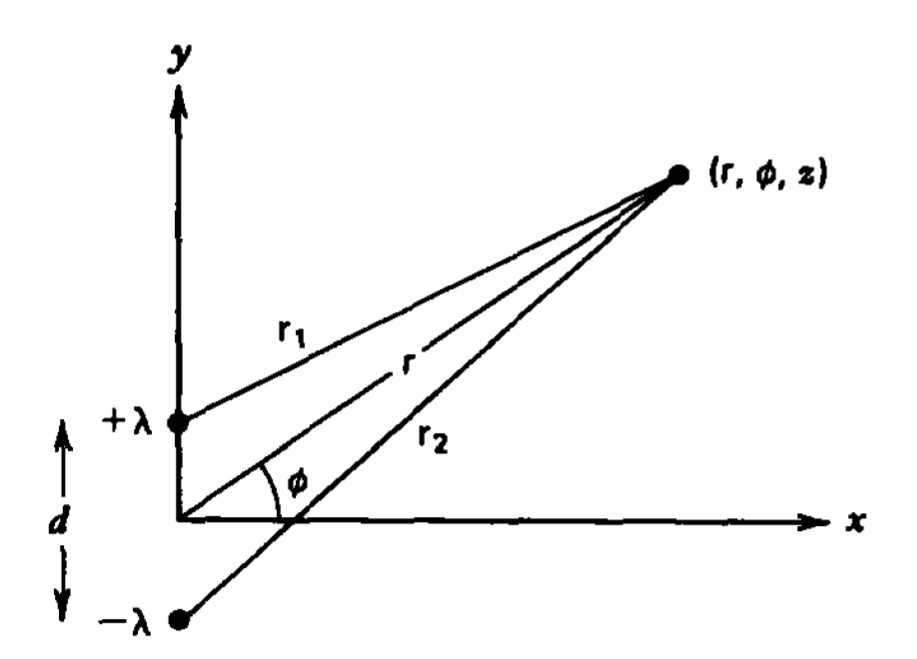
a) ¿Cuál es el potencial en cualquier coordenada\(\left ( \textrm{r},\phi ,z \right )\)?
b) ¿Cuál es el potencial y el campo eléctrico lejos del dipolo\(\left ( \textrm{r}\gg d \right )\)? ¿Cuál es el momento dipolar por unidad de longitud?
c) ¿Cuál es la ecuación de las líneas de campo?
Encuentre el momento dipolar para cada una de las siguientes distribuciones de carga:
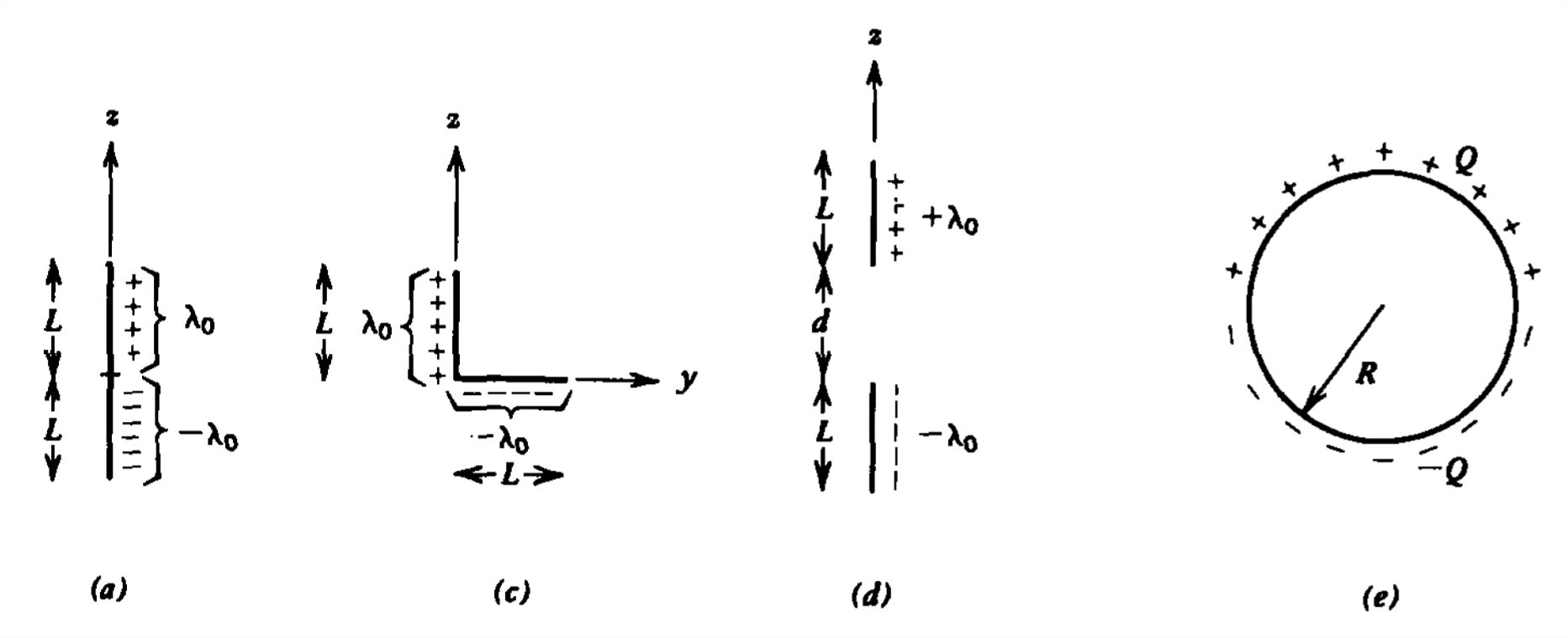
(a) Dos líneas colineales uniformes de polaridad opuesta se cargan\(\pm \lambda_{0}\) cada una a una pequeña distancia\(L\) a lo largo del\(z\) eje
b) Igual que (a) con la distribución de carga de línea como
\(\lambda(z) = \left \{ \begin{matrix} \lambda_{0}(1-z/L), & 0<z<L \\ - \lambda_{0}(1+ z/L), & -L <z <0 \end{matrix} \right.\)
c) Dos cargas uniformes de línea de polaridad opuesta\(\pm \lambda_{0}\) cada una de longitud\(L\) pero en ángulo recto.
d) Dos líneas paralelas, uniformes, de polaridad opuesta, cargan\(\pm \lambda_{0}\) cada una de longitud y\(L\) una\(d\textbf{i}_{z}\) distancia entre sí.
e) Una concha esférica con carga total distribuida uniformemente\(\mathcal{Q}\) en la mitad superior y\(-\mathcal{Q}\) en la mitad inferior. (Pista:\(\textbf{i}_{r}=\sin \theta \cos \phi \textbf{i}_{x}+\sin \theta \sin \phi \textbf{i}_{y}+\cos \phi \textbf{i}_{z}\).)
(f) Un volumen esférico con carga volumétrica total distribuida uniformemente\(\mathcal{Q}\) en la mitad superior y\(-\mathcal{Q}\) en la mitad inferior. (Pista: Integrar los resultados de (e).)
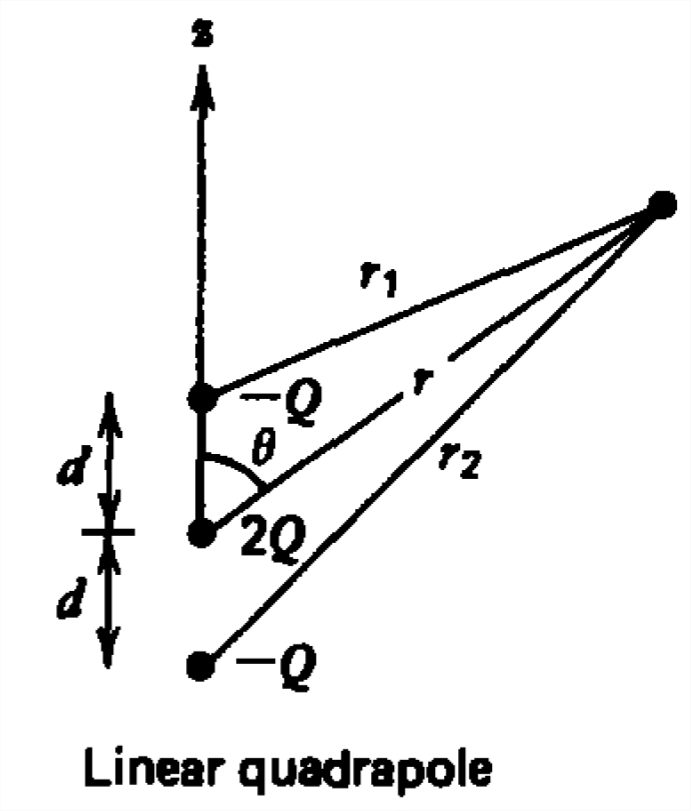
El cuadripolo lineal consta de dos dipolos superpuestos a lo largo del\(z\) eje. Encuentra el campo potencial y eléctrico para distancias alejadas de las cargas\(\left ( r\gg d \right )\).
Modele un átomo como un núcleo de carga positivo fijo\(\mathcal{Q}\) con una nube de electrones negativos esférica circundante de densidad de carga no uniforme:
\(\rho =-\rho _{0}\left ( 1-r/R_{0} \right ),\quad r< R_{0}\)
(a) Si el átomo es neutro, ¿qué es\(\rho _{0}\)?
b) Se aplica un campo eléctrico con campo local\(\textbf{E}_{\textrm{Loc}}\), provocando un ligero desplazamiento\(\textbf{d}\) entre el centro de la nube esférica y el núcleo positivo. ¿Cuál es el espaciamiento dipolar de equilibrio?
c) ¿Cuál es la polarizabilidad aproximada\(\alpha \) si\(9\varepsilon _{0}E_{\textrm{Loc}}/\left (\rho _{0}R_{0} \right )\ll 1 \)?
Dos dipolos colineales con polarizabilidad\(\alpha \) están\(a\) separados a lo largo del\(z\) eje. Se aplica un campo\(E_{0}\textbf{i}_{z}\) uniforme.
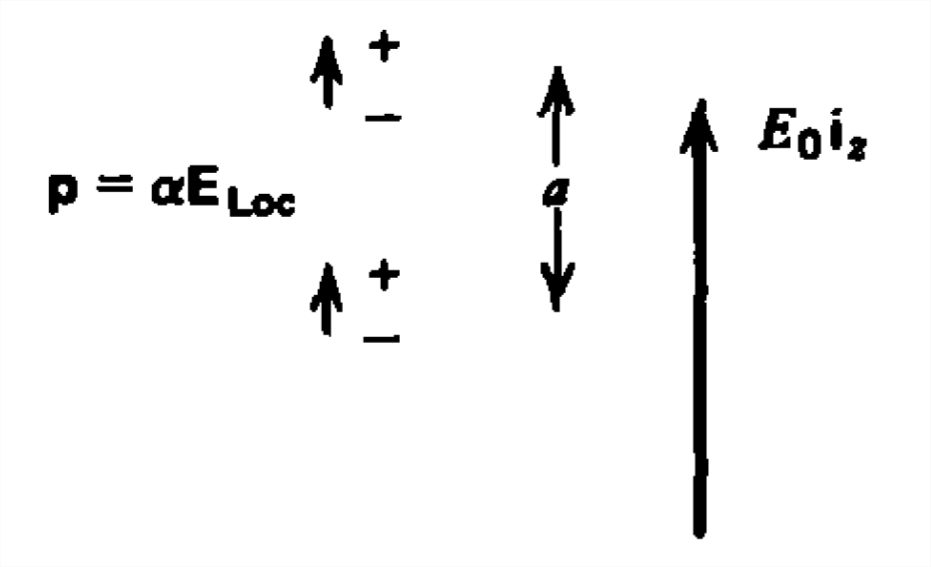
a) ¿Cuál es el campo local total visto por cada dipolo?
(b) Repetir (a) si tenemos una matriz infinita de dipolos con espaciado constante\(a\). (Pista:\(\sum_{n=1}^{\infty }1/n^{3}\approx 1.2\).)
(c) Si asumimos que tenemos uno de esos dipolos dentro de cada volumen de\(a^{3}\), ¿cuál es la permitividad del medio?
Un dipolo se modela como una carga puntual\(\mathcal{Q}\) rodeada por una nube esférica de electrones con radio\(R_{0}\). Entonces el campo local\(\textbf{E}_{\textrm{Loc}}\) difiere del campo aplicado\(\textbf{E}\) por el campo debido al propio dipolo. Dado que\(\textbf{E}_{\textrm{dip}}\) varía dentro de la nube esférica, utilizamos el campo promedio dentro de la esfera.
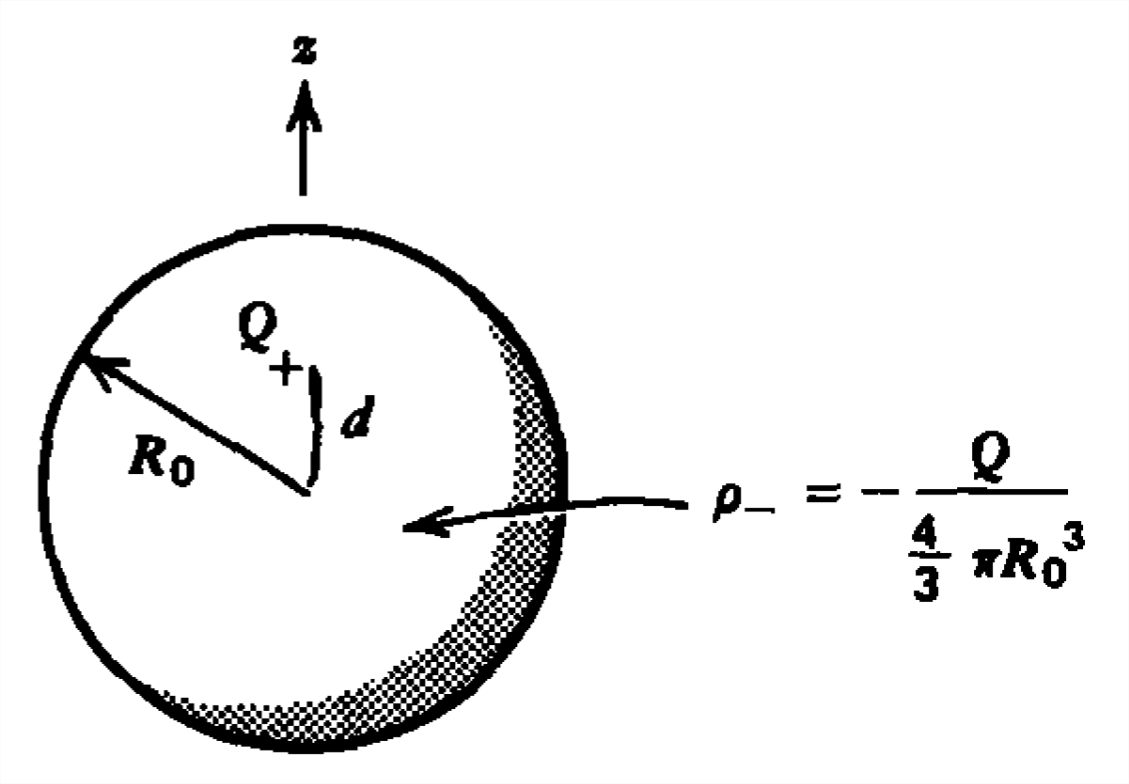
(a) Usando el centro de la nube como origen, mostrar que el campo eléctrico dipolo dentro de la nube es
\(\textbf{E}_{\textrm{dip}}=-\frac{\mathcal{Q}r\textbf{i}_{r}}{4\pi \varepsilon _{0}R_{0}^{3}}+\frac{\mathcal{Q}\left ( r\textbf{i}_{r}-d\textbf{i}_{z} \right )}{4\pi \varepsilon _{0}\left [ d^{2}+r^{2}-2rd\cos \theta \right ]^{3/2}}\)
(b) Demostrar que los componentes promedio\(x\) y de\(y\) campo son cero. (Pista:\(\textbf{i}_{r}=\sin \theta \cos \phi \textbf{i}_{x}+\sin \theta \sin \phi \textbf{i}_{y}+\cos \theta \textbf{i}_{z}\).)
c) ¿Cuál es el\(z\) componente promedio del campo? (Pista: Cambiar las variables a\(u=r^{2}+d^{2}-2rd\cos \theta \) y recordar\(\sqrt{\left ( r-d \right )^{2}}=\left | r-d \right |\).)
(d) Si tenemos un dipolo dentro de cada volumen de\(\frac{4}{3}\pi R_{0}^{3}\), ¿cómo se\(\textbf{P}\) relaciona la polarización con el campo aplicado\(\textbf{E}\)?
Supongamos que en el modelo dipolo de la Figura 3-5a la masa de la carga positiva es tan grande que solo la nube electoral se mueve como masa sólida\(m\).
a) El campo eléctrico local es\(\textbf{E}_0\). ¿Cuál es el espaciado dipolar?
(b) Al\(t = 0\), se apaga el campo local\(\left (\textbf{E}_{0}=0 \right )\). ¿Cuál es el movimiento posterior de la nube de electrones?
(c) ¿Cuál es la frecuencia de oscilación si\(\mathcal{Q}\) tiene la carga y la masa de un electrón con\(R_{0}=10^{-10}\,\textrm{m}\)?
(d) En un sistema real siempre hay alguna amortiguación que tomamos para ser proporcionales a la velocidad\(\left ( \textbf{f}_{\textrm{damping}} =-\beta \textbf{v} \right )\). ¿Cuál es la ecuación de movimiento de la nube de electrones para un campo eléctrico sinusoidal\(\textrm{Re}\left ( \hat{E}_{0}e^{j\omega t} \right )\)?
e) Escribir el desplazamiento impulsado del dipolo como
\(d=\textrm{Re}\left ( \hat{d}e^{j\omega t} \right ) \)
¿cuál es la polarizabilidad compleja\(\hat{\alpha }\), dónde\(\hat{p}=\mathcal{Q}\hat{d}=\hat{\alpha }E_{0}\)?
f) ¿Cuál es la constante dieléctrica compleja\(\hat{\varepsilon }=\varepsilon _{\textrm{r}}+j\varepsilon _{i}\) del sistema? (Pista: Definir\(\omega _{p}^{2}=\mathcal{Q}^{2}N/\left ( m\varepsilon _{0} \right )\).)
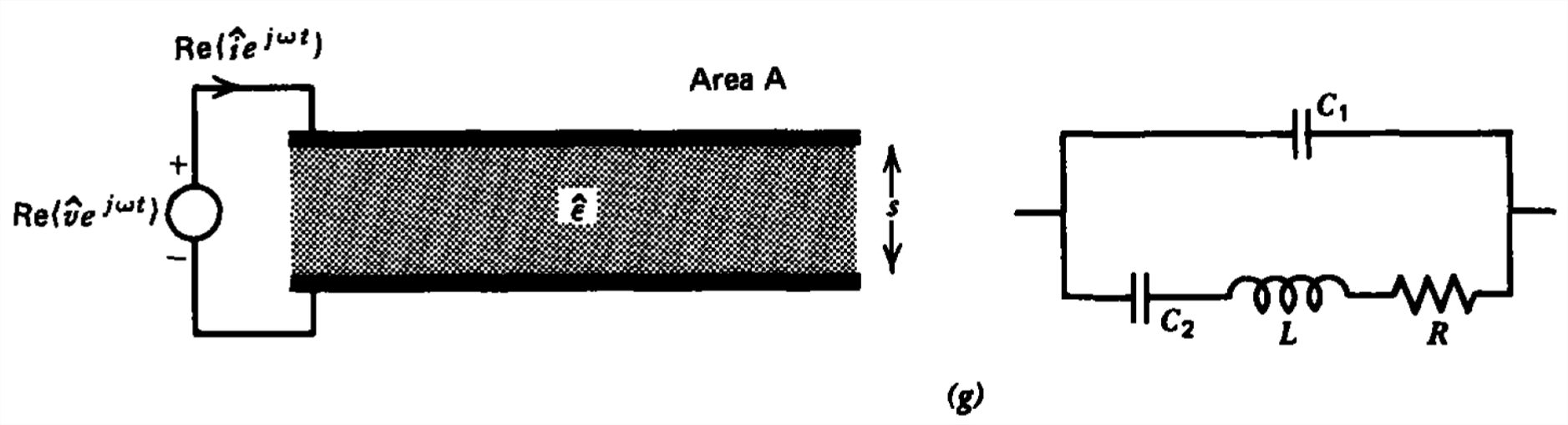
(g) Dicho dieléctrico se coloca entre electrodos de placa paralelos. Mostrar que el circuito equivalente es una serie\(R\)\(L\),\(C\), derivado por un condensador. ¿Qué son\(C_{1}\)\(C_{2}\),\(L\), y\(R\)?
(h) Considerar el límite donde la nube de electrones no tiene masa\((m = 0)\). Con la frecuencia\(\omega \) como parámetro muestran que una gráfica de\(\varepsilon _{r}\) versus como es un círculo. ¿Dónde está el centro del círculo y cuál es su radio? Tal diagrama se llama trama de Cole-Cole.
(i) ¿Cuál es el valor máximo de\(\varepsilon _{i}\) y con qué frecuencia ocurre?
Dos cargas puntuales de signo opuesto\(\pm \mathcal{Q}\) están a una distancia\(L\) por encima y por debajo del centro de una esfera conductora de radio conectada a tierra\(R\).
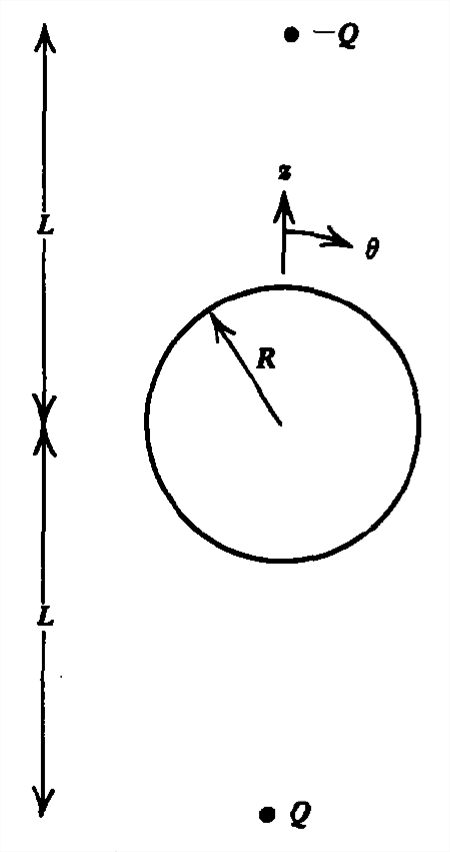
a) ¿Cuál es el campo eléctrico en todas partes a lo largo del\(z\) eje y en el\(\theta =\pi /2\) plano? (Pista: Usa el método de las imágenes.)
b) Deseamos que este problema modele el caso de una esfera conductora en un campo eléctrico uniforme llevando las cargas\(\pm \mathcal{Q}\) puntuales al infinito\(\left ( L\rightarrow \infty \right )\). ¿Cuál debe\(\mathcal{Q}/L^{2}\) ser tal la relación que el campo alejado de la esfera en el\(\theta =\pi /2\) plano sea\(E_{0}\textbf{i}_{z}\)?
c) En este límite, ¿cuál es el campo eléctrico en todas partes?
Un dipolo con momento\(\textbf{p}\) se coloca en un campo eléctrico no uniforme.
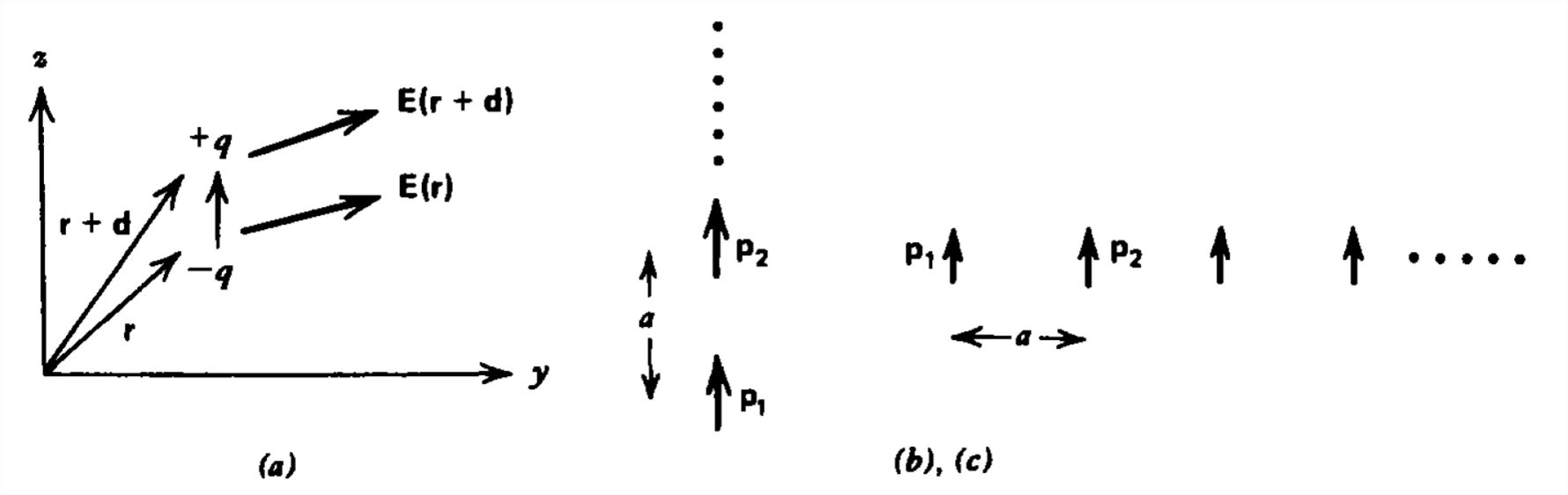
(a) Demostrar que la fuerza sobre un dipolo es
\(\textbf{f}=\left ( \textbf{p}\cdot \nabla \right )\textbf{E}\)
(b) Encontrar la fuerza sobre el dipolo\(1\) debida al dipolo\(2\) cuando los dos dipolos son colineales, o están adyacentes a una\(a\) distancia.
(c) Encontrar la fuerza sobre el dipolo\(1\) si es el último dipolo en una matriz infinita de dipolos colineales o adyacentes idénticos con espaciado\(a\). (Pista:\(\sum_{n=1}^{\infty }1/n^{4}=\pi ^{4}/90\).)
Un dipolo puntual con momento\(p\textbf{i}_{z}\) es una distancia\(D\) desde el centro de una esfera de radio conectada a tierra\(R\). (Pista:\(d\ll D\).)
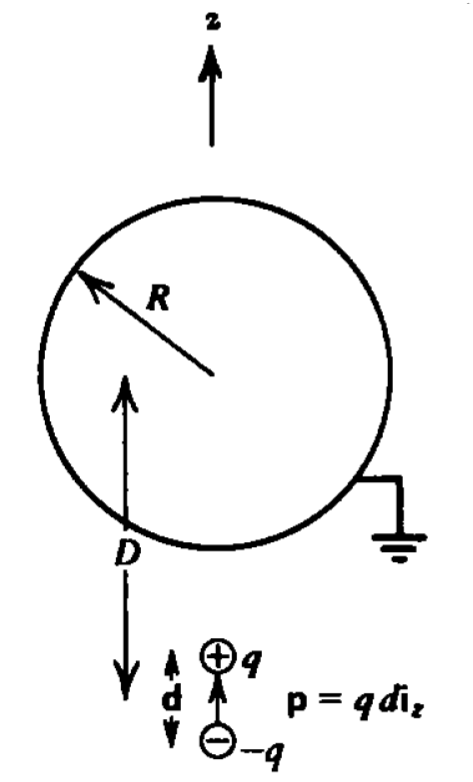
a) ¿Cuál es el momento dipolar inducido de la esfera?
b) ¿Cuál es el campo eléctrico en todas partes a lo largo del\(z\) eje?
c) ¿Cuál es la fuerza sobre la esfera? (Pista: Ver Problema 9a.)
Sección 3-2
Encuentre las distribuciones de potencial, campo eléctrico y densidad de carga para cada una de las siguientes cargas colocadas dentro de un medio de extensión infinita, descritas por conducción de deriva-difusión en el límite cuando el potencial eléctrico es mucho menor que el voltaje térmico\(\left ( qV/kT\ll 1 \right )\):
(a) Hoja de carga superficial o colocada en\(x =0\).
(b) Carga de línea infinitamente larga con densidad uniforme\(\lambda \). (Pista: resultados de la ecuación de Bessel.)
(c) Esfera conductora de radio\(R\) que lleva una carga superficial total\(\mathcal{Q}\).
Dos electrodos a potencial\(\pm V_{0}/2\) ubicados en\(x=\pm l\) encierran un medio descrito por conducción de deriva-difusión para dos portadores con carga opuesta, donde\(qV_{0}/kT\ll 1\).
(a) Encontrar las soluciones aproximadas de las distribuciones de potencial, campo eléctrico y densidad de carga. ¿Cuál es la polaridad de carga cerca de cada electrodo?
b) ¿Cuál es la carga total por unidad de área dentro del volumen del medio y en cada electrodo?
a) Despreciando los efectos de difusión pero incluyendo la inercia de carga y las colisiones, ¿cuál es la dependencia temporal de la velocidad de los portadores de carga cuando un campo\(E_{0}\textbf{i}_{x}\) eléctrico se enciende instantáneamente en\(t =0\)?
b) Después de que los portadores de carga hayan alcanzado su velocidad de estado estacionario, el campo eléctrico se apaga repentinamente. ¿Cuál es su velocidad resultante?
(c) Este material se coloca ahora entre electrodos de placa paralelos de área\(A\) y espaciamiento\(s\). Se aplica un voltaje sinusoidal\(\textrm{Re}\left ( V_{0}e^{j\omega t} \right ) \). ¿Cuál es el circuito equivalente?
Los electrodos de placa paralela encierran un superconductor que solo tiene electrones libres con frecuencia de plasma\(\omega _{pe}\).
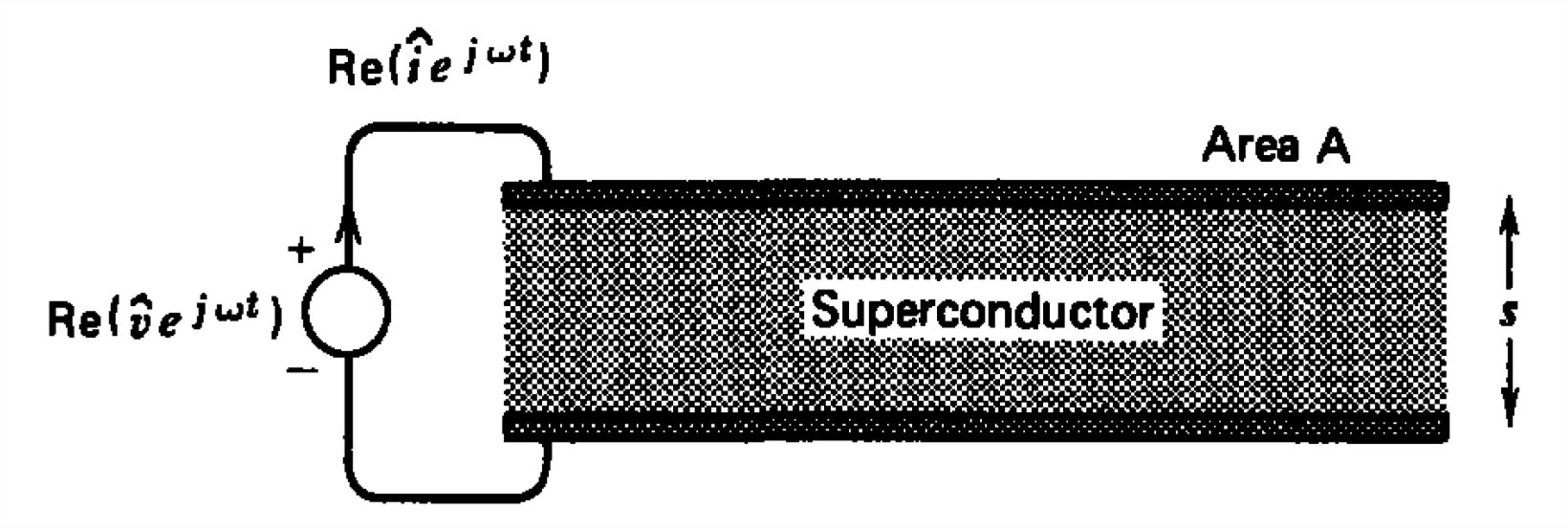
(a) ¿Cuál es la corriente del terminal cuando se aplica una tensión sinusoidal?
b) ¿Cuál es el circuito equivalente?
Un anillo conductor de radio\(R\) se gira a velocidad angular constante. El anillo tiene conductividad óhmica\(\sigma \) y área de sección transversal\(A\). Se conecta un galvanómetro a los extremos del anillo para indicar el paso de cualquier carga. La conexión se realiza mediante anillos deslizantes para que la rotación del anillo no se vea afectada por el galvanómetro. El anillo se detiene instantáneamente, pero los electrones dentro del anillo continúan moviéndose poco tiempo hasta que su impulso se disipa por colisiones. Para un electrón particular de carga\(q\) y\(m\) la conservación de masa del momento requiere
\(\Delta \left ( mu \right )=\int F\,dt\)
donde\(F=qE\) esta la fuerza sobre el electrón.
(a) Para el conductor óhmico, relacionar el campo eléctrico con la corriente en el cable.
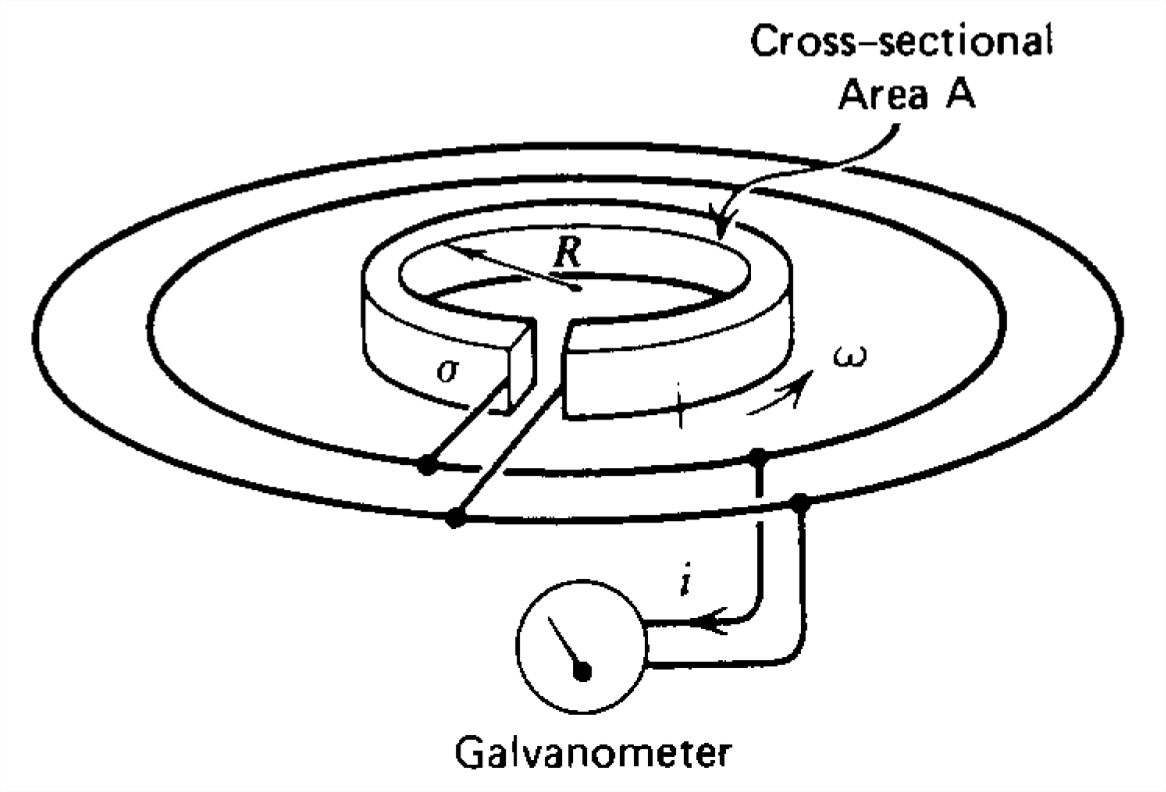
b) Cuando el anillo se detiene instantáneamente, ¿cuál es la carga\(\mathcal{Q}\) a través del galvanómetro? (Pista:\(\mathcal{Q}=\int i\,dt\). Este experimento es descrito por R. C. Tolman y T. D. Stewart, Phys. Rev. 8, No. 2 (1916), p.97.)
(c) Si el anillo es un superconductor de electrones con frecuencia de plasma\(\omega _{p}\), ¿cuál es la corriente resultante en el bucle cuando se detiene?
Sección 3.3
Un campo eléctrico con magnitud\(E_{1}\) incide sobre la interfaz entre dos materiales en ángulo con respecto\(\theta _{1}\) a la normal. Para cada una de las siguientes propiedades del material, encuentre la magnitud y dirección del campo\(\textbf{E}_{2}\) en la región\(2\).
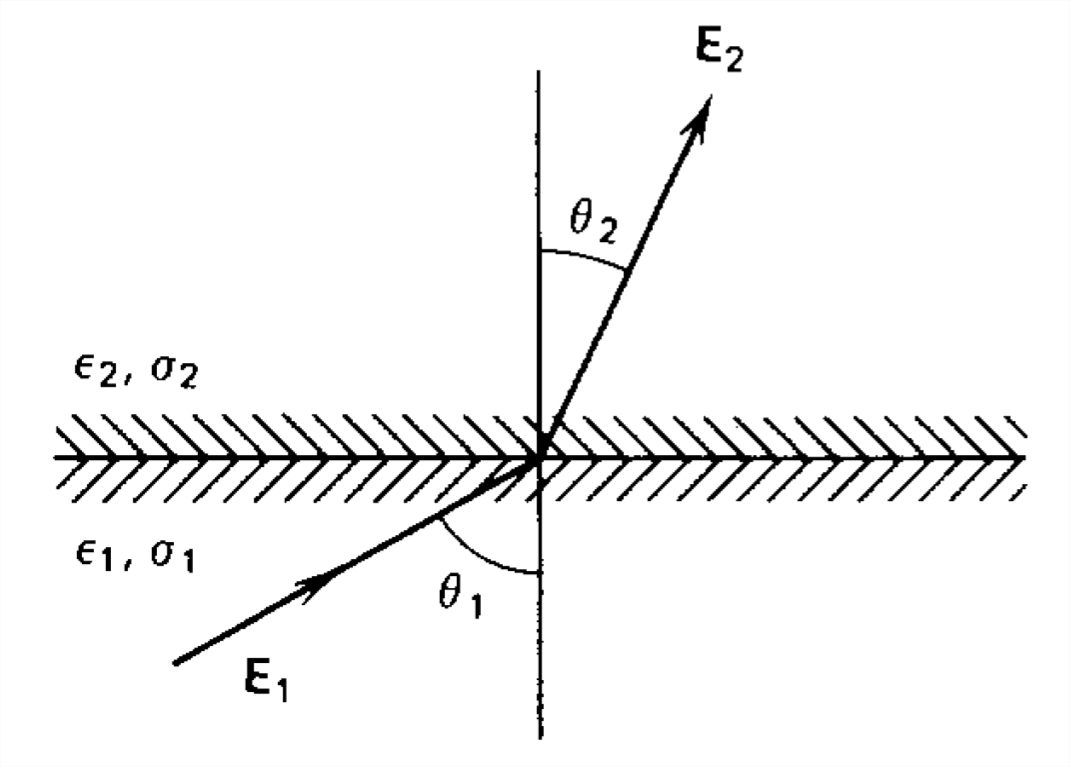
(a) Dieléctricos sin pérdidas con respectivas permitividades\(\varepsilon _{1}\) y\(\varepsilon _{2}\). No hay carga superficial interfacial.
(b) Materiales óhmicos con conductividades respectivas\(\sigma _{1}\) y\(\sigma _{2}\) en estado estacionario dc. ¿Cuál es la densidad de carga superficial libre\(\sigma _{f}\) en la interfaz?
(c) Dieléctricos con pérdida\(\left ( \varepsilon _{1},\sigma _{1} \right )\) y\(\left ( \varepsilon _{2},\sigma _{2} \right )\) con un campo eléctrico sinusoidalmente variable
\(E_{1}=\textrm{Re}\left ( \hat{E}_{1}e^{j\omega t} \right )\)
¿Cuál es la densidad de carga superficial libre\(\sigma _{f}\) en la interfaz?
Encuentre los campos eléctricos, de desplazamiento y de polarización y la carga de polarización en todas partes para cada una de las siguientes configuraciones:
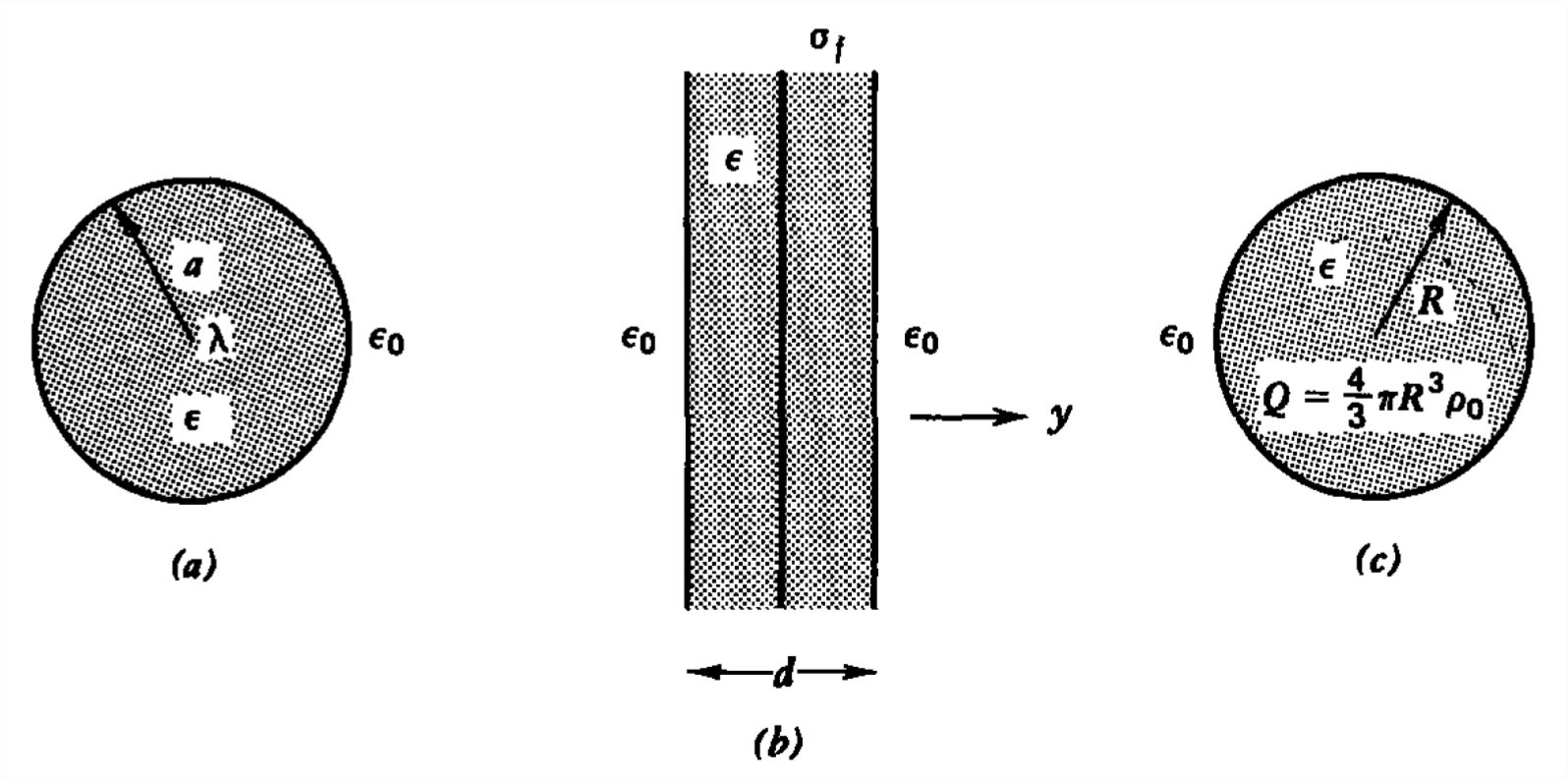
a) Una carga de línea infinitamente larga\(\lambda \) colocada en el centro de un cilindro dieléctrico de radio\(a\) y permitividad\(\varepsilon \).
b) Una lámina de carga superficial\(\sigma _{f}\) colocada en el centro de una losa dieléctrica con permitividad\(\varepsilon \) y grosor\(d\).
(c) Una esfera dieléctrica de carga uniforme con permitividad\(\varepsilon\) y radio\(R\) que transportan una carga total libre\(\mathcal{Q}\).
Lorentz calculó el campo local que actúa sobre un dipolo debido a un medio circundante polarizado uniformemente estresado por un campo\(E_{0}\textbf{i}_{z}\) macroscópico rodeando el dipolo con una pequeña cavidad esférica de espacio libre de radio\(R\).
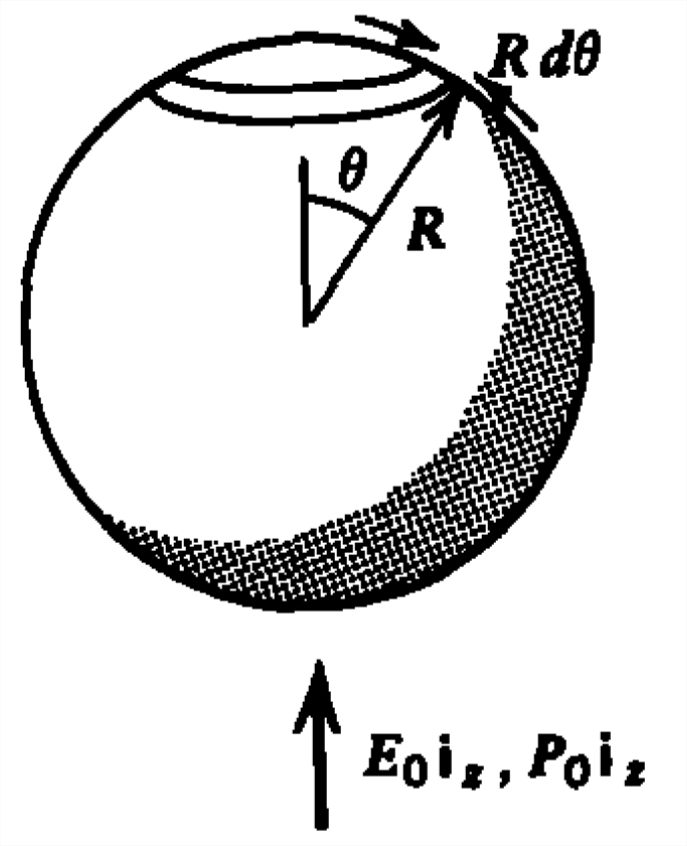
(a) Si el medio fuera de la cavidad tiene polarización\(P_{0}\textbf{i}_{z}\), ¿cuál es la carga de polarización superficial en la interfaz esférica? (Pista:\(\textbf{i}_{z}=\textbf{i}_{r}\cos \theta -\textbf{i}_{\theta }\sin \theta \))
(b) Romper esta distribución de carga de polarización superficial en elementos de carga de línea de aro de espesor\(d\theta \). ¿Cuál es la carga total en un proyectil en particular en ángulo\(\theta\)?
c) ¿Cuál es el campo eléctrico debido a esta concha en el centro de la esfera donde se encuentra el dipolo?
d) Al integrar sobre todas las conchas, encontrar el campo eléctrico total que actúa sobre el dipolo. A esto se le llama el campo Lorentz. (Pista: Vamos\(u=\cos \theta \)).
Una carga de línea\(\lambda \) dentro de un medio de permitividad\(\varepsilon _{1}\) está fuera de un cilindro dieléctrico de radio\(a\) y permitividad\(\varepsilon _{2}\). La carga de la línea es paralela al eje del cilindro y a una\(d\) distancia de éste.
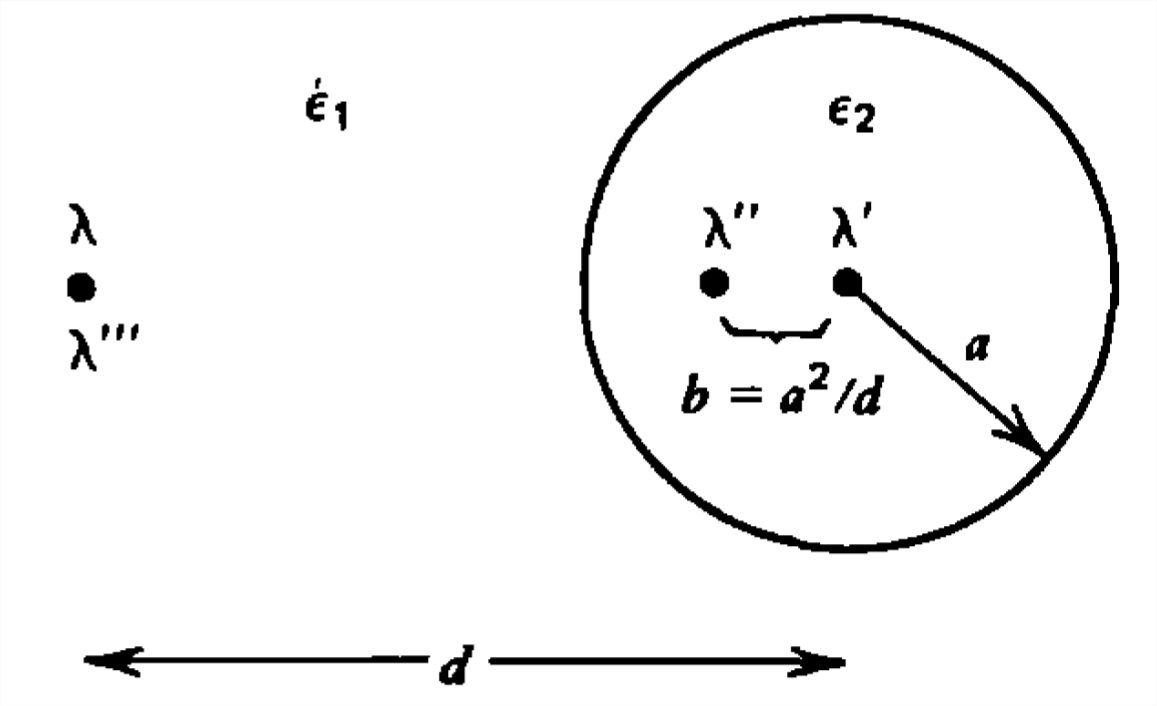
(a) Intente usar el método de imágenes colocando una carga de línea\(\lambda '\) en el centro y otra imagen\(\lambda ''\) dentro del cilindro a\(b=a^{2}/d\) distancia del eje a lo largo de la línea que une el eje a la carga de línea. Estas cargas de imagen junto con la carga de línea original determinarán el campo eléctrico fuera del cilindro. Ponga otra carga de línea\(\lambda '''\) en la posición de la carga de línea original para determinar el campo dentro del cilindro. ¿Qué valores de\(\lambda '\)\(\lambda ''\),, y\(\lambda '''\) satisfacer las condiciones límite?
(b) Verifique sus respuestas con la de la Sección 3-3-3 en el límite a medida que el radio del cilindro se hace grande para que parezca un avión.
c) ¿Cuál es la fuerza por unidad de longitud en la carga de la línea\(\lambda\)?
(d) Repita (a) - (c) cuando la carga de la línea\(\lambda\) esté dentro del cilindro dieléctrico.
Una carga puntual\(q\) es una distancia\(d\) por encima de un límite plano que separa dos materiales óhmicos con conductividades respectivas\(\sigma _{1}\) y\(\sigma _{2}\).
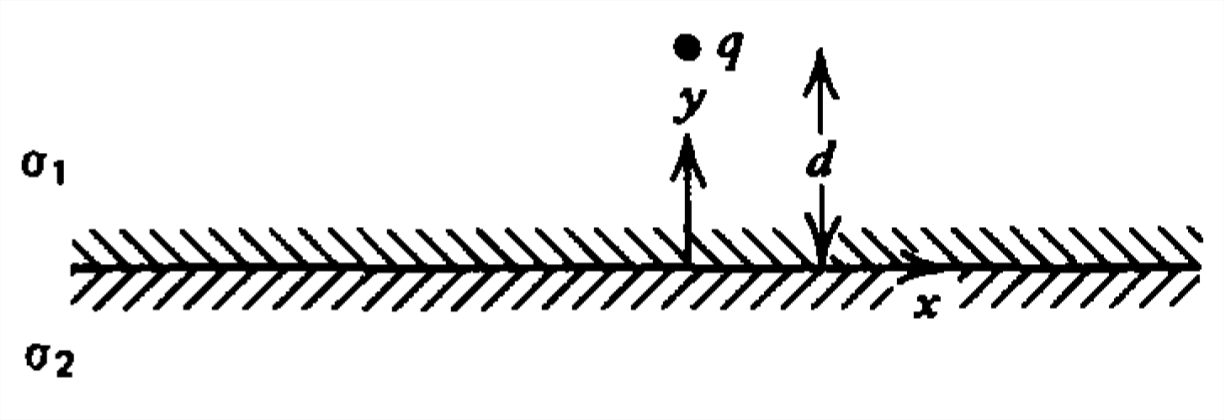
a) ¿Qué condiciones límite de estado estacionario debe satisfacer el campo eléctrico?
(b) ¿Qué configuración de carga de imagen satisfará estas condiciones de límite? (Pista: Ver Sección 3-3-3.)
c) ¿En qué consiste la fuerza\(q\)?
La polarización de un electreto se mide colocándolo entre electrodos de placa paralelos que se cortocircuitan entre sí.
(a) ¿Cuál es la carga superficial en el electrodo superior?
(b) Luego se abre el interruptor y el electrodo superior se aleja del electreto. ¿Qué voltaje se mide a través del condensador?
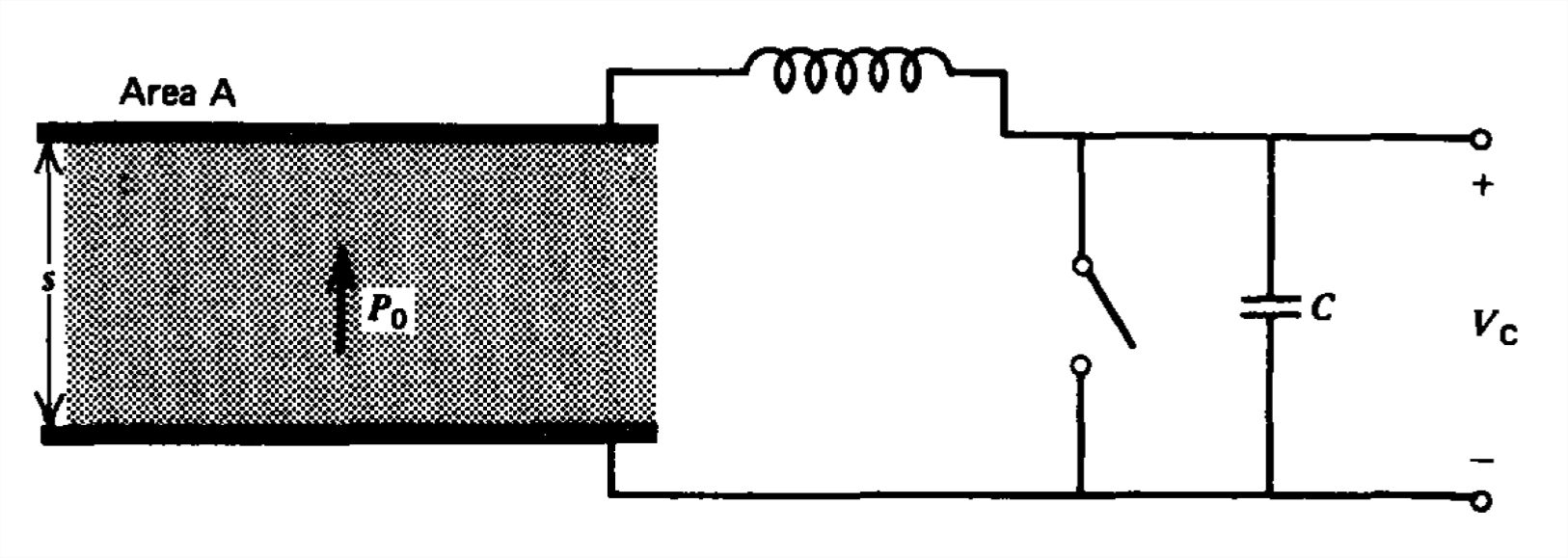
Un cilindro de radio\(a\) y altura\(L\) como en la Figura 3-14, tiene polarización
\(\textbf{P}=\frac{P_{0}z}{L}\textbf{i}_{z}\)
a) ¿Cuál es la distribución de carga de polarización?
b) Encontrar los campos eléctricos y de desplazamiento en todas partes a lo largo del\(z\) eje. (Pista: Utilice los resultados de las Secciones 2-3-5b y 2-3-5d.)
Encuentre el campo eléctrico en todas partes para las siguientes estructuras polarizadas permanentemente que no soportan ningún tipo de carga gratuita:
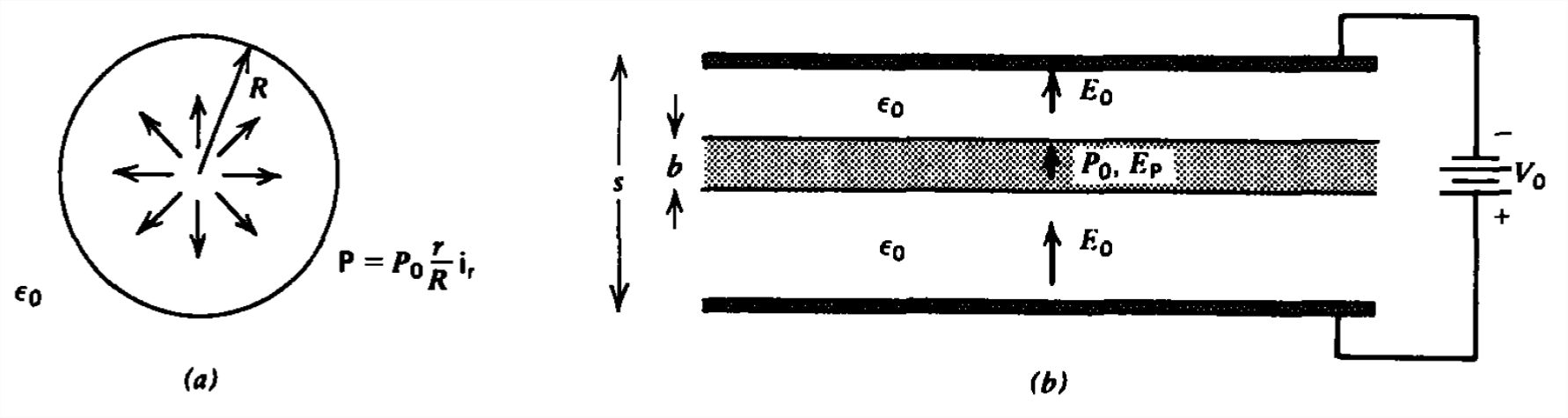
a) Esfera de radio\(R\) con polarización\(\textbf{P}=\left ( P_{0}r/R \right )\textbf{i}_{r}\).
(b) Losa permanentemente polarizada\( P_{0}\textbf{i}_{x}\) de espesor\(b\) colocada entre electrodos de placa paralela en espacio libre a diferencia de potencial\(V_0\).
Los electrodos de placa paralela encierran la combinación en serie de un conductor óhmico de espesor\(a\) con conductividad\(\sigma \) y un superconductor que solo tiene electrones libres con frecuencia de plasma\(\omega _{pe}\). Cuál es la dependencia temporal de la corriente del terminal, el campo eléctrico en cada región y la carga superficial en la interfaz que separa los dos conductores para cada una de las siguientes restricciones de terminal:
(a) Se aplica un voltaje\(V_0\) de paso a\(t=0\). ¿Para qué valores\(\omega _{pe}\) están los campos críticamente amortiguados?
(b) Se\(v\left ( t \right )=V_{0}\cos \omega t\) ha aplicado un voltaje sinusoidal durante mucho tiempo.
Sección 3-4
Encuentre la resistencia en serie y paralelo entre dos materiales con conductividades\(\sigma _{1}\) y\(\sigma _{2}\) para cada una de las siguientes geometrías de electrodos:
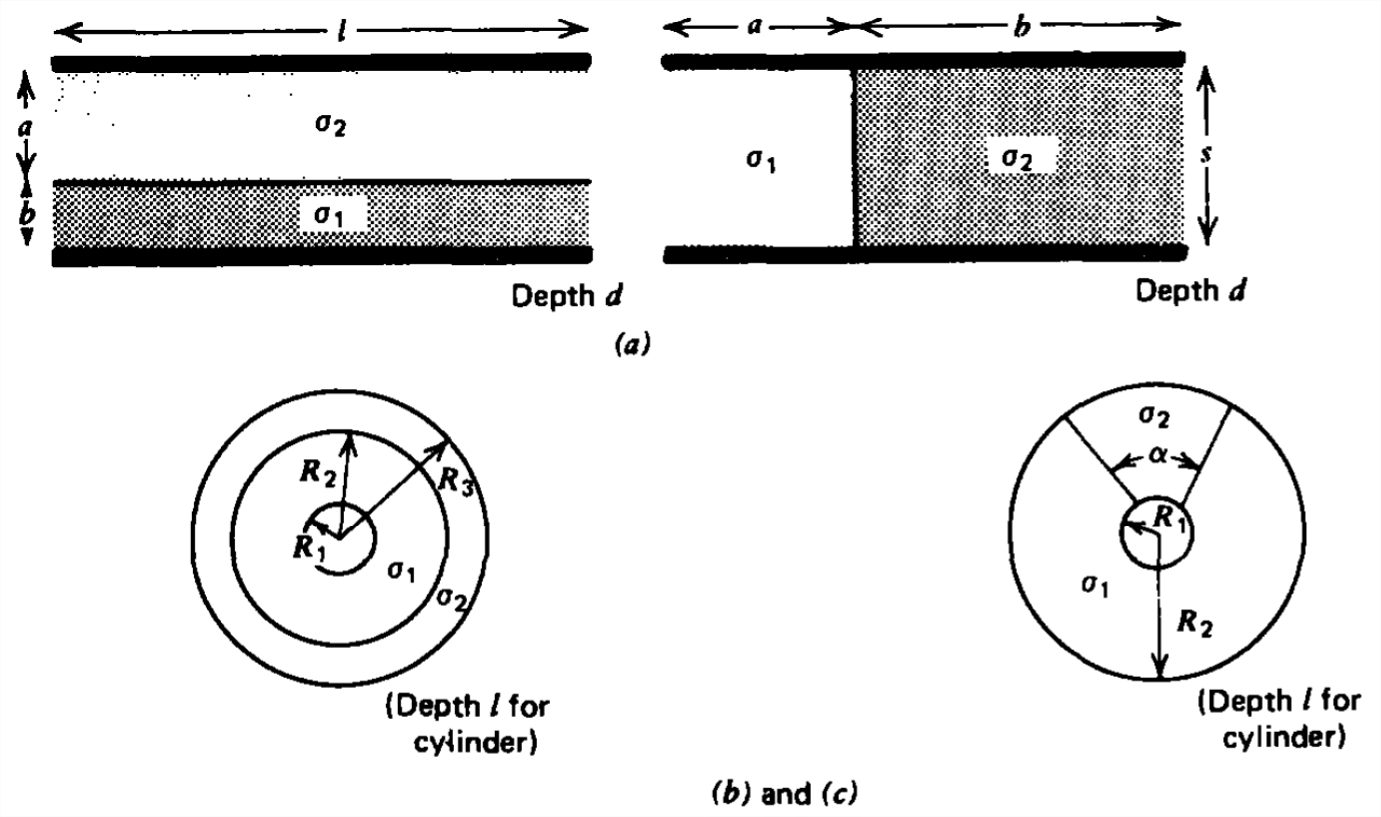
a) Placas paralelas.
(b) Cilindros coaxiales.
c) Esferas concéntricas.
Un par de electrodos de placa paralela a diferencia de voltaje\(V_{0}\) encierran un material óhmico cuya conductividad varía linealmente desde\(\sigma _{1}\) el electrodo\(\sigma _{2}\) inferior hasta el electrodo superior. La permitividad\(\epsilon \) del material es una constante.
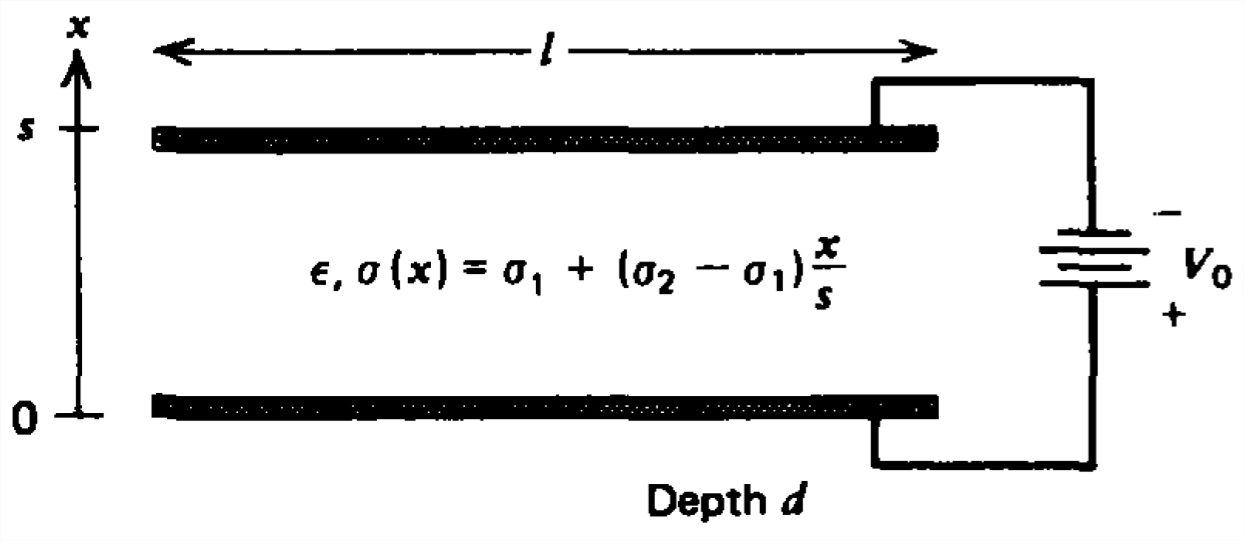
a) Encontrar los campos y la resistencia.
b) ¿Cuáles son las distribuciones de carga de volumen y superficie?
(c) ¿Cuál es la carga de volumen total en el sistema y cómo se relaciona con la carga superficial en los electrodos?
Un alambre de conductividad óhmica\(\sigma \) y área de sección transversal\(A\) se tuerce en las diversas formas mostradas. ¿Cuál es la resistencia\(R\) entre los puntos\(A\) y\(B\) para cada una de las configuraciones?
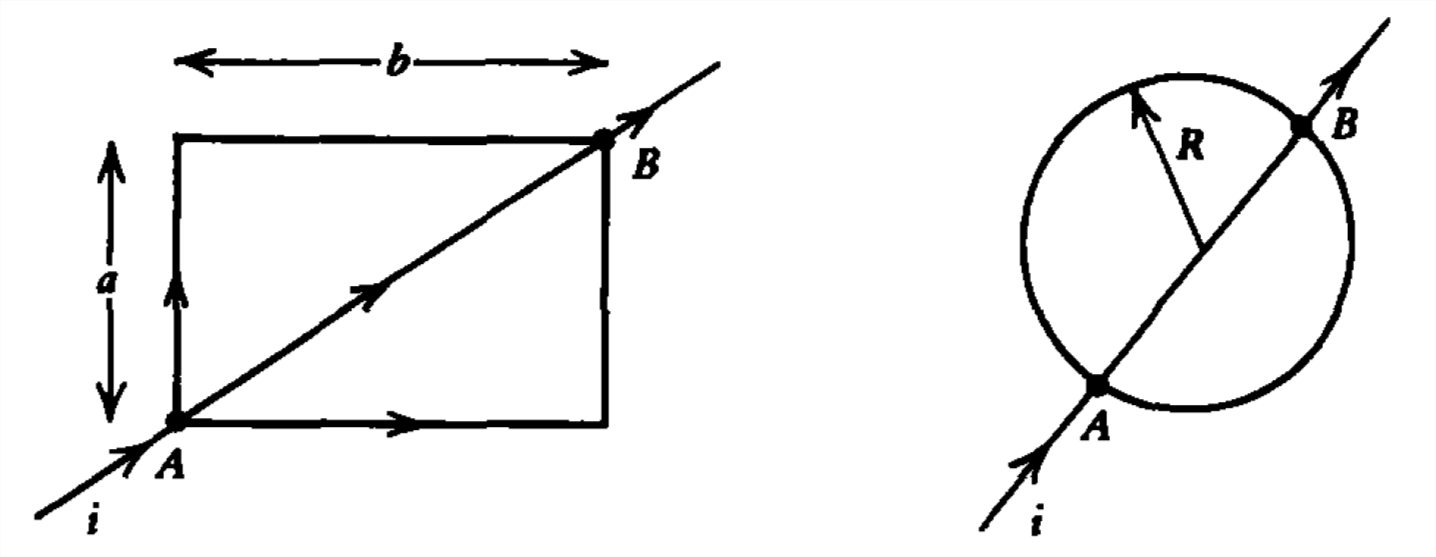
Sección 3-5
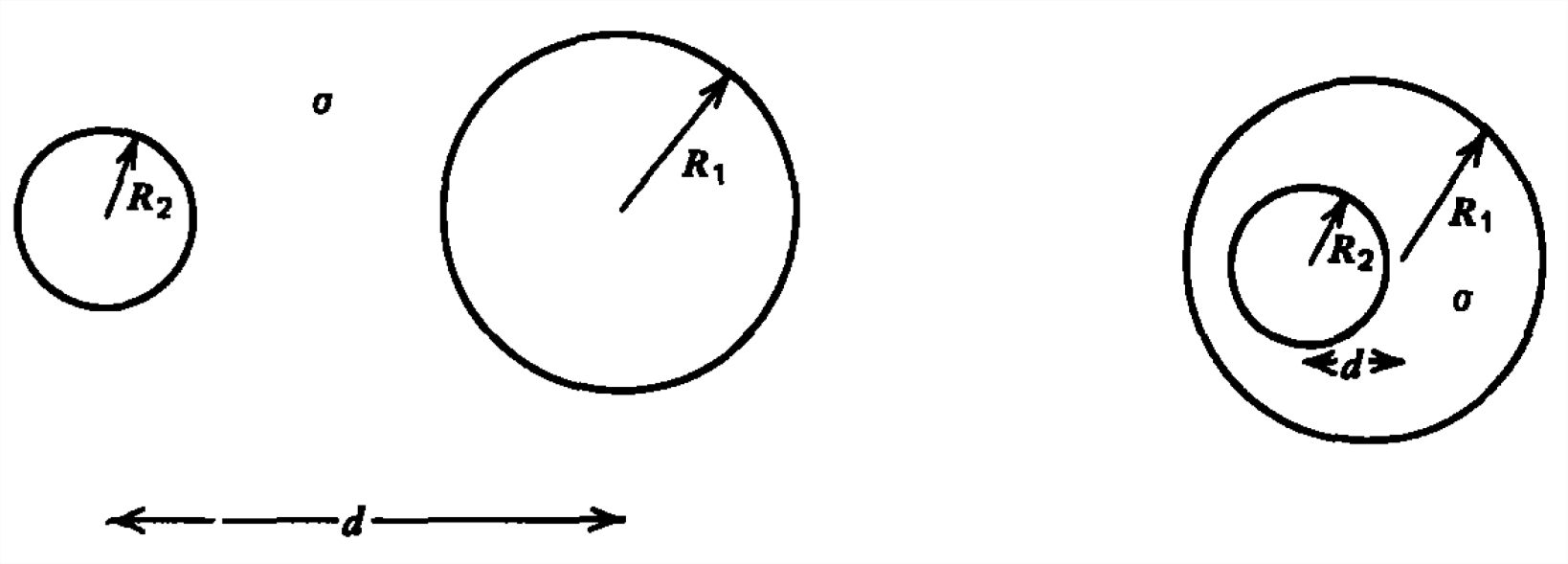
Dos cilindros conductores de longitud\(l\) y radios diferentes\(R_{1}\) y\(R_{2}\) dentro de un medio óhmico con conductividad\(\sigma \) tienen sus centros a\(d\) distancia. ¿Cuál es la resistencia entre los cilindros cuando están adyacentes y cuando el más pequeño está dentro del más grande? (Pista: Ver Sección 2-6-4c.)
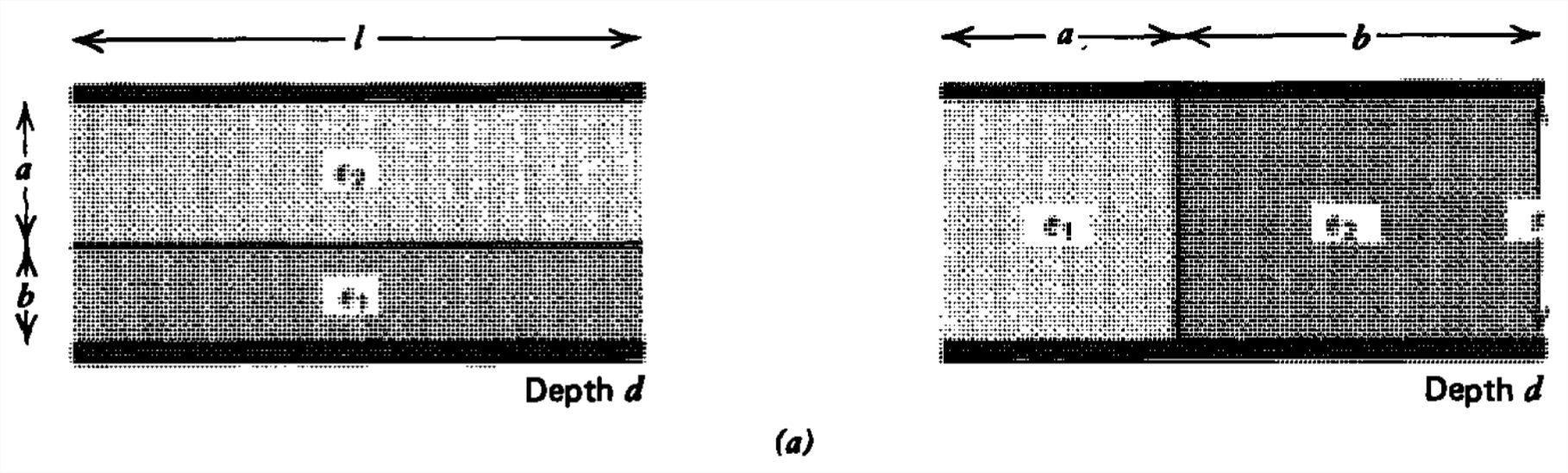
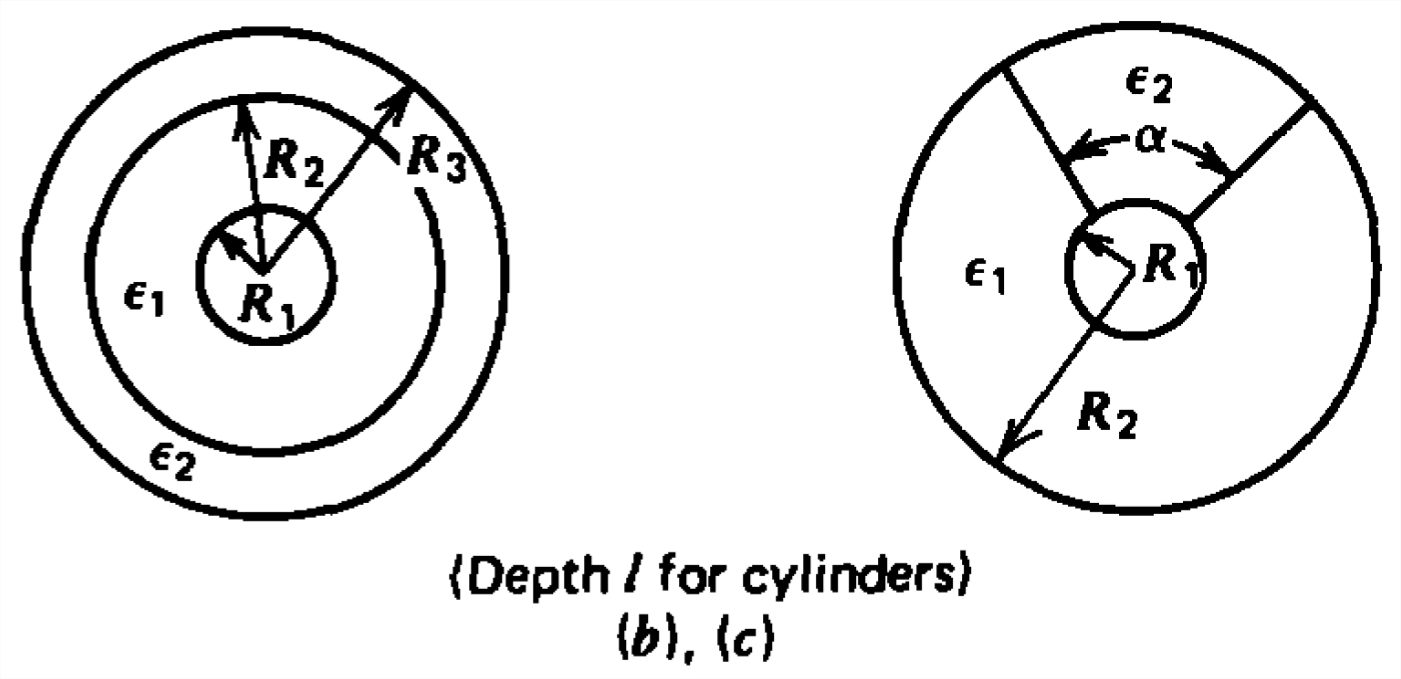
Encuentre la capacitancia en serie y paralelo para cada una de las siguientes geometrías:
a) Placa paralela.
(b) Cilindros coaxiales.
c) Esferas concéntricas.
Dos electrodos de forma arbitraria se colocan dentro de un medio de permitividad constante\(\varepsilon \) y conductividad óhmica\(\sigma \). Cuando\(V\) se aplica un voltaje de CC a través del sistema,\(I\) fluye una corriente.
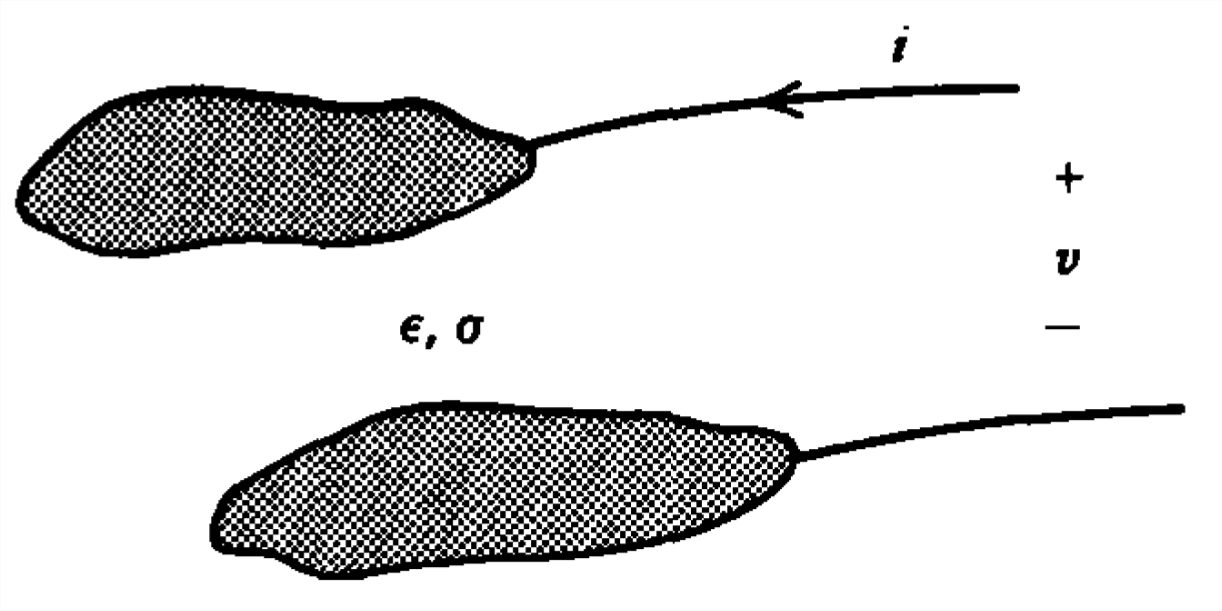
(a) ¿Cuál es la corriente\(i\left ( t \right )\) cuando\(\textrm{Re}\left ( V_{0}e^{j\omega t} \right )\) se aplica una tensión sinusoidal?
b) ¿Cuál es el circuito equivalente del sistema?
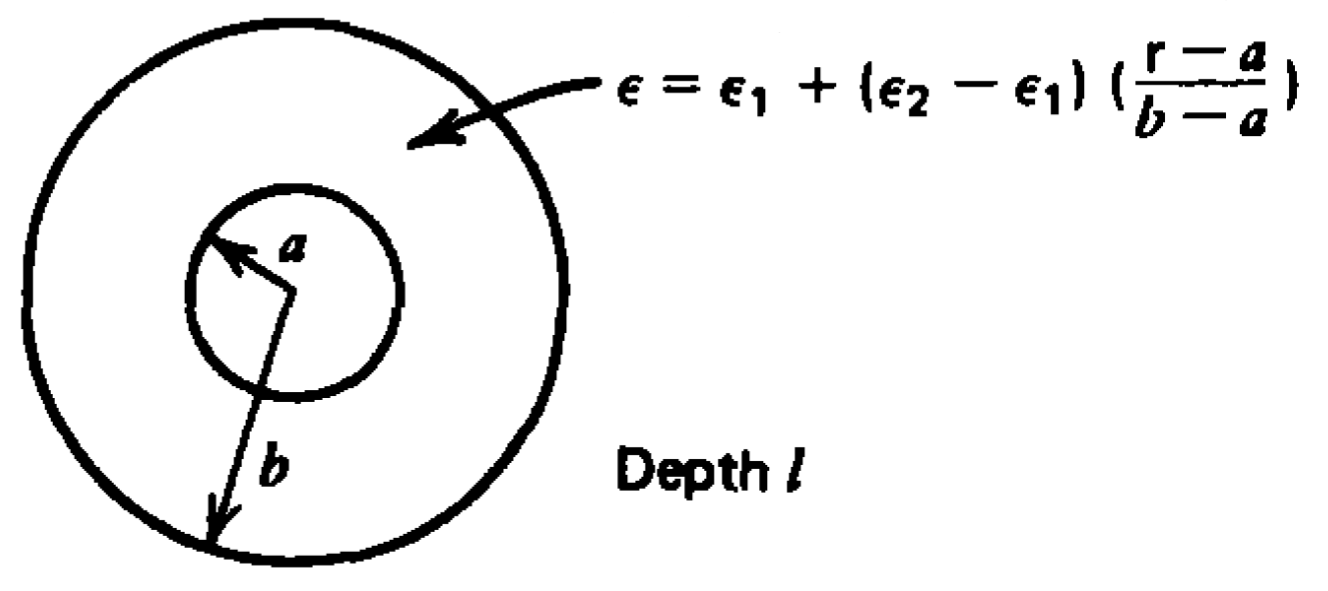
Electrodos cilíndricos concéntricos de longitud\(l\) con radios respectivos\(a\) y\(b\) encierran un material óhmico cuya permitividad varía linealmente con el radio desde\(\varepsilon _{1}\) el cilindro interno hasta\(\epsilon _{2}\) el exterior. ¿Cuál es la capacitancia? No hay carga de volumen en el dieléctrico.
Sección 3.6
Un material con pérdida con la permitividad\(\varepsilon _{0}\) de espacio libre y conductividad llena\(\sigma \) parcialmente la región entre electrodos de placa paralelos a diferencia de potencial constante\(V_{0}\) y se carga inicialmente uniformemente con densidad\(\rho _{0}\) a\(t =0\) con carga superficial cero en\(x=b\) . Cuál es la dependencia del tiempo de lo siguiente:
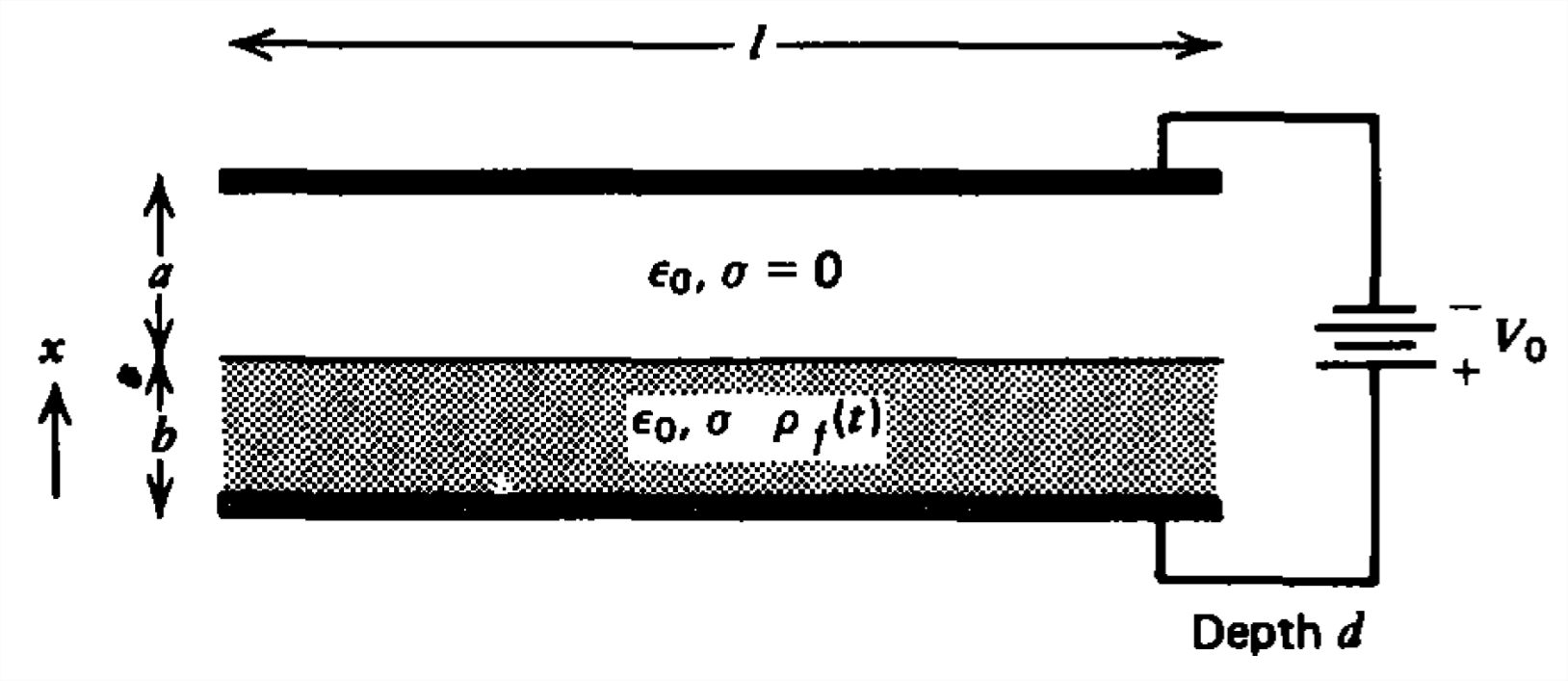
a) ¿El campo eléctrico en cada región? (Pista: Ver Sección 3-3-5.)
(b) la carga superficial a\(x=b\)?
c) ¿la fuerza sobre el material conductor?
Un cilindro infinitamente largo de radio\(a_{1}\), permitividad\(\varepsilon \) y conductividad no\(\sigma \) se carga uniformemente en\(t=0\):
\ (\ rho _ {f}\ izquierda (t=0\ derecha) =\ izquierda\ {\ begin {array} {ll}
\ rho _ {0}\ textrm {r} /a_ {0}, &\ quad 0<\ textrm {r} < a_ {0}\\
0, &\ quad\ textrm {r} > a_ {0}
\ end {array}\ derecho. \)
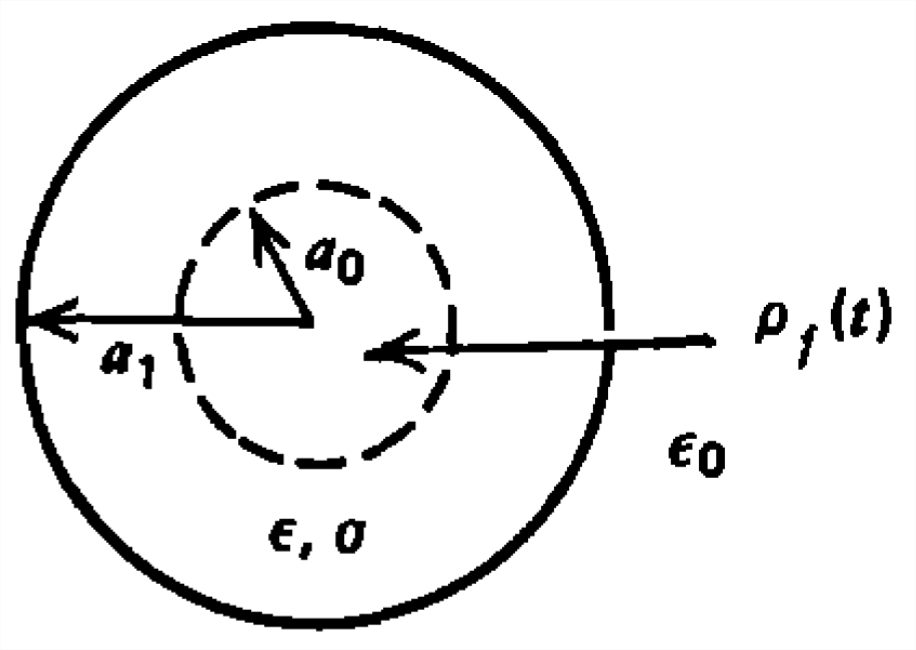
¿Cuál es la dependencia del tiempo del campo eléctrico en todas partes y la carga superficial en\(\textrm{r}=a_{1}\)?
Los electrodos cilíndricos concéntricos encierran dos medios diferentes en serie. Encuentre el campo eléctrico, la densidad de corriente y las cargas superficiales en todas partes para cada una de las siguientes condiciones:
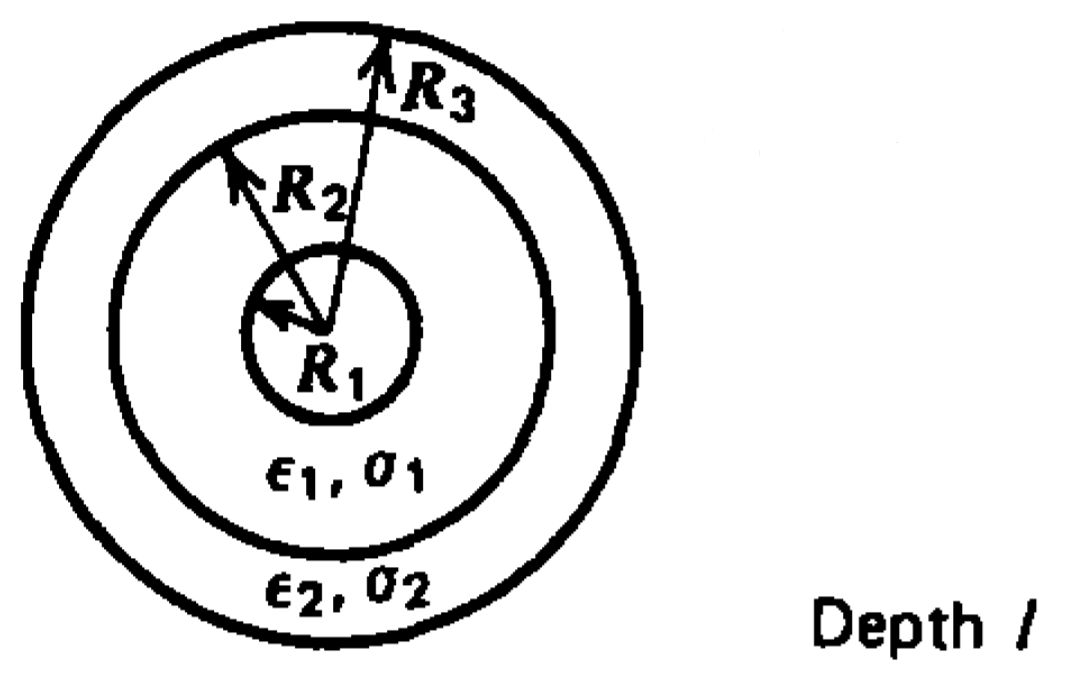
a)\(t=0_{+}\) inmediatamente después de aplicar una tensión\(V_{0}\) escalonada al sistema inicialmente no excitado;
b)\(t= \infty \) cuando los campos hayan alcanzado sus valores de estado estacionario dc;
(c) durante el intervalo transitorio intermedio. (¿Cuál es la constante de tiempo\(\tau \)?) ;
d)\(V_{0}\cos \omega t\) se aplique una tensión sinusoidal que haya estado encendida desde hace mucho tiempo;
e) ¿Cuál es el circuito equivalente para este sistema?
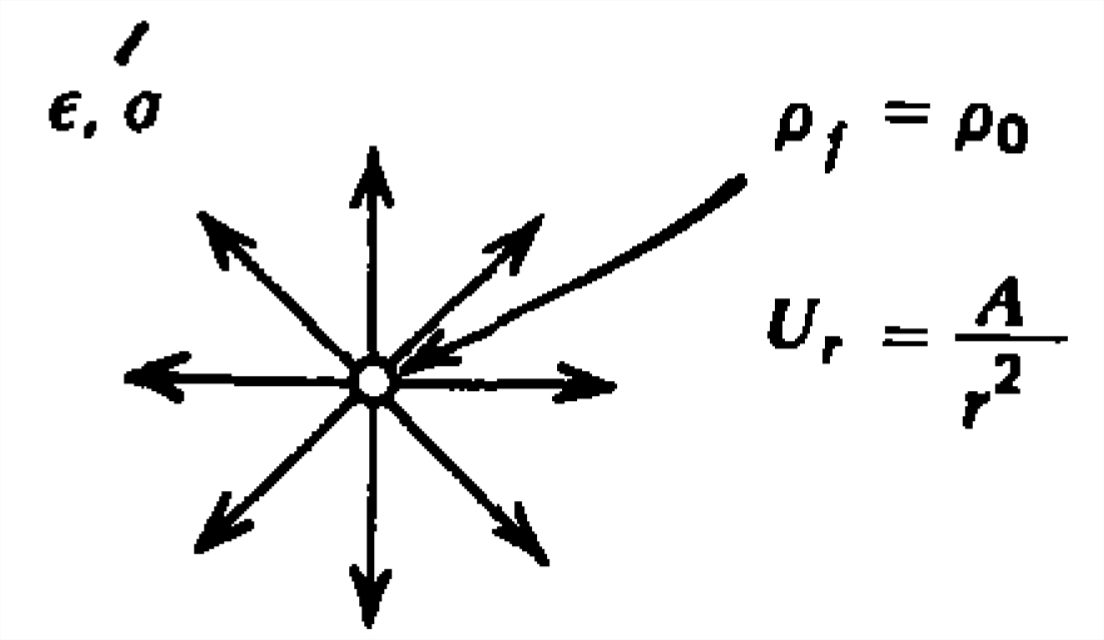
Un flujo de fluido emana radialmente desde una salida puntual con distribución de velocidad\(U_{r}=A/r^{2}\). El fluido tiene conductividad óhmica\(\sigma \) y permitividad\(\varepsilon\). Una fuente externa mantiene la densidad de carga\(\rho _{0} \) en\(r=0\). ¿Cuáles son las distribuciones de carga y campo eléctrico en estado estacionario en todo el espacio?
La carga mantenida\(\rho _{0} \) a densidad constante\(x=0\) es arrastrada por un fluido conductor que viaja a velocidad constante\(U\textbf{i}_{x}\) y se recoge a\(x=l\).
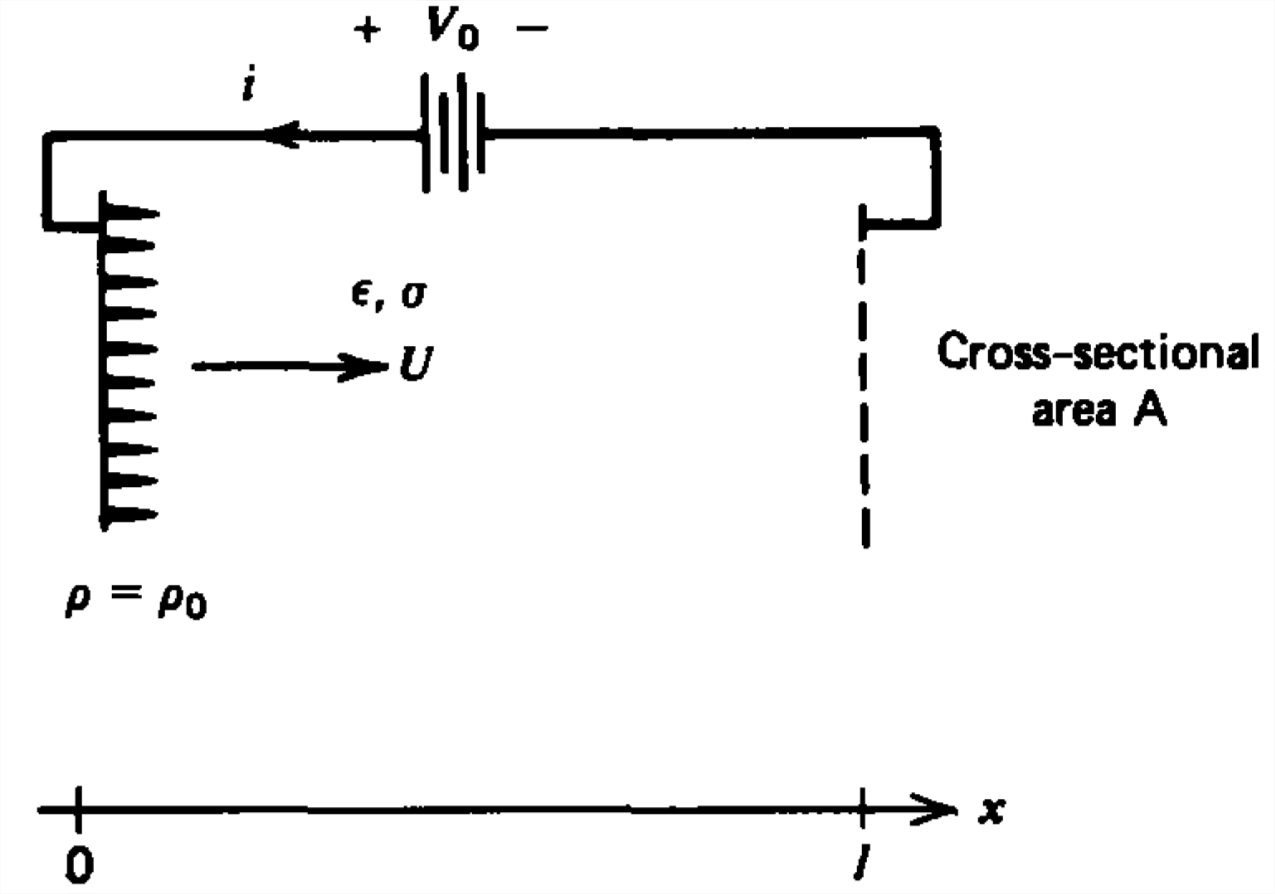
(a) ¿Cuáles son las distribuciones de campo y carga dentro del fluido si los electrodos están en diferencia de potencial\(V_{0}\)?
b) ¿Cuál es la fuerza sobre el fluido?
(c) Repita (a) y (b) si la fuente de voltaje es reemplazada por una resistencia de carga\(R_{L}\).
Un voltaje de CC se ha aplicado durante mucho tiempo a una estructura resistivo-capacitiva de circuito abierto para que el voltaje y la corriente tengan sus distribuciones de estado estacionario según lo dado por (44). Encuentre los transitorios de descarga resultantes para voltaje y corriente si en\(t = 0\) los terminales en\(z = 0\) son repentinamente:
(a) circuito abierto. Insinuación:
\(\int_{0}^{l}\sinh a\left ( z-l \right )\sin \left ( \frac{m\pi z}{l} \right )dz=-\frac{m\pi }{l}\frac{\sinh al}{\left [ a^{2}+\left ( m\pi /l \right )^{2} \right ]}\)
b) Cortocircuito. Pista:
\(\int_{0}^{l}\cosh a\left ( z-l \right )\sin \left ( \frac{\left ( 2n+1 \right )\pi z}{2l} \right )\textrm{dz}=\frac{\left ( 2n+1 \right )\pi \cosh al}{2l\left [ a^{2}+\left [ \frac{\left ( 2n+1 \right )\pi }{2l} \right ]^{2} \right ]}\)
En\(t =0\) una línea resistiva distribuida como se describe en la Sección 3-6-4 tiene un voltaje dc de paso\(V_{0}\) aplicado a\(z =0\). El otro extremo en\(z=l\) está cortocircuitado.
a) ¿Cuáles son las distribuciones de voltaje y corriente en estado estacionario?
b) ¿Cuál es la dependencia temporal de la tensión y la corriente durante el intervalo transitorio? Pista:
\(\int_{0}^{l}\sinh a\left ( z-l \right )\sin \left ( \frac{m\pi z}{l} \right )dz=-\frac{m\pi \sinh al}{l\left [ a^{2}+\left ( m\pi /l \right )^{2} \right ]}\)
Una línea resistiva distribuida se excita\(z = 0\) con una fuente de voltaje sinusoidal\(v\left ( t \right )=V_{0}\cos \omega t\) que ha estado encendida durante mucho tiempo. El otro extremo en\(z=l\) está abierto o cortocircuitado.
a) Uso de notación fasora compleja de la forma
\(v\left ( z,t \right )=\textrm{Re}\left ( \hat{v}\left ( z \right )e^{j\omega t} \right )\)
encontrar las distribuciones sinusoidales de voltaje y corriente de estado estacionario para cada terminación.
b) ¿Cuáles son las frecuencias naturales complejas del sistema?
c) ¿Cuánto tiempo la potencia promedio es entregada por la fuente?
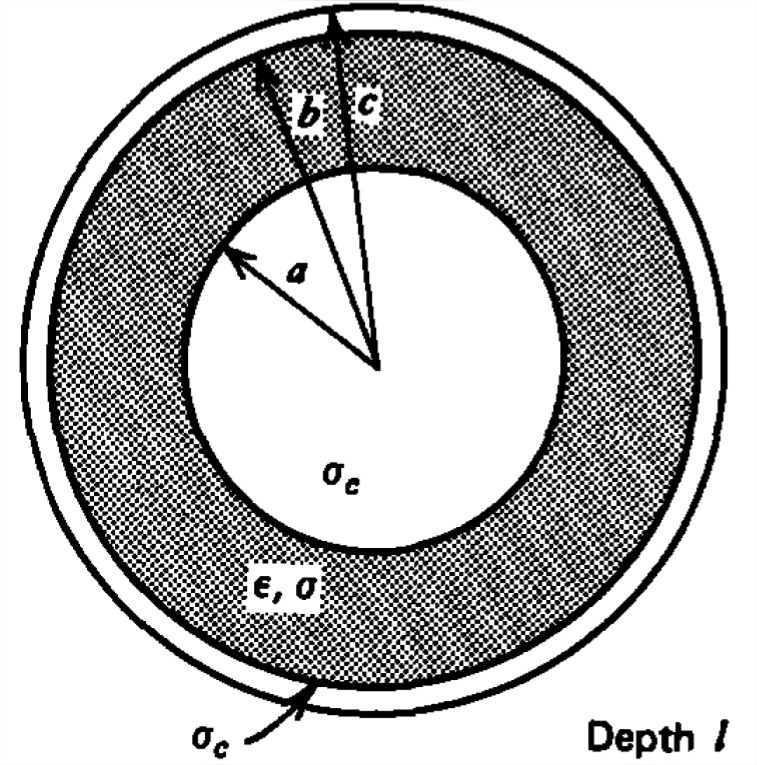
Se coloca un dieléctrico con pérdida con permitividad\(\varepsilon \) y conductividad\(\sigma \) óhmica entre electrodos cilíndricos coaxiales con gran conductividad\(\sigma _c\) y longitud óhmica\(l\).
¿Cuál es la resistencia en serie por unidad\(2R\) de longitud de los electrodos, y la capacitancia\(C\) y conductancia\(G\) por unidad de longitud del dieléctrico?
Sección 3.7
Dos electrodos de placa paralela de espaciamiento que\(l\) encierran un dieléctrico con permitividad\(\varepsilon \) son estresados por un voltaje escalonado en\(t =0\). Luego se inyecta carga positiva\(t =0\) desde el electrodo inferior con movilidad\(\mu \) y se desplaza hacia el electrodo opuesto.
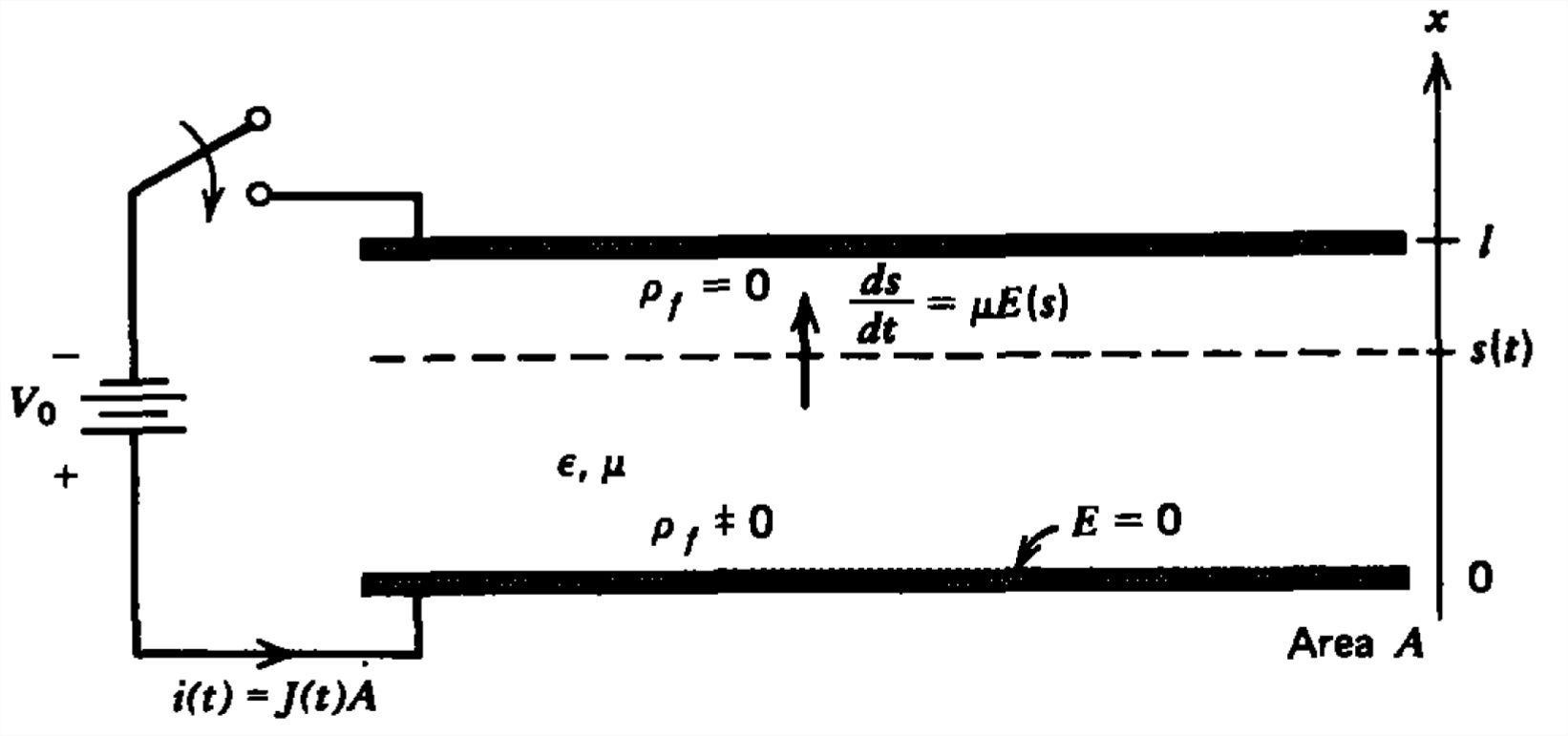
(a) Usando la ecuación de conservación de carga de la Sección 3-2-1, mostrar que la ecuación gobernante es
\(\frac{\partial E}{\partial t}+\mu E\frac{\partial E}{\partial x}=\frac{J\left ( t \right )}{\varepsilon }\)
donde\(J\left ( t \right )\) es la corriente por unidad de área de electrodo a través de los cables terminales. Esta corriente no depende de\(x\).
(b) Al integrar (a) entre los electrodos, relacionar la corriente\(J\left ( t \right )\) únicamente con el voltaje y el campo eléctrico en los dos electrodos.
(c) Para condiciones limitadas de carga espacial\((E(x = 0) = 0)\), encuentre la dependencia temporal del campo eléctrico en el otro electrodo\(E\left ( x=l,t \right )\) antes de que el frente de carga lo alcance. (Pista: Con voltaje constante,\(J\left ( t \right )\) de (b) solo depende de\(E\left ( x=l,t \right )\). Usando (a) en\(x=l\) sin cargo,\(\partial E/\partial x=0\), tenemos una única ecuación diferencial en\(E\left ( x=l,t \right )\).)
d) ¿Cuál es el campo eléctrico que actúa sobre el frente de carga? (Pista: No hay cargo por delante del frente.)
e) ¿Cuál es la posición del frente\(s(t)\) en función del tiempo?
(f) ¿A qué hora llega el frente al otro electrodo?
g) ¿Cuál es la distribución en estado estacionario del potencial, el campo eléctrico y la densidad de carga? ¿Cuál es la densidad de corriente en estado estacionario\(J\left ( t\rightarrow \infty \right )\)?
(h) Repita (g) para condiciones limitadas de carga no espacial cuando el campo eléctrico del emisor\((E(x = 0) = E_{0})\) sea distinto de cero.
En una geometría cilíndrica coaxial de longitud\(L\), el electrodo interno\(r=R_{i}\) es una fuente de iones positivos con movilidad\(\mu \) en el medio dieléctrico. El cilindro interior está a una tensión de CC\(V_{0}\) con respecto al cilindro exterior.
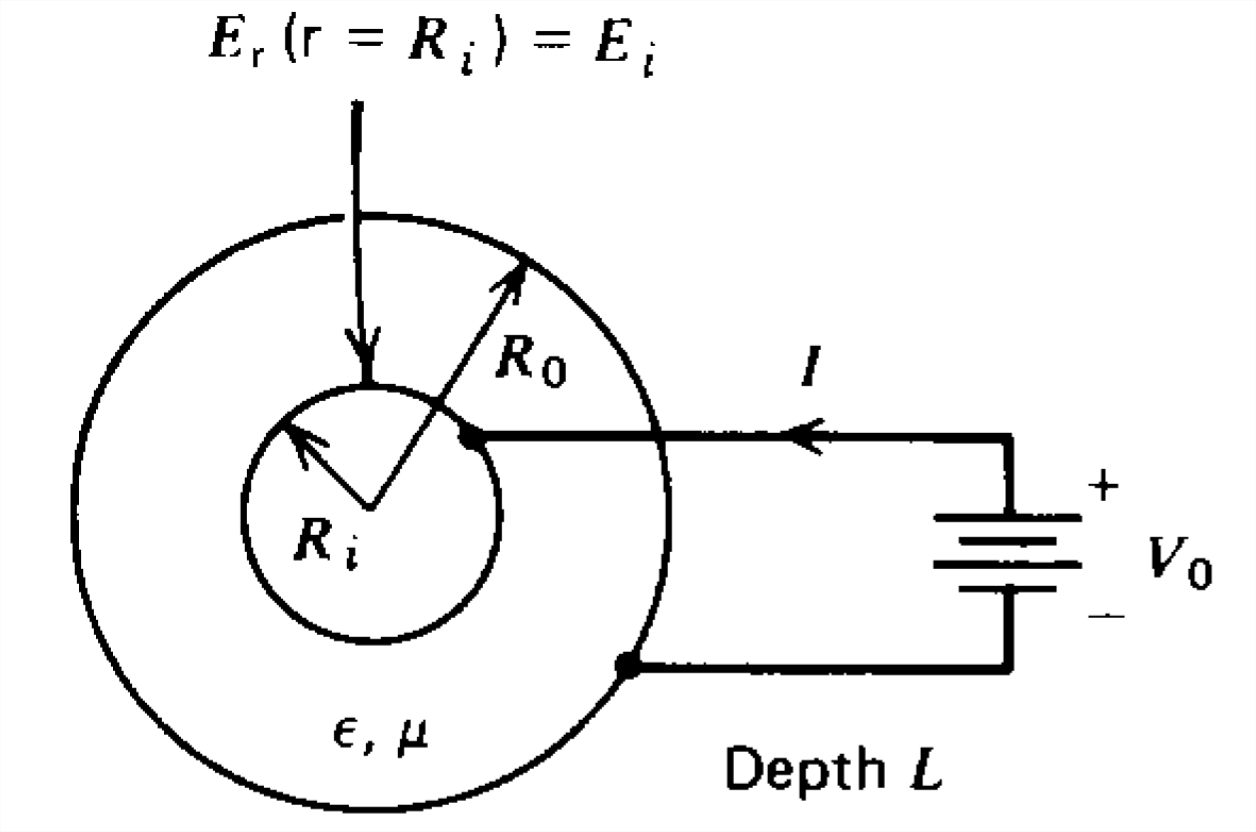
(a) El campo eléctrico en el electrodo emisor se da como\(E_{r}\left ( r=R_{i} \right )=E_{i}\). Si\(I\) fluye una corriente, ¿cuáles son las distribuciones de carga espacial y campo eléctrico en estado estacionario?
(b) ¿Cuál es la corriente continua\(I\) en términos del voltaje bajo condiciones limitadas de carga espacial\(\left ( E_{i}=0 \right )\)? Pista:
\(\int \frac{\left [ r^{2}-R_{i}^{2} \right ]^{1/2}}{\textrm{r}}d\textrm{r}=\left [ r^{2}-R_{i}^{2} \right ]^{1/2}-R_{i}\cos ^{-1}\left ( \frac{R_{i}}{\textrm{r}} \right ) \)
(c) ¿Para qué valor\(E_{i}\) es constante el campo eléctrico entre electrodos? ¿Cuál es la corriente resultante?
(d) Repetir (a) - (b) para electrodos esféricos concéntricos.
Sección 3.8
(a) ¿Cuánto trabajo se necesita para llevar un dipolo puntual del infinito a una posición donde está el campo eléctrico\(\textbf{E}\)?
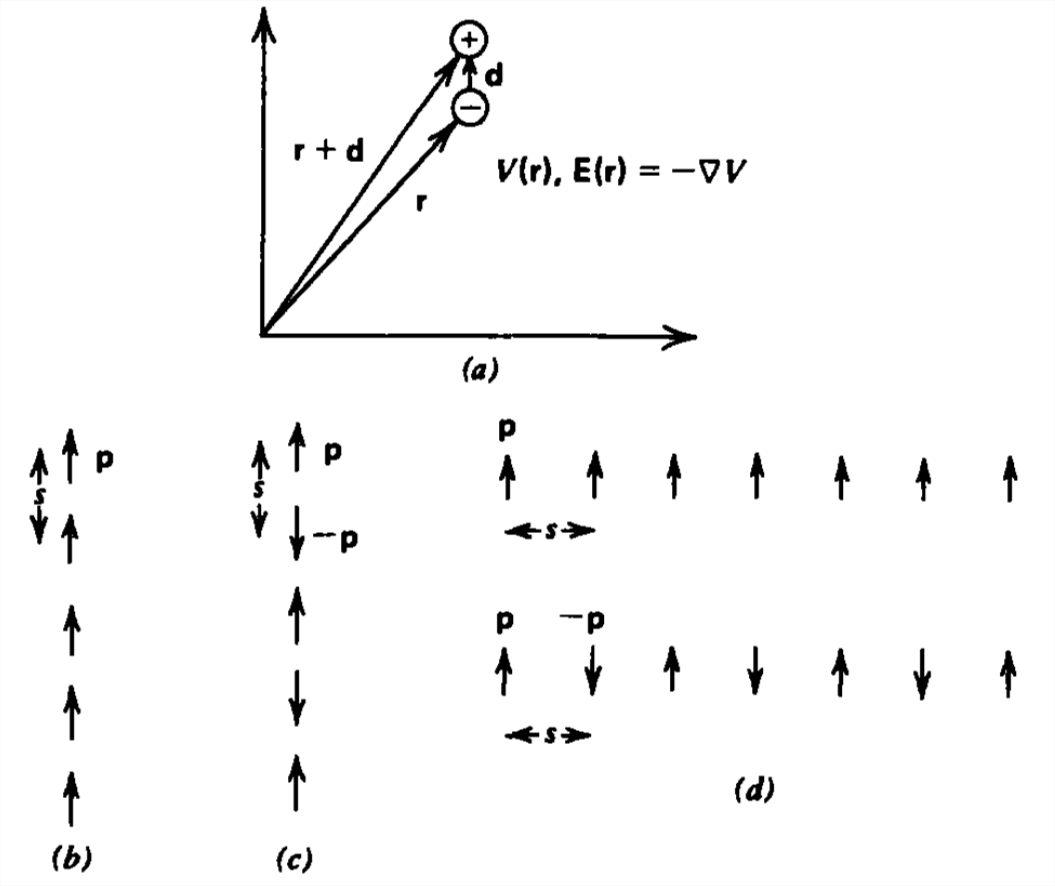
(b) Un cristal consiste en una cadena infinitamente larga de dipolos a una distancia constante s. ¿Cuál es la energía de unión del cristal? (Pista:\(\sum_{n=1}^{\infty }1/n^{3}\approx 1.2\).)
(c) Repita (b) si los momentos dipolares se alternan en señal. (Pista:\(\sum_{n=1}^{\infty }\left (-1 \right )^{n}/n^{3}\approx -0.90\).)
(d) Repetir (b) y (c) si los momentos dipolares son perpendiculares a la línea de dipolos para dipolos de polaridad idéntica o alterna.
¿Cuál es la energía almacenada en el campo de un dipolo puntual con momento\(\textbf{p}\) fuera de una esfera concéntrica circundante con radio molecular\(R\)? Pista:
\ (\ int\ cos ^ {2}\ theta\ sin\ theta d\ theta =-\ frac {\ cos ^ {3}\ theta} {3}\
\ int\ sin ^ {3}\ theta d\ theta =-\ frac {1} {3}\ cos\ theta\ izquierda (\ sin ^ {2}\ theta\ +2 derecha)\)
Una gotita esférica de radio\(R\) que lleva una carga total\(\mathcal{Q}\) en su superficie se divide en gotitas\(N\) idénticas más pequeñas.
a) ¿Cuál es el radio de cada gotita y cuánta carga lleva?
b) Suponiendo que las gotitas están muy separadas y no interactúan, ¿cuánta energía electrostática se almacena?
(c) Debido a su tensión superficial, las gotitas también tienen una energía superficial constante por unidad de área\(w_s\). ¿Cuál es la energía total (electrostática más superficie) en el sistema?
d) Cuánto trabajo se requirió para formar las gotitas y separarlas a espacios infinitos.
e) ¿Qué valor de\(N\) minimiza este trabajo? Evaluar para una gotita de agua con radio original de\(1\) mm y carga de\(10^{-6}\,\textrm{coul}\). (Para el agua\(w_{s}\approx 0.072\,\textrm{joule/m}^{2} \).)
Dos cilindros coaxiales de radios\(a\) y\(b\) transportan carga uniformemente distribuida ya sea en sus superficies o en todo el volumen. Encuentre la energía almacenada por unidad de longitud en la\(z\) dirección para cada una de las siguientes distribuciones de carga que tengan una carga total de cero:
(a) Carga superficial en cada cilindro con\(\sigma _{a}2\pi a=-\sigma _{b}2\pi b\).
(b) Cilindro interno con carga volumétrica\(\rho_{a}\) y cilindro exterior con carga superficial\(\sigma _{b}\) donde\(\sigma _{a}2\pi b=-\rho_{b}2\pi a^{2}\).
(c) Cilindro interno con carga volumétrica\(\rho_{a}\) con la región entre cilindros que tienen carga volumétrica\(\rho_{b}\) donde\(\rho _{a}\pi a^{2}=-\rho_{b}\pi \left (b^{2}-a^{2} \right )\).
Encuentra la energía de unión en los siguientes modelos atómicos:
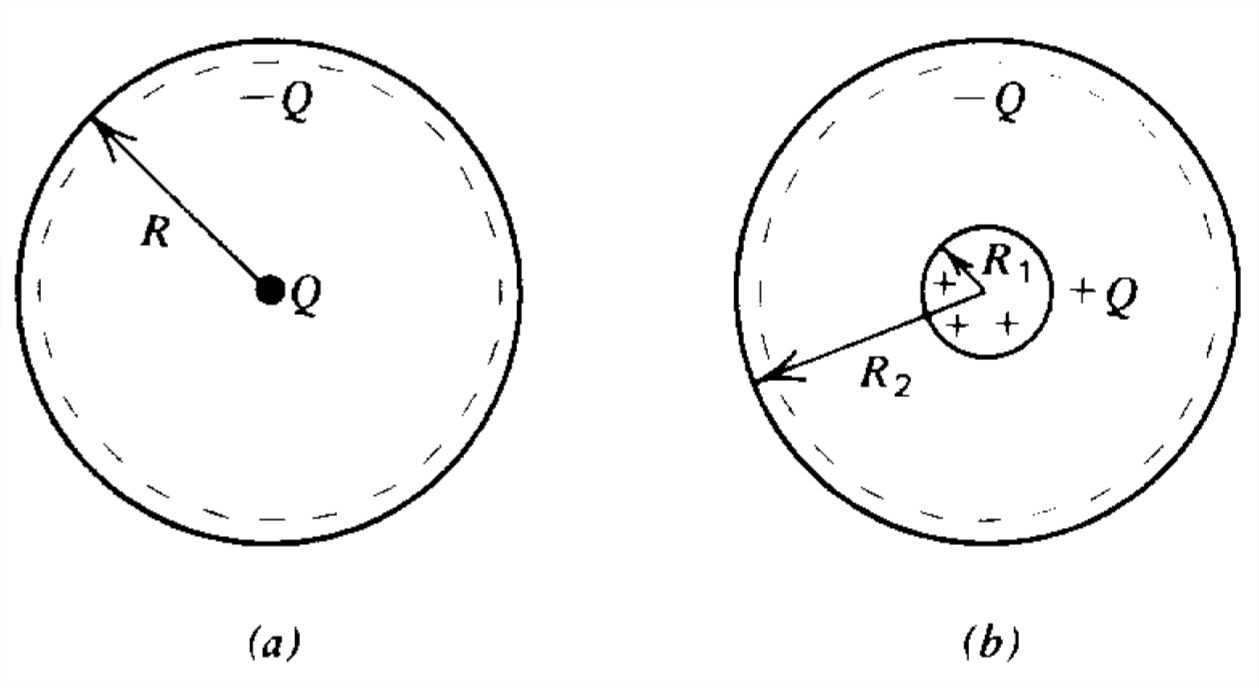
a) Una carga puntual\(\mathcal{Q}\) rodeada por una carga superficial uniformemente distributada\(-\mathcal{Q}\) de radio\(R\).
b) Una carga volumétrica uniformemente distribuida\(\mathcal{Q}\) dentro de una esfera de radio\(R_1\) rodeada en el exterior por una carga superficial uniformemente distribuida\(-\mathcal{Q}\) en el radio\(R_2\).
Un condensador\(C\) se carga a una tensión\(V_0\). En\(t = 0\) otro condensador inicialmente sin carga de igual capacitancia\(C\) se conecta a través del condensador cargado a través de algunos cables con pérdida que tienen una conductividad óhmica\(\sigma \), área de sección transversal\(A\), y. longitud total\(l\).
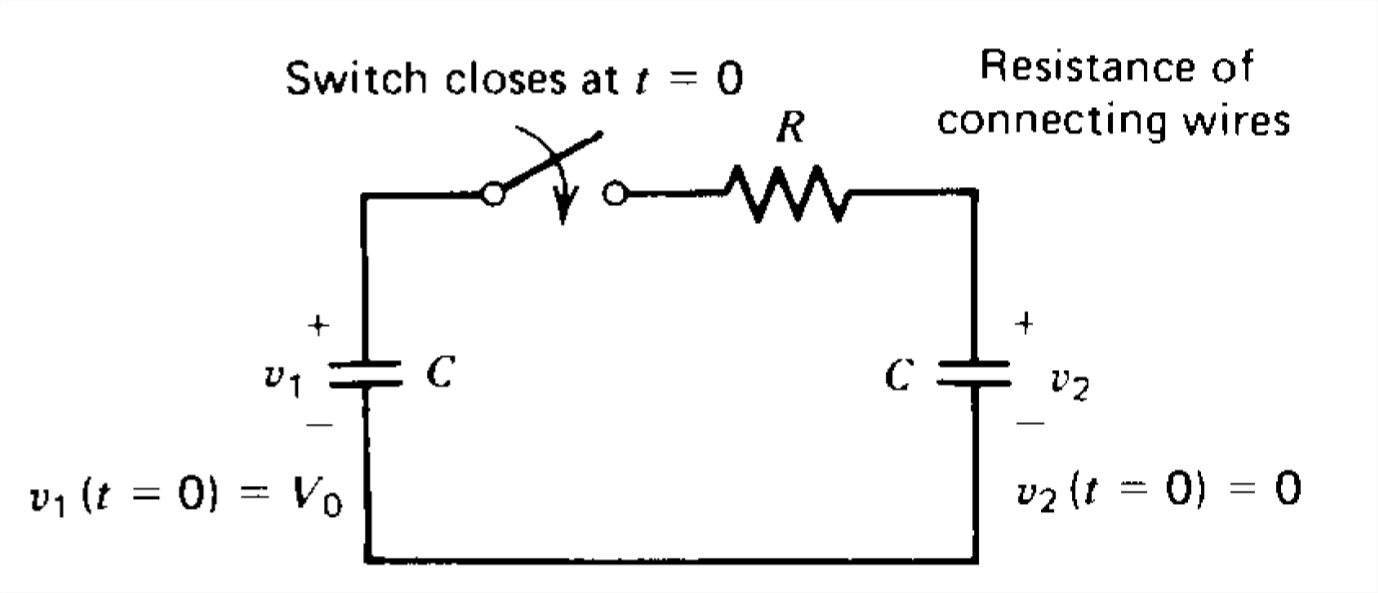
a) ¿Cuál es la energía inicial almacenada en el sistema?
(b) ¿Cuál es la corriente\(i\) y los voltajes del circuito\(v_1\) y\(v_2\) a través de cada condensador en función del tiempo?
(c) ¿Cuál es la energía total almacenada en el sistema en el estado estacionario de CC y cómo se compara con (a)?
d) ¿Cuánta energía se ha disipado en la resistencia del cable y cómo se compara con (a)?
e) ¿Cómo cambian las respuestas de (b) - (d) si el sistema no tiene pérdidas de modo que eso\(\sigma = \infty \)? ¿Cómo se disipa el poder?
(f) Si los cables son superconductores La Sección 3-2-5d mostró que la densidad de corriente está relacionada con el campo eléctrico como
\(\frac{\partial J}{\partial t}=\omega _{p}^{2}\varepsilon E\)
donde la frecuencia plasmática\(\omega _{p}\) es una constante. ¿Cuál es el circuito equivalente del sistema?
g) ¿Cuál es la dependencia temporal de la corriente ahora?
h) ¿Cuánta energía se almacena en cada elemento en función del tiempo?
(i) En cualquier momento\(t\) ¿cuál es la energía total del circuito y cómo se compara con (a)?
Sección 3.9
Un dipolo polarizado permanentemente con momento\(\textbf{p}\) está en ángulo\(\theta \) con un campo eléctrico uniforme\(\textbf{E}\).
(a) ¿Cuál es el par\(T\) en el dipolo?
b) ¿Cuánto trabajo incremental\(dW\) es necesario para girar el dipolo en un ángulo pequeño\(d\theta \)? ¿Cuál es el trabajo total requerido para mover el dipolo de\(\theta =0\) a cualquier valor de\(\theta \)? (Pista:\(dW=Td\theta \).)
(c) En general, la agitación térmica provoca que los dipolos se distribuyan en todos los ángulos de\(\theta \). Las estadísticas de Boltzmann nos dicen que la densidad numérica de los dipolos que tienen energía\(W\) son
\(n=n_{0}e^{-W/kT}\)
donde\(n_{0}\) es una constante. Si el número total de dipolos dentro de una esfera de radio\(R\) es\(N\), ¿qué es no? (Pista: Vamos\(u=\left ( pE/kT \right )\cos \theta \).)
d) Considerar una concha de dipolos dentro del rango de\(\theta \) a\(\theta +d\theta \). ¿Cuál es la magnitud y dirección de la polarización neta debido a este caparazón?
e) ¿En qué consiste la polarización total integrada\(\theta \)? Esto se conoce como la ecuación de Langevin. (Pista:\(\int ue^{u}du=\left ( u-1 \right )e^{u}\).)
(f) Incluso con un campo grande de\(E\approx 10^{6}\,\textrm{v/m}\) con un dipolo compuesto por un protón y un electrón a una distancia de\(10\,\AA \left ( 10^{-9} \,\textrm{m}\right )\) separación, mostrar que a temperatura ambiente la cantidad\(\left ( pE/kT \right )\) es mucho menor que la unidad y ampliar los resultados de (e). (Pista: Será necesario ampliar (e) hasta tercer orden en\(\left ( pE/kT \right )\).
g) En este límite ¿cuál es la polarizabilidad orientacional?
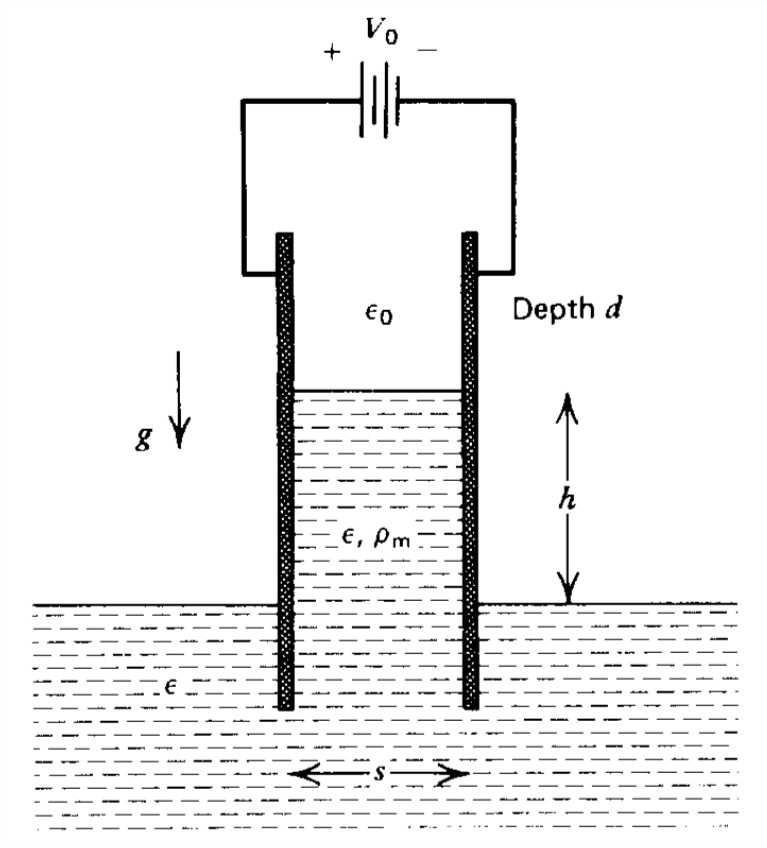
Un par de electrodos de placa paralelos\(s\) separados a una distancia a una diferencia de voltaje\(V_0\) se sumerge en un fluido dieléctrico de permitividad\(\varepsilon \). El fluido tiene una densidad de masa\(\rho _{m}\) y la gravedad actúa hacia abajo. ¿Qué tan alto sube el líquido entre las placas?
Los electrodos de placa paralela a diferencia de voltaje\(V_0\) encierran un dieléctrico elástico con permitividad\(\varepsilon \). La fuerza eléctrica de atracción entre los electrodos se equilibra con la fuerza elástica del dieléctrico.
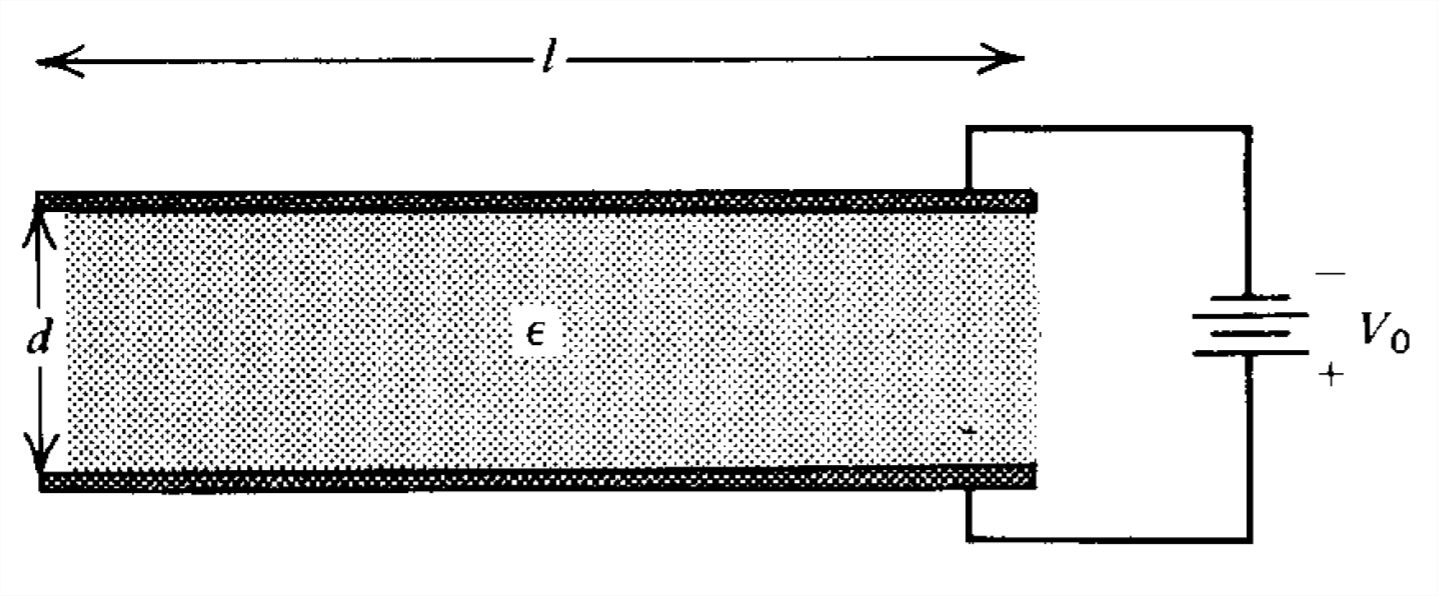
(a) Cuando el espaciado entre electrodos es\(d\) ¿cuál es la densidad de carga superficial libre en el electrodo superior?
b) ¿Cuál es la fuerza eléctrica por unidad de área que ejerce el electrodo sobre la interfaz dieléctrica?
c) La fuerza elástica restauradora por unidad de superficie viene dada por la relación
\(F_{A}=Y\ln \frac{d}{d_{0}}\)
donde\(Y\) es el módulo de elasticidad y\(d_{0}\) es el\(\left ( V_{0}=0 \right )\) espesor no estresado del dieléctrico. Escribir una expresión trascendental para el espesor de equilibrio del dieléctrico.
d) ¿Cuál es el espesor dieléctrico de equilibrio mínimo y a qué voltaje se produce? Si se aplica un voltaje mayor no hay equilibrio y el dieléctrico se fractura ya que la tensión eléctrica supera la fuerza elástica restauradora. A esto se le llama la teoría de la ruptura electromecánica. [Ver K. H. Stark y C. G. Garton, Fuerza Eléctrica del Politeno Irradiado, Nature 176 (1955) 1225-26.]
Un electreto con polarización permanente\(P_{0}\textbf{i}_{y}\) y espesor llena\(d\) parcialmente un condensador de espacio libre. No hay carga superficial en la interfaz de espacio libre electret.
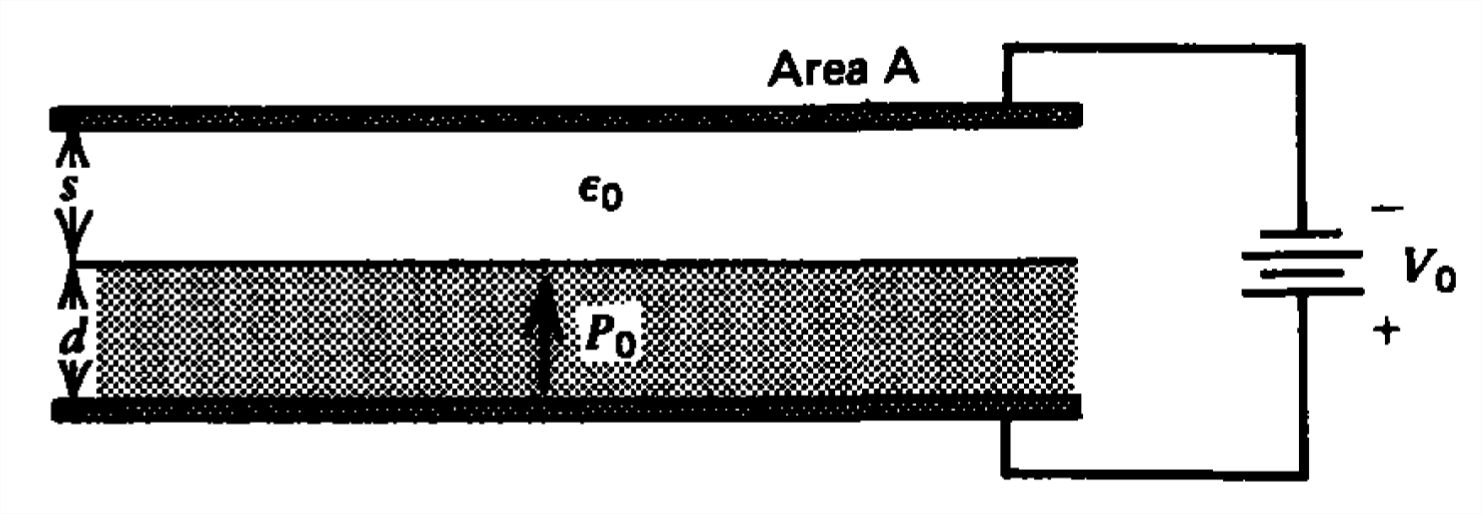
a) ¿Cuáles son los campos eléctricos en cada región?
b) ¿Cuál es la fuerza sobre el electrodo superior?
Una distribución uniforme de carga libre con densidad\(\rho _{0}\) es entre electrodos de placa paralelos a diferencia de potencial\(V_0\).
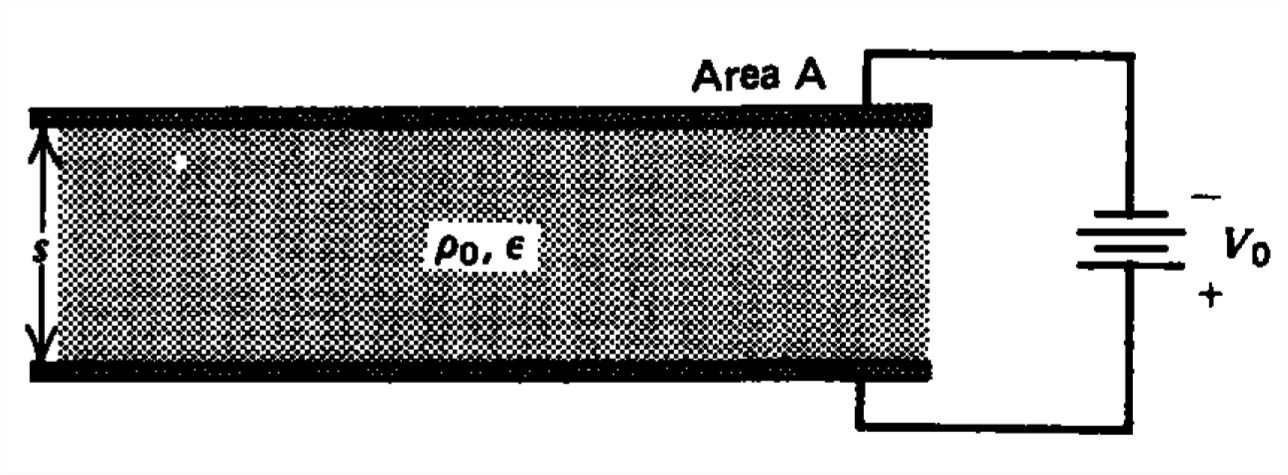
a) ¿Cuál es la energía almacenada en el sistema?
(b) Comparar la capacitancia con aquella cuando\(\rho _{0}=0\).
c) ¿Cuál es la fuerza total en cada electrodo y en la distribución de carga volumétrica?
d) ¿Cuál es la fuerza total sobre el sistema?
Los electrodos cilíndricos coaxiales a diferencia de voltaje\(V_0\) se llenan parcialmente con un material polarizado. Encuentra la fuerza sobre este material si es
a) permanentemente polarizadas como\(P_{0}\textbf{i}_{r}\);
b) polarizadas linealmente con permitividad\(\varepsilon \).
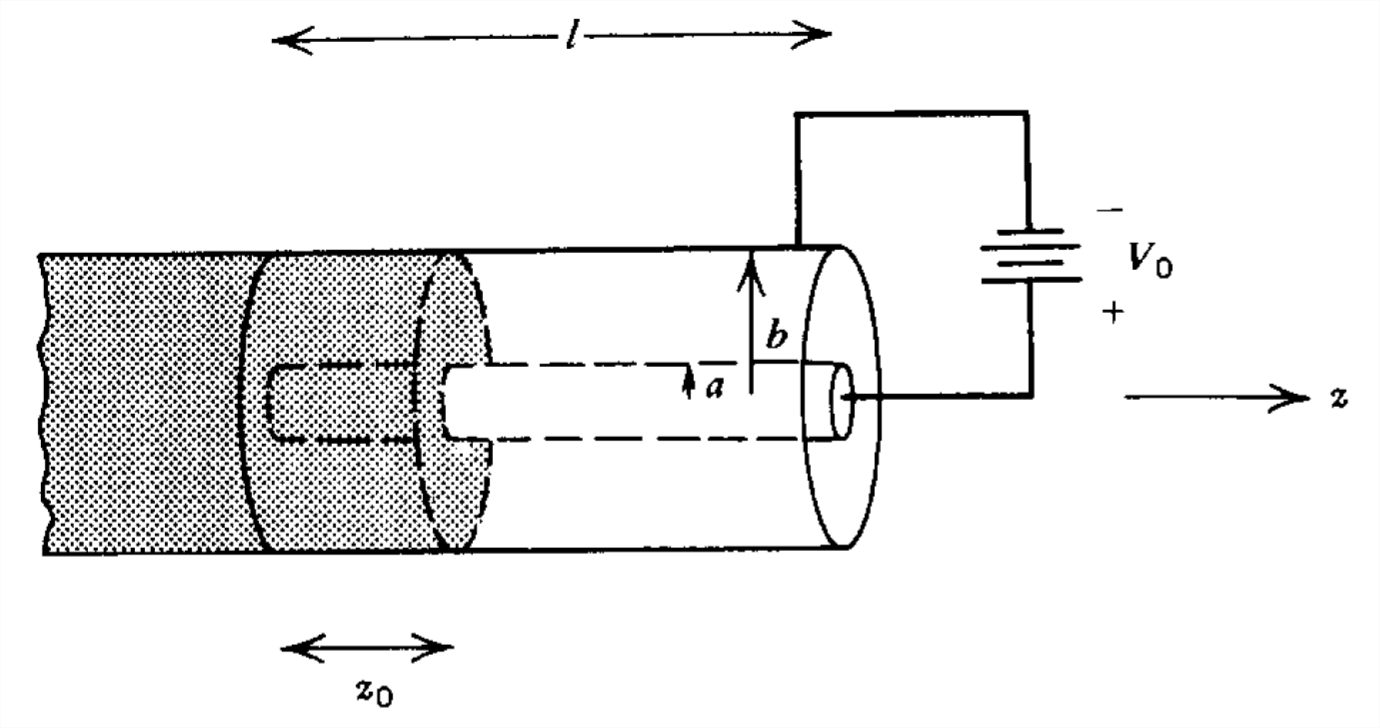
El electrodo superior de un par a diferencia de potencial constante\(V_0\) es libre de deslizarse en la\(x\) dirección. ¿Cuál es el\(x\) componente de la fuerza en el electrodo superior?
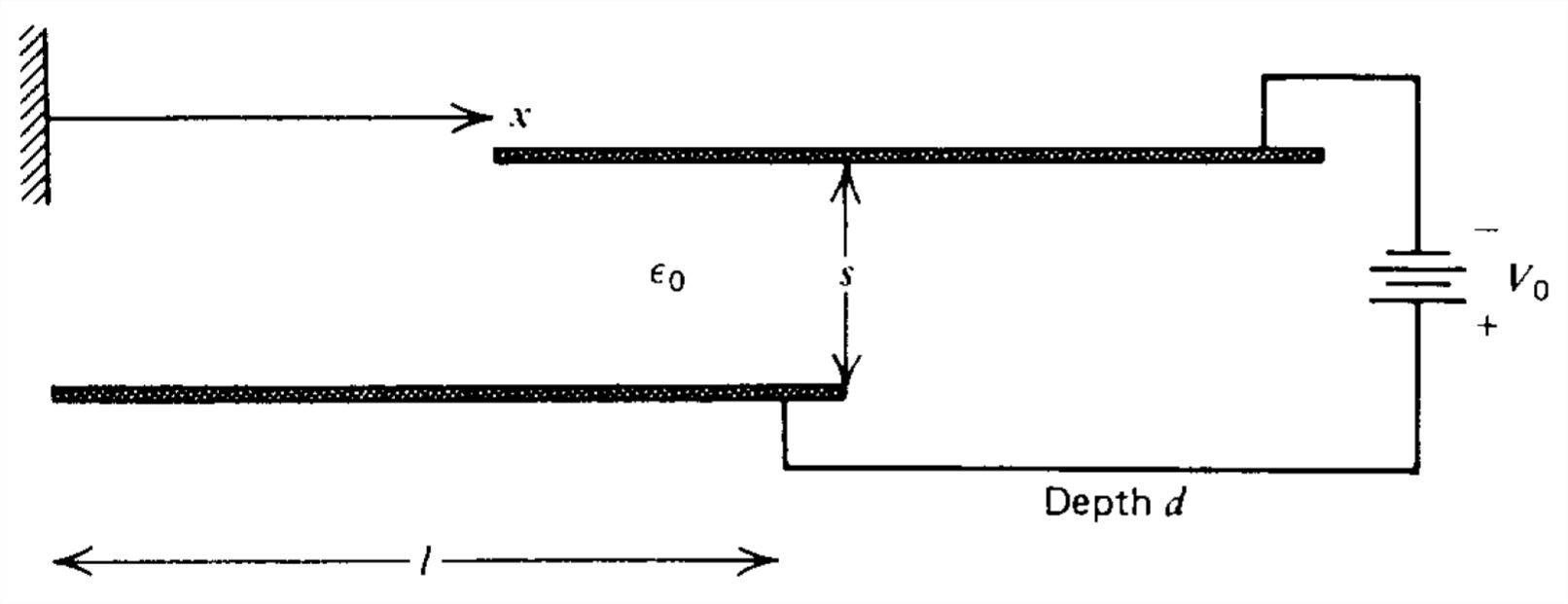
Un condensador tiene una parte móvil que puede girar a través del ángulo\(\theta \) para que la capacitancia\(C\left ( \theta \right )\) dependa de\(\theta\).
(a) ¿Cuál es el par de torsión en la parte móvil?
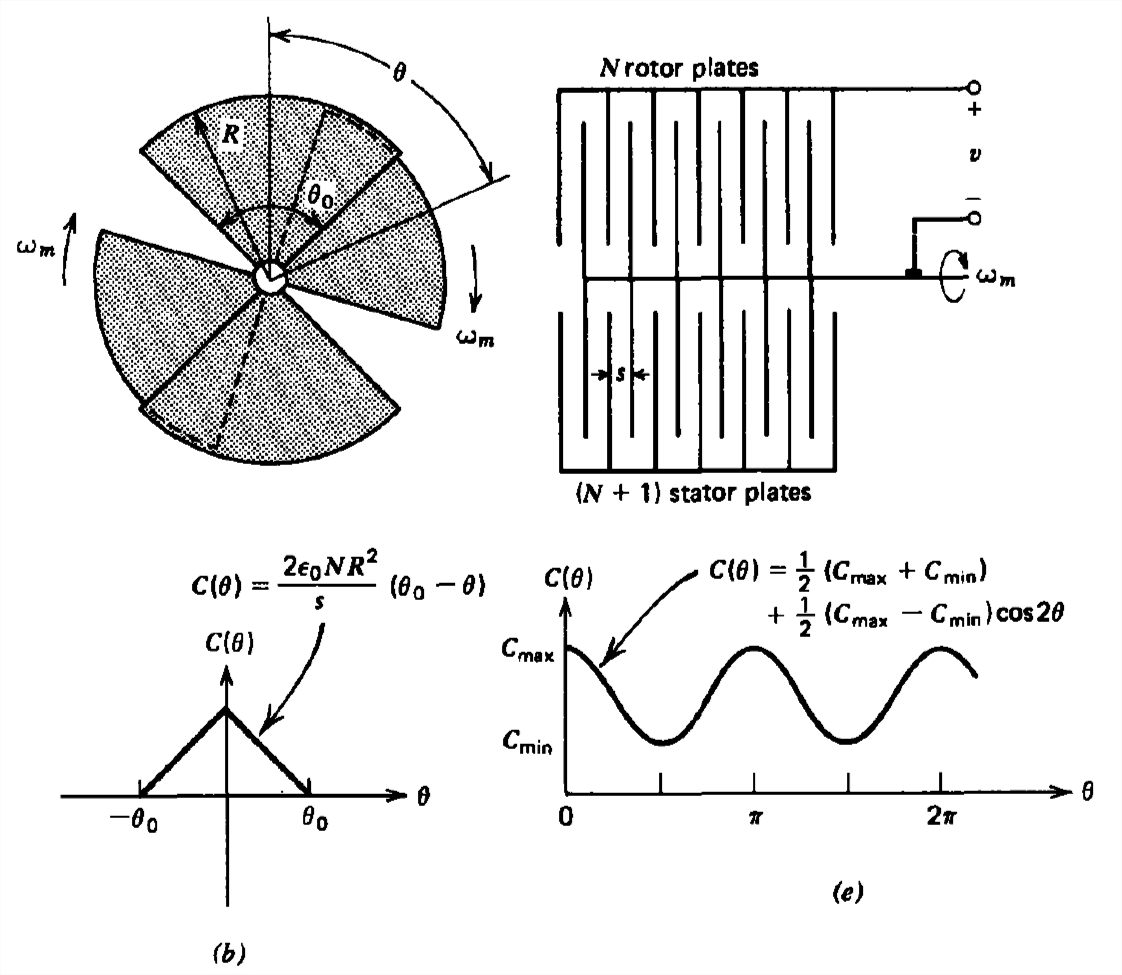
(b) Un voltímetro electrostático consiste en electrodos\(N+1\) fijos en forma de pastel al mismo potencial intercalados con\(N\) placas montadas en un eje que es libre de girar para\(-\theta _{0}< \theta < \theta _{0}\). ¿Cuál es la capacitancia en función de\(\theta\)?
(c) Se\(v\) aplica un voltaje. ¿Cuál es el par eléctrico en el eje?
(d) Un resorte torsional ejerce un par restaurador sobre el eje
\(T_{s}=-K\left ( \theta -\theta _{s} \right )\)
donde\(K\) es la constante de resorte y\(\theta _{s}\) es la posición de equilibrio del eje a cero voltaje. ¿Cuál es la posición de equilibrio del eje cuando\(v\) se aplica el voltaje? Si se aplica una tensión sinusoidal, ¿cuál es la desviación angular promedio en el tiempo\(<\theta>\)?
(e) Se retira el resorte torsional para que el eje pueda girar libremente. Los efectos de campo de franja hacen que la capacitancia varíe suavemente entre los valores mínimo y máximo de un valor de CC más un solo término espacial sinusoidal
\(C\left ( \theta \right )=\frac{1}{2}\left [ C_{\textrm{max}}+C_{\textrm{min}} \right ]+\frac{1}{2}\left [ C_{\textrm{max}}-C_{\textrm{min}} \right ]\cos 2\theta \)
Se aplica un voltaje\(V_{0}\cos \omega t\) sinusoidal. ¿Cuál es el par instantáneo en el eje?
(f) Si el eje gira a velocidad angular constante de\(\omega _{m}\) manera que
\(\theta =\omega _{m}t+\delta \)
¿dónde\(\delta \) está el ángulo del eje\(t =0\), bajo qué condiciones es el par en (e) una constante? Pista:
\(\begin{align}\sin 2\theta \cos ^{2}\omega t&=\frac{1}{2}\sin 2\theta \left ( 1+\cos 2\omega t \right )\notag \\ &=\frac{1}{2}\sin 2\theta +\frac{1}{4}\left [ \sin \left (2\left ( \omega t+\theta \right ) \right )-\sin \left (2\left ( \omega t-\theta \right ) \right ) \right ] \end{align}\)
(g)\(T_{0}\) Se requiere un par promedio de tiempo del eje. ¿Cuál es el ángulo de torsión\(\delta \)?
(h) ¿Cuál es el par máximo que se puede entregar? Esto se llama el torque de extracción. ¿En qué ángulo\(\delta \) ocurre esto?
Sección 3-10
El cinturón de un generador Van de Graaff tiene ancho\(w\) y se mueve con velocidad\(U\) llevando una carga superficial\(\sigma _{f}\) hasta la cúpula esférica de radio\(R\).
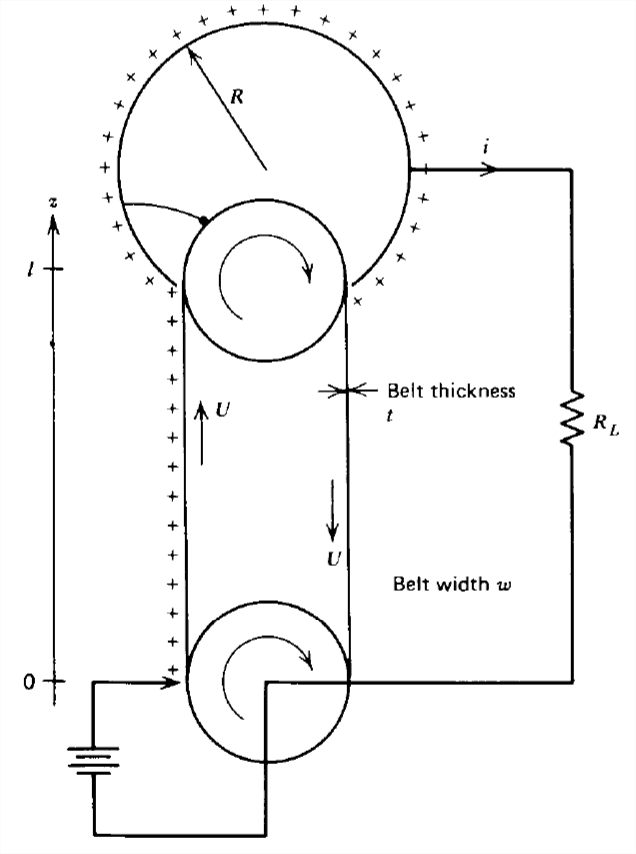
a) ¿Cuál es la dependencia temporal del voltaje del domo?
b) Suponiendo que el potencial eléctrico varía linealmente entre el punto de carga y el domo, ¿cuánta energía en función del tiempo se requiere para que el motor gire la correa?
Un generador Van de Graaff tiene una correa con pérdida con conductividad óhmica\(\sigma\) que viaja a velocidad constante\(U\). El punto de carga en\(z = 0\) mantiene una densidad de carga de volumen constante\(\rho _{0}\) en la cinta en\(z =0\). El domo es cargado por una resistencia\(R_L\) a tierra.
(a) Asumiendo solo variaciones unidimensionales con\(z\), ¿cuáles son las distribuciones de carga volumétrica en estado estacionario, campo eléctrico y densidad de corriente en la banda?
b) ¿Cuál es el voltaje del domo en estado estacionario?
Un par de máquinas de inducción electrostática acopladas tienen sus electrodos inductores conectados a través de una resistencia de carga\(R_L\). Además, cada electrodo tiene una resistencia\(R\) a las fugas a tierra.
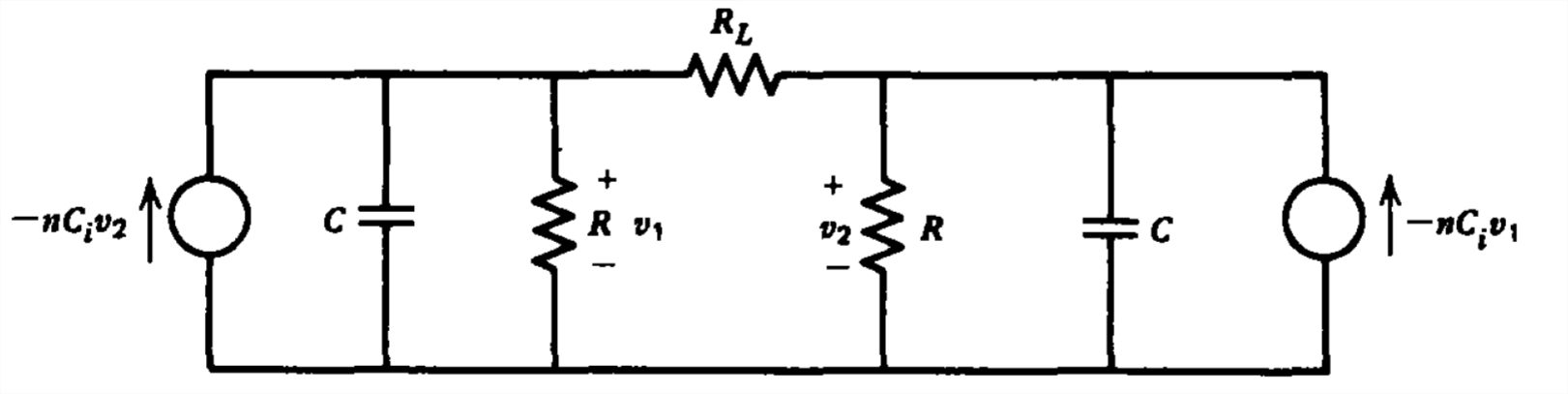
(a) ¿Para qué valores de\(n\), el número de conductores por segundo que pasan por el colector, la máquina se autoexcitará?
b) Si\(n=10\), y\(C=10\,\textrm{pf}\) con\(C_i=2\,\textrm{pf}\)\(R_L=R\), ¿cuál es el valor mínimo de\(R\) para la autoexcitación?
(c) Si tenemos tres máquinas acopladas de este tipo, ¿cuál es la condición para la autoexcitación y cuáles son las frecuencias de oscilación si\(R_{L}= \infty \)?
(d) Repetir (c) para\(N\) tales máquinas acopladas con\(R_{L}= \infty \). La última máquina está conectada a la primera.


