4.2: Problemas de valor límite en geometrías cartesianas

Para la mayoría de los problemas tratados en los Capítulos 2 y 3 nos limitamos a problemas unidimensionales donde el campo eléctrico apunta en una sola dirección y solo depende de esa coordenada. Para muchos casos, el volumen es gratuito por lo que el sistema es descrito por la ecuación de Laplace. La carga superficial está presente solo en los límites interfaciales que separan materiales conductores diferentes. Ahora consideramos tales problemas de volumen sin carga con variaciones bidimensionales y tridimensionales.

4-2-1 Separación de Variables

Supongamos que dentro de una región de espacio de permitividad constante sin carga de volumen, esas soluciones no dependen de la coordenada z. Entonces la ecuación de Laplace se reduce a

\[\frac{\partial^{2}V}{\partial x^{2}} + \frac{\partial^{2}V}{\partial y^{2}} = 0 \nonumber \]

Intentamos una solución que es producto de una función solo de la coordenada x y una función solo de y:

\[V(x,y) = X (x) Y(y) \nonumber \]

Esta supuesta solución suele ser conveniente de usar si los límites del sistema se encuentran en planos x o y constantes. Entonces a lo largo de un límite, una de las funciones en (2) es constante. Cuando (2) se sustituye en (1) tenemos

\[Y \frac{d^{2}X}{dx^{2}} + X \frac{d^{2}Y}{dy^{2}} = 0 \Rightarrow \frac{1}{X} \frac{d^{2}X}{dx^{2}} + \frac{1}{Y} \frac{d^{2}Y}{dy^{2}} = 0 \nonumber \]

donde las derivadas parciales se convierten en derivadas totales porque cada función sólo depende de una sola coordenada. La segunda relación se obtiene dividiendo por XY de manera que el primer término es sólo una función de x mientras que el segundo es sólo una función de y.

La única forma en que la suma de estos dos términos puede ser cero para todos los valores de x e y es si cada término es por separado igual a una constante de manera que (3) se separe en dos ecuaciones,

\[\frac{1}{X} \frac{d^{2}X}{dx^{2}} = k^{2}, \: \: \: \frac{1}{Y} \frac{d^{2}Y}{dy^{2}} = -k^{2} \nonumber \]

donde k ² se llama la constante de separación y en general puede ser un número complejo. Estas ecuaciones pueden entonces ser reescritas como las ecuaciones diferenciales ordinarias:

\[\frac{d^{2}X}{dx^{2}} - k^{2}X = 0, \: \: \: \: \frac{d^{2} Y}{dy^{2}} + k^{2} Y =0 \nonumber \]

4-2-2 Soluciones Constantes de Separación Cero

Cuando la constante de separación es cero (k ² =0) las soluciones a (5) son

\[X = a_{1}x + b_{1}, \: \: \: \: Y = c_{1}y + d_{1} \nonumber \]

donde a ₁, b ₁, c ₁ y d ₁ son constantes. El potencial viene dado por el producto de estos términos que es de la forma

\[V = a_{2} + b_{2}x + c_{2}y + d_{2}xy \nonumber \]

Los términos lineales y constantes que hemos visto antes, como la distribución de potencial dentro de un condensador de placa paralela sin franja, de manera que el campo eléctrico es uniforme. El último término no hemos visto previamente.

(a) Electrodos hiperbólicos

Un electrodo de forma hiperbólica cuya forma superficial obedece a la ecuación xy = ab está en el potencial V _o y se coloca sobre una esquina de ángulo recto conectado a tierra como en la Figura 4-1. El

Figura 4-1 Las líneas equipotenciales y de campo para un electrodo de forma hiperbólica a un potencial V _o por encima de una esquina conductora de ángulo recto son hipérbolas ortogonales.

las condiciones de contorno son

\[V(x=0) = 0, \: \: \: \: V(y=0) = 0, \: \: \: V(y=0) = 0, \: \: \: \: V(xy=ab) = V_{0} \nonumber \]

para que la solución se pueda obtener de (7) como

\[V (x,y) = V_{0} xy/(ab) \nonumber \]

El campo eléctrico es entonces

\[\textbf{E} = - \nabla V = - \frac{V_{0}}{ab}[y \textbf{i}_{x} + x \textbf{i}_{y}] \nonumber \]

Las líneas de campo dibujadas en la Figura 4-1 son la familia perpendicular de hipérbolas a las hipérbolas equipotenciales en (9):

\[\frac{dy}{dx} = \frac{E_{y}}{E_{x}} = \frac{x}{y} \Rightarrow y^{2} - x^{2} = \textrm{const} \nonumber \]

(b) Resistencia en una Caja Abierta

Un medio resistivo está contenido entre dos electrodos, uno de los cuales se extiende por encima y se dobla a través de una esquina en ángulo recto como en la Figura 4-2. Intentamos constante de separación cero

Figura 4-2: Un medio resistivo llena parcialmente una caja conductora abierta

soluciones dadas por (7) en cada región encerrada por los electrodos:

\[V = \left \{ \begin{matrix} a_{1} + b_{1} x + c_{1} y + d_{1}xy, & 0 \leq y \leq d \\ a_{2} + b_{2}x + c_{2}y + d_{2}xy, & d \leq y \leq s \end{matrix} \right. \nonumber \]

Con el potencial limitado en los electrodos y siendo continuo a través de la interfaz, las condiciones límite son

\[V (x=0) = V_{0} = a_{1} + C_{1}y \Rightarrow a_{1} = V_{0}, \: \: \: c_{1} = 0 \: \: \: \: \: \: (0 \leq y \leq d) \\ V(x=l) = 0 = \left \{ \begin{matrix} \underbrace{a_{1}}_{V_{0}} + b_{1} l + c_{1} \nearrow^{0} y + d_{1} ly \Rightarrow b_{1} = - V_{0}/l, & d_{1}=0 & (0 \leq y \leq d) \\ a_{2} +b_{2}l + c_{2}y + d_{2} ly \Rightarrow a_{2} + b_{2}l = 0, & c_{2} + d_{2}l = 0 & (d \leq y \leq s) \end{matrix} \right. \\ V(y=s) = 0 = a_{2} + b_{2}x + c_{2}s + d_{2} xs \Rightarrow a_{2} + c_{2}s = 0, \: \: \: b_{2} + d_{2}s = 0 \\ V(y = d_{+}) = V (y = d_{-}) = a_{1} + b_{1}x + c \nearrow^{0} d + d \nearrow^{0}_{1} xd \\ = a_{2} + b_{2}x + c_{2}d + d_{2} xd \\ \Rightarrow a_{1} = V_{0} = a_{2} + c_{2}d, \: \: \: b_{1} = -V_{0}/l = b_{2} + d_{2}d \nonumber \]

de manera que las constantes en (12) son

\[a_{1}=V_{0}, \: \: \: \: b_{1} = -V_{0}/l, \: \: \: \: c_{1} = 0, \: \: \: \: d_{1} = 0 \\ a_{2} = \frac{V_{0}}{(1-d/s)}, \: \: \: \: b_{2} = - \frac{V_{0}}{l(1-d/s)}, \\ c_{2} = - \frac{V_{0}}{s(1-d/s)}, \: \: \: \: d_{2} = \frac{V_{0}}{ls(1-d/s)} \nonumber \]

El potencial de (12) es entonces

\[V = \left \{ \begin{matrix} V_{0} (1-x/l), & 0 \leq y \leq d \\ \frac{V_{0}s}{s-d} \bigg(1 - \frac{x}{l} - \frac{y}{s} + \frac{xy}{ls} \bigg), & d \leq y \leq s \end{matrix} \right. \nonumber \]

con campo eléctrico asociado

\[\textbf{E} = - \nabla V = \left \{ \begin{matrix} \frac{V_{0}}{l} \textbf{i}_{x}, & 0 \leq y \leq d \\ \frac{V_{0}s}{s-d} \bigg[ \frac{\textbf{i}_{x}}{l} \bigg( 1 - \frac{y}{s} \bigg) + \frac{\textbf{i}_{y}}{s} \bigg(1 - \frac{x}{l} \bigg) \bigg], & d<y<s \end{matrix} \right. \nonumber \]

Tenga en cuenta que en el estado estacionario de CC, la conservación de la condición de límite de carga de la Sección 3-3-5 requiere que ninguna corriente cruce las interfaces en y = 0 e y = d debido a las regiones circundantes de conductividad cero. La corriente y, por lo tanto, el campo eléctrico dentro del medio resistivo debe ser puramente tangencial a las interfaces, E, (y=d..) =E, (y=0+) =0. La densidad de carga superficial en la interfaz en y = d se debe entonces solo al campo eléctrico normal arriba, como abajo, el campo es puramente tangencial:

\[\sigma_{f}(y=d) = \varepsilon_{0}E_{y}(y = d_{+}) - \varepsilon E_{y} \nearrow^{0} (y = d_{-}) = \frac{\varepsilon_{0}V_{0}}{s-d} \bigg(1-\frac{x}{l} \bigg) \nonumber \]

La fuerza cortante interfacial es entonces

\[F_{x} = \int_{0}^{l} \sigma_{f}E_{x}(y=d)w \: dx = \frac{\varepsilon_{0} V_{0}^{2}}{2(s-d)} w \nonumber \]

Si el material resistivo es líquido, esta fuerza de cizallamiento se puede utilizar para bombear el fluido. *

4-2-3 Soluciones Constantes de Separación Noncero

Otras soluciones a (5) con constante de separación distinta de cero (\(k^{2} \neq 0\)) son

\[X = A_{1} \sinh kx + A_{2} \cosh kx = B_{1} e^{kx} + B_{2} e^{-kx} \\ Y = C_{1} \sin ky + C_{2} \cos ky = D_{1} e^{jky} + D_{2} e^{-jky} \nonumber \]

Cuando k es real, las soluciones de X son hiperbólicas o equivalentemente exponenciales, como se dibuja en la Figura 4-3, mientras que las de Y son trigonométricas. Si k es puro imaginario, entonces X se vuelve trigonométrico e Y es hiperbólico (o exponencial).

La solución al potencial viene dada entonces por el producto de X e Y:

\[V = E_{1} \sin ky \sinh kx + E_{2} \sin ky \cosh kx + E_{3} \cos ky \sinh kx + E_{4} \cos ky \cosh kx \nonumber \]

o equivalentemente

\[\textrm{V} = F_{1} \sin ky e^{kx} + F_{2} \sin ky e^{-kx} + F_{3} \cos ky e^{kx} + F_{4} \cos kye^{-kx} \nonumber \]

Siempre podemos agregar las soluciones de (7) o cualquier otra solución laplaciana a (20) y (21) para obtener una solución más general

Figura 4-3 Las funciones exponenciales e hiperbólicas para argumentos positivos y negativos.

porque la ecuación de Laplace es lineal. Los valores de los coeficientes y de k están determinados por condiciones de contorno.

Cuando las regiones del espacio son de extensión infinita en la dirección x, a menudo es conveniente usar las soluciones exponenciales en (21) ya que es obvio qué soluciones decaen a medida que x se acerca\(\pm \infty\). Para regiones de extensión finita, suele ser más conveniente usar las expresiones hiperbólicas de (20). Una propiedad general de las soluciones de Laplace es que son oscilatorias en una dirección y decaen en la dirección perpendicular.

* Véase J. R. Melcher y G. I. Taylor, Electrohydrodynamics: A Review of the Role of Interfacial Shear Tenses, Annual Rev. Fluid Mech. , Vol. 1, Reseñas Anuales, Inc., Palo Alto, Calif., 1969, ed. por Sears y Van Dyke, pp. 111-146. Véase también J. R. Melcher, “Campos eléctricos y medios móviles”, película producida para el Comité Nacional de Películas de Ingeniería Eléctrica por el Centro de Desarrollo Educativo, 39 Chapel St., Newton, Misa. 02160. Esta película se describe en IEEE Trans. Educación E-17, (1974) pp. 100-110.

4-2-4 Excitación espacialmente periódica

Una hoja en el plano x =0 tiene el potencial periódico impuesto,\(V = V_{0} \sin ay\) mostrado en la Figura 4-4. Para cumplir con esta condición límite utilizamos la solución de (21) con k = a. El potencial debe permanecer finito lejos de la fuente así

Figura 4-4 El potencial y el campo eléctrico decaen lejos de una hoja infinita con voltaje espacialmente periódico impuesto. Las líneas de campo emanan de la carga superficial positiva en la hoja y terminan en la carga superficial negativa.

escribimos la solución por separado para x positivo y negativo como

\[V = \left \{ \begin{matrix} V_{0} \sin ay \: e^{-ax}, & x \geq 0 \\ V_{0} \sin ay \: e^{ax}, & x \leq 0 \end{matrix} \right. \nonumber \]

donde escogimos los coeficientes de amplitud para que sean continuos y coincidan con la excitación a x = 0. El campo eléctrico es entonces

\[\textbf{E} = - \nabla V = \left \{ \begin{matrix} -V_{0}a \: e^{-ax} [ \cos \: ay \textbf{i}_{y} - \sin \: ay \textbf{i}_{x}], & x>0 \\ -V_{0}a \: e^{ax} [ \cos \: ay \textbf{i}_{y} + \sin \: ay \textbf{i}_{x}], & x<0 \end{matrix} \right. \nonumber \]

La densidad de carga superficial en la lámina viene dada por la discontinuidad en el componente normal de D a través de la lámina:

\[\sigma_{f}(x=0) = \varepsilon [ E_{x} (x = 0_{+}) - E_{x} (x = 0_{-})] \\ 2 \varepsilon V_{0} a \: \sin \: ay \nonumber \]

Las líneas de campo dibujadas en la Figura 4-4 obedecen a la ecuación

\[\frac{dy}{dx} = \frac{E_{y}}{E_{x}} = \mp \cot \: ay \Rightarrow \cos \: ay e^{mp ax} = \textrm{const} \left \{ \begin{matrix} x>0 \\ x<0 \end{matrix} \right. \nonumber \]

4-2-5 Armónicos Rectangulares

Cuando las excitaciones no son sinusoidalmente periódicas en el espacio, se pueden hacer expresándolas en términos de una serie trigonométrica de Fourier. Cualquier función periódica de y se puede expresar como una suma infinita de términos sinusoidales como

\[f(y) = \frac{1}{2} b_{0} + \sum_{n=1}^{\infty} \bigg(a_{n} \: \sin \frac{2n \pi y}{\lambda} + b_{n} \cos \frac{2n \pi y}{\lambda} \bigg) \nonumber \]

donde\(\lambda\) es el periodo fundamental de f (y).

Los coeficientes de Fourier a _n se obtienen multiplicando ambos lados de la ecuación por sin (\(2 p \pi y/\lambda\)) e integrándose a lo largo de un periodo. Dado que el parámetro p es independiente del índice n, podemos llevar el término dentro de la suma en el lado derecho. Debido a que las funciones trigonométricas son ortogonales entre sí, se integran a cero excepto cuando la función se multiplica a sí misma:

\[\int_{0}^{\lambda} \sin \frac{2 p \pi y}{\lambda} \sin \frac{2n \pi y}{\lambda} dy = \left \{ \begin{matrix} 0, & p \neq n \\ \lambda/2, & p = n \end{matrix} \right. \\ \int_{0}^{\lambda} \sin \frac{2 p \pi y}{\lambda} \cos \frac{2 n \pi y}{\lambda} dy = 0 \nonumber \]

Cada término de la serie para\(n \neq p\) se integra a cero. Solo el término para n = p es distinto de cero por lo que

\[a_{p} = \frac{2}{\lambda} \int_{0}^{\lambda} f(y) \sin \frac{2 p \pi y}{\lambda} dy \nonumber \]

Para obtener los coeficientes b _n, de manera similar multiplicamos por cos (\(2 p \pi y/\lambda\)) e integramos a lo largo de un periodo:

\[b_{p} = \frac{2}{\lambda} \int_{0}^{\lambda} f(y) \cos \frac{2 p \pi y}{\lambda} dy \nonumber \]

Considere la caja rectangular conductora de extensión infinita en las direcciones x y z y de ancho d en la dirección y que se muestra en la Figura 4-5. El potencial a lo largo del borde x = 0 es V _o mientras que todas las demás superficies están conectadas a tierra a potencial cero. Cualquier función periódica se puede utilizar para f (y) si sobre el intervalo\(0 \leq y \leq d, f(y)\) tiene las propiedades

\[f(y) = V_{0}, 0< y< d; f(y=0) = f(y=d) =0 \nonumber \]

Figura 4-5 Una caja conductora abierta de extensión infinita en las direcciones x y z y de ancho finito d en la dirección y, tiene potencial cero en todas las superficies excepto el extremo cerrado en x = 0, donde V = V ₀.

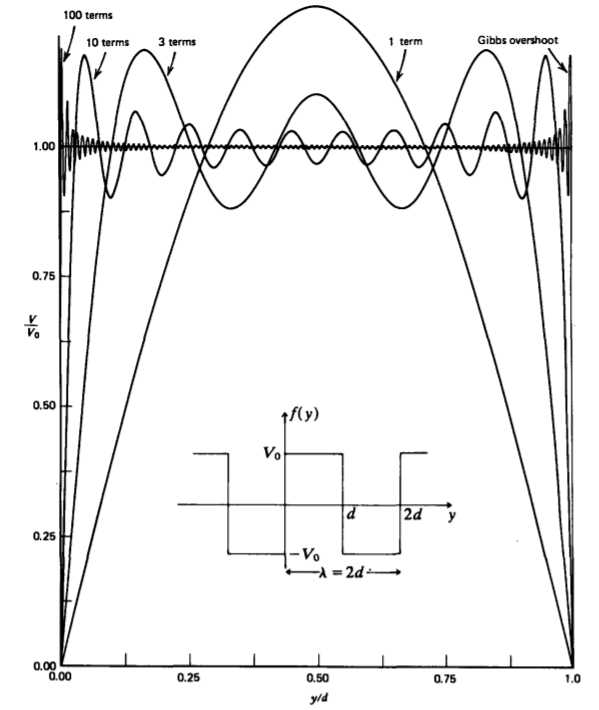
En particular, elegimos la función de onda cuadrada periódica con la que\(\lambda = 2d\) se muestra en la Figura 4-6 para que realizar las integraciones en (28) y (29) rinda

\[a_{p} = - \frac{2 V_{0}}{p \pi} (\cos p \pi - 1) \\ = \left \{ \begin{matrix} 0, & p \textrm{ even} \\ 4 V_{0}/p \pi, & p \textrm{ odd} \end{matrix} \right. \\ b_{p} = 0 \nonumber \]

Así, el potencial constante en x =0 puede escribirse como la serie sinusoidal de Fourier

\[V(x=0) = V_{0} = \frac{4 V_{0}}{\pi} \sum_{n=1 \\ n \textrm{ odd}}^{\infty} \frac{\sin (n \pi y/d)}{n} \nonumber \]

En la Figura 4-6 representamos varias sumas parciales de la serie de Fourier para mostrar que a medida que el número de términos tomados se vuelve grande, la serie se acerca al valor constante V ₀ excepto por el sobreimpulso de Gibbs de aproximadamente 18% a y = 0 e y = d donde el la función es discontinua.

La ventaja de escribir V ₀ en una serie sinusoidal de Fourier es que cada término de la serie tiene una solución similar a la encontrada en (22) donde la constante de separación para cada término es\(k_{n} =n \pi /d\) con amplitud asociada\(4 V_{0} /(n \pi)\).

La solución es solo distinta de cero para x > 0 así que inmediatamente escribimos la solución potencial total como

\[V(x,y) = \frac{4V_{0}}{\pi} \sum_{n=1 \\ n \textrm{ odd}}^{\infty} \frac{1}{n} \sin \frac{n pi y}{d} e^{-n \pi x /d} \nonumber \]

Figura 4-5 para varias sumas parciales. A medida que aumenta el número de términos, la serie se acerca a una constante excepto en los límites donde la discontinuidad en el potencial da lugar al fenómeno de Gibbs de un 18% de sobreimpulso con ancho estrecho.

El campo eléctrico es entonces

\[\textbf{E} = - \nabla V = - \frac{4 V_{0}}{d} \sum_{n=1 \\ n \textrm{ odd}}^{\infty} \bigg( - \sin \frac{n \pi y}{d} \textbf{i}_{x} + \cos \frac{n \pi y}{d} \textbf{i}_{y} \bigg) e^{-n \pi x/d} \nonumber \]

Las líneas de campo y equipotenciales se esbozan en la Figura 4-5. Tenga en cuenta que para x >> d, la solución está dominada por el primer armónico. Lejos de ser una fuente, las soluciones laplacianas son insensibles a los detalles de la geometría de origen.

4-2-6 Soluciones tridimensionales

Si el potencial depende de las tres coordenadas (x, y, z), generalizamos nuestro enfoque probando una solución producto de la forma

\[V(x, y, z) = X (x) Y (y) Z (z) \nonumber \]

que, cuando se sustituye en la ecuación de Laplace, rinde después de la división por XYZ

\[\frac{1}{X} \frac{d^{2}X}{dx^{2}} + \frac{1}{Y} \frac{d^{2}Y}{dy^{2}} + \frac{1}{Z} \frac{d^{2}Z}{dz^{2}} = 0 \nonumber \]

tres términos cada uno completamente una función de una sola coordenada de manera que cada término nuevamente debe ser igual por separado a una constante:

\[\frac{1}{X} \frac{d^{2}X}{dx^{2}} = - k^{2}_{x}, \: \: \: \: \frac{1}{Y} \frac{d^{2}Y}{dy^{2}} = -k^{2}_{y}, \: \: \: \: \frac{1}{Z} \frac{d^{2}Z}{dz^{2}} = k_{x}^{2} + k_{y}^{2} \nonumber \]

Cambiamos el signo de la constante de separación para la dependencia z ya que la suma de constantes de separación debe ser cero. Las soluciones para constantes de separación distintas de cero son

\[X = A_{1} \sin k_{x}X + A_{2} \cos k_{x}x} \\ Y = B_{1} \sin k_{y}y + B_{2} \cos k_{y}y \\ Z = C_{1} \sinh k_{z}z + C_{2} \cosh k_{z}z = D_{1} e^{k_{z}z} + D_{2}e^{-k_{z}z} \nonumber \]

Las soluciones se escriben como si k _x, k _y k _z fueran reales para que la dependencia x e y sea trigonométrica mientras que la dependencia z es hiperbólica o equivalentemente exponencial. Sin embargo, k _x, k _y, o k _z pueden ser imaginarios convirtiendo funciones hiperbólicas a trigonométricas y viceversa. Debido a que los cuadrados de las constantes de separación deben sumar a cero al menos una de las soluciones en (38) debe ser trigonométrica y otra debe ser hiperbólica. El resto de la solución puede ser trigonométrica o hiperbólica dependiendo de las condiciones límite. Si las constantes de separación son todas cero, además de las soluciones de (6) tenemos la suma similar

\[Z = e_{1}z + f_{1} \nonumber \]