4.3: Separación de variables en geometría cilíndrica

Soluciones de productos a la ecuación de Laplace en coordenadas cilíndricas

\[\frac{1}{\textrm{r}} \frac{\partial}{\partial \textrm{r}} \bigg( \textrm{r} \frac{\partial V}{\partial r} \bigg) + \frac{1}{\textrm{r}^{2}} \frac{\partial^{2}V}{\partial \phi^{2}} + \frac{\partial^{2}V}{dz^{2}} = 0 \nonumber \]

también se separan en ecuaciones diferenciales ordinarias solucionables.

4-3-1 Soluciones Polar

Si la geometría del sistema no varía con z, intentamos una solución que sea producto de funciones que solo dependen del radio r y el ángulo\(\phi\):

\[V (\textrm{r,} \phi) = \textrm{R}(\textrm{r}) \Phi (\phi) \nonumber \]

que cuando se sustituye en (1) rinde

\[\frac{\Phi}{\textrm{r}} \frac{d}{d \textrm{r}} \bigg( \textrm{r} \frac{d \textrm{R}}{d \textrm{r}} \bigg) + \frac{\textrm{R}}{\textrm{r}^{2}} \frac{d^{2} \Phi}{d \phi^{2}} = 0 \nonumber \]

Esta supuesta solución es conveniente cuando los límites se encuentran en un ángulo constante\(\phi\) o tienen un radio constante, ya que una de las funciones en (2) es entonces constante a lo largo del límite.

Para que (3) se separe, cada término solo debe ser una función de una sola variable, así multiplicamos por r ² /R\(\Phi\) y establecemos cada término igual a una constante, que escribimos como n ²:

\[\frac{\textrm{r}}{\textrm{R}} \frac{d}{d \textrm{r}} \bigg( \textrm{r} \frac{d \textrm{R}}{d \textrm{r}} \bigg) = n^{2}, \: \: \: \: \frac{1}{\Phi} \frac{d^{2} \Phi}{d \phi^{2}} = - n^{2} \nonumber \]

La solución para\(\Phi\) se resuelve fácilmente como

\[\Phi = \left \{ \begin{matrix} A_{1} \sin n \phi + A_{2} \cos n \phi, & n \neq 0 \\ B_{1} \phi + B_{2}, & n = 0 \end{matrix} \right. \nonumber \]

La solución para la dependencia radial no es tan obvia. Sin embargo, si podemos encontrar dos soluciones independientes por cualquier medio, incluida la adivinación, la solución total se da de manera única como una combinación lineal de las dos soluciones. Entonces, probemos una solución de ley de poder de la forma

\[\textrm{R} = A \textrm{r}^{p} \nonumber \]

que cuando se sustituye en (4) rinde

\[p^{2} = n^{2} \Rightarrow p = \pm n \nonumber \]

Para\(n \neq 0\), (7) nos da dos soluciones independientes. Cuando n =0 nos referimos de nuevo a (4) para resolver

\[\textrm{r} \frac{d \textrm{R}}{d \textrm{r}} = \textrm{const} \Rightarrow \textrm{R} = D_{1} \ln \textrm{r} + D_{2} \nonumber \]

para que las soluciones sean

\[\textrm{R} = \left \{ \begin{matrix} C_{1} \textrm{r}^{n} + C_{2} \textrm{r}^{-n}, & n \neq 0 \\ D_{1} \ln \textrm{r} + D_{2}, & n=0 \end{matrix} \right. \nonumber \]

Reconocemos la solución n =0 para la dependencia radial como el potencial debido a una carga de línea. La solución n =0 para la\(\phi\) dependencia muestra que el potencial aumenta linealmente con el ángulo. Generalmente, n puede ser cualquier número complejo, aunque en situaciones habituales donde el dominio es periódico y se extiende por todo el rango\(0 \leq \phi \leq 2 \pi\), el potencial at\(\phi = 2 \pi\) debe ser igual a ese at\(\phi\) = 0 ya que son el mismo punto. Esto requiere que n sea un entero.

Ejemplo 4.3.1

Dos planos de extensión infinita en la dirección z en un ángulo a entre sí, como se muestra en la Figura 4-7, están en una diferencia de potencial v. Los planos no se cruzan sino que se acercan lo suficiente entre sí para que los campos marginales en los extremos de los electrodos puedan descuidarse. Los electrodos se extienden de r = a a r = b. ¿Cuál es la capacitancia aproximada por unidad de longitud de la estructura?

Figura 4-7 Dos planos conductores en ángulo\(\alpha\) tensados por un voltaje v tienen un campo eléctrico\(\phi\) dirigido.

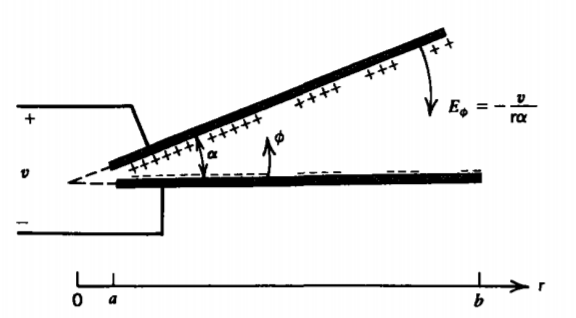
Solución

Intentamos la solución n =0 de (5) sin dependencia radial como

\(V = B_{1} \phi + B_{2}\)

Las condiciones de contorno imponen las restricciones

\(V(\phi = 0) = 0, \: \: \: \: V(\phi = \alpha) = v \Rightarrow V = v \phi / \alpha\)

El campo eléctrico es

\(E_{\phi} = - \frac{1}{\textrm{r}} \frac{dV}{d \phi} = - \frac{v}{\textrm{r} \alpha} \)

La densidad de carga superficial en el electrodo superior es entonces

\(\sigma_{f} (\phi = \alpha) = - \varepsilon E_{\phi} (\phi = \alpha) = \frac{\varepsilon v}{\textrm{r} \alpha}\)

con carga total por unidad de longitud

\(\lambda (\phi = \alpha) = \int_{\textrm{r} =a}^{b} \sigma_{f} (\phi = \alpha) d \textrm{r} = \frac{\varepsilon v}{\alpha} \ln \frac{b}{a}\)

para que la capacitancia por unidad de longitud sea

\(C = \frac{\lambda}{v} = \frac{\varepsilon \: \ln (b/a)}{\alpha}\)

4-3-2 Cilindro en un Campo Eléctrico Uniforme

(a) Soluciones de campo

Un cilindro infinitamente largo de radio a, permitividad\(\varepsilon_{2}\) y conductividad óhmica\(\sigma_{2}\) se coloca dentro de un medio infinito de permitividad\(\varepsilon_{1}\) y conductividad\(\sigma_{1}\). Un campo eléctrico uniforme al infinito\(\textbf{E} = E_{0} \textbf{i}_{x}\), se enciende repentinamente a t =0. Este problema es análogo al condensador con pérdidas en serie tratado en la Sección 3-6-3. Al igual que allí, encontraremos de manera similar que:

(i) A t = 0 la solución es la misma que para dos dieléctricos sin pérdidas, independientes de las conductividades, sin carga superficial interfacial, descrita por la condición límite

\[\sigma_{f} (\textrm{r} = a) = D_{\textrm{r}} (\textrm{r} = a_{+}) - D_{\textrm{r}}(\textrm{r} = a_{-}) = 0 \\ \Rightarrow \varepsilon_{1} E_{\textrm{r}}(\textrm{r} = a_{+}) = \varepsilon_{2}E_{\textrm{r}}(\textrm{r} = a_{-}) \nonumber \]

ii) Como\(t \rightarrow \infty\), la solución de estado estacionario depende únicamente de las conductividades, con continuidad de corriente normal en la interfaz del cilindro,

\[J_{\textrm{r}}(\textrm{r} = a_{+}) = J_{\textrm{r}}(\textrm{r} = a_{-}) \Rightarrow \sigma_{1} E_{\textrm{r}}(\textrm{r} = a_{+}) = \sigma_{2} E_{\textrm{r}}(\textrm{r} = a_{-}) \nonumber \]

(iii) La constante de tiempo que describe la transición de las soluciones iniciales a las soluciones de estado estacionario dependerá de algún promedio ponderado de la relación de permitividades a conductividades.

Para resolver el problema transitorio general debemos encontrar el potencial tanto dentro como fuera del cilindro, uniendo las soluciones en cada región a través de las condiciones límite en r = a.

Probando las soluciones distintas de cero n de (5) y (9), n debe ser un entero como el potencial en\(\phi = 0\) y\(\phi = 2 \pi\) debe ser igual, ya que son el mismo punto. Para el caso más general, es necesaria una serie infinita de términos, superponiendo soluciones con n = 1, 2, 3, 4,... Sin embargo, debido a la forma del campo eléctrico uniforme aplicado al infinito, expresado en coordenadas cilíndricas como

\[\textbf{E} (\textrm{r} \rightarrow \infty) = E_{0} \textbf{i}_{x} = E_{0}[\textbf{i}_{\textrm{r}} \cos \phi - \textbf{i}_{\phi} \sin \phi] \nonumber \]

podemos cumplir todas las condiciones de contorno usando solo la solución n = 1.

Manteniendo la solución finita a r =0, intentamos soluciones de la forma

\[V(\textrm{r}, \phi) = \left \{ \begin{matrix} A(t) \textrm{r} \cos \phi, & \textrm{r} \leq a \\ [B(t) \textrm{r} + C(t)/ \textrm{r}] \cos \phi, & r \geq a \end{matrix} \right. \nonumber \]

con campo eléctrico asociado

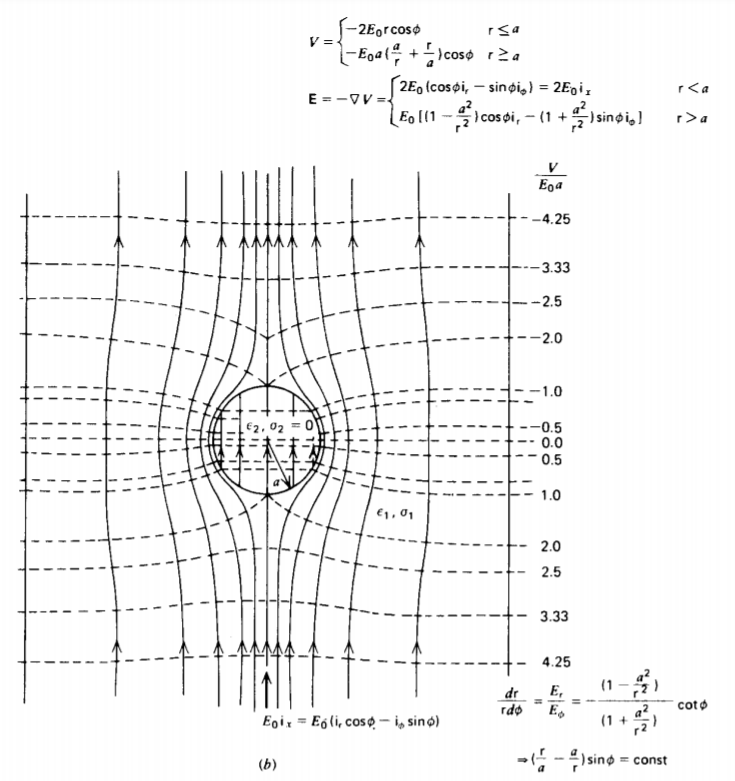
\[\textbf{E} = - \nabla V = \left \{ \begin{matrix} -A (t) [ \cos \phi \textbf{i}_{r} - \sin \phi \textbf{i}_{\phi}] = - A(t) \textbf{i}_{x}, & \textrm{r} < \textrm{a} \\ - [\textbf{B}(t) - C(t)/ \textrm{r}^{2}] \cos \phi \textbf{i}_{\textrm{r}} \\ + [B(t) + C(t)/ \textrm{r}^{2}] \sin \phi \textbf{i}_{\phi}, & \textrm{r} > \textrm{a} \end{matrix} \right. \nonumber \]

No consideramos la\(\phi\) solución al pecado de (5) en (13) porque al infinito el campo eléctrico tendría que ser y dirigido:

\[V = D \textrm{r} \sin \phi \Rightarrow \textbf{E} = - \nabla V = - D [ \textbf{i}_{\textrm{r}} \sin \phi + \textbf{i}_{\phi} \cos \phi ] = -D \textbf{i}_{y} \nonumber \]

El campo eléctrico dentro del cilindro es x dirigido. La solución exterior se debe en parte al campo uniforme impuesto x -dirigido, de manera que como r\(\rightarrow \infty\) el campo de (14) debe acercarse a (12), requiriendo que\(B(t) = E_{0}\). La contribución restante al campo externo es equivalente a un dipolo lineal bidimensional (ver Problema 3.1), con momento dipolar por unidad de longitud:

\[p_{x} = \lambda d = 2 \pi \varepsilon C (t) \nonumber \]

Las otras amplitudes dependientes del tiempo A (t) y C (t) se encuentran a partir de las siguientes condiciones límite adicionales:

(i) el potencial es continuo a r= a, lo que es lo mismo que requerir continuidad del componente tangencial de E:

\[V(\textrm{r} = a_{+}) = V(\textrm{r} = a_{-}) \Rightarrow E_{\phi}(\textrm{r} = a_{-}) = E_{\phi} (\textrm{r} = a_{+}) \\ \Rightarrow Aa = Ba + C/a \nonumber \]

(ii) la carga debe conservarse en la interfaz

\[J_{\textrm{r}} (\textrm{r} = a_{+}) - J_{\textrm{r}}(\textrm{r} = a_{-}) + \frac{\partial \sigma_{f}}{\partial t} = - \\ \Rightarrow \sigma_{1} E_{\textrm{r}} (\textrm{r} = a_{+}) - \sigma_{2} E_{\textrm{r}}(\textrm{r} = a_{-}) \\ + \frac{\partial}{\partial t} [ \varepsilon_{1} E_{\textrm{r}}(\textrm{r} = a_{+}) - \varepsilon_{2} E_{\textrm{r}}(\textrm{r} = a_{-})]= 0 \nonumber \]

En el estado estacionario, (18) se reduce a (11) para la continuidad de la corriente normal, mientras que para t =0 la derivada de tiempo debe ser no infinita por lo que\(\sigma_{f}\) es continua y por lo tanto cero como lo da (10).

Usando (17) en (18) obtenemos una sola ecuación en C (t):

\[\frac{dC}{dt} + \bigg( \frac{\sigma_{1} + \sigma_{2}}{\varepsilon_{1} + \varepsilon_{2}}\bigg) C = \frac{-a^{2}}{\varepsilon_{1} + \varepsilon_{2}} \bigg( E_{0} (\sigma_{1} - \sigma_{2}) + ( \varepsilon_{1} - \varepsilon_{2}) \frac{dE_{0}}{dt} \bigg) \nonumber \]

Dado que\(E_{0}\) es una función de paso en el tiempo, el último término en el lado derecho es una función de impulso, que impone la condición inicial

\[C(t=0) = -a^{2} \frac{(\varepsilon_{1} - \varepsilon_{2})}{\varepsilon_{1} + \varepsilon_{2}}E_{0} \nonumber \]

de manera que la solución total a (19) es

\[C(t) = a^{2}E_{0} \bigg( \frac{\sigma_{1} - \sigma_{2}}{\sigma_{1} + \sigma_{2}} + \frac{2 (\sigma_{1} \varepsilon_{2} - \sigma_{2} \varepsilon_{1})}{(\sigma_{1} + \sigma_{2}) (\varepsilon_{1} + \varepsilon_{2})} e^{-t/\tau}\bigg), \: \: \: \tau = \frac{\varepsilon_{1} + \varepsilon_{2}}{\sigma_{1} + \sigma_{2}} \nonumber \]

La carga superficial interfacial es

\[\sigma_{f} (\textrm{r} = \textrm{a}, t) = \varepsilon_{1} E_{\textrm{r}}(\textrm{r} = \textrm{a}_{+}) - \varepsilon_{2} E_{\textrm{r}}(\textrm{r} = a_{-}) \\ = \bigg[ - \varepsilon_{1} \bigg( B = \frac{C}{a^{2}}\bigg) + \varepsilon_{2}A \bigg] \cos \phi \\ = \bigg[ (\varepsilon_{1} = \varepsilon_{2}) E_{0} + (\varepsilon_{1} + \varepsilon_{2}) \frac{C}{a^{2}} \bigg] \cos \phi \\ = \frac{2 (\sigma_{2} \varepsilon_{1} - \sigma_{1} \varepsilon_{2})}{\sigma_{1} + \sigma_{2}} E_{0}[1 - e^{-t/\tau}] \cos \phi \nonumber \]

La parte superior del cilindro (\(- \pi/2 \leq \phi \leq \pi/2) is charged of one sign while the lower half (\(\pi/2 \leq \phi \leq \frac{3}{2} \pi\)) se carga con el signo opuesto, siendo cero la carga neta en el cilindro. El cilindro se descarga en cada punto de su superficie si los tiempos de relajación en cada medio son los mismos,\(\varepsilon_{1}/\sigma_{1} = \varepsilon_{2}/\sigma_{2}\)

La solución para el campo eléctrico a t =0 es

\[\textbf{E} (t = 0) = \left \{ \begin{matrix} \frac{2 \varepsilon_{1} E_{0}}{\varepsilon_{1} + \varepsilon_{2}} [\cos \phi \textbf{i}_{\textrm{r}} - \sin \phi \textbf{i}_{\phi}] = \frac{2 \varepsilon_{1} E_{0}}{\varepsilon_{1} + \varepsilon_{2}} \textbf{i}_{x}, & \textrm{r} < a\\ E_{0} \bigg[ \bigg( 1 + \frac{a^{2}}{\textrm{r}^{2}} \frac{\varepsilon_{2} - \varepsilon_{1}}{\varepsilon_{1} + \varepsilon_{2}} \bigg) \cos \phi \textbf{i}_{\textrm{r}} \\ - \bigg(1 - \frac{a^{2}}{\textrm{r}^{2}} \frac{\varepsilon_{2} - \varepsilon_{1}}{\varepsilon_{1} + \varepsilon_{2}} \bigg) \sin \phi \textbf{i}_{\phi} \bigg], & \textrm{r} >a \end{matrix} \right. \nonumber \]

El campo dentro del cilindro está en la misma dirección que el campo aplicado, y se reduce en amplitud si\(\varepsilon_{2} > \varepsilon_{1}\) y aumenta en amplitud si\(\varepsilon_{2} < \varepsilon_{1}\), hasta un factor limitante de dos como\(\varepsilon_{1}\) se vuelve grande en comparación con\(\varepsilon_{2}\). Si\(\varepsilon_{2} - \varepsilon_{1}\), la solución se reduce al campo aplicado uniforme en todas partes.

La solución de estado estacionario dc es idéntica en forma a (23) si reemplazamos las permitividades en cada región por sus conductividades;

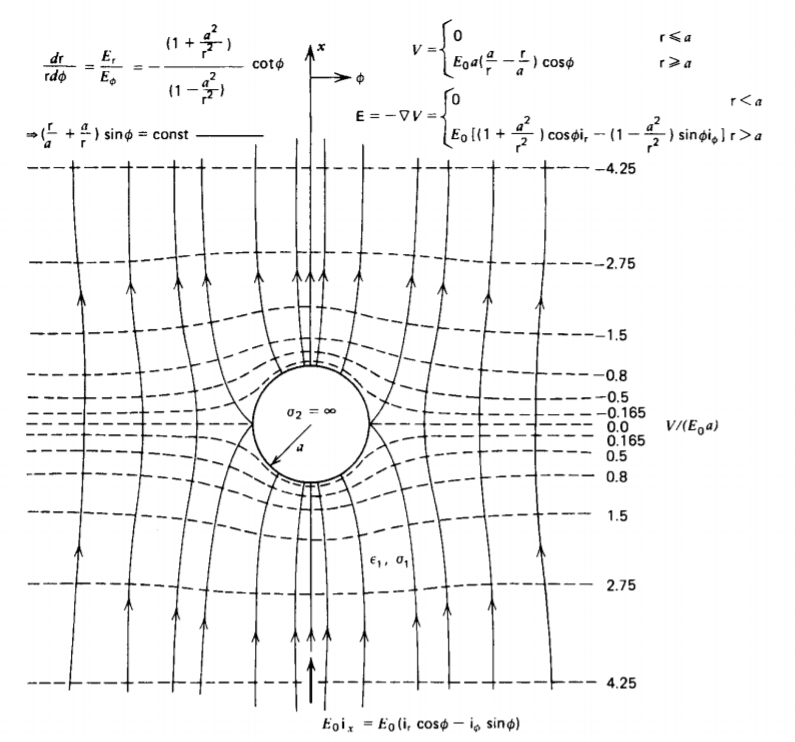
\[\textbf{E} (t \rightarrow \infty) = \left \{ \begin{matrix} \frac{2 \sigma_{1} E_{0}}{\sigma_{1} + \sigma_{2}} [\cos \phi \textbf{i}_{\textrm{r} - \sin \phi \textbf{i}_{\phi}] = \frac{2 \sigma_{1} E_{0}}{\sigma_{1} + \sigma_{2}} \textbf{i}_{x}, & \textrm{r} < a \\ E_{0} \bigg[ \bigg( 1 + \frac{a^{2}}{\textrm{r}^{2}} \frac{\sigma_{2} - \sigma_{1}}{\sigma_{1} + \sigma_{2}} \bigg) \cos \phi \textbf{i}_{\textrm{r}} \\ - \bigg( 1 - \frac{a^{2}}{\textrm{r}^{2}} \frac{\sigma_{2} - \sigma_{1}}{\sigma_{1} + \sigma_{2} \bigg) \sin \phi \textbf{i}_{\phi} \bigg], & \textrm{r} > a \end{matrix} \right. \nonumber \]

(b) Trazado de líneas de campo

Debido a que la región fuera del cilindro es libre de cargos, eso lo sabemos\(\nabla \cdot \textbf{E} = 0 \). De la identidad derivada en la Sección 1-5-4b, que la divergencia del rizo de un vector es cero, sabemos así que el campo eléctrico polar sin componente z puede expresarse en la forma

\[\textbf{E} (\textrm{r}, \phi) = \nabla \times \Sigma (\textrm{r}, \phi) \textbf{i}_{z} \\ = \frac{1}{\textrm{r}} \frac{\partial \Sigma}{\partial \phi} \textbf{i}_{\textrm{r}} - \frac{\partial \Sigma}{\partial \textrm{r}} \textbf{i}_{\phi} \nonumber \]

donde\(\Sigma\) se llama la función de flujo. Tenga en cuenta que el vector de función stream está en la dirección perpendicular al campo eléctrico de manera que su curl tiene componentes en la misma dirección que el campo.

A lo largo de una línea de campo, que siempre es perpendicular a las líneas equipotenciales,

\[\frac{d \textrm{r}}{\textrm{r} d \phi} = \frac{E_{\textrm{r}}}{E_{\phi}} = - \frac{1}{\textrm{r}} \frac{\partial \Sigma /\partial \phi}{\partial \Sigma/ \partial \textrm{r}} \nonumber \]

Al multiplicar y agrupar términos cruzados en un lado de la ecuación, (26) reduce a

\[d \Sigma = \frac{\partial \Sigma}{\partial \textrm{r}}d \textrm{r} + \frac{\partial \Sigma}{\partial \phi} d \phi = 0 \Rightarrow \sigma = \textrm{const} \nonumber \]

Las líneas de campo son así líneas de constante\(\Sigma\).

Para la solución de estado estacionario de (24), fuera del cilindro

\[\frac{1}{\textrm{r}} \frac{\partial \Sigma}{\partial \phi} = E_{\textrm{r}} = \E_{0} \bigg( 1 + \frac{a^{2}} {\textrm{r}^{2}} \frac{\sigma_{2} - \sigma_[1}}{\sigma_{1} + \sigma_{2}} \bigg) \cos \phi \\ - \frac{\partial \Sigma}{\partial \textrm{r}} = E_{\phi} = - E_{0} \bigg( 1 - \frac{a^{2}}{\textrm{r}^{2}} \frac{\sigma_{2} - \sigma_{1}}{\sigma_{1} + \sigma_{2}} \bigg) \sin \phi \nonumber \]

encontramos por integración que

\[\sigma = E_{0} \bigg( \textrm{r} + \frac{a^{2}}{\textrm{r}} \frac{\sigma_{2} - \sigma_{1}}{\sigma_{1} + \sigma_{2}} \bigg) \sin \phi \nonumber \]

El campo de estado estacionario y las líneas equipotenciales se dibujan en la Figura 4-8 cuando el cilindro está perfectamente conductor (\(\sigma_{2} \rightarrow x \)) o perfectamente aislante (\(\sigma_{2}\)= 0).

Si el cilindro es altamente conductor, el campo eléctrico interno es cero con el campo eléctrico externo incidente radialmente, como se dibuja en la Figura 4-8a. En contraste, cuando el cilindro es perfectamente aislante, las líneas de campo externas deben ser puramente tangenciales al cilindro ya que la corriente normal incidente es cero, y el campo eléctrico interno tiene el doble de intensidad del campo aplicado, como se dibuja en la Figura 4-8b.

4-3-3 Soluciones tridimensionales

Si el potencial eléctrico depende de las tres coordenadas, intentamos una solución de producto de la forma

\[V( \textrm{r}, \phi , z) = \textrm{R}(\textrm{r}) \Phi (\phi) Z (z) \nonumber \]

que cuando se sustituye en la ecuación de Laplace rinde

\[\frac{Z \Phi}{\textrm{r}} \frac{d}{d \textrm{r}} \bigg( \textrm{r} \frac{d \textrm{R}}{d \textrm{r}} + \frac{\textrm{R} Z}{\textrm^{2}} \frac{d^{2} \Phi}{d \phi^{2}} + \textrm{R} \Phi \frac{d^{2} Z}{d z^{2}} = 0 \nonumber \]

Ahora tenemos una dificultad, ya que no podemos dividirnos por un factor para hacer de cada término una función sólo de una sola variable.

Figura 4-8 Campo de estado estacionario y líneas equipotenciales alrededor de un (a) cilindro perfectamente conductor o (b) perfectamente aislante en un campo eléctrico uniforme.

Sin embargo, dividiendo por\(V = \textrm{R} \Phi Z\)

\[\underbrace{ \frac{1}{\textrm{Rr}} \frac{d}{d \textrm{r}} \bigg( \textrm{r} \frac{d \textrm{R}}{d \textrm{r} \bigg) + \frac{1}{\textrm^{2} \Phi} \frac{d^{2} \Phi}{d \phi^{2}}}_{-k^{2}} + \underbrace{\frac{1}{Z} \frac{d^{2}Z}{dz^{2}}}_{k^{2}} = 0 \nonumber \]

vemos que los dos primeros términos son funciones de r y\(\phi\) mientras que el último término es sólo una función de z. Por lo tanto, este último término debe ser igual a una constante:

\[\frac{1}{Z} \frac{d^{2}Z}{dz^{2}} = k^{2} \Rightarrow Z = \left \{ \begin{matrix} A_{1} \sinh kz + A_{2} \cosh kz, & k \neq 0 \\ A_{3}z + A_{4}, & k = 0 \end{matrix} \right. \nonumber \]

Figura 4-8b

Los dos primeros términos en (32) ahora deben sumar a - k ² de manera que después de multiplicar por r ² tengamos

\[\frac{\textrm{r}}{\textrm{R}} \frac{d}{d \textrm{r}} \bigg( \textrm{r} \frac{d \textrm{R}}{d \textrm{r} \bigg) + k^{2} \textrm{r}^{2} + \frac{1}{\Phi} \frac{d^{2} \Phi}{d \phi^{2}} = 0 \nonumber \]

Ahora de nuevo los dos primeros términos son solo una función de r, mientras que el último término es sólo una función de\(\phi\) así que (34) vuelve a separar:

\[\frac{\textrm{r}}{\textrm{R}} \frac{d}{d \textrm{r}} \bigg( \textrm{r} \frac{d \textrm{R}}{d \textrm{r}} \bigg) + k^{2} \textrm{r}^{2} = n^{2}, \: \: \: \: \frac{1}{\Phi} \frac{d^{2} \Phi}{d \phi^{2}} = - n^{2} \nonumber \]

de funciones tabuladas:

\[\textrm{R} = \left \{ \begin{matrix} C_{1}J_{n}(k \textrm{r}) + C_{2} Y_{n}(k \textrm{r}, & k \neq 0 \\ C_{3}\textrm{r}^{n} + C_{4} \textrm{r}^{-n}, & k = 0, \: \: \: \: n \neq 0 \\ C_{5} \ln \textrm{r} + C_{6}, & k= 0, \: \: \: \: n = 0 \end{matrix} \right. \nonumber \]

donde J _n se llama una función de Bessel del primer tipo de orden n e Y _n se llama la función de Bessel de orden n del segundo tipo. Cuando n = 0, las funciones de Bessel son de orden cero mientras que si k =0 las soluciones se reducen a las soluciones bidimensionales de (9).

Algunas de las propiedades y valores limitantes de las funciones de Bessel se ilustran en la Figura 4-9. Recuerda que k

Figura 4-9b

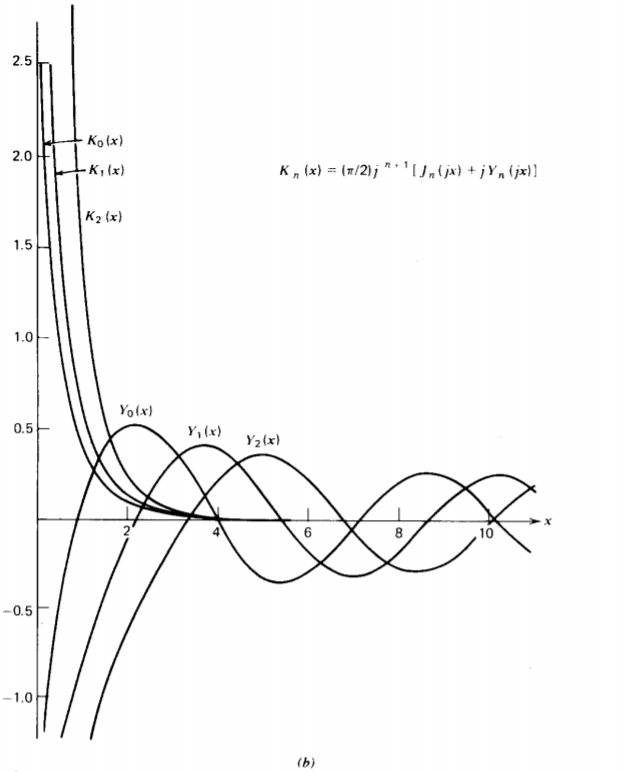
también puede ser puramente imaginario así como real. Cuando k es real para que la dependencia z sea hiperbólica o equivalentemente exponencial, las funciones de Bessel son oscilatorias mientras que si k es imaginaria para que la dependencia axial de z sea trigonométrica, es conveniente definir el Bessel modificado no oscilatorio funciona como

\[I_{n} (k \textrm{r} ) = j^{-n} J_{n}(jk \textrm{r}) \\ K_{n}(k \textrm{r}) = \frac{\pi}{2} j^{n + 1} [J_{n}(jk \textrm{r}) + j Y_{n} )jk \textrm{r})] \nonumber \]

Al igual que en las coordenadas rectangulares, si la solución a la ecuación de Laplace decae en una dirección, es oscilatoria en la dirección perpendicular.

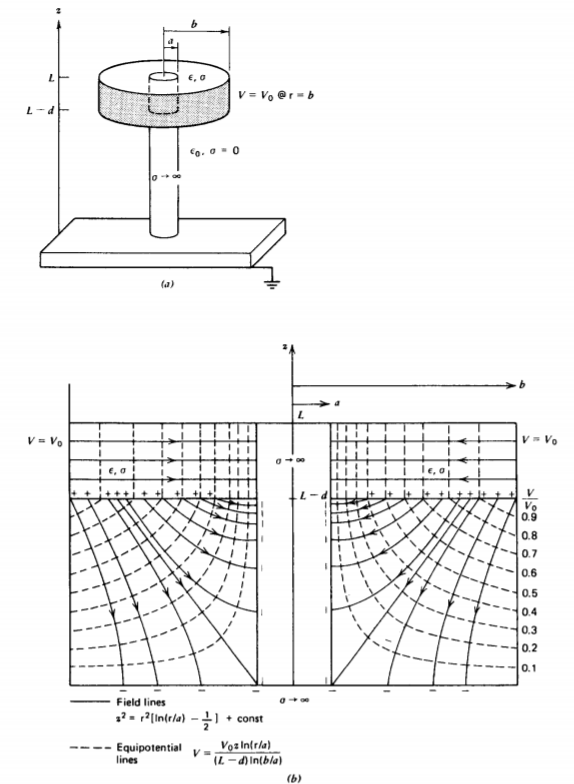
4-3-4 Buje Aislador de Alto Voltaje

El aislante de alto voltaje mostrado en la Figura 4-10 consiste en un disco cilíndrico con conductividad óhmica\(\sigma\) soportado por un poste cilíndrico perfectamente conductor sobre un plano de tierra. *

El plano en z = 0 y el poste en r = a están a potencial cero, mientras que se impone un potencial constante a lo largo de la circunferencia del disco a r = b. La región debajo del disco es espacio libre para que ninguna corriente pueda cruzar las superficies en z = L y z = L - d. Debido a que los límites se encuentran a lo largo de las superficies a la constante z o constante r, probamos las soluciones simples de la constante de separación cero en (33) y (38), que son independientes del ángulo\(\phi\):

\[V(\textrm{r}, z) = \left \{ \begin{matrix} A_{1}z = D_{1}z \: \ln \: \textrm{r} + C_{1} \: \ln \textrm{r} + D_{1}, & L - D < z < L \\ A_{2}z + B_{2} z \: \ln \: \textrm{r} + C_{2} \: \ln \: \textrm{r} + D_{2}, & 0 \leq z \leq L -d \end{matrix} \right. \nonumber \]

Aplicando las condiciones de contorno relacionamos los coeficientes como

\[V(z=0) = 0 \Rightarrow C_{2} = D_{2} = 0 \\ V(\textrm{r} = a) = 0 \Rightarrow \left \{ \begin{matrix} A_{2} + B_{2} \ln \: a = 0 \\ A_{1} + B_{2} \ln \: a = 0 \\ C_{1} \ln \: a + D_{1} = 0 \end{matrix} \right. \\ V(\textrm{r} = b, z > L - d) = V_{0} \Rightarrow \left \{ \begin{matrix} A_{1} + B_{1} \ln \: b = 0 \\ C_{1} \ln \: b + D_{1} = V_{0} \end{matrix} \right. \\ V(z = (L-d)_{-}) = V(z = (L-d)_{+}) \Rightarrow (L-d) (A_{2} + B_{2} \ln \: \textrm{r} ) \\ = (L-d)(A_{1} + B_{1} \ln \: \textrm{r}) + C_{1} \ln \: \textrm{r} + D_{1} \nonumber \]

Figura 4-10 (a) Un disco finitamente conductor se monta sobre un poste cilíndrico perfectamente conductor y se coloca en un plano de tierra perfectamente conductor. b) Líneas de campo y equipotenciales

que arroja los valores

\[A_{1} = B_{1} = 0, \: \: \: \: C_{1} = \frac{V_{0}}{\ln (b/a)}, \: \: \: \: D_{1} = - \frac{V_{0} \ln a}{\ln (b/a)} \\ A_{2} = - \frac{V_{0} \ln a}{(L-d) \ln (b/a)}, \: \: \: \: B_{2} = \frac{V_{0}}{(L-d) \ln (b/a)}, \: \: \: \: C_{2} = D_{2} = 0 \nonumber \]

El potencial de (40) es entonces

\[V(\textrm{r} , z) = \left \{ \begin{matrix} \frac{V_{0} \ln (\textrm{r}/a)}{\ln (b/a)}, & L-d \leq z \leq L \\ \frac{V_{0}z \ln (\textrm{r}/a)}{(L-d) \ln (b/a)}, & 0 \leq z \leq L-d} \end{matrix} \right. \nonumber \]

con campo eléctrico asociado

\[\textbf{E} = - \nabla V = \left \{ \begin{matrix} - \frac{V_{0}}{\textrm{r} \ln (b/a)} \textbf{{i}_{\textrm{r}}, & L - d < Z < L \\ - \frac{V_{0}}{(L-d) \ln (b/a)} \bigg( \ln \frac{\textrm{r}}{a} \textbf{i}_{z} + \frac{z}{\textrm{r}} \textbf{i}_{\textrm{r}} \ bigg), & 0 < z < L -d \end{matrix} \right. \nonumber \]

Las líneas de campo en la región de espacio libre son

\[\frac{d \textrm{r}}{dz} = \frac{E_{\textrm{r}}}{E_{z}} = \frac{z}{\textrm{r} \ln (\textrm{r}/a)} \Rightarrow z^{2} = \textrm{r}^{2} \bigg[ \ln \frac{\textrm{r}}{a} - \frac{1}{2} \bigg] + \textrm{const} \nonumber \]

y se trazan con las líneas equipotenciales en la Figura 4-10b.

* M. N. Horenstein, “Contaminación por partículas de aisladores de CC de alto voltaje”, tesis doctoral, Instituto Tecnológico de Massachusetts, 1978.