5.7: Problemas de valor de límite de campo magnético

5-7-1 El método de las imágenes

Una corriente de línea I de extensión infinita en la dirección z es una distancia d por encima de un plano que es perfectamente conductor o infinitamente permeable, como se muestra en la Figura 5-24. Para ambos casos

Figura 5-24 (a) Una corriente de línea por encima de un conductor perfecto induce una corriente superficial dirigida de manera opuesta que es equivalente a una corriente de línea de imagen ubicada simétricamente. (b) El campo debido a una corriente de línea por encima de un medio infinitamente permeable es el mismo que si el medio fuera reemplazado por una corriente de imagen ahora en la misma dirección que la corriente de línea original.

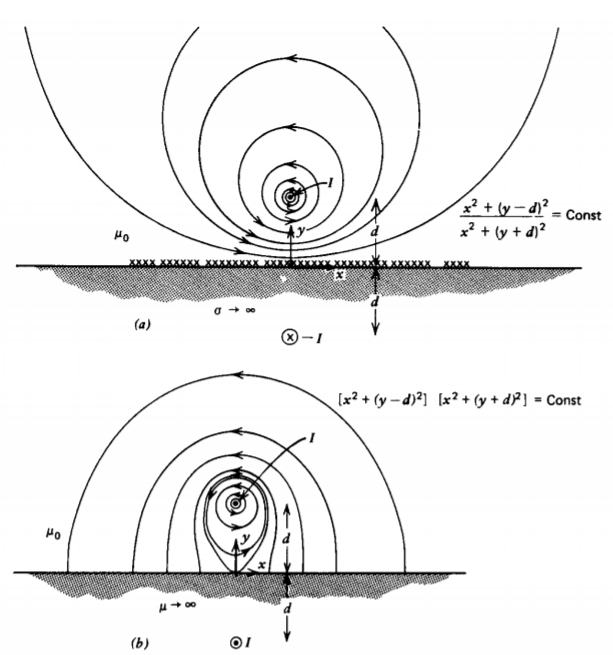
el campo H dentro del material debe ser cero pero las condiciones de contorno en la interfaz son diferentes. En el conductor perfecto tanto B como H deben ser cero, de manera que en la interfaz el componente normal de B y por lo tanto H debe ser continuo y por lo tanto cero. El componente tangencial de H es discontinuo en una corriente superficial.

En el material infinitamente permeable H es cero pero B es finito. Ninguna corriente superficial puede fluir porque el material no es un conductor, por lo que el componente tangencial de H es continuo y por lo tanto cero. El campo B debe ser normalmente incidente.

Ambos conjuntos de condiciones límite se pueden cumplir colocando una corriente de imagen I en y = - d que fluye en la dirección opuesta para el conductor y en la misma dirección para el material permeable.

Usando el signo superior para el conductor y el signo inferior para el material infinitamente permeable, el potencial vectorial debido a ambas corrientes se encuentra superponiendo el potencial vectorial encontrado en la Sección 5-4-3a, Ec. (18), para cada corriente de línea infinitamente larga:

\[A_{z} = \frac{-\mu_{0}I}{2 \pi} (\ln [ x^{2} + (y-d)^{2}]^{1/2} \mp \ln[x^{2} + (y + d)^{2}]^{1/2}) \\ = \frac{- \mu_{0}I}{4 \pi} (\ln [x^{2} + (y-d)^{2}] \mp \ln [x^{2} + (y + d)^{2}]) \nonumber \]

con campo magnético resultante

\[\textbf{H} = \frac{1}{\mu_{0}} \nabla \times \textbf{A} = \frac{1}{\mu_{0}} \bigg(\textbf{i}_{x} \frac{\partial A_{z}}{\partial y} - \textbf{i}_{y} \frac{\partial A_{z}}{\partial x} \bigg) = \frac{-I}{2 \pi} \left \{ \begin{matrix} \frac{(y-d) \textbf{i}_{x} - x \textbf{i}_{y}}{[x^{2} + (y-d)^{2}]} \mp \frac{(y + d) \textbf{i}_{x} - x \textbf{i}_{y}}{[x^{2} + (y + d)^{2}]} \end{matrix} \right. \nonumber \]

La distribución de corriente superficial para el caso conductor viene dada por la discontinuidad en H tangencial,

\[K_{z} = - H_{x} (y=0) = - \frac{Id}{\pi[d^{2} + x^{2}]} \nonumber \]

que tiene corriente total

\[I_{T} = \int_{-\infty}^{+\infty} K_{z} dx = - \frac{Id}{\pi} \int_{- \infty^{+ \infty} \frac{dx}{(x^{2} + d^{2}) \\ = - \frac{Id}{\pi} \frac{1}{d} \tan^{-1} \frac{x}{d} \bigg|_{- \infty}^{+ \infty} = = I \nonumber \]

igual a la corriente de imagen.

La fuerza por unidad de longitud sobre la corriente para cada caso se debe solo al campo magnético de su imagen:

\[\textbf{f} = \pm \frac{\mu_{0}I^{2}}{4 \pi d} \textbf{i}_{y} \nonumber \]

siendo repulsivo para el conductor y atractivo para el material permeable.

Las líneas de campo magnético trazadas en la Figura 5-24 son solo líneas de constante\(A_{z}\) como se deriva en la Sección 5-4-3b. Justo al lado de la línea actual domina el término de campo propio y las líneas de campo son círculos. El campo lejano en la Figura 5-24b, cuando la corriente de línea e imagen están en la misma dirección, es el mismo que si tuviéramos una corriente de línea única de 2 I.

5-7-2 Esfera en un Campo Magnético Uniforme

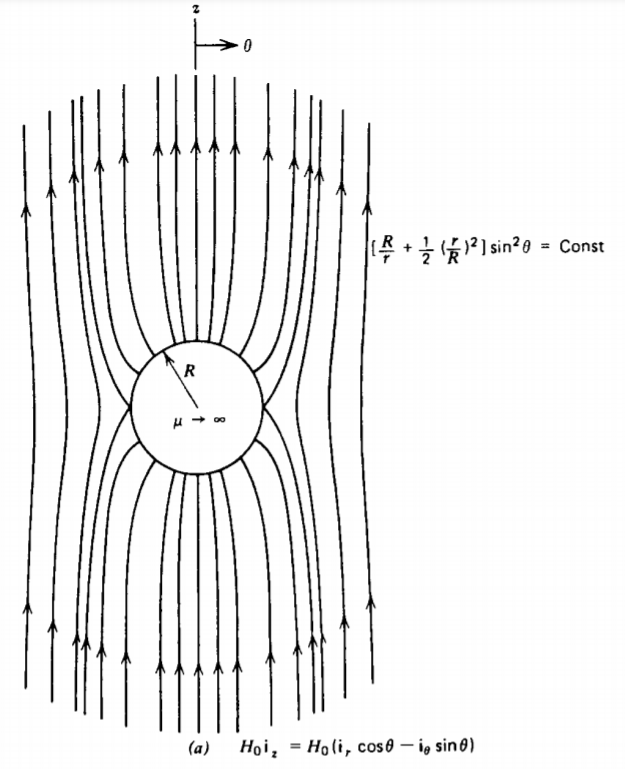
Una esfera de radio R se coloca dentro de un campo magnético uniforme\(H_{0} \textbf{i}_{z}\). La esfera y el medio circundante pueden tener cualquiera de las siguientes propiedades ilustradas en la Figura 5-25:

1. La esfera tiene permeabilidad\(\mu_{2}\) y el medio circundante tiene permeabilidad\(\mu_{1}\).
2. Esfera perfectamente conductora en el espacio libre.
3. Esfera uniformemente magnetizada\(M_{2} \textbf{i}_{z}\), en un medio uniformemente magnetizado\(M_{1}\textbf{i}_{z}\).

Para cada uno de estos tres casos, no hay corrientes libres en ninguna de las regiones por lo que las ecuaciones gobernantes en cada región son

\[\nabla \cdot \textbf{B} = 0 \\ \nabla \times \textbf{H} = 0 \nonumber \]

Figura 5-25 Líneas de campo magnético alrededor de una (a) esfera infinitamente permeable y (b) perfectamente conductora en un campo magnético uniforme.

Figura 5-25

Debido a que el rizo de H es cero, podemos definir un potencial magnético escalar

\[\textbf{H} = \nabla_{\chi} \nonumber \]

donde evitamos el uso de un signo negativo como se usa con el campo eléctrico ya que el potencial sólo\(\chi\) se introduce como una conveniencia matemática y no tiene significación física. Con B proporcional a H o para magnetización uniforme, la divergencia de H también es cero de manera que el potencial magnético escalar obedece a la ecuación de Laplace en cada región:

\[\nabla^{2}_{\chi} = 0 \nonumber \]

Luego podemos usar las mismas técnicas desarrolladas para el campo eléctrico en la Sección 4-4 probando un potencial escalar en cada región como

\[\chi = \left \{ \begin{matrix} Ar \cos \theta, & r< R \\ (Dr + C/r^{2}) \cos \theta & r > R \end{matrix} \right. \nonumber \]

El campo magnético asociado es entonces

\[\textbf{H} = \nabla_{\chi} = \frac{\partial \chi}{\partial r} \textbf{i}_{r} + \frac{1}{r} \frac{\partial \chi}{\partial \theta} \textbf{i}_{\theta} + \frac{1}{r \sin \theta} \frac{\partial_{\chi}}{\partial \phi} \textbf{i}_{\phi} \\ = \left \{ \begin{matrix} A(\textbf{i}_{r} \cos \theta - \textbf{i}_{\theta} \sin \theta) = A \textbf{i}_{z}, & r< R \\ (D - 2C/r^{3}) \cos \theta \textbf{i}_{r} - (D + C/r^{3}) \sin \theta \textbf{i}_{\theta}, & r > R \end{matrix} \right. \nonumber \]

Para los tres casos, el campo magnético lejos de la esfera debe acercarse al campo aplicado uniforme:

\[\textbf{H}(r = \infty) = H_{0} \textbf{i}_{z} = H_{0}(\textbf{i}_{r} \cos \theta - \textbf{i}_{theta} \sin \theta) \Rightarrow D = H_{0} \nonumber \]

Las otras constantes, A y C, se encuentran a partir de las condiciones de contorno a r = R. El campo dentro de la esfera es uniforme, en la misma dirección que el campo aplicado. La solución fuera de la esfera es el campo impuesto más una contribución como si hubiera un dipolo magnético en el centro de la esfera con el momento\(m_{z} = 4 \pi C\).

(i) Si la esfera tiene una permeabilidad diferente de la región circundante, tanto los componentes tangenciales de H como los componentes normales de B son continuos a través de la superficie esférica:

\[H_{\theta} (r = R_{+}) = H_{\theta}(r = R_{-}) \Rightarrow A = D + C/R^{3} \\ B_{r} (r = R_{+}) = B_{r} (r = R_{-}) \Rightarrow \mu_{1} H_{r}(r = R_{+}) = \mu_{2}H_{r}(r=R_{-}) \nonumber \]

lo que produce soluciones

\[A = \frac{3 \mu_{1}H_{0}}{\mu_{2} + 2 \mu_{1}}, \: \: \: \: C = - \frac{\mu_{2}-\mu_{1}}{\mu_{2} + 2 \mu_{1}} R^{3} H_{0} \nonumber \]

La distribución del campo magnético es entonces

\[\textbf{H} = \left \{ \begin{matrix} \frac{3 \mu_{1}H_{0}}{\mu_{2} + 2 \mu_{1}} (\textbf{i}_{r} \cos \theta - \textbf{i}_{\theta} \sin \theta) = \frac{3 \mu_{1}H_{0} \textbf{i}_{z}}{\mu_{2} + 2 \mu_{1}}, & r < R \\ H_{0} \left \{ \bigg[ 1 + \frac{2R^{3}}{r^{3}} \bigg( \frac{\mu_{2}- \mu_{1}}{\mu_{2} + 2 \mu_{1}} \bigg) \bigg] \cos \theta \textbf{i}_{r} \\ - \bigg[ 1 - \frac{R^{3}}{r^{3}} \bigg( \frac{\mu_{2} = \mu_{1}}{\mu_{2} + 2 \mu_{1}} \bigg) \bigg] \sin \theta \textbf{i}_{\theta} \right \}, & r > R \end{matrix} \right. \nonumber \]

Las líneas del campo magnético se trazan en la Figura 5-25a cuando\(\mu_{2} \rightarrow \infty\). En este límite, H dentro de la esfera es cero, de manera que las líneas de campo que inciden sobre la esfera son puramente radiales. Las líneas de campo trazadas son solo líneas de función de flujo constante\(\Sigma\), encontradas de la misma manera que para el problema análogo del campo eléctrico en la Sección 4-4-3b

. (ii) Si la esfera está perfectamente conductora, el campo magnético interno es cero de manera que A = 0. El componente normal de B justo fuera de la esfera es entonces también cero:

\[H_{r}(r = R_{+}) = 0 \Rightarrow C = H_{0}R^{3}/2 \nonumber \]

dando la solución

\[\textbf{H} = H_{0} \bigg[ \(1 - \frac{R^{3}{r^{3}} \bigg) \cos \theta \textbf{i}_{r} - \bigg( 1 + \frac{R^{3}}{2r^{3}} \bigg) \sin \theta \textbf{i}_{\theta} \bigg], \: \: \: \: r > R \nonumber \]

La corriente superficial interfacial a r = R se obtiene de la discontinuidad en el componente tangencial de H:

\[K_{\phi} = H_{\phi} (r = R) = - \frac{3}{2}H_{0} \sin \theta \nonumber \]

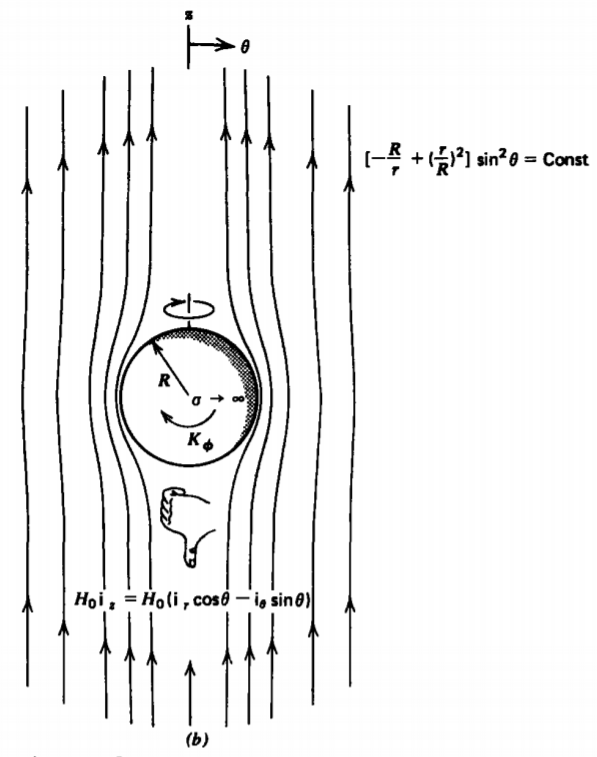
La corriente fluye en\(\phi\) dirección negativa alrededor de la esfera. La regla de la derecha, ilustrada en la Figura 5-25b, muestra que el campo resultante de la corriente inducida actúa en la dirección opuesta al campo impuesto. Esta oposición da como resultado el campo magnético cero dentro de la esfera.

Las líneas de campo trazadas en la Figura 5-25b son puramente tangenciales a la esfera perfectamente conductora como se requiere en (14)

(iii) Si ambas regiones están uniformemente magnetizadas, las condiciones límite son

\[H_{\theta} (r = R_{+}) = H_{\theta} (r = R_{-}) \Rightarrow A = D + C/R^{3} \\ B_{r} (R = R_{+}) = B_{r}(r = R_{-}) \Rightarrow H_{r}(r = R_{+}) + M_{1} \cos \theta \\ H_{r} ( r = R_{-}) + M_{2} \cos \theta \nonumber \]

con soluciones

\[A = H_{0} + \frac{1}{3}(M_{1} - M_{2}) \\ C = \frac{R^{3}}{3} (M_{1} - M_{2}) \nonumber \]

para que el campo magnético sea

\[\textbf{H} = \left \{ \begin{ [H_{0} + \frac{1}{3} (M_{1} - M_{2})][\cos \theta \textbf{i}_{r} - \sin \theta \textbf{i}_{\theta}] \\ \: \: \: [H_{0} + \frac{1}{3} (M_{1} - M_{2})] \textbf{i}_{z} & r < R \\ \bigg( H_{0} - \frac{2R^{3}}{3 r^{3}} (M_{1} - M_{2}) \bigg) \cos \theta \textbf{i}_{r} \\ - \bigg( H_{0} + \frac{R^{3}}{3 r^{3}} (M_{1} - M_{2} ) \bigg) \sin \theta \textbf{i}_{\theta} & r > R \end{matrix} \right. \nonumber \]

Debido a que la magnetización es uniforme en cada región, el rizo de M es cero en todas partes pero en la superficie de la esfera, de manera que la corriente de magnetización de volumen es cero con una corriente de magnetización superficial a r = R dada por

\[\textbf{K}_{m} = \textbf{n} \times (\textbf{M}_{1} - \textbf{M}_{2}) \\ = \textbf{i}_{r} \times (M_{1} - M_{2}) \textbf{i}_{z} \\ = \textbf{i}_{r} \times (M_{1} - M_{2}) (\textbf{i}_{r} \cos \theta - \sin \theta \textbf{i}_{\theta}) = - (M_{1} - M_{2} ) \sin \theta \textbf{i}_{\phi} \nonumber \]