8.7: Guía de ondas dieléctrica

Encontramos en la Sección 7-10-6 para fibra óptica que las ondas electromagnéticas también pueden ser guiadas por estructuras dieléctricas si la onda viaja desde el dieléctrico al espacio libre en un ángulo de incidencia mayor que el ángulo crítico. Las ondas que se propagan a lo largo del dieléctrico de espesor\(2d\) en la Figura 8-30 todavía se describen mediante las ecuaciones de onda vectorial derivadas en la Sección 8-6-1.

Soluciones TM

Deseamos encontrar soluciones donde los campos estén esencialmente confinados dentro del dieléctrico. Descuidamos las variaciones con\(y\) tal que para\(\textrm{TM}\) las ondas que se propagan en la\(z\) dirección el\(z\) componente del campo eléctrico se da en la Sección 8-6-2 como

\ begin {ecuación} E_ {z}\ left (x, t\ right) =\ left\ {\ begin {array} {ll}
\ textrm {Re}\ left [A_ {2} e^ {-\ alpha\ left (x-d\ right)} e^ {j\ left (\ omega t-k_ {z} z\ right)}\ right], &x\ geq d\
\ textrm {Re}\ izquierda [\ izquierda (A_ {1}\ sin k_ {x} x+b_ {1}\ cos k_ {x} x\ derecha) e^ {j\ izquierda (\ omega t-k_ {z} z\ derecha)}\ derecha], &\ izquierda | x\ derecha |\ leq d\
\ textrm {Re}\ izquierda [A_ {3} e^ {\ alfa\ izquierda (x+d\ derecha)} e^ {j\ izquierda (\ omega t-k_ {z} z\ derecha)}\ derecha], &x\ leq -d
\ end {array}\ derecha. \ end {ecuación}

Figura 8-30\(\textrm{TE}\) y\(\textrm{TM}\) modos también pueden propagarse a lo largo de estructuras dieléctricas. Los campos pueden estar esencialmente confinados al dieléctrico en un rango de frecuencia si la velocidad de la onda en el dieléctrico es menor que la del exterior. Es conveniente separar las soluciones en modos par e impar.

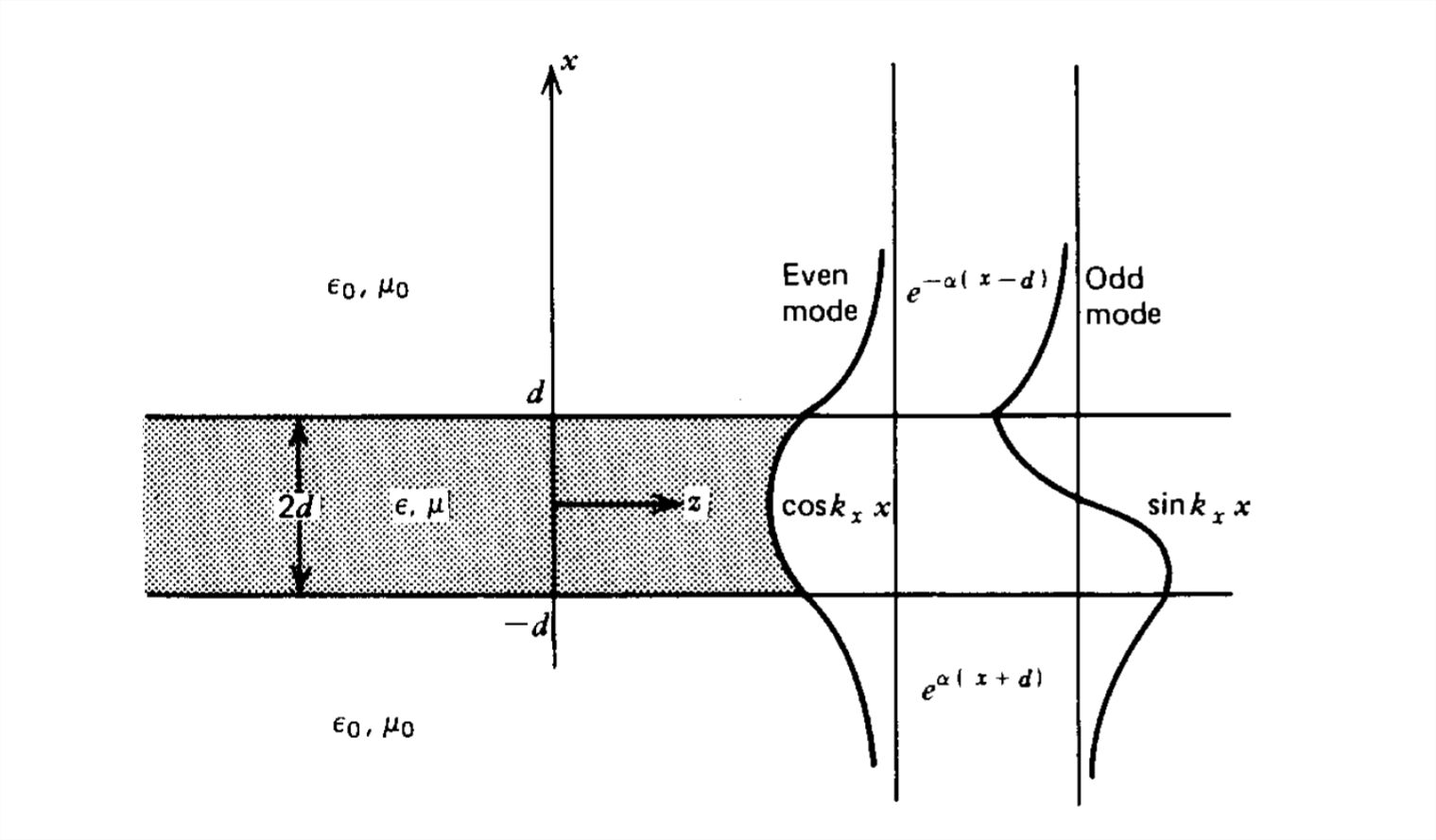
donde elegimos escribir la solución fuera del dieléctrico en forma de onda en descomposición para que los campos se localizan predominantemente alrededor del dieléctrico.

Los números de onda y la tasa de decadencia obedecen a las relaciones

\ [k_ {x} ^ {2} +k_ {z} ^ {2} =\ omega^ {2}\ varepsilon\ mu\
-\ alfa ^ {2} +k_ {z} ^ {2} =\ omega^ {2}\ varepsilon_ {0}\ mu _ {0}\ nonumber\]

El\(z\) componente del número de onda debe ser el mismo en todas las regiones para que se puedan cumplir las condiciones de contorno en cada interfaz. Para la propagación en el dieléctrico y la evanescencia en el espacio libre, debemos tener eso

\[ \omega^{2}\varepsilon_{0}\mu _{0}< k_{z}< \omega^{2}\varepsilon\mu \nonumber \]

Todos los demás componentes del campo eléctrico y magnético se pueden encontrar en (1) de la misma manera que para las guías de onda metálicas en la Sección 8-6-2. Sin embargo, es conveniente considerar por separado cada una de las soluciones para\(E_{z}\) dentro del dieléctrico.

(a) Soluciones impares

Si\(E_{z}\) en cada medio plano por encima y por debajo de la línea central están dirigidos de manera opuesta, el campo dentro del dieléctrico debe variar únicamente como\(k_{x}x\):

\ [\ begin {align}\ hat {E} _ _ {z} =\ left\ {\ begin {array} {ll}
A_ {2} e^ {-\ alpha\ left (x-d\ right)}, &\ quad x\ geq d\\
A_ {1}\ sin k_ {x} x, &\ quad\ izquierda | x\ derecha |\ leq d\\
A_ {} e^ {\ alpha\ left (x+d\ right)}, &\ quad x\ leq -d
\ end {array}\ right. \ end {align}\ nonumber\]

Entonces porque a falta de carga volumétrica el campo eléctrico no tiene divergencia,

\ [\ begin {align}\ frac {\ parcial\ sombrero {E} _ {x}} {\ parcial x} -jk_ {z}\ hat {E} _ {z}\ Rightarrow\ hat {E} _ _ {x} =\ left\ {\ begin {array} {ll}
\ displaystyle -\ frac {jk_ {z}} {\ alpha} A_ {2} e^ {-\ alfa\ izquierda (x-d\ derecha)}, &\ quad x\ geq d\\
\ displaystyle -\ frac {jk_ {z}} {k_ {x}} A_ {1}\ cos k_ {x} x, &\ quad\ izquierda | x\ derecha |\ leq d\\
\ displaystyle\ frac {jk_ {z}} {\ alpha} A_ {3} e^ {\ alpha\ left (x+d\ right)}, &\ quad x\ leq -d
\ end {array}\ right. \ end {align}\ nonumber\]

mientras que de la ley de Faraday el campo magnético es

\ [\ begin {align}\ hat {H} _ {y} =-\ frac {1} {j\ omega\ mu}\ left (-jk_ {z}\ hat {E} _ {x} -\ frac {\ parcial\ hat {E} _ {z}} {\ parcial x}\ derecha)\ nonumber\
\ Rightarrow\ hat {H} _ {y} =\ left\ {\ begin {array} {ll}
\ displaystyle -\ frac {j\ omega\ varepsilon _ {0} A_ {2}} {\ alpha} e^ {-\ alpha\ left (x-d\ right)}, & amp;\ quad x\ geq d\\
\ displaystyle -\ frac {j\ omega\ varepsilon A_ {1}} {k_ {x}}\ cos k_ {x} x, &\ quad\ izquierda | x\ derecha |\ leq d\
\\ displaystyle\ frac {j\ omega\ varepsilon _ {0} A_ {3}} {alfa} e^ {\ alpha\ left (x+d\ right)}, &\ quad x\ leq -d
\ end {array}\ right. \ end {align}\ nonumber\]

En los límites donde\(x=\pm d\) los campos tangenciales eléctricos y magnéticos son continuos:

\ begin {align} E_ {z}\ izquierda (x=\ pm d_ {-}\ derecha) =E_ {z}\ izquierda (x=\ pm d_ {+}\ derecha)\ fila derecha &A_ {1}\ sin k_ {x} d=a_ {2}\ nonumber\\ &
-A_ {1}\ sin k_ {x} d=a_ {3}\ nonumber\\
H_ {y}\ izquierda (x=\ pm d_ {-}\ derecha) =H_ {y}\ izquierda (x=\ pm d_ {+}\ derecha)\ Rightarrow &\ frac {-j\ omega\ varepsilon A_ { 1}} {k_ {x}}\ cos k_ {x} d=\ frac {-j\ omega\ varepsilon_ {0} A_ {2}} {\ alfa}\ nonumber\\ &
\ frac {-j\ omega\ varepsilon A_ {1}} {k_ {x}}\ cos k_ {x} d=\ frac j\ omega\ varepsilon_ {0} A_ {3}} {\ alpha}\ end {align}

que al resolverse simultáneamente rinde

\ [\ izquierda. \ begin {matrix}
\ displaystyle\ frac {A_ {2}} {A_ {1}} =\ sin k_ {x} d=\ frac {\ varepsilon\ alpha} {\ varepsilon _ {0} k_ {x}}\ cos k_ {x} d\\
\ displaystyle\ frac {A_ {3}} {A_ {1}} =-\ sin k_ {x} d=-\ frac {\ varepsilon\ alfa} {\ varepsilon _ {0} k_ {x}}\ cos k_ {x} d
\ final {matriz}\ derecha\}\ Derecha\ alfa =\ frac {\ varepsilon _ {0}} {\ varepsilon} k_ {x}\ tan k_ {x} d\ nonumber\]

Los valores permitidos de\(\alpha\) y\(k_{x}\) se obtienen mediante resolución autoconsistente (8) y (2), lo que en general requiere un método numérico. La condición crítica para una onda guiada ocurre cuando\(\alpha =0\), lo que requiere eso\(k_{x}d=n\pi \) y\(k_{z}^{2}=\omega ^{2}\varepsilon _{0}\mu _{0}\). La frecuencia crítica se obtiene a partir de (2) como

\[ \omega ^{2}=\frac{k_{x}^{2}}{\varepsilon \mu -\varepsilon _{0}\mu _{0} }=\frac{\left ( n\pi /d \right )^{2}}{\varepsilon \mu -\varepsilon _{0}\mu _{0} } \nonumber \]

Tenga en cuenta que esto ocurre para frecuencias reales solo si\(\varepsilon \mu > \varepsilon _{0}\mu _{0} \).

(b) Incluso Soluciones

Si\(E_{z}\) está en la misma dirección por encima y por debajo del dieléctrico, las soluciones son similares

\ begin {align}\ hat {E} _ _ {z} =\ left\ {\ begin {array} {ll}
B_ {2} e^ {-\ alpha\ left (x-d\ right)}, &\ quad x\ geq d\\
B_ {1}\ cos k_ {x} x, &\ quad\ izquierda | x\ derecha |\ leq d\\
B_ {3} e^ {\ alpha\ left (x+d\ right)}, &\ quad x\ leq -d
\ end {array}\ right. \ end {align}

\ begin {align}\ hat {E} _ _ {x} =\ left\ {\ begin {array} {ll}
\ displaystyle -\ frac {jk_ {z}} {\ alpha} B_ {2} e^ {-\ alpha\ left (x-d\ right)}, &\ quad x\ geq d\\\ displaystyle
\ frac {jk_ {z} {k_ {k_} {k_ {x}} B_ {1}\ sin k_ {x} x, &\ quad\ izquierda | x\ derecha |\ leq d\
\\ displaystyle\ frac {jk_ {z}} {\ alfa} B_ {3} e^ {\ alpha\ left (x+d\ right)}, &\ quad x\ leq -d
\ end {array}\ right. \ end {align}

\ begin {align}\ hat {H} _ {y} =\ left\ {\ begin {array} {ll}
\ displaystyle -\ frac {j\ omega\ varepsilon _ {0}} {\ alpha} B_ {2} e^ {-\ alpha\ left (x-d\ right)}, &\ quad x\ geq d\\
\ displaystyle\ frac {j\ omega\ varepsilon} {k_ {x}} B_ {1}\ sin k_ {x} x, &\ quad\ izquierda | x\ derecha |\ leq d\\
\ displaystyle\ frac {j\ omega\ varepsilon _ {0}} {\ alpha} B_ {3} e^ {\ alpha\ left (x+d\ right)}, &\ quad x\ leq -d
\ end {array}\ right. \ end {align}

Continuidad de los campos tangenciales eléctricos y magnéticos en las\(x=\pm d\) necesidades

\ [B_ {1}\ cos k_ {x} d=b_ {2},\ quad B_ {1}\ cos k_ {x} d=b_ {3}\
\ frac {j\ omega\ varepsilon} {k_ {x}} B_ {1}\ sin k_ {x} d=-\ frac {j\ omega\ varepsilon _ {0}} {\ alfa} B_ {2},\ quad
-\ frac {j\ omega\ varepsilon B_ {1}} {k_ {x}}\ sin k_ {x} d=\ frac {j\ omega\ varepsilon _ {0} B_ {3}} {\ alfa}\ nonumber\]

o

\ [\ izquierda. \ begin {matrix}
\ displaystyle\ frac {B_ {2}} {B_ {1}} =\ cos k_ {x} d=-\ frac {\ varepsilon\ alpha} {\ varepsilon _ {0} k_ {x}}\ sin k_ {x} d\\
\ displaystyle\ frac {B_ {3}} {B_ {1}} =\ cos k_ {x} d=-\ frac {\ varepsilon\ alfa} {\ varepsilon _ {0} k_ {x}}\ sin k_ {x} d
\ final {matriz}\ derecha\}\ Derecha\ alfa =-\ frac {\ varepsilon _ {0} k_ {x}} {\ varepsilon}\ cuna k_ {x} d\ nonumber\]

Soluciones TE

El mismo procedimiento se realiza para las\(\textrm{TE}\) soluciones resolviendo primero para\(H_{z}\).

(a) Soluciones impares

\ begin {align}\ hat {H} _ _ {z} =\ left\ {\ begin {array} {ll}
A_ {2} e^ {-\ alpha\ left (x-d\ right)}, &\ quad x\ geq d\\
A_ {1}\ sin k_ {x} x, &\ quad\ izquierda | x\ derecha |\ leq d\\
A_ {3} e_ ^ {\ alpha\ left (x+d\ right)}, &\ quad x\ leq -d
\ end {array}\ right. \ end {align}

\ begin {align}\ hat {H} _ _ {x} =\ left\ {\ begin {array} {ll}
\ displaystyle -\ frac {jk_ {z}} {\ alpha} A_ {2} e^ {-\ alpha\ left (x-d\ right)}, &\ quad x\ geq d\\\ displaystyle -
\ frac {jk_ {z}} {k{ k_} {k_ {x}} A_ {1}\ cos k_ {x} x, &\ quad\ izquierda | x\ derecha |\ leq d\
\\ displaystyle\ frac {jk_ {z}} {\ alfa} A_ {3} e^ {\ alpha\ left (x+d\ right)}, &\ quad x\ leq -d
\ end {array}\ right. \ end {align}

\ begin {align}
\ hat {E} _ {y} =\ left\ {\ begin {array} {ll}
\ displaystyle\ frac {j\ omega\ mu _ {0}} {\ alpha} A_ {2} e^ {-\ alpha\ left (x-d\ right)}, &\ quad x\ geq d\\
\ displaystyle\ frac {j\ omega\ mu} k{ _ {x}} A_ {1}\ cos k_ {x} x, &\ quad\ izquierda | x\ derecha |\ leq d\\
\ displaystyle -\ frac {j\ omega\ mu _ {0}} {\ alpha} A_ {3} e^ {\ alpha\ left (x+d\ right)}, &\ quad x\ leq -d
\ end {array}\ right. \ end {align}

donde la continuidad de tangencial\(\textbf{E}\) y\(\textbf{H}\) a través de los límites requiere

\[\alpha =\frac{\mu _{0}}{\mu }k_{x}\tan k_{x}d \nonumber \]

(b) Incluso Soluciones

\ begin {align}\ hat {H} _ _ {z} =\ left\ {\ begin {array} {ll}
B_ {2} e^ {-\ alpha\ left (x-d\ right)}, &\ quad x\ geq d\\
B_ {1}\ cos k_ {x} x, &\ quad\ izquierda | x\ derecha |\ leq d\\
B_ {3} e^ {\ alpha\ left (x+d\ right)}, &\ quad x\ leq -d
\ end {array}\ right. \ end {align}

\ begin {align}\ hat {H} _ _ {x} =\ left\ {\ begin {array} {ll}
\ displaystyle -\ frac {jk_ {z}} {\ alpha} B_ {2} e^ {-\ alpha\ left (x-d\ right)}, &\ quad x\ geq d\\\ displaystyle
\ frac {jk_ {z} {k_ {k_} {k_ {x}} B_ {1}\ sin k_ {x} x, &\ quad\ izquierda | x\ derecha |\ leq d\
\\ displaystyle\ frac {jk_ {z}} {\ alfa} B_ {3} e^ {\ alpha\ left (x+d\ right)}, &\ quad x\ leq -d
\ end {array}\ right. \ end {align}

\ begin {align}\ hat {E} _ {y} =\ left\ {\ begin {array} {ll}
\ displaystyle\ frac {j\ omega\ mu _ {0}} {\ alpha} B_ {2} e^ {-\ alpha\ left (x-d\ right)}, &\ quad x\ geq d\
\\ displaystyle -\ frac {j\ omega\ mu} k_ {x}} B_ {1}\ sin k_ {x} x, &\ quad\ izquierda | x\ derecha |\ leq d\\
\ displaystyle - \ frac {j\ omega\ mu_ {0}} {\ alpha} B_ {3} e^ {\ alpha\ left (x+d\ right)}, &\ quad x\ leq -d
\ end {array}\ right. \ end {align}

donde\(\alpha\) y\(k_{x}\) están relacionados como

\[ \alpha =-\frac{\mu _{0}}{\mu }k_{x}\cot k_{x}d \nonumber \]