2.5: La FFT como Evaluación Recursiva de la DFT

Última actualización
Guardar como PDF

Page ID: 86965

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Es posible formular la DFT de manera que una longitud-\(N\) DFT se pueda calcular en términos de dos DFT de longitud- (\(N/2\)).

Y, si\(N=2^{M}\) cada una de esas DFT de longitud- (\(N/2\)) se puede encontrar en términos de longitud- (\(N/4\)) DFT. Esto permite calcular la DFT mediante un algoritmo recursivo con\(M\) recursiones, dando al orden familiar la complejidad\(N\log N\) aritmética.

Calcule los valores de DFT indexados pares a partir de la ecuación por:

\[C(2k)=\sum_{n=0}^{N-1}x(n)W_{N}^{2nk}=\sum_{n=0}^{N-1}x(n)W_{N/2}^{nk} \nonumber \]

\[C(2k)=\sum_{n=0}^{N/2-1}x(n)W_{N}^{2nk}+\sum_{n=N/2}^{N-1}x(n)W_{N/2}^{nk} \nonumber \]

\[C(2k)=\sum_{n=0}^{N/2-1}\left \{ x(n)+x(n+N/2)\right \}W_{N/2}^{nk} \nonumber \]

y un argumento similar da los valores indexados impares como:

\[C(2k+1)=\sum_{n=0}^{N/2-1}\left \{ x(n)-x(n+N/2)\right \}W_{N}^{n}W_{N/2}^{nk} \nonumber \]

En conjunto, estas son fórmulas de DFT recursivas que expresan la DFT de longitud-N\(x(n)\) en términos de DFT de longitud-N/2:

\[C(2k)=DFT_{N/2}\left \{ x(n)+x(n+N/2)\right \} \nonumber \]

\[C(2k+1)=DFT_{N/2}\left \{ [x(n)-x(n+N/2)]W_{N}^{n}\right \} \nonumber \]

Esta es una versión de “decimation-in-frequency” (DIF) ya que da muestras de la representación en el dominio de la frecuencia en términos de bloques de la señal en el dominio del tiempo.

Un programa recursivo de Matlab que implementa esto viene dado por:

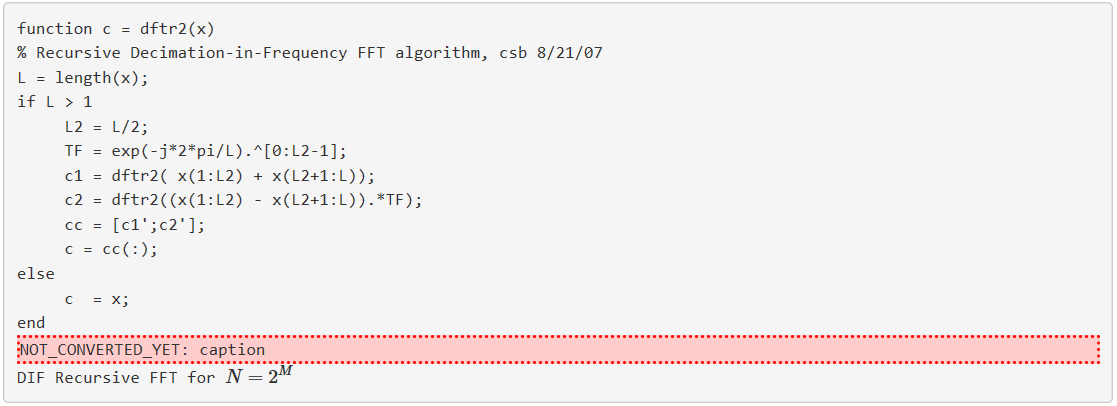
Una versión DIT se puede derivar en la forma:

\[C(k)=DFT_{N/2}\left \{ x(2n)\right \}+W_{N}^{k}DFT_{N/2}\left \{ x(2n+1)\right \} \nonumber \]

\[C(k+N/2)=DFT_{N/2}\left \{ x(2n)\right \}-W_{N}^{k}DFT_{N/2}\left \{ x(2n+1)\right \} \nonumber \]

que da bloques del dominio de frecuencia a partir de muestras de la señal.

Un programa recursivo de Matlab que implementa esto viene dado por:

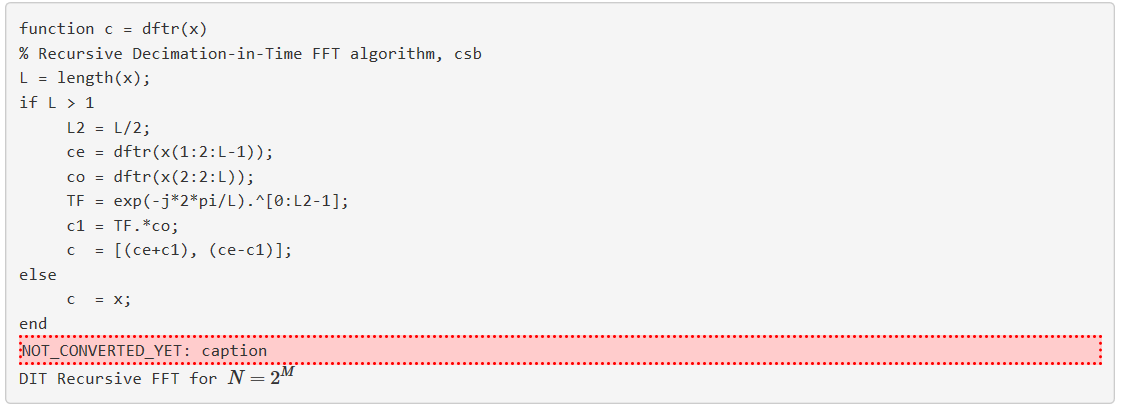
Se pueden desarrollar expresiones recursivas similares para otras radices y algoritmos. La mayoría de los programas recursivos no se ejecutan tan eficientemente como el código en bucle o recto, pero algunos pueden ser muy eficientes, por ejemplo, partes del FFTW.

Tenga en cuenta que una\(2^M\) secuencia de longitud requerirá\(M\) recursiones, cada una de las cuales requerirá\(N/2\) multiplicaciones. Esto da la\(N\log N\) fórmula que los otros enfoques también derivan.

Colaborador

ContribeeBurrus