6.2: Algoritmo de transformada de Fourier de Winograd (WFTA)
- Page ID
- 86875
La operación de convolución discreta definida por
\[y(n)=\sum_{k}h(n-k)x(k) \nonumber \]
se llama operación bilineal porque, para un fijo\(h(n)\),\(y(n)\) es una función lineal de\(x(n)\) y para un fijo\(x(n)\) es una función lineal de\(h(n)\). El funcionamiento de convolución cíclica es el mismo pero con todos los índices evaluados módulo\(N\).
Recordar de polinomio Descripción de señales que longitud- convolución\(N\) cíclica de\(x(n)\) y\(h(n)\) puede ser representada por multiplicación polinómica
\[Y(s)=X(s)H(s)\; mod\; (s^{N}-1) \nonumber \]
Esta operación bilineal también se puede expresar en términos de operadores de matriz lineal y un operador bilineal más simple denotado por el\(o\) cual puede ser solo una simple multiplicación elemento por elemento de los dos vectores. Esta formulación matricial es
\[Y=C\left [ AX_{0}BH \right ] \nonumber \]
donde\(X\),\(H\) y\(Y\) son\(N\) vectores de longitud con elementos de\(x(n)\)\(h(n)\), y\(y(n)\) respectivamente. Las matrices\(A\) y\(B\) tienen dimensión\(M\times N\), y\(C\) es\ [N\ veces M\) con\(M\geq N\).
Los elementos de\(A\),\(B\), y\(C\) están restringidos a ser simples; típicamente números enteros pequeños o números racionales. Serán estos operadores matriciales los que hagan el equivalente de la reducción de residuos en los polinomios en la ecuación.
Para derivar un algoritmo útil, considere nuevamente la ecuación de formulación polinómica. Para utilizar el esquema de reducción de residuos, el módulo se factoriza en factores relativamente primos. Afortunadamente el factorización de este polinomio en particular,\(s^N-1\), ha sido ampliamente estudiado y tiene una estructura considerable. Cuando se factorizan sobre los racionales, lo que significa que los únicos coeficientes permitidos son los números racionales, los factores se denominan polinomios ciclotómicos. La propiedad más interesante para nuestros fines es que la mayoría de los coeficientes de los polinomios ciclotómicos son cero y los demás son más o menos unidad para grados de hasta más de cien. Esto significa que la reducción de residuos generalmente no requerirá multiplicaciones.
Las operaciones de reducción\(X(s)\) y\(H(s)\) en la ecuación son llevadas a cabo por las matrices\(A\) y\(B\) en la ecuación. La convolución de los polinomios de residuos es realizada por el\(o\) operador y la recombinación por el CRT se realiza por la\(C\) matriz. El hecho importante es que las\(B\) matrices\(A\) y generalmente contienen solo entradas de unidad cero y más o menos y la\(C\) matriz solo contiene números racionales. Las únicas multiplicaciones generales son las representadas por\(o\). En efecto, en los resultados teóricos de la teoría de la complejidad computacional, estas multiplicaciones reales o complejas suelen ser las únicas contadas. En algoritmos prácticos, las multiplicaciones racionales representadas por\(C\) podrían ser un factor limitante.
Los\(h(n)\) términos son fijos para un filtro digital, o representan los\(W\) términos del Mapeo de Índice Multidimensional si la convolución se está utilizando para calcular una DFT. Debido a esto,\(d=BH\) en la ecuación se puede precalcular y solo los\(C\) operadores\(A\) y representan las matemáticas realizadas en la ejecución del algoritmo. Para explotar esta característica, se demostró que las propiedades de la ecuación permiten el intercambio del operador más complicado\(C\) con el operador más simple\(B\). Específicamente esto viene dado por
\[Y=C\left [ AX_{0}BH \right ] \nonumber \]
\[Y'=B^{T}\left [ AX_{0}C^{T}H' \right ] \nonumber \]
donde\(H'\) tiene los mismos elementos que\(H\), pero en un orden permutado, e igualmente\(Y'\) y\(Y\). Esta propiedad muy importante permite precalcular lo más complicado\(C^TH'\) en la ecuación en lugar de\(BH\) como en la ecuación anterior.
Debido a que\(BH\) o\(C^TH'\) puede precalcularse, la forma bilineal de las ecuaciones anteriores puede escribirse como una forma lineal. Si una matriz\(M\times M\) diagonal\(D\) se forma a partir de\(d=C^TH'\), o en el caso de la ecuación,\(d=BH\), asumiendo una propiedad conmutativa para\(o\), las ecuaciones se convierten
\[Y'=B^{T}DAX \nonumber \]
\[Y=CDAX \nonumber \]
En la mayoría de los casos no hay razón para no usar las mismas operaciones de reducción en\(X\) y\(H\), por lo tanto,\(B\) puede ser lo mismo que\(A\) y la ecuación entonces se convierte
\[Y'=A^{T}DAX \nonumber \]
Para ilustrar cómo se lleva a cabo la reducción de residuos y cómo se obtiene la\(A\) matriz, se continuará el algoritmo length-\(5\) DFT iniciado en La DFT como Convolución o Filtrado. El DFT se convierte primero en una convolución\(4\) cíclica de longitud por la permutación del índice de La DFT como Convolución o Filtrado para dar la convolución cíclica en La DFT como Convolución o Filtrado. Para evitar confusiones del orden permutado de los datos\(x(n)\) en El DFT como Convolución o Filtrado, primero se desarrollará la convolución cíclica sin la permutación, utilizando el polinomio\(U(s)\)
\[U(s)=x(1)+x(3)s+x(4)s^{2}+x(2)s^{3} \nonumber \]
\[U(s)=u(0)+u(1)s+u(2)s^{2}+u(3)s^{3} \nonumber \]
y luego los resultados se convertirán de nuevo a los permutados\(x(n)\). La convolución\(4\) cíclica de longitud en términos de polinomios es
\[Y(s)=U(s)H(s)\; mod\; (s^{4}-1) \nonumber \]
y los factores de módulo en tres polinomios ciclotómicos
\[s^{4}-1=(s^{2}-1)(s^{2}+1) \nonumber \]
\[s^{4}-1=(s-1)(s+1)(s^{2}+1) \nonumber \]
\[s^{4}-1=P_{1}P_{2}P_{3} \nonumber \]
Ambos\(U(s)\) y\(H(s)\) se reducen el módulo de estos tres polinomios. El módulo de reducción\(P_1\) y\(P_2\) se realiza en dos etapas. Primero se hace módulo (\(s^2-1\)), luego ese residuo se reduce aún más módulo (\(s-1\)) y (\(s+1\).
\[U(s)=u_{0}+u_{1}s+u_{2}s^{2}+u_{3}s^{3} \nonumber \]
\[U'(s)=((U(s)))_{(s^{2}-1)}=(u_{0}+u_{2})+(u_{1}+u_{3})s \nonumber \]
\[U1(s)=((U'(s)))_{P_{1}}=(u_{0}+u_{1}+u_{2}+u_{3}) \nonumber \]
\[U2(s)=((U'(s)))_{P_{2}}=(u_{0}-u_{1}+u_{2}-u_{3}) \nonumber \]
\[U3(s)=((U'(s)))_{P_{3}}=(u_{0}-u_{2})+(u_{1}-u_{3})s \nonumber \]
La reducción en la ecuación de la ecuación polinómica de datos puede ser denotada por una operación matricial en un vector que tiene los datos como entradas.
\[\begin{bmatrix} 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 1 \end{bmatrix}\begin{bmatrix} u_{0}\\ u_{1}\\ u_{2}\\ u_{3} \end{bmatrix}=\begin{bmatrix} u_{0}+u_{2} \\ u_{1}+u_{3} \end{bmatrix} \nonumber \]
y la reducción en la ecuación es
\[\begin{bmatrix} 1 & 0 & -1 & 0\\ 0 & 1 & 0 & -1 \end{bmatrix}\begin{bmatrix} u_{0}\\ u_{1}\\ u_{2}\\ u_{3} \end{bmatrix}=\begin{bmatrix} u_{0}-u_{2} \\ u_{1}-u_{3} \end{bmatrix} \nonumber \]
La combinación de las dos ecuaciones da un operador
\[\begin{bmatrix} 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 1\\ 1 & 0 & -1 & 0\\ 0 & 1 & 0 & -1 \end{bmatrix}\begin{bmatrix} u_{0}+u_{2}\\ u_{1}+u_{3}\\ u_{0}-u_{2}\\ u_{1}-u_{3} \end{bmatrix}=\begin{bmatrix} u_{0}+u_{2}\\ u_{1}+u_{3}\\ u_{0}-u_{2} \\ u_{1}-u_{3} \end{bmatrix}=\begin{bmatrix} w_{0}\\ w_{1}\\ v_{0}\\ v_{1} \end{bmatrix} \nonumber \]
Una mayor reducción de no\(v_{0}+v_{1}s\) es posible porque\(P_{3}=s^{2}+1\) no se puede factorizar sobre los racionales. Sin embargo, se\(s^{2}-1\) puede tener en cuenta\(P_{1}P_{2}=(s-1)(s+1)\) y, por lo tanto, se\(w_{0}+w_{1}s\) puede reducir aún más como se hizo en las ecuaciones anteriores por
\[\begin{bmatrix} 1 & 1 \end{bmatrix}\begin{bmatrix} w_{0}\\ w_{1} \end{bmatrix}=w_{0}+w_{1}=u_{0}+u_{2}+u_{1}+u_{3} \nonumber \]
Combinando todas las ecuaciones da
\[\begin{bmatrix} 1 & 1 & 0 & 0\\ 1 & -1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 1\\ 1 & 0 & -1 & 0\\ 0 & 1 & 0 & -1 \end{bmatrix}\begin{bmatrix} u_{0}\\ u_{1}\\ u_{2}\\ u_{3} \end{bmatrix}=\begin{bmatrix} r_{0}\\ r_{1}\\ v_{0}\\ v_{1} \end{bmatrix} \nonumber \]
La misma reducción se realiza\(H(s)\) y luego la convolución de la ecuación se realiza multiplicando cada polinomio de residuo de\(X(s)\) y\(H(s)\) módulo de cada factor ciclotómico correspondiente de\(P(s)\) y finalmente una recombinación usando el polinomio chino del teorema del resto (TRC) como en Descripción Polinomial de Señales.
\[Y(s)=K_{1}(s)U_{1}(s)H_{1}(s)+K_{2}(s)U_{2}(s)H_{2}(s)+K_{3}(s)U_{3}(s)H_{3}(s)\; mod\; (s^{4}-1) \nonumber \]
donde\(U_1(s)=r_1\) y\(U_1(s)=r_1\) son constantes y\(U_{3}(s)=v_{0}+v_{1}(s)\) es un polinomio de primer grado. \(U_1\)tiempos\(H_1\) y\(U_2\) tiempos\(H_2\) son fáciles, pero multiplicar\(U_3\) tiempos\(H_3\) modulo (\(s^2+1\)) es más difícil.
La multiplicación de tiempos\(U_3(s)\) tiempos se\(H_3(s)\) puede hacer mediante el algoritmo Toom-Cook que puede ser visto como interpolación Lagrange o multiplicación polinómica módulo un polinomio especial con tres coeficientes arbitrarios. Para simplificar la aritmética, las constantes se eligen para que sean más y menos uno y cero.
Para este ejemplo se puede verificar que
\[((v0+v1s)(h0+h1s))_{s^{2}+1}=(v_{0}h_{0}-v_{1}h_{1})+(v_{0}h_{1}-v_{1}h_{0})s \nonumber \]
que por el algoritmo o inspección de Toom-Cook es
\[\begin{bmatrix} 1 & -1 & 0\\ -1 & -1 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0\\ 0 & 1\\ 1 & 1 \end{bmatrix}\begin{bmatrix} v_{0}\\ v_{1} \end{bmatrix}o\begin{bmatrix} 1 & 0\\ 0 & 1\\ 1 & 1 \end{bmatrix}\begin{bmatrix} h_{0}\\ h_{1} \end{bmatrix}=\begin{bmatrix} y_{0}\\ y_{1} \end{bmatrix} \nonumber \]
donde\(o\) significa multiplicación punto por punto. La\(A\) matriz total en es una combinación de
\[AX=A_{1}A_{2}A_{3}X \nonumber \]
\[AX=\begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 1 \end{bmatrix}\begin{bmatrix} 1 & 1 & 0 & 0\\ 1 & -1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 1\\ 1 & 0 & -1 & 0\\ 0 & 1 & 0 & -1 \end{bmatrix}\begin{bmatrix} u_{0}\\ u_{1}\\ u_{2}\\ u_{3} \end{bmatrix}=\begin{bmatrix} r_{0}\\ r_{1}\\ v_{0}\\ v_{1} \end{bmatrix} \nonumber \]
donde la matriz\(A_3\) da la reducción de residuos (\(s^2-1\)) y (\(s^2+1\)), la parte superior izquierda de\(A_2\) da el módulo de reducción\(s-1\) y\(s+1\), y la parte inferior derecha de\(A_1\) lleva a cabo el algoritmo Toom-Cook módulo\(s^2+1\) con el multiplicación en la\(Y\) ecuación. Observe que al calcular la ecuación en las tres etapas, se requieren siete adiciones. También fíjese que no\(A_1\) es cuadrado. Es esta “expansión” la que provoca que se requieran más que\(N\) multiplicaciones en\(o\) o\(D\) en la\(Y\) ecuación. Esta reducción por etapas derivará al\(A\) operador.
El método descrito anteriormente es muy sencillo para las longitudes de DFT más cortas. Porque\(Y\), ambos polinomios de residuo son constantes y la multiplicación dada por\(o\) en la ecuación es trivial. Porque\(N=5\), que es el ejemplo usado aquí, se requiere una multiplicación polinómica de primer grado pero el algoritmo Toom-Cook utiliza constantes simples y, por lo tanto, funciona bien como se indica en la ecuación. Para\(N=7\), hay dos polinomios de residuos de primer grado que pueden multiplicarse cada uno por las mismas técnicas utilizadas en el\(N=5\) ejemplo. Desafortunadamente, para cualquier longitud más larga, los polinomios de residuos tienen un orden de tres o más, lo que hace que el algoritmo Toom-Cook requiera constantes de más y menos dos y peores. Por esa razón, no se utiliza el método Toom-Cook, y se utilizan otras técnicas como el mapeo de índices que requieren más del número mínimo de multiplicaciones, pero no requieren un número excesivo de adiciones. Los algoritmos resultantes aún tienen la estructura de la ecuación. Blaut y Nussbaumer tienen una buena colección de algoritmos para la multiplicación polinómica que se pueden utilizar con las técnicas aquí discutidas para construir una amplia variedad de algoritmos DFT.
Las constantes en la matriz diagonal se\(D\) pueden encontrar a partir de la matriz CRT\(C\) en la ecuación usando\(d=C^{T}H'\) para los términos diagonales en\(D\). Como se mencionó anteriormente, para las longitudes principales más pequeñas de\(3\),\(5\), y\(7\) esto funciona bien pero para longitudes más largas el CRT se vuelve muy complicado. Un método alternativo para encontrar\(D\) utiliza el hecho de que dado que la forma lineal de las ecuaciones calcula la DFT, es posible calcular una DFT conocida de un dado a\(x(n)\) partir de la definición de la DFT en Mapeo de Índice Multidimensional y, dada la\(A\) matriz en la ecuación, resolver para \(D\)resolviendo un conjunto de ecuaciones simultáneas.
Una modificación de este enfoque también funciona para una longitud que es un primo impar elevado a algún poder:\(N=P^M\). Esto es un poco más complicado pero se ha hecho por longitudes de\(9\), y\(25\). Para longitudes más largas, el algoritmo convencional Cooley-Tukey type- two index map parece ser más eficiente. Para los poderes de dos, no hay raíz primitiva, y por lo tanto, no hay conversión simple de la DFT en convolución. Es posible utilizar dos generadores para realizar la conversión y existe un conjunto de algoritmos de longitud\(4\),\(8\), y\(16\) DFT de la forma en la ecuación.
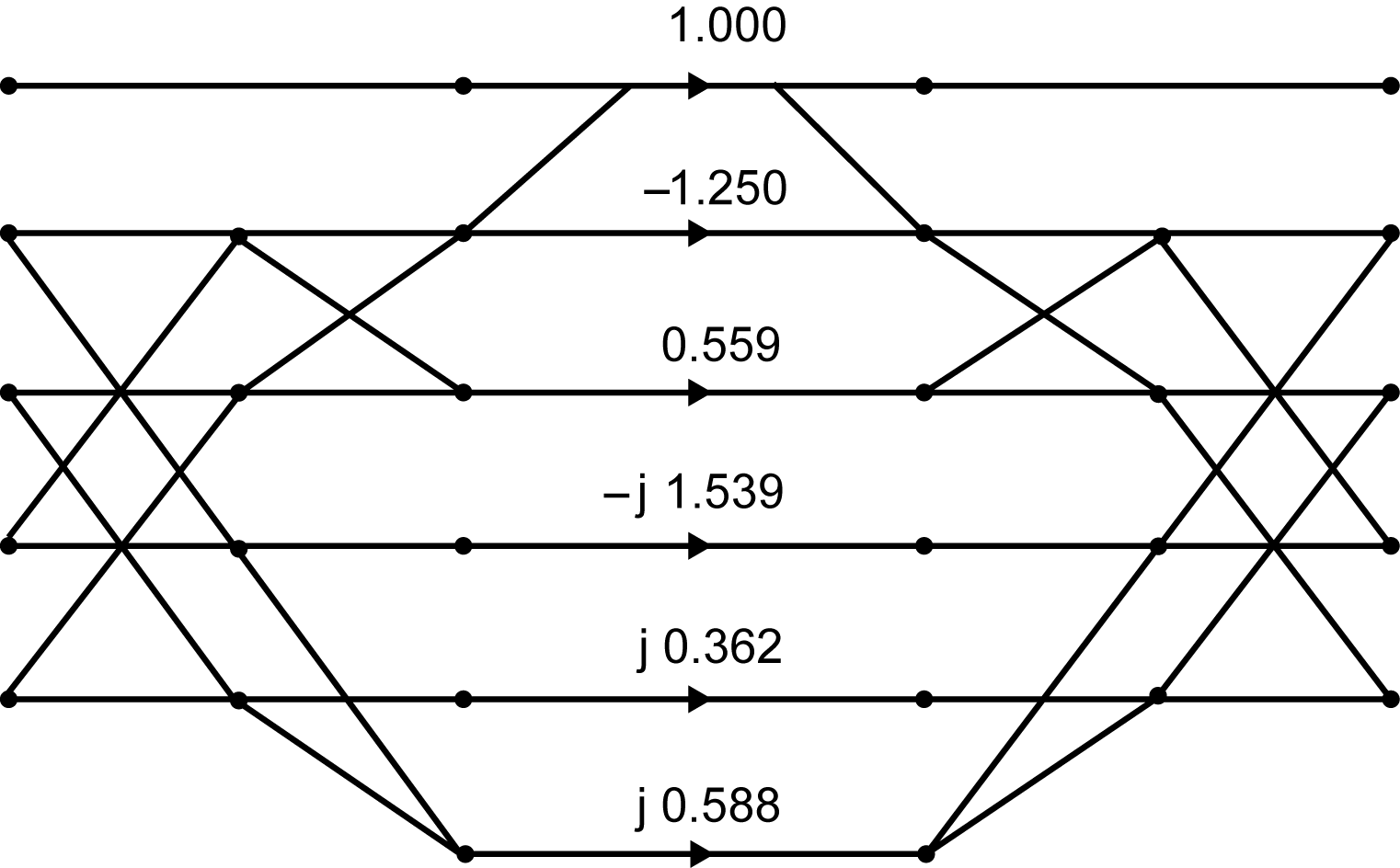
En la Tabla 6.2.1 a continuación se presenta un recuento de operaciones de varios algoritmos de DFT cortos. Estos son algoritmos prácticos que se pueden usar solos o en conjunto con el mapeo de índices para dar DFT más largos como se muestra en Los algoritmos de transformada de Fourier de Factor Primo y Winograd. La mayoría se optimizan al tener ya sea el número mínimo teórico de multiplicaciones o el número mínimo de multiplicaciones sin requerir un número muy grande de adiciones. Algunos permiten otras compensaciones razonables entre números de multiplicaciones y adiciones. Hay dos listas del número de multiplicaciones. El primero es el número de multiplicaciones reales de punto flotante que se deben hacer para esa longitud DFT. Algunas de estas (una o dos en la mayoría de los casos) serán por constantes racionales y las otras serán por constantes irracionales. La segunda lista es el número total de multiplicaciones dadas en la matriz diagonal\(D\) en la ecuación. Al menos uno de estos será unidad (la asociada a\(X(0)\)) y en algunos casos varios serán unidad (para\(N=2^M\)). La segunda lista es importante en la programación del WFTA en The Prime Factor y Winograd Fourier Transform Algorithms.
| Largo N | Mut No-Uno | Total de Mort | Agrega |
| 2 | 0 | 4 | 4 |
| 3 | 4 | 6 | 12 |
| 4 | 0 | 8 | 16 |
| 5 | 10 | 12 | 34 |
| 7 | 16 | 18 | 72 |
| 8 | 4 | 16 | 52 |
| 9 | 20 | 22 | 84 |
| 11 | 40 | 42 | 168 |
| 13 | 40 | 42 | 188 |
| 16 | 20 | 36 | 148 |
| 17 | 70 | 72 | 314 |
| 19 | 76 | 78 | 372 |
| 25 | 132 | 134 | 420 |
| 32 | 68 | - | 388 |
Tabla 6.2.1 Número de multiplicaciones reales y adiciones para una DFT de longitud N de datos complejos
Debido a la estructura de las DFT cortas, el número de multiplicaciones reales requeridas para la DFT de datos reales es exactamente la mitad del requerido para datos complejos. El número de adiciones reales requeridas es ligeramente inferior a la mitad del requerido para datos complejos porque (\(N-1\)) de las adiciones necesarias cuando\(N\) es prime agregan un real a un imaginario, y eso no se realiza realmente. Cuando\(N=2m\), hay (\(N-2\)) de estas pseudo adiciones.
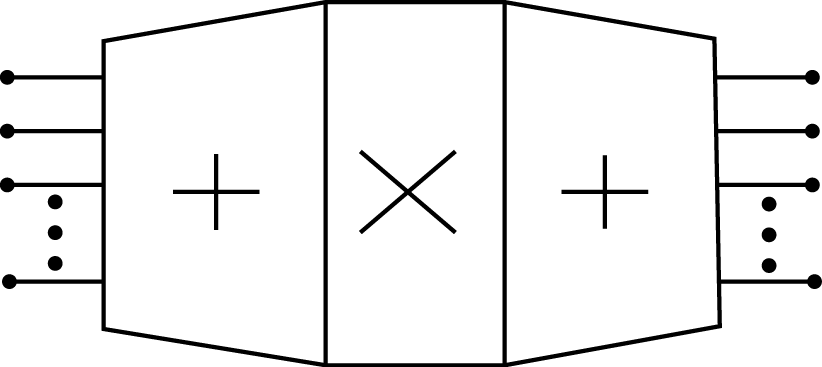
La estructura de estos algoritmos está en la forma de