9.2: El algoritmo del factor primo

Si la DFT se calcula directamente usando la ecuación en 9.1: Introducción, el algoritmo se denomina algoritmo de factor primo y se discutió en Algoritmos DFT cortos de Winograd. Cuando los DFT cortos son calculados por los algoritmos muy eficientes de Winograd discutidos en Factoring the Signal Processing Operators, el PFA se convierte en un método muy potente que es tan rápido o más rápido que los mejores FFT's de Cooley-Tukey.

Un gráfico de flujo no es tan útil con el PFA como lo fue con el FFT de Cooley-Tukey, sin embargo, la siguiente representación en la Fig. 9.2.1 a continuación, que combina las cifras en El Mapa del Índice y el Algoritmo de Transformación de Fourier de Winograd (WFTA) da una buena imagen del algoritmo con el ejemplo de Índice Multidimensional Mapeo.

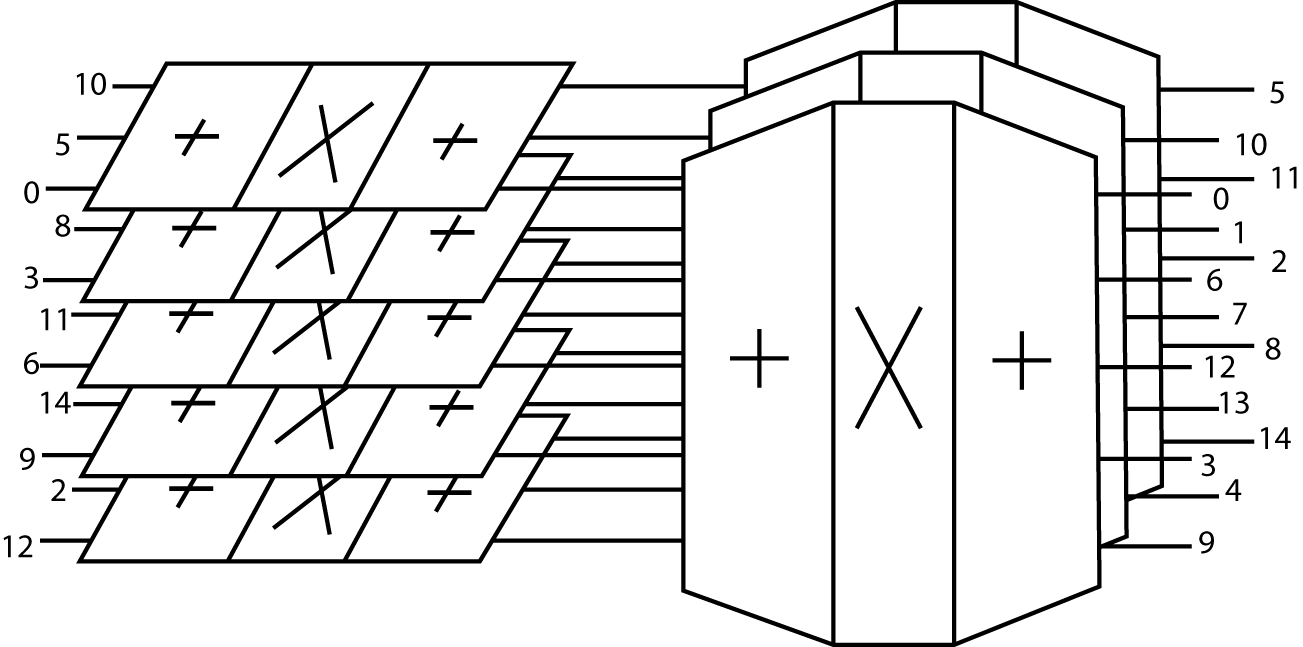
Fig. 9.2.1 Una FFT de factor primo para N = 15

Si\(N\) se factoriza en tres factores, la DFT de la ecuación tendría tres sumaciones anidadas y sería una DFT tridimensional. Este principio se extiende a cualquier número de factores; sin embargo, recordemos que el mapa de Tipo 1 requiere que todos los factores sean relativamente primos. Se ha desarrollado un esquema de indexación de tres bucles muy simple que da un programa PFA compacto y eficiente para cualquier número de factores. La estructura básica del programa se ilustra a continuación con los DFT cortos omitidos para mayor claridad. Los programas completos se dan en los apéndices.

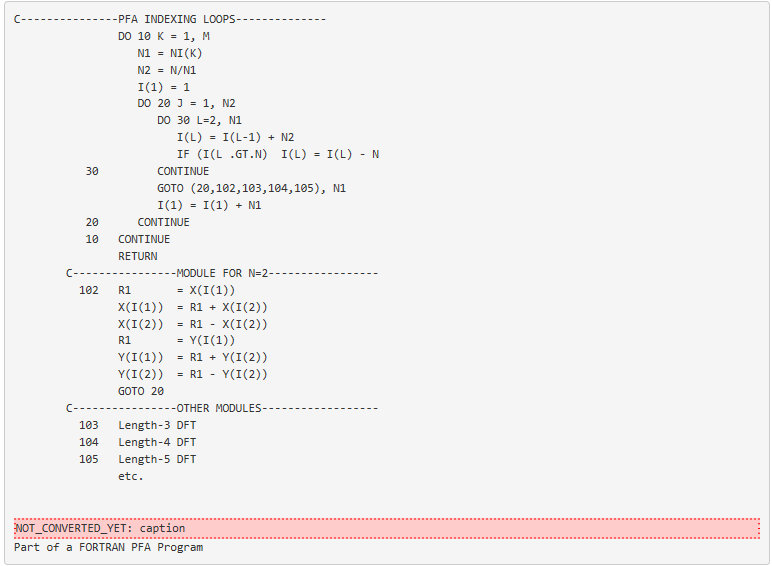
Al igual que en el programa Cooley-Tukey, el bucle DO 10 pasa por las etapas M (factores de N) y el bucle DO 20 calcula las DFT N/N1 Longth-N1. El mapa de índice de entrada de la ecuación se implementa en el bucle DO 30 y la sentencia justo antes de la etiqueta 20. En el PFA, cada etapa o factor requiere un módulo programado por separado o mariposa. Esto alarga el programa PFA pero un programa eficiente de Cooley-Tukey también requerirá tres o más mariposas.

Debido a que el PFA se calcula en el lugar usando el mapa de índice de entrada, la salida se mezcla. Hay cinco enfoques para tratar con esta salida cifrada. Primero, hay algunas aplicaciones donde la salida no tiene que ser descifrada como en el caso de la convolución de alta velocidad. En segundo lugar, se puede agregar un unscrambler después del PFA para dar la salida en el orden correcto así como el contador de bits invertidos se usa para la FFT de Cooley-Tukey. El tercer método realiza el desciframiento en los módulos mientras se están calculando. Este es probablemente el método más rápido pero el programa debe escribirse para una longitud específica. Un cuarto método es similar y logra el desciframiento eligiendo las constantes multiplicadoras en los módulos correctamente. El quinto método utiliza un método de indexación separado para la entrada y salida de cada módulo.

Colaborador

• ContribeeBurrus