14.2: Apéndice 2 - Recuentos de Operación para FFT de Longitud General

La FFT Glassman-Ferguson es una implementación compacta de una FFT Cooley-Tukey de base mixta con los DFT cortos para cada factor calculados por un algoritmo similar a Goertzel. Esto significa que hay multiplicaciones de factores de twiddle incluso cuando los factores son relativamente primos, sin embargo, la indexación es simple y compacta. Calculará la DFT de una secuencia de cualquier longitud pero solo es eficiente si la longitud es altamente compuesta. Las cifras contienen gráficas del número de multiplicaciones de punto flotante más adiciones vs. la longitud de la FFT. Los números en el eje vertical tienen un significado relativo pero no un significado absoluto.

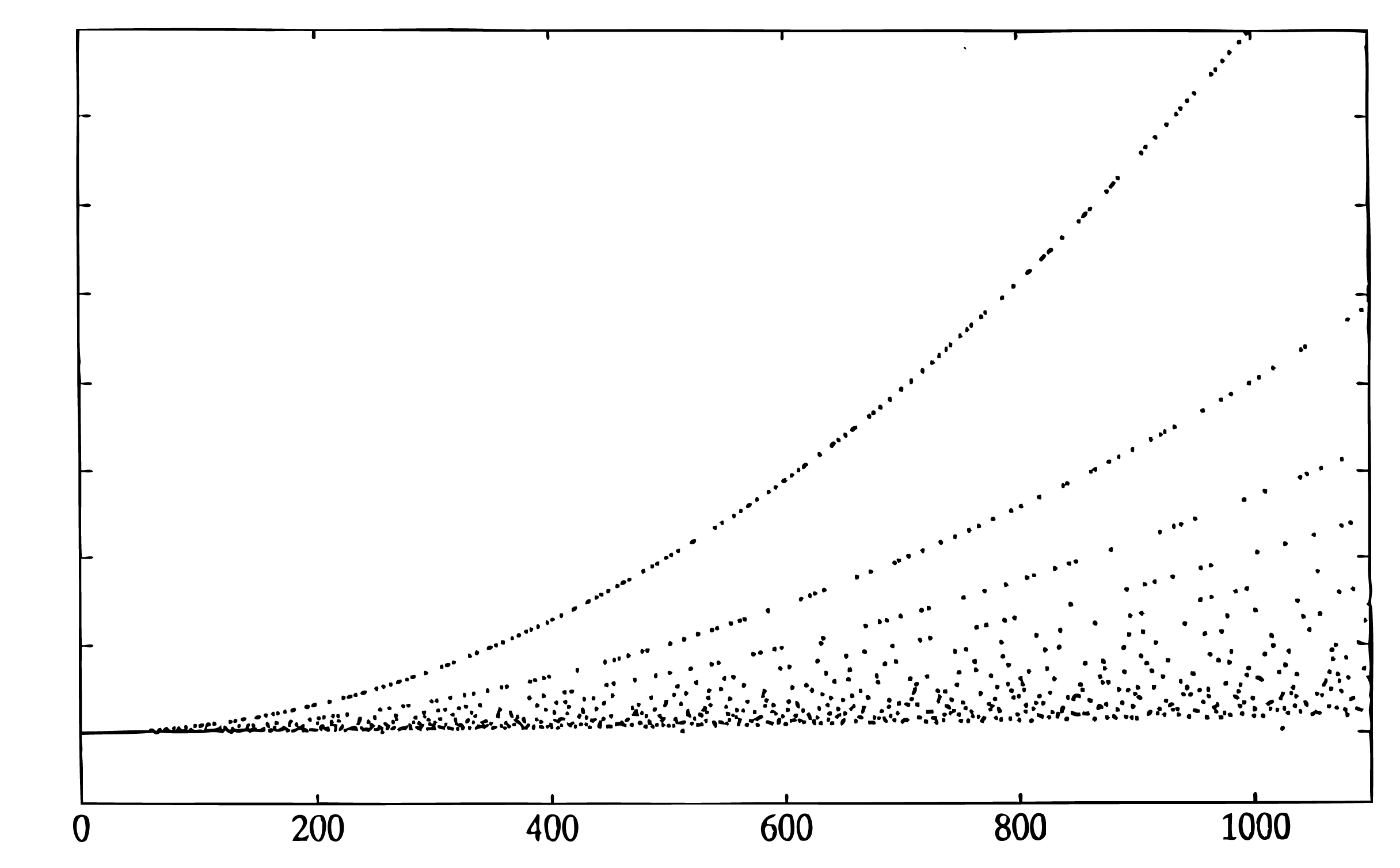
Fig. 14.2.1 Recuento de Flop vs Largo para la FFT Glassman-Ferguson

Anote la forma parabólica de la curva para ciertos valores. La curva superior es para longitudes primos, la siguiente es para longitudes que son dos veces una prima, y la siguiente es para longitudes que son para tres veces una prima, etc. La forma del límite inferior es aproximadamente\(N\log N\). El programa que generó estas dos cifras utilizó una FFT de Cooley-Tukey si la longitud es de dos a una potencia que da cuenta de los puntos que están por debajo del límite inferior mayor.

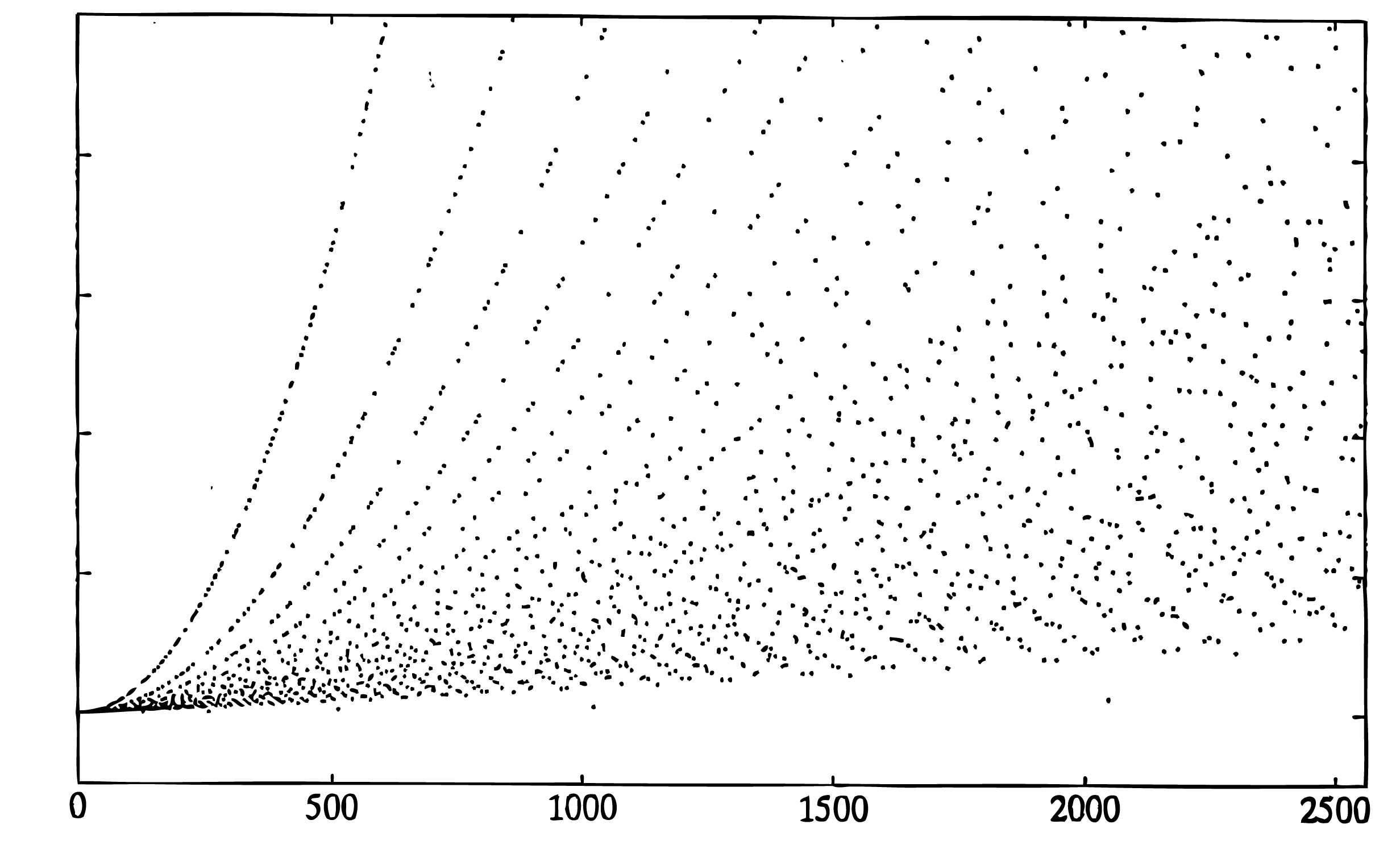
Fig. 14.2.1 Recuento de Flop vs Largo para la FFT Glassman-Ferguson

Colaborador

• ContribeeBurrus