4.1: Funciones definidas por piezas

En preparación para la definición de la función de valor absoluto, es extremadamente importante tener una buena comprensión del concepto de una función definida por partes. Sin embargo, antes de saltar a la refriega, echemos un vistazo a un tipo especial de función llamada función constante.

Una forma de entender una función constante es echar un vistazo a su gráfica.

Ejemplo\(\PageIndex{1}\)

Dibuje la gráfica de la función constante f (x) = 3.

Solución

Debido a que la notación f (x) = 3 es equivalente a la notación y = 3, podemos esbozar una gráfica de f dibujando la gráfica de la línea horizontal que tiene la ecuación y = 3, como se muestra en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\). La gráfica de una función constante es una línea horizontal.

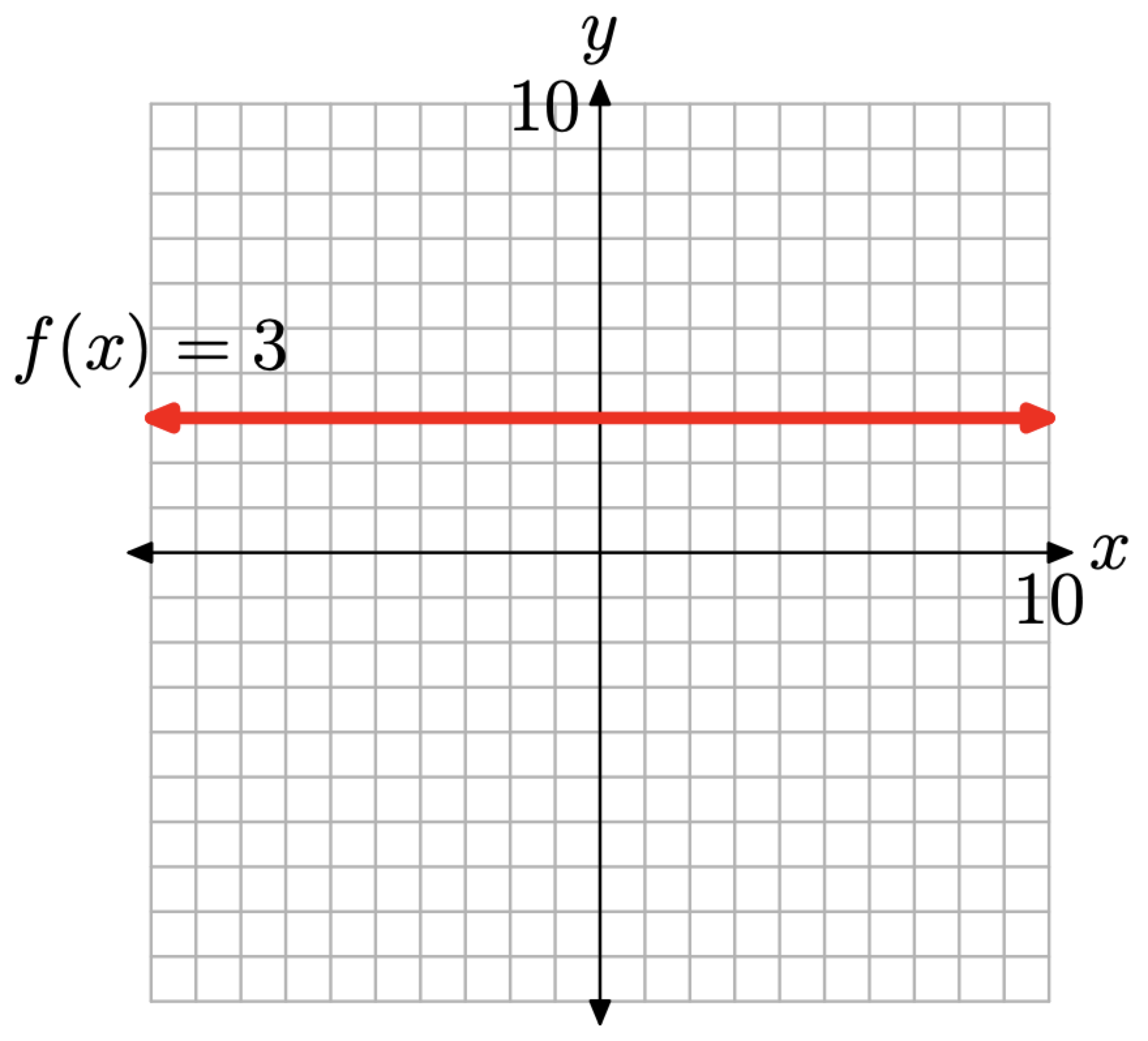
Cuando mire la gráfica de la Figura 1, tenga en cuenta que cada punto de la línea horizontal que tiene la ecuación f (x) = 3 tiene un valor y igual a 3. Decimos que los valores y en esta línea horizontal son constantes, por la simple razón de que son constantemente iguales a 3.

La forma de función funciona precisamente de la misma manera. Mira de nuevo la notación\[f(x)=3\]

Tenga en cuenta que no importa qué número sustituya por x en el lado izquierdo de f (x) = 3, el lado derecho es constantemente igual a 3. Así,

\[f(-5)=3, \quad f(-1 / 2)=3, \quad f(\sqrt{2})=3, \quad \text { or } \quad f(\pi)=3\]

La discusión anterior lleva a la siguiente definición.

Definición

La función definida por f (x) = c, donde c es una constante (número real fijo), se denomina función constante.

Dos comentarios están en orden:

1. f (x) = c para todos los números reales x.
2. La gráfica de f (x) = c es una línea horizontal. Consiste en todos los puntos (x, y) que tienen un valor y igual a c.

Funciones constantes por partes

Las funciones por pieza son las favoritas de los ingenieros. Veamos un ejemplo.

Ejemplo\(\PageIndex{2}\)

Supongamos que una batería no proporciona voltaje a un circuito cuando un interruptor está abierto. Entonces, comenzando en el momento\(t = 0\), el interruptor se cierra y la batería proporciona una constante de 5 voltios a partir de ese momento en adelante. Cree una función por partes que modele las restricciones del problema y esboce su gráfica.

Solución

Este es un ejercicio bastante sencillo, pero tendremos que introducir alguna notación nueva. En primer lugar, si el tiempo t es menor que cero (\(t < 0\)), entonces el voltaje es de 0 voltios. Si el tiempo t es mayor o igual a cero (\(t \geq 0\)), entonces el voltaje es una constante de 5 voltios. Aquí está la notación que usaremos para resumir esta descripción del voltaje.

\[V(t)=\left\{\begin{array}{ll}{0,} & {\text { if } t<0} \\ {5,} & {\text { if } t \geq 0}\end{array}\right.\]

Algunos comentarios están en orden:

• La diferencia de voltaje que proporciona la batería en el circuito es una función del tiempo. Así, V (t) representa el voltaje en el tiempo t.
• La notación utilizada en (4) es universalmente adoptada por los matemáticos en situaciones en las que la función cambia de definición dependiendo del valor de la variable independiente. Esta definición de la función V se denomina “definición por partes”. Debido a que cada una de las piezas en esta definición es constante, la función V se denomina función constante por partes.
• Esta función particular tiene dos piezas. La función es la función constante\(V (t) = 0\), cuándo\(t < 0\), pero una función constante diferente,\(V (t) = 5\), cuándo\(t \geq 0\).

Si\(t<0, V(t)=0 .\) Por ejemplo, para\(t=-1, t=-10,\) y\(t=-100\)

\[V(-1)=0, \quad V(-10)=0, \quad \text { and } \quad V(-100)=0\]

Por otro lado, si\(t \geq 0,\) entonces\(V(t)=5 .\) Por ejemplo, para\(t=0, t=10,\) y\(t=100\)

\[V(0)=5, \quad V(10)=5, \quad \text { and } \quad V(100)=5\]

Antes de presentar la gráfica de la función constante por partes V, hagamos una pausa por un momento para asegurarnos de entender algunos términos geométricos estándar.

Términos geométricos

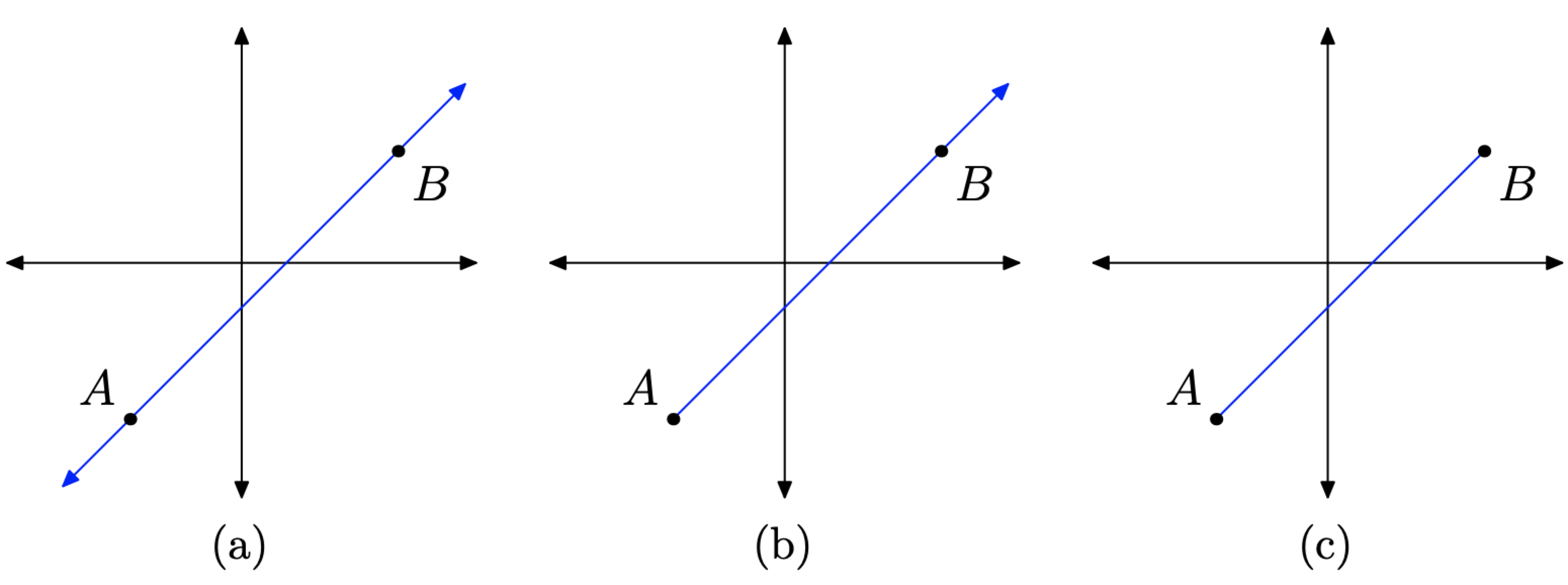
• Una línea se extiende indefinidamente en dos direcciones, como se muestra en la Figura\(\PageIndex{2}\) (a).
• Si una línea tiene un punto final fijo y se estira indefinidamente en una sola dirección, como se muestra en la Figura\(\PageIndex{2}\) (b), entonces se llama rayo.
• Si una porción de la línea está fija en cada extremo, como se muestra en la Figura\(\PageIndex{2}\) (c), entonces se denomina segmento de línea.

Figura\(\PageIndex{2}\). Líneas, rayos y segmentos.

Con estos términos en la mano, volvamos nuestra atención a la gráfica de la tensión definida por la ecuación (4). Cuando\(t < 0\), entonces\(V (t) = 0\). Normalmente, la gráfica de\(V (t) = 0\) sería una línea horizontal donde cada punto de la línea tiene V -valor igual a cero. No obstante,\(V (t) = 0\) sólo si\(t < 0\), así la gráfica es el rayo horizontal que inicia en el origen, entonces se mueve indefinidamente hacia la izquierda, como se muestra en la Figura\(\PageIndex{3}\). Es decir, la línea horizontal se\(V = 0\) ha restringido al dominio\(\{t : t<0\}\) y existe sólo a la izquierda del origen.

De igual manera, cuando\(t \geq 0\), entonces\(V (t) = 5\) es el rayo horizontal que se muestra en la Figura\(\PageIndex{3}\). Cada punto del rayo tiene un valor V igual a 5.

Figura\(\PageIndex{3}\). El voltaje en función del tiempo t.

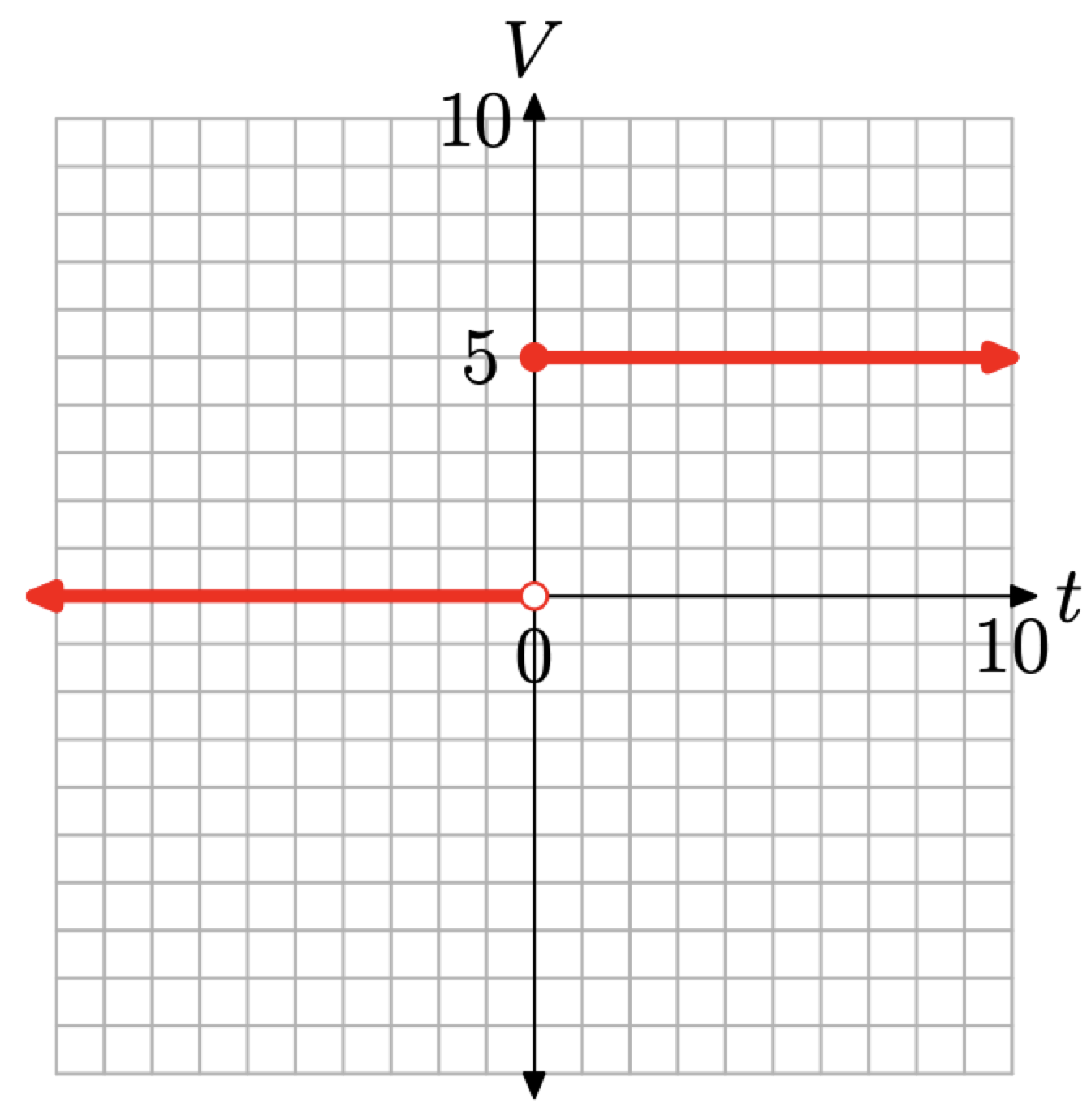
Dos comentarios están en orden:

• Porque\(V (t) = 0\) sólo cuando t < 0, el punto (0, 0) está sin rellenar (es un círculo abierto). El círculo abierto en (0, 0) es la manera de un matemático de decir que este punto en particular no está trazado ni sombreado.
• Porque\(V (t) = 5\) cuando\(t \geq 0\), el punto (0, 5) se llena (es un círculo relleno). El círculo relleno en (0, 5) es la manera de un matemático de decir que este punto en particular está trazado o sombreado.

Veamos otro ejemplo.

Ejemplo\(\PageIndex{3}\)

Considere la función definida por partes

\[f(x)=\left\{\begin{array}{ll}{0,} & {\text { if } x<0} \\ {1,} & {\text { if } 0 \leq x<2} \\ {2,} & {\text { if } x \geq 2}\end{array}\right.\]

Evalúa f (x) en x = −1, 0, 1, 2 y 3. Dibuje el gráfico de la función por partes f.

Solución

Debido a que cada pieza de la función en (6) es constante, la evaluación de la función es bastante fácil. Solo tienes que seleccionar la pieza correcta.

• Tenga en cuenta que x = −1 es menor que 0, así que usamos la primera pieza y escribimos f (−1) = 0.

• Tenga en cuenta que x = 0 satisface\(0 \leq x<2\), por lo que usamos la segunda pieza y escribimos f (0) = 1.

• Tenga en cuenta que x = 1 satisface\(0 \leq x<2\), por lo que usamos la segunda pieza y escribimos f (1) = 1.

• Tenga en cuenta que x = 2 satisface\(x \geq 2\), por lo que usamos la tercera pieza y escribimos f (2) = 2.

• Por último, tenga en cuenta que x = 3 satisface\(x \geq 2\), por lo que usamos la tercera pieza y escribimos f (3) = 2. El gráfico es igual de sencillo de esbozar.

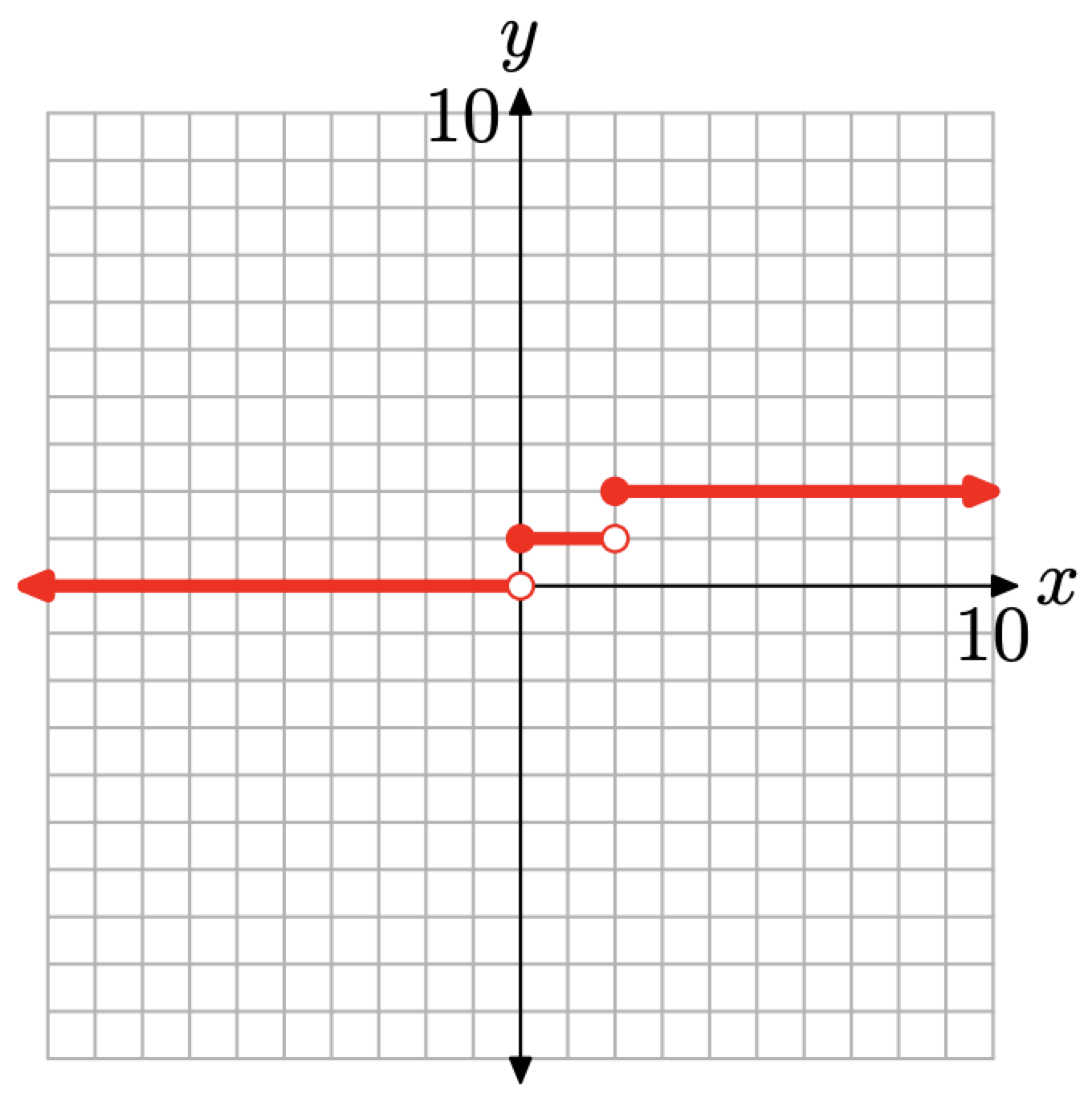
• Debido a que f (x) = 0 para x < 0, la gráfica de esta pieza es un rayo horizontal con punto final en x = 0. Cada punto de este rayo tendrá un valor y igual a cero y el rayo quedará completamente a la izquierda de x = 0, como se muestra en la Figura\(\PageIndex{4}\).

• Debido a que f (x) = 1 for\(0 \leq x<2\), la gráfica de esta pieza es un segmento horizontal con un punto final en x = 0 y el otro en x = 2. Cada punto de este segmento tendrá un valor y igual a 1, como se muestra en la Figura\(\PageIndex{4}\).

• Debido a que f (x) = 2 for\(x \geq 2\), la gráfica de esta pieza es un rayo horizontal con punto final en x = 2. Cada punto de este rayo tiene un valor y igual a 2 y el rayo se encuentra completamente a la derecha de x = 2, como se muestra en la Figura\(\PageIndex{4}\).

Varias observaciones están en orden:

• La función es cero a la izquierda del origen (para x < 0), pero no en el origen. Esto se indica mediante un círculo vacío en el origen, una indicación de que no estamos trazando ese punto en particular.

• Para\(0 \leq x<2\), la función es igual a 1. Es decir, la función es constantemente igual a 1 para todos los valores de x entre 0 y 2, incluyendo cero pero sin incluir 2. Es por esto que ves un círculo relleno en (0, 1) y un círculo vacío en (2, 1).

• Finalmente, for\(x \geq 2\), la función es igual a 2. Es decir, la función es constantemente igual a 2 siempre que x sea mayor o igual a 2. Es por eso que ves un círculo lleno en (2, 2).

Figura\(\PageIndex{4}\). Dibujando la gráfica de la función por partes (6).

Funciones definidas por piezas

Ahora, veamos una situación más genérica que involucra funciones definidas poco a poco, una en la que las piezas no son necesariamente constantes. La mejor manera de aprender es haciendo, así que comencemos con un ejemplo.

Ejemplo\(\PageIndex{4}\)

Considere la función definida por partes

\[f(x)=\left\{\begin{array}{ll}{-x+2,} & {\text { if } x<2} \\ {x-2,} & {\text { if } x \geq 2}\end{array}\right.\]

Evalúe f (x) para x = 0, 1, 2, 3 y 4, luego dibuje la gráfica de la función definida por partes.

Solución

La función cambia de definición en x = 2. Si x < 2, entonces f (x) = −x + 2. Debido a que tanto 0 como 1 son estrictamente menores que 2, evaluamos la función con esta primera pieza de la definición.

\[\begin{array}{ll}{f(x)=-x+2} &\text{and} & {f(x)=-x+2} \\ {f(0)=-0+2} & &{f(1)=-1+2} \\ {f(0)=2} & &{f(1)=1}\end{array}\]

Por otro lado, si\(x \geq 2\), entonces\(f(x) = x − 2\). Debido a que 2, 3 y 4 son todos mayores o iguales a 2, evaluamos la función con esta segunda pieza de la definición.

\[\begin{array}{lll}{f(x)=x-2}&{\text { and }} & {f(x)=x-2} & {\text { and }} & {f(x)=x-2} \\ {f(2)=2-2} &{\text { and }}& {f(3)=3-2} &{\text { and }}& {f(4)=4-2} \\ {f(2)=0} &{\text { and }}& {f(3)=1} & {\text { and }}&{f(4)=2}\end{array}\]

Una posible aproximación a la gráfica de f es colocar los puntos que ya calculamos, más un par extra, en una tabla (ver Figura\(\PageIndex{5}\) (a)), trazarlos (ver Figura\(\PageIndex{5}\) (b)), luego intuir la forma de la gráfica a partir de la evidencia proporcionada por los puntos trazados. Esto se hace en la Figura\(\PageIndex{5}\) (c).

Figura\(\PageIndex{5}\). Trazando la gráfica de la función por partes definida en (8).

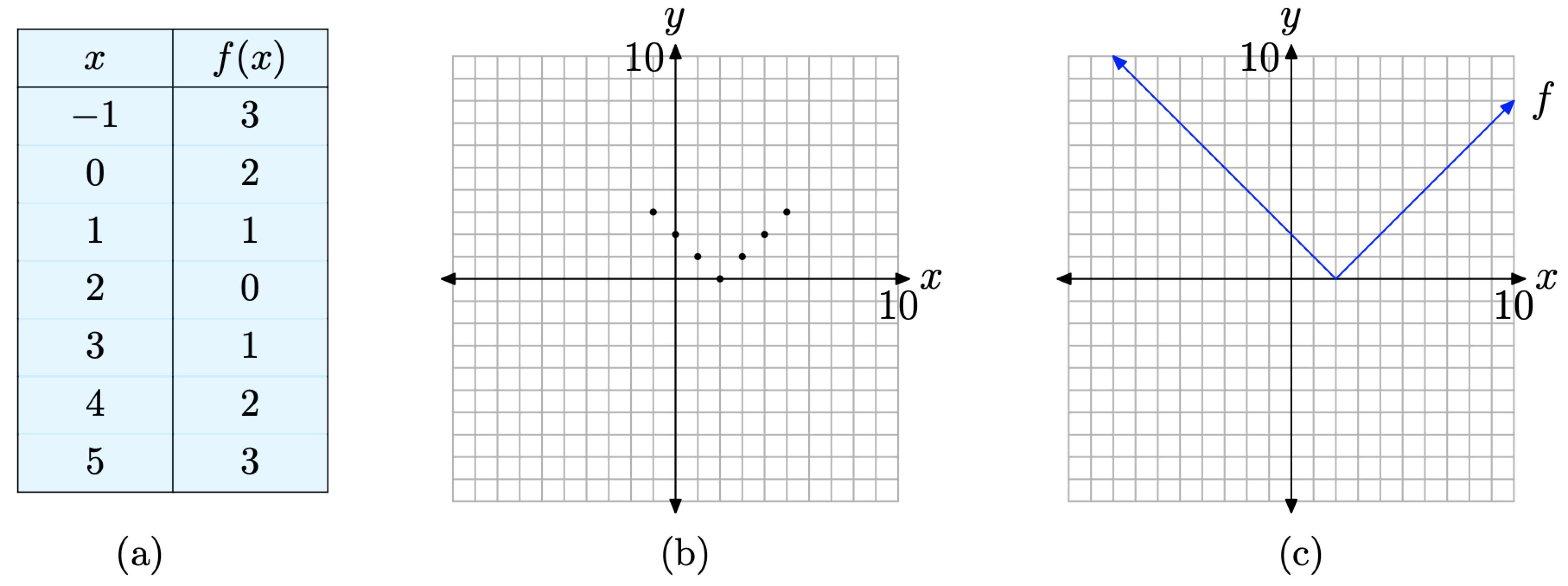
Por pragmático que sea, este enfoque de trazado de puntos es un poco tedioso; pero, lo que es más importante, no proporciona los antecedentes necesarios para la discusión de la función de valor absoluto en la siguiente sección. Necesitamos estirar nuestro entendimiento a un nivel superior. Afortunadamente, todo el trabajo de base está en su lugar. Solo necesitamos aplicar lo que ya sabemos sobre las ecuaciones de líneas para encajar esta situación por partes.

Enfoque alternativo. Usemos nuestro conocimiento de la ecuación de una línea (es decir, y = mx + b) para ayudar a bosquejar la gráfica de la función por partes definida en (8).

Vamos a esbozar la primera pieza de la función f definida en (8). Tenemos f (x) = −x+ 2, siempre x < 2. Normalmente, esta sería una línea (con pendiente −1 e intercepción 2), pero vamos a esbozar solo una parte de esa línea, la parte donde x < 2 (x está a la izquierda de 2). Así, esta pieza de la gráfica será un rayo, comenzando en el punto donde x = 2, luego moviéndose indefinidamente hacia la izquierda.

La forma más fácil de dibujar un rayo es primero calcular y trazar su punto final fijo (en este caso en x = 2), luego trazar un segundo punto en el rayo que tenga un valor x menor que 2, luego use una regla para dibujar el rayo.

Con este pensamiento en mente, para encontrar las coordenadas del punto final del rayo, sustituya x = 2 en f (x) = −x + 2 para obtener f (2) = 0. Ahora, técnicamente, no se supone que usemos esta pieza de la función a menos que x sea estrictamente menor que 2, pero podríamos usarlo con x = 1.9, o x = 1.99, o x = 1.999, etc. Así que sigamos adelante y usemos x = 2 en esta pieza de la función, pero indicamos que en realidad no se supone que utilicemos este punto dibujando un” círculo vacío” en (2, 0), como se muestra en la Figura\(\PageIndex{6}\) (a).

Para completar la gráfica del rayo, necesitamos un segundo punto que se encuentre a la izquierda de su punto final en (2, 0). Tenga en cuenta que x = 0 está a la izquierda de x = 2. Evalúa f (x) = −x + 2 a x = 0 para obtener f (0) = −0 + 2 = 2. Esto nos da el segundo punto (0, 2), que trazamos como se muestra en la Figura\(\PageIndex{6}\) (a). Finalmente, dibuje el rayo con punto final en (2, 0) y segundo punto en (0, 2), como se muestra en la Figura\(\PageIndex{6}\) (a).

Figura\(\PageIndex{6}\). Esbozar cada pieza por separado

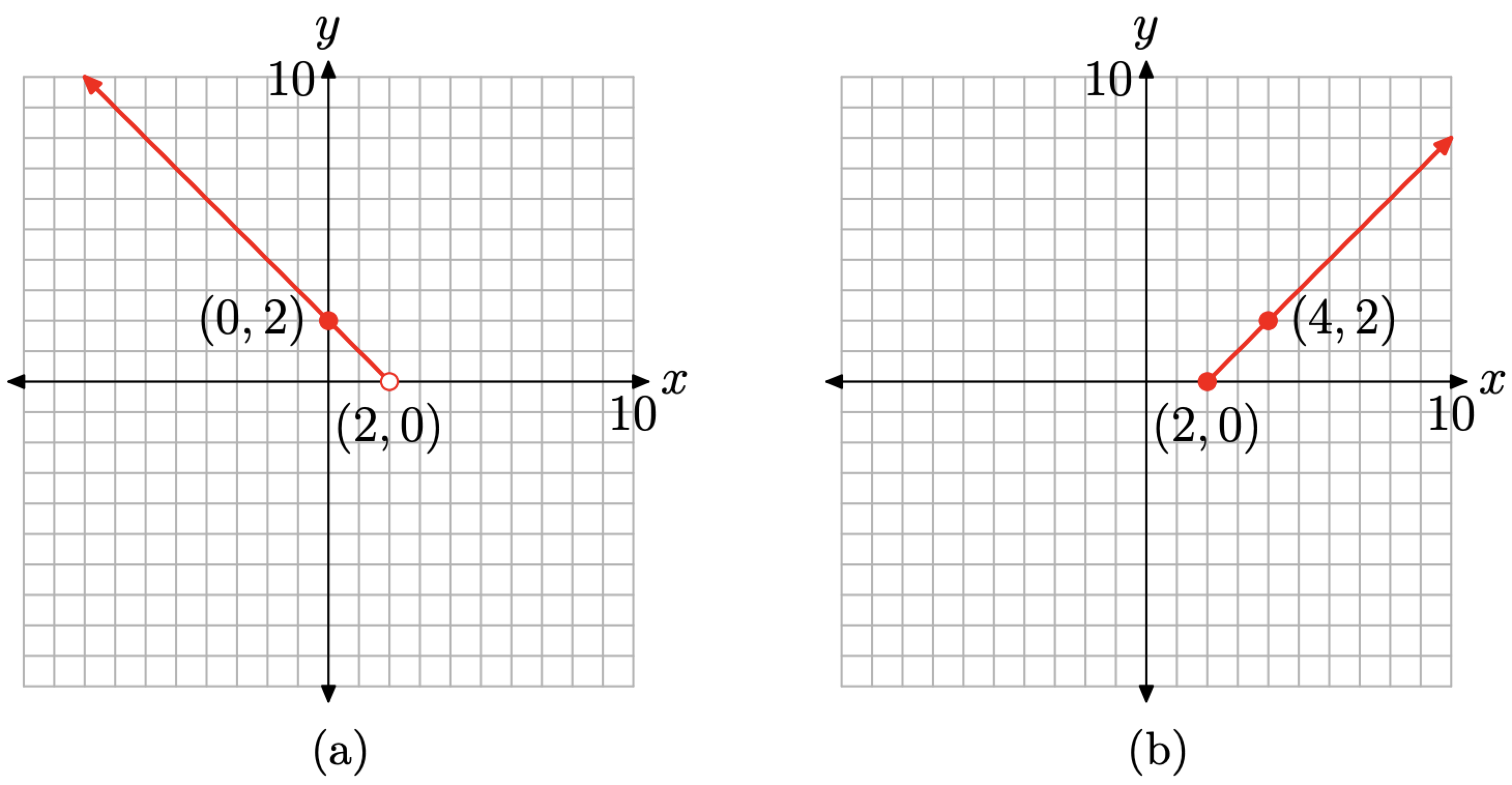
Ahora repetimos este proceso para la segunda pieza de la función definida en (8). La ecuación de la segunda pieza es f (x) = x − 2, proporcionada\(x \geq 2\). Normalmente, f (x) = x − 2 sería una línea (con pendiente 1 e intercepción −2), pero solo se supone que debemos esbozar esa parte de la línea que se encuentra a la derecha de o en x = 2. Así, la gráfica de esta segunda pieza es un rayo, comenzando en el punto con x = 2 y continuando hacia la derecha. Si evaluamos f (x) = x − 2 a x = 2, entonces f (2) = 2 − 2 = 0. Así, el punto final fijo del rayo está en el punto (2, 0). Como en realidad se supone que debemos usar esta pieza con x = 2, indicamos este hecho con un círculo relleno en (2, 0), como se muestra en la Figura\(\PageIndex{6}\) (b).

Necesitamos un segundo punto a la derecha de este punto final fijo, por lo que evaluamos f (x) = x−2 en x = 4 para obtener f (4) = 4 − 2 = 2. Así, un segundo punto en el rayo es el punto (4, 2). Finalmente, simplemente dibujamos el rayo, comenzando en el punto final (2, 0) y pasando por el segundo punto en (4, 2), como se muestra en la Figura\(\PageIndex{6}\) (b).

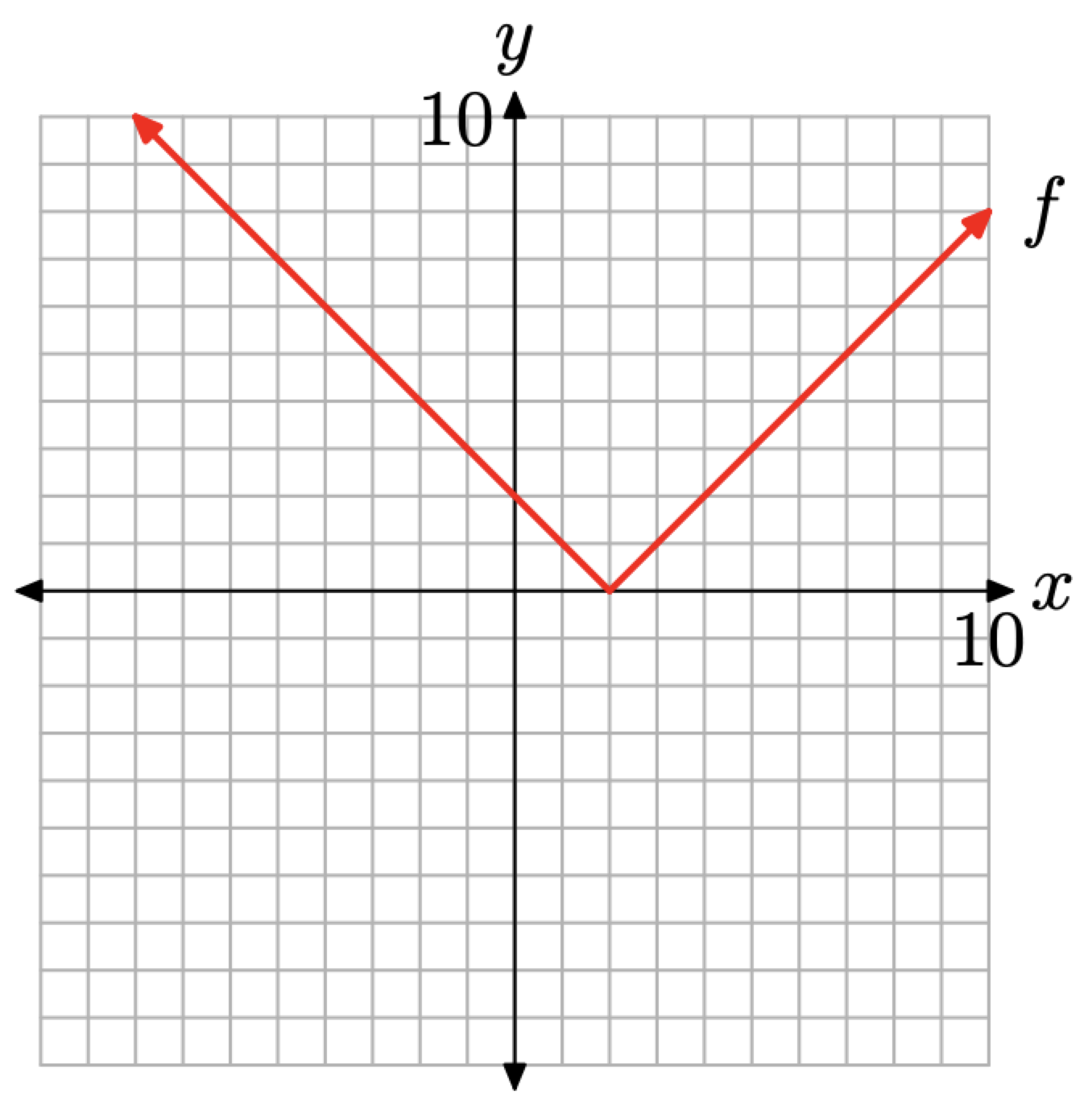
Para completar la gráfica de la función por partes f definida en la ecuación (8), simplemente combine las dos piezas en la Figura\(\PageIndex{6}\) (a) y Figura\(\PageIndex{6}\) (b) para obtener la gráfica terminada en la Figura\(\PageIndex{7}\). Obsérvese que la gráfica de la Figura\(\PageIndex{7}\) es idéntica al resultado anterior de la Figura\(\PageIndex{5}\) (c).

Probemos este procedimiento alternativo en otro ejemplo.

Ejemplo\(\PageIndex{5}\)

Una fuente proporciona voltaje a un circuito de acuerdo con la definición por tramos

\[V(t)=\left\{\begin{array}{ll}{0,} & {\text { if } t<0} \\ {t,} & {\text { if } t \geq 0}\end{array}\right.\]

Dibuje el gráfico de la tensión V versus tiempo t.

Solución

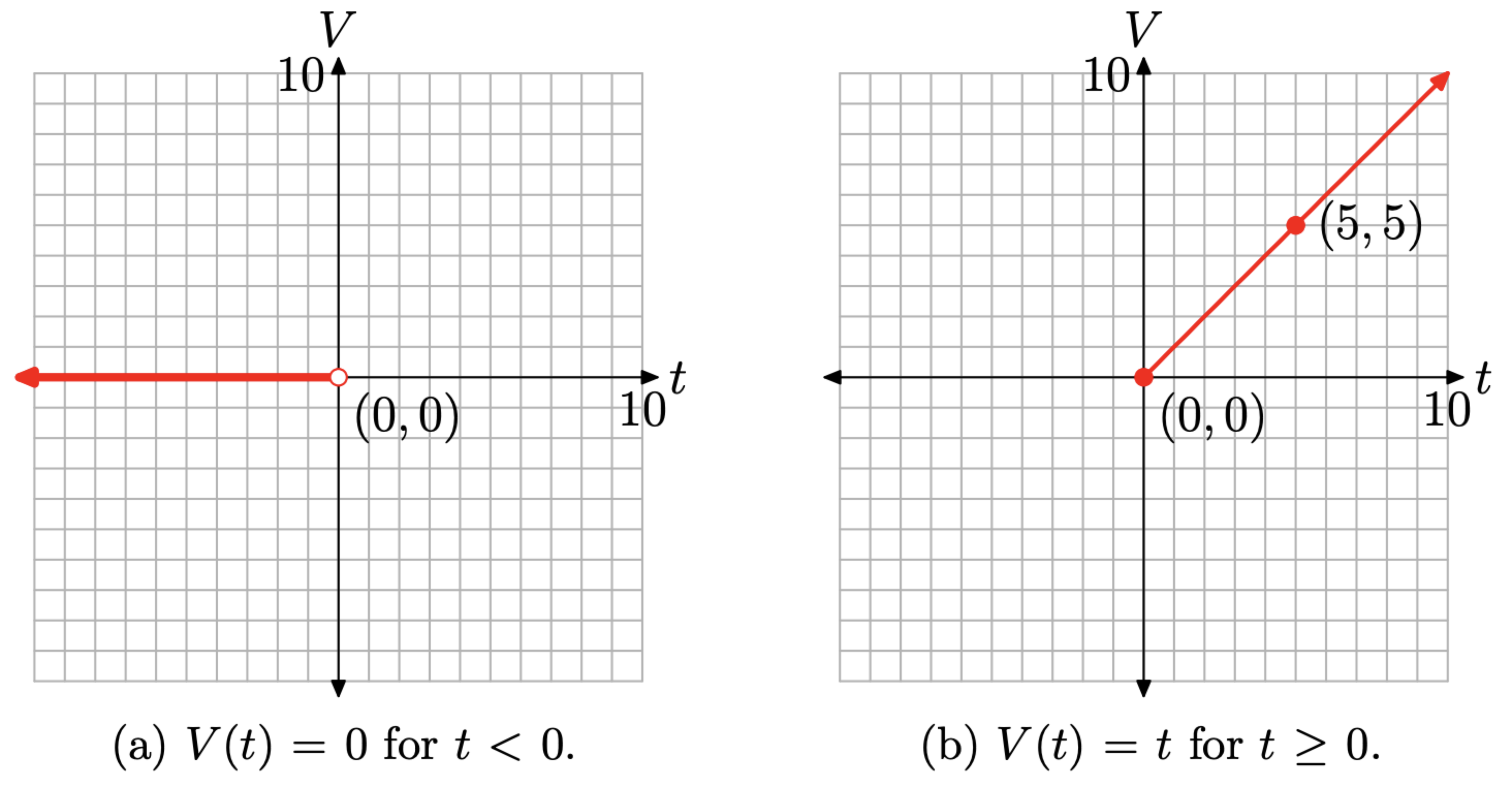
Para todos los tiempos t que sea menor a cero, el voltaje V es cero. La gráfica de V (t) = 0 es una función constante, por lo que su gráfica es normalmente una línea horizontal. Sin embargo, debemos restringir

Figura\(\PageIndex{7}\). Combinando ambas piezas.

la gráfica al dominio\((-\infty, 0)\), por lo que esta pieza de ecuación (10) será un rayo horizontal, comenzando en el origen y moviéndose indefinidamente hacia la izquierda, como se muestra en la Figura\(\PageIndex{8}\) (a).
Por otro lado, V (t) = t para todos los valores de t que sean mayores o iguales a cero. Normalmente, esta sería una línea con pendiente 1 e interceptar cero. No obstante, debemos restringir el dominio a\([0, \infty)\), por lo que esta pieza de ecuación (10) será un rayo, comenzando en el origen y moviéndose indefinidamente hacia la derecha.

• El punto final de este rayo comienza en t = 0. Porque V (t) = t, V (0) = 0. De ahí que el punto final de este rayo esté en el punto (0, 0).
• Elija cualquier valor de t que sea mayor que cero. Escogeremos t = 5. Porque V (t) = t, V (5) = 5. Esto nos da un segundo punto sobre el rayo en (5, 5), como se muestra en la Figura\(\PageIndex{8}\) (b).

Figura\(\PageIndex{8}\).

Finalmente, para proporcionar una gráfica completa de la función de voltaje definida por la ecuación (10), combinamos las gráficas de cada pieza de la definición mostrada en las Figuras\(\PageIndex{8}\) (a) y (b).

El resultado se muestra en la Figura\(\PageIndex{9}\). Los ingenieros se refieren a este tipo de función de entrada como una “función de rampa”.

Figura\(\PageIndex{9}\). La gráfica de la función de rampa definida por la ecuación (10).

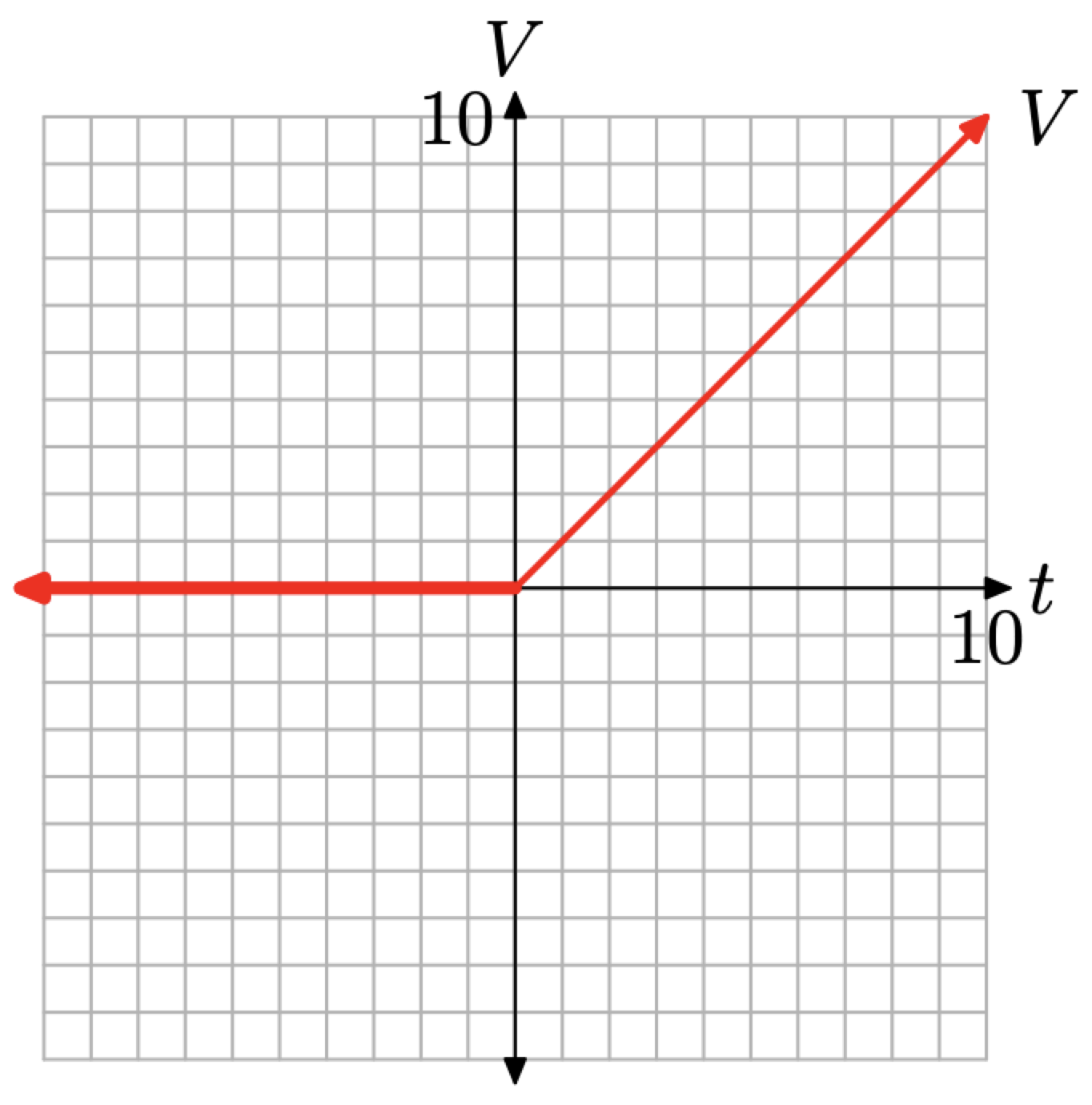
Veamos una aplicación muy práctica de funciones por partes.

Ejemplo\(\PageIndex{6}\)

Las tasas del impuesto federal sobre la renta para un solo declarante en el año 2005 se dan en la Tabla\(\PageIndex{1}\).

Tabla\(\PageIndex{1}\). 2005 Tasas del Impuesto sobre la Renta de la Federación para declarante único.

Ingresos	Tasa impositiva
Hasta $7,150	10%
$7,151-$29,050	15%
29,051-$70,350	25%
$70,351 - $146,750	28%
$146,751- $319,100	33%
$319,101 o más	35%

Crear una definición fragmentada que proporcione la tasa impositiva en función de los ingresos personales.

Solución

Al informar los ingresos imponibles, los montos se redondean al dólar más cercano en el formulario de impuesto federal sobre la renta. Técnicamente, el dominio es discreto. Se puede reportar un ingreso imponible de $35,000 o $35,001, pero los números entre estos dos ingresos no se utilizan en el formulario de impuesto federal sobre la renta. No obstante, pensaremos en el ingreso como un continuo, permitiendo que el ingreso sea cualquier número real mayor o igual a cero. Si no lo hiciéramos, entonces nuestra gráfica sería una serie de puntos, uno por cada monto en dólares. ¡Tendríamos que trazar muchos puntos!

Dejaremos que R represente la tasa impositiva y yo represente los ingresos. El objetivo es definir R como una función de I.

• Si el ingreso I es cualquier cantidad mayor o igual a cero, e inferior o igual a $7,150, la tasa impositiva R es del 10% (es decir, R = 0.10). Por lo tanto\(\$ 0 \leq I \leq \$ 7,150\), si, R (I) = 0.10.
• Si el ingreso I es cualquier cantidad que sea estrictamente mayor a $7,150 pero menor o igual a $29,050, entonces la tasa impositiva R es del 15% (es decir, R = 0.15). Así, si $7, 150 < I ≤ $29, 050, entonces R (I) = 0.15.

Continuando de esta manera, podemos construir una definición fragmentada de tasa R en función de la renta imponible I.

\[R(I)=\left\{\begin{array}{ll}{0.10,} & {\text { if } \$ 0 \leq I \leq \$ 7,150} \\ {0.15,} & {\text { if } \$ 7,150<I \leq \$ 29,050} \\ {0.25,} & {\text { if } \$ 29,050<I \leq \$ 70,350} \\ {0.28,} & {\text { if } \$ 70,350<I \leq \$ 146,750} \\ {0.33,} & {\text { if } \$ 146,750<I \leq \$ 319,100} \\ {0.35,} & {\text { if } I>\$ 319,100}\end{array}\right.\]

Volvamos nuestra atención a la gráfica de esta función definida poco a poco. Todas las piezas son funciones constantes, por lo que cada pieza será una línea horizontal a un nivel que indique la tasa impositiva. Sin embargo, cada una de las primeras cinco piezas de la función definida en la ecuación (12) son segmentos, porque la tasa se define en un intervalo con un ingreso inicial y final. La sexta y última pieza es un rayo, ya que tiene un punto final inicial, pero la tasa se mantiene constante para todos los ingresos por encima de $319.100. Utilizamos este conocimiento para construir la gráfica que se muestra en la Figura\(\PageIndex{10}\).

La primera tasa es del 10% y ésta se asigna a la renta imponible a partir de $0 y terminando en $7,150, inclusive. Así, anote el primer segmento de línea horizontal en la Figura\(\PageIndex{10}\) que va de $0 a $7,150 a una altura de R = 0.10. Tenga en cuenta que cada uno de los puntos finales son círculos rellenos.

La segunda tasa es del 15% y ésta se asigna a ingresos imponibles mayores a $7,150, pero menores o iguales a $29,050. El segundo segmento de línea horizontal en la Figura 10 va desde $7,150 a $29,050 a una altura de R = 0.15. Tenga en cuenta que el punto final en el extremo izquierdo de este segmento horizontal es un círculo abierto mientras que el punto final en el extremo derecho es un círculo lleno porque los ingresos imponibles oscilan en $7, 150 < I ≤ $29, 050. Por lo tanto, excluimos el punto final izquierdo e incluimos el extremo derecho.

Los segmentos restantes se dibujan de manera similar.

La última pieza asigna una tasa de R = 0.35 a todos los ingresos imponibles estrictamente por encima de $319,100. De ahí que la última pieza sea un rayo horizontal, comenzando en ($319 100, 0.35) y extendiéndose indefinidamente hacia la derecha. Obsérvese que el punto final izquierdo de este rayo es un círculo abierto porque la tasa R = 0.35 se aplica a los ingresos imponibles I > $319, 100.

Hablemos un momento sobre el dominio y rango de la función R definida por la ecuación (12). La gráfica de R se representa en la Figura\(\PageIndex{10}\). Si proyectamos todos los puntos de la gráfica sobre el eje horizontal, todo el eje “quedará en la sombra”. Así, al principio

Figura\(\PageIndex{10}\). La gráfica de la tasa impositiva R versus la renta imponible I.

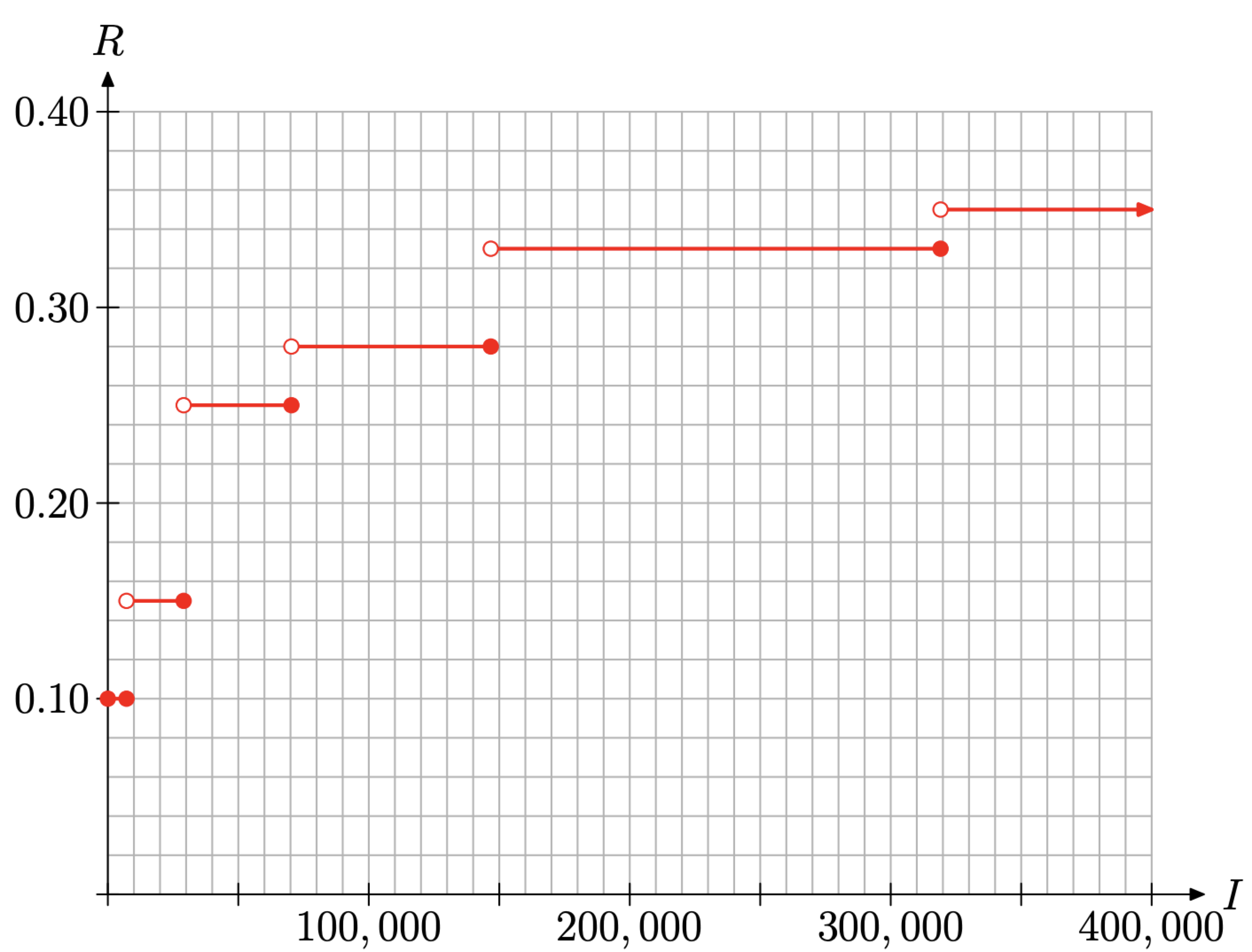
vistazo, se diría que el dominio de R es el conjunto de todos los números reales que son mayores o iguales a cero.

Sin embargo, recuerde que elegimos modelar una situación discreta con un continuo. Los ingresos imponibles siempre se redondean al dólar más cercano en los formularios de impuestos federales sobre la renta. Por lo tanto, el dominio es en realidad todos los números enteros mayores o iguales a cero. En símbolos,

\[\text { Domain }=\{I \in \mathbb{W} : I \geq 0\}\]

Para encontrar el rango de R, proyectaríamos todos los puntos de la gráfica de R en Figura\(\PageIndex{10}\) sobre el eje vertical. El resultado sería que seis puntos estarían sombreados en el eje vertical, uno cada uno a 0.10, 0.15, 0.25, 0.28, 0.33 y 0.35. Por lo tanto, el rango es un conjunto discreto finito, por lo que se describe mejor simplemente enumerando a sus miembros.

\[\text { Range }=\{0.10,0.15,0.25,0.28,0.33,0.35\}\]

Ejercicio

Ejercicio\(\PageIndex{1}\)

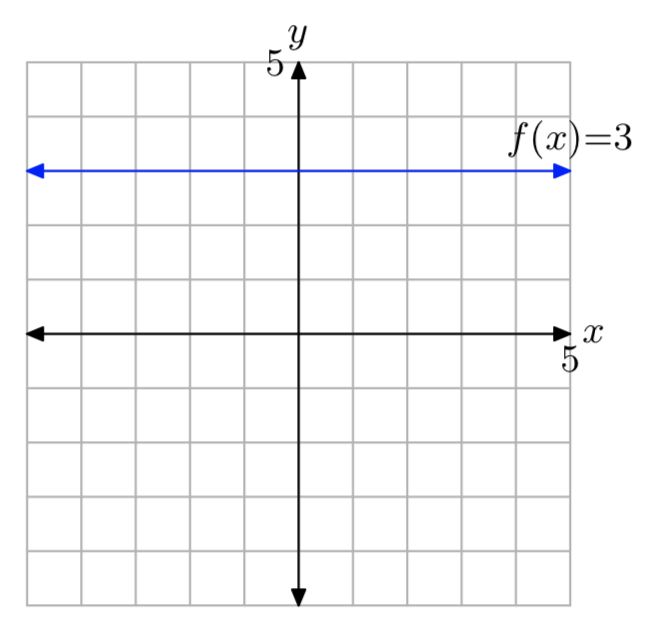
Dada la función definida por la regla f (x) = 3, evaluar f (−3), f (0) y f (4), luego esbozar la gráfica de f.

Contestar

f (−3) = 3, f (0) = 3 y f (4) = 3.

Ejercicio\(\PageIndex{2}\)

Dada la función definida por la regla g (x) = 2, evaluar g (−2), g (0) y g (4), luego dibujar el dibujo la gráfica de g.

Ejercicio\(\PageIndex{3}\)

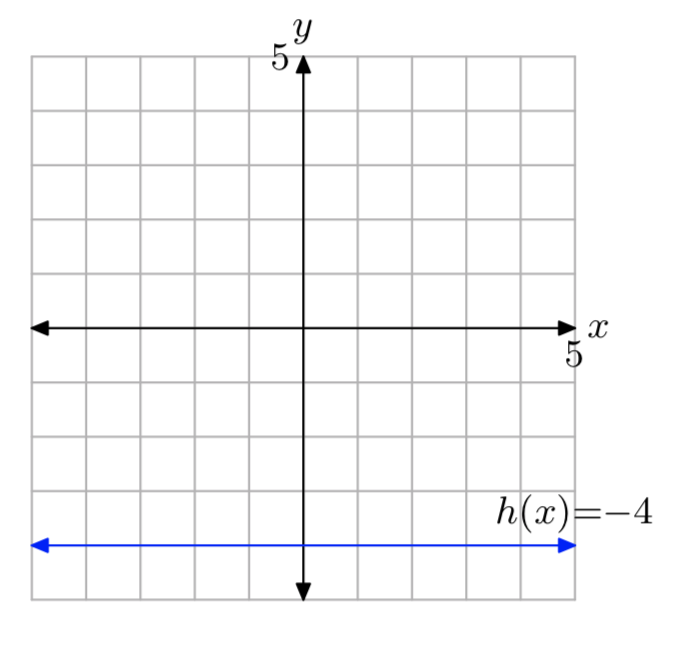
Dada la función definida por la regla h (x) = −4, evaluar h (−2), h (a) y h (2x+3), luego dibujar la gráfica de h.

Contestar

h (−2) = −4, h (a) = −4, y h (2x+3) = −4.

Ejercicio\(\PageIndex{4}\)

Dada la función definida por la regla f (x) = −2, evalúe f (0), f (b) y f (5−4x), luego dibuje la gráfica de f.

Ejercicio\(\PageIndex{5}\)

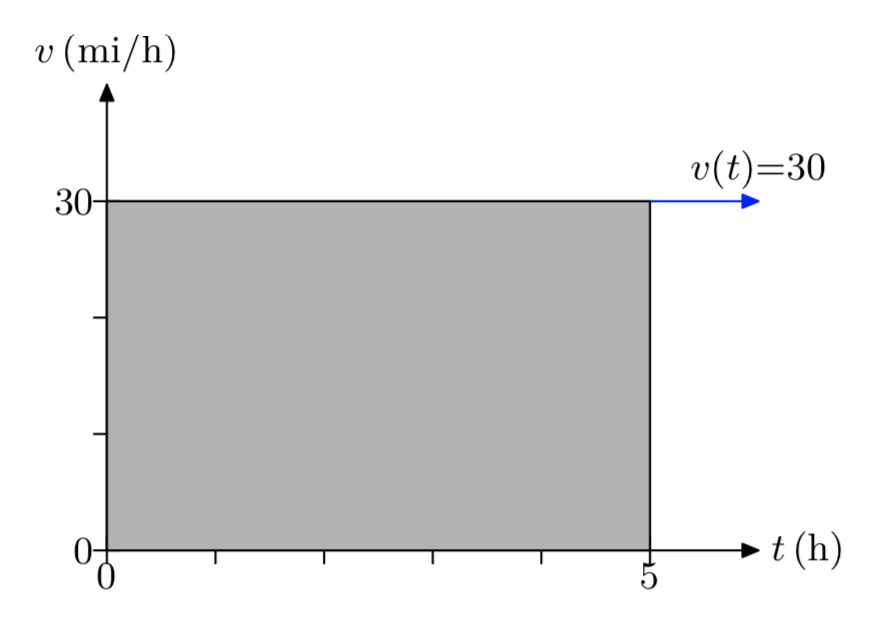
La velocidad de un automóvil que viaja en la carretera es función del tiempo y se describe por la función constante v (t) = 30, donde t se mide en horas y v se mide en millas por hora. Dibuja la gráfica de v versus t. Asegúrese de etiquetar cada eje con las unidades apropiadas. Sombra el área bajo la gráfica de v durante el intervalo de tiempo [0,5] horas. ¿Cuál es el área bajo la gráfica de v durante este intervalo de tiempo y qué representa?

Contestar

El área bajo la curva es de 150 millas. Esta es la distancia recorrida por el carro.

Ejercicio\(\PageIndex{6}\)

La velocidad de una patinadora mientras recorre una pendiente es función del tiempo y se describe por la función constante v (t) = 8, donde t se mide en segundos y v se mide en pies por segundo. Dibuja la gráfica de v versus t. Asegúrese de etiquetar cada eje con las unidades apropiadas. Sombra el área bajo la gráfica de v durante el intervalo de tiempo [0,60] segundos. ¿Cuál es el área bajo la gráfica de v durante este intervalo de tiempo y qué representa?

Ejercicio\(\PageIndex{7}\)

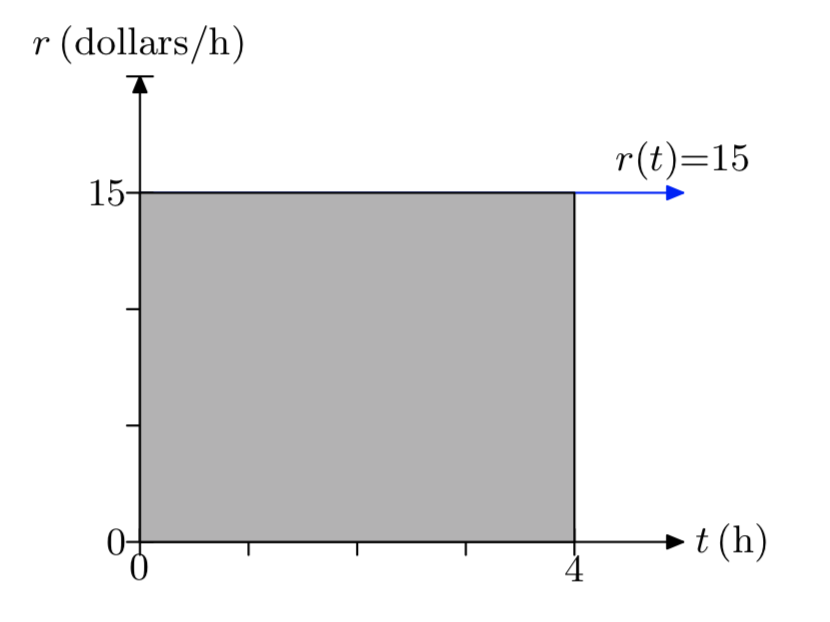
Un plomero sin licencia cobra 15 dólares por cada hora de mano de obra. Definamos esta tasa en función del tiempo por r (t) = 15, donde t se mide en horas y r se mide en dólares por hora. Dibuja la gráfica de r versus t. Asegúrese de etiquetar cada eje con las unidades apropiadas. Sombra el área bajo la gráfica de r durante el intervalo de tiempo [0,4] horas. ¿Cuál es el área bajo la gráfica de r durante este intervalo de tiempo y qué representa?

Contestar

El área bajo la curva es de 150 millas. Esta es la distancia recorrida por el carro.

Ejercicio\(\PageIndex{8}\)

Un carpintero cobra una tarifa fija por cada hora de mano de obra. Describamos esta tasa en función del tiempo por r (t) = 25, donde t se mide en horas y r se mide en dólares por hora. Dibuja la gráfica de r versus t. Asegúrese de etiquetar cada eje con las unidades apropiadas. Sombra el área bajo la gráfica de r durante el intervalo de tiempo [0, 5] horas. ¿Cuál es el área bajo la gráfica de r durante este intervalo de tiempo y qué representa?

Ejercicio\(\PageIndex{9}\)

Dada la función definida por la regla

\[f(x)=\left\{\begin{array}{ll}{0,} & {\text { if } x<0} \\ {2,} & {\text { if } x \ge 0} \nonumber \end{array}\right.\]

evaluar f (−2), f (0) y f (3), luego dibujar la gráfica de f en una hoja de papel cuadriculado. Declarar el dominio y rango de f.

Contestar

f (−2) = 0, f (0) = 2 y f (3) = 2.

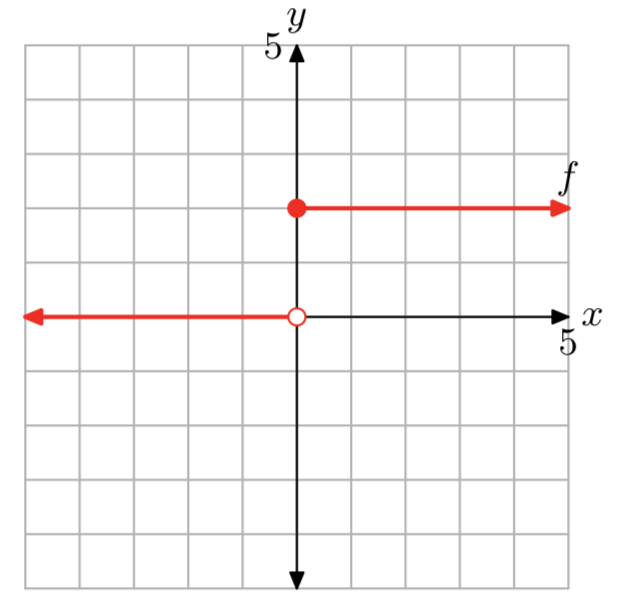
El dominio de f es el conjunto de todos los números reales. El rango de f es {0, 2}.

Ejercicio\(\PageIndex{10}\)

Dada la función definida por la regla

\[f(x)=\left\{\begin{array}{ll}{2,} & {\text { if } x<0} \\ {0,} & {\text { if } x \ge 0} \nonumber \end{array}\right.\]

evaluar f (−2), f (0) y f (3), luego dibujar la gráfica de f en una hoja de papel cuadriculado. Declarar el dominio y rango de f.

Ejercicio\(\PageIndex{11}\)

Dada la función definida por la regla

\[f(x)=\left\{\begin{array}{ll}{-3,} & {\text { if } x<0} \\ {1,} & {\text { if } -2 \le x < 2}\\ {3,} &{\text{ if } x \ge 2} \nonumber \end{array}\right.\]

evaluar g (−3), g (−2) y g (5), luego dibujar la gráfica de g en una hoja de papel cuadriculado. Declarar el dominio y el rango de g.

Contestar

g (−3) = −3, g (−2) = 1 y g (5) = 3

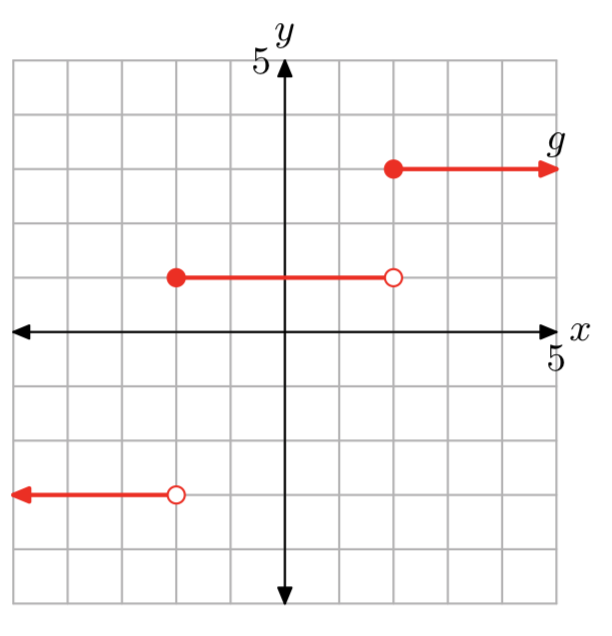
El dominio de g es todo números reales. El rango de g es {−3, 1, 3}.

Ejercicio\(\PageIndex{12}\)

Dada la función definida por la regla

\[f(x)=\left\{\begin{array}{ll}{4,} & {\text { if } x \le -1} \\ {2,} & {\text { if } -1 < x \le 2}\\ {-3,} &{\text{ if } x > 2} \nonumber \end{array}\right.\]

evaluar g (−1), g (2) y g (3), luego dibujar la gráfica de g en una hoja de papel cuadriculado. Declarar el dominio y el rango de g.

En los Ejercicios 13 - 16, determinar una definición por partes de la función descrita por las gráficas, luego indicar el dominio y el rango de la función.

Ejercicio\(\PageIndex{13}\)

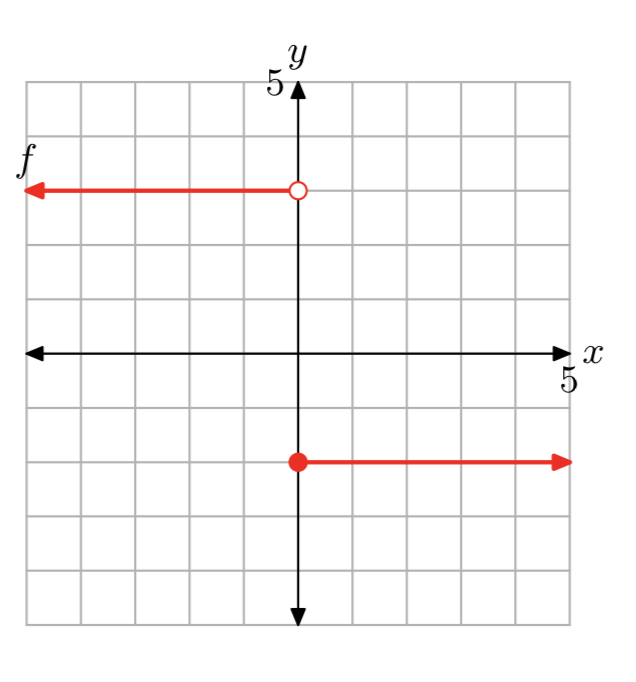
Contestar

\[f(x)=\left\{\begin{array}{ll}{3,} & {\text { if } x<0} \\ {-2,} & {\text { if } x \ge 0} \nonumber \end{array}\right.\]

Dominio de f es el conjunto de todos los números reales. El rango de f es {−2, 3}.

Ejercicio\(\PageIndex{14}\)

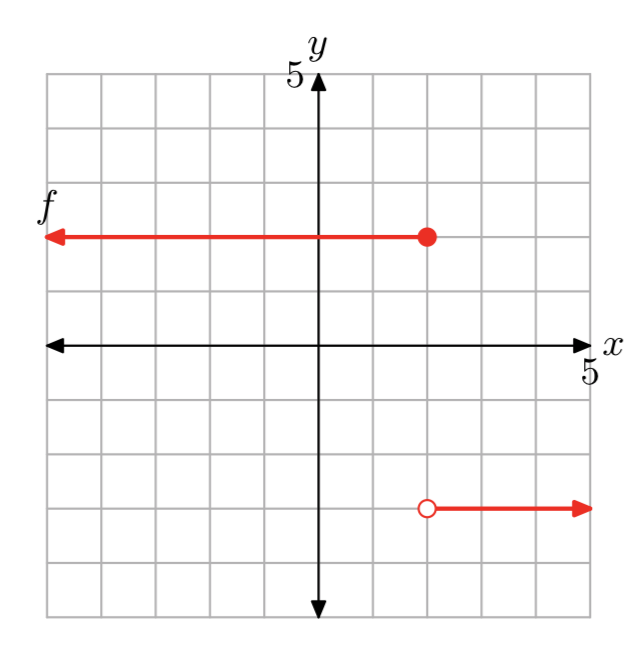
Ejercicio\(\PageIndex{15}\)

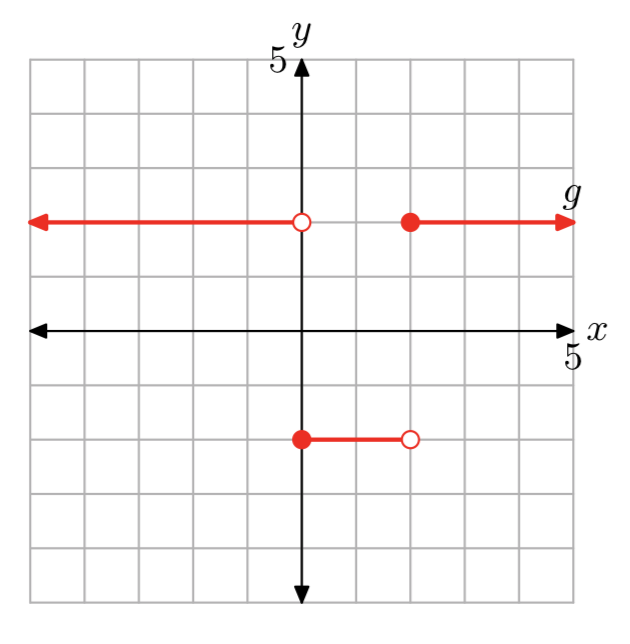
Contestar

\[g(x)=\left\{\begin{array}{ll}{2,} & {\text { if } x < 0} \\ {-2,} & {\text { if } 0 \le x < 2}\\ {2,} &{\text{ if } x > 2} \nonumber \end{array}\right.\]

El dominio de f es el conjunto de todos los números reales. El rango de f es {−2, 2}.

Ejercicio\(\PageIndex{16}\)

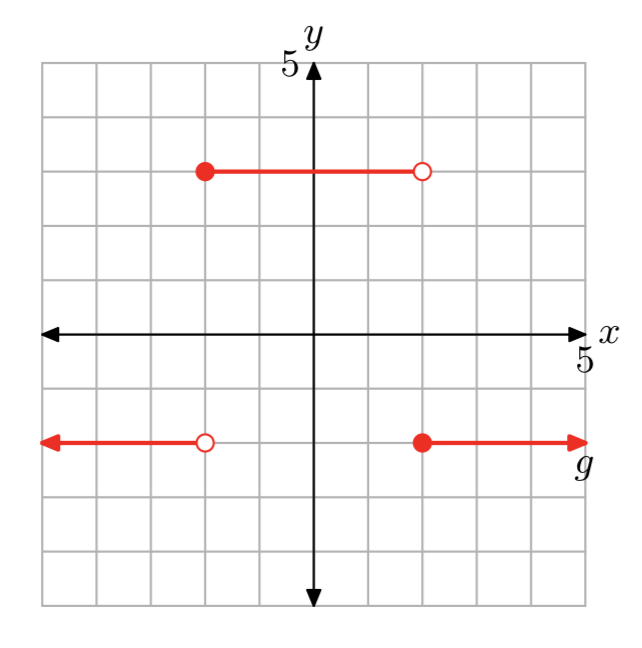
Ejercicio\(\PageIndex{17}\)

Dada la función por partes

\[f(x)=\left\{\begin{array}{ll}{-x-3,} & {\text { if } x<-3} \\ {x+3,} & {\text { if } x \ge -3} \nonumber \end{array}\right.\]

evaluar f (−4) y f (0), luego dibujar la gráfica de f en una hoja de papel cuadriculado. Indicar el dominio y el rango de la función.

Contestar

f (−4) = 1 y f (0) = 3.

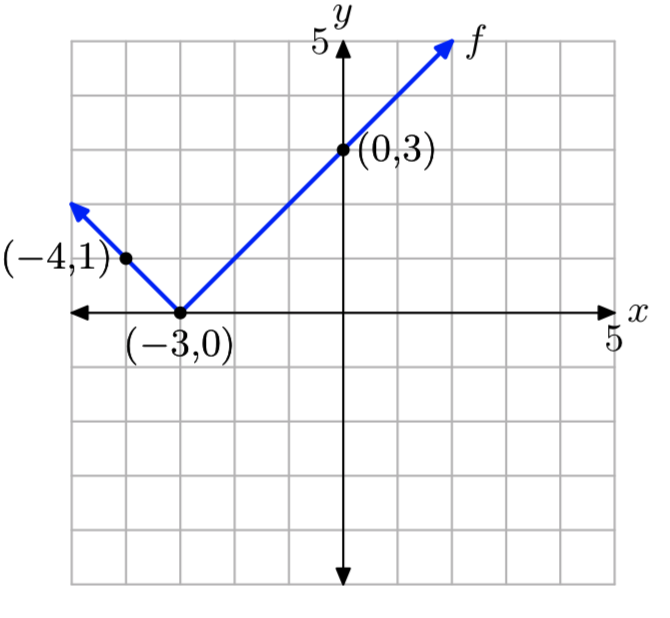
El dominio de f es el conjunto de todos los números reales. El rango desactivado es {y:\(y \ge 0\)}.

Ejercicio\(\PageIndex{18}\)

Dada la función por partes

\[f(x)=\left\{\begin{array}{ll}{-x+1,} & {\text { if } x<1} \\ {x-1,} & {\text { if } x \ge 1} \nonumber \end{array}\right.\]

evaluar f (−2) y f (3), luego dibujar la gráfica de f en una hoja de papel cuadriculado. Indicar el dominio y el rango de la función.

EXERICSE\(\PageIndex{19}\)

Dada la función por partes

\[g(x)=\left\{\begin{array}{ll}{-2x+3,} & {\text { if } x<\frac{3}{2}} \\ {2x-3,} & {\text { if } x \ge \frac{3}{2}} \nonumber \end{array}\right.\]

evaluar g (0) y g (3), luego dibujar la gráfica de f en una hoja de papel cuadriculado. Indicar el dominio y el rango de la función.

Contestar

g (−2) = 7 y g (2) = 1.

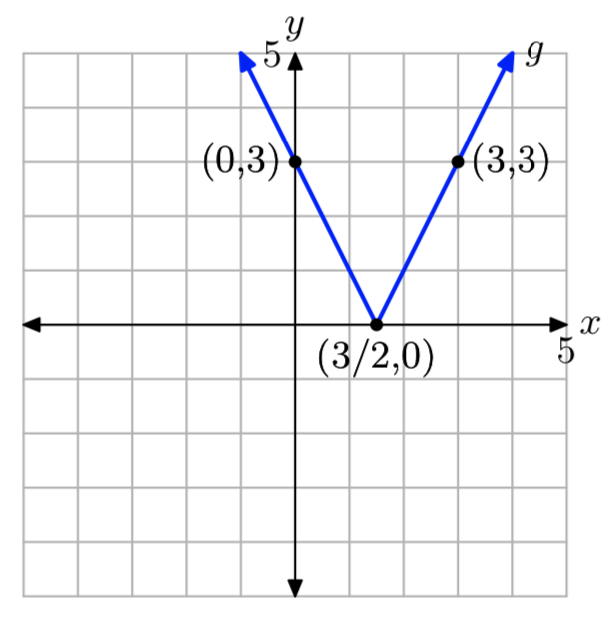
El dominio de g es el conjunto de todos los números reales. El rango desactivado es {y:\(y \ge 0\)}.

Ejercicio\(\PageIndex{20}\)

Dada la función por partes

\[g(x)=\left\{\begin{array}{ll}{-3x-4,} & {\text { if } x<-\frac{4}{3}} \\ {3x+4,} & {\text { if } x \ge -\frac{4}{3}} \nonumber \end{array}\right.\]

evaluar g (−2) y g (3), luego dibujar la gráfica de f en una hoja de papel cuadriculado. Indicar el dominio y el rango de la función.

Ejercicio\(\PageIndex{21}\)

Una batería suministra voltaje a un circuito eléctrico de la siguiente manera. Antes del tiempo t = 0 segundos, un interruptor está abierto, por lo que el voltaje suministrado por la batería es de cero voltios. En el tiempo t = 0 segundos, el interruptor se cierra y la batería comienza a suministrar una constante de 3 voltios al circuito. En el tiempo t = 2 segundos, el interruptor se abre de nuevo, y el voltaje suministrado por la batería cae inmediatamente a cero voltios. Esboce un gráfico del voltaje frente al tiempo t, etiquete cada eje con las unidades apropiadas, luego proporcione una definición por partes del voltaje v suministrado por la batería en función del tiempo t.

Contestar

A continuación se muestra la gráfica.

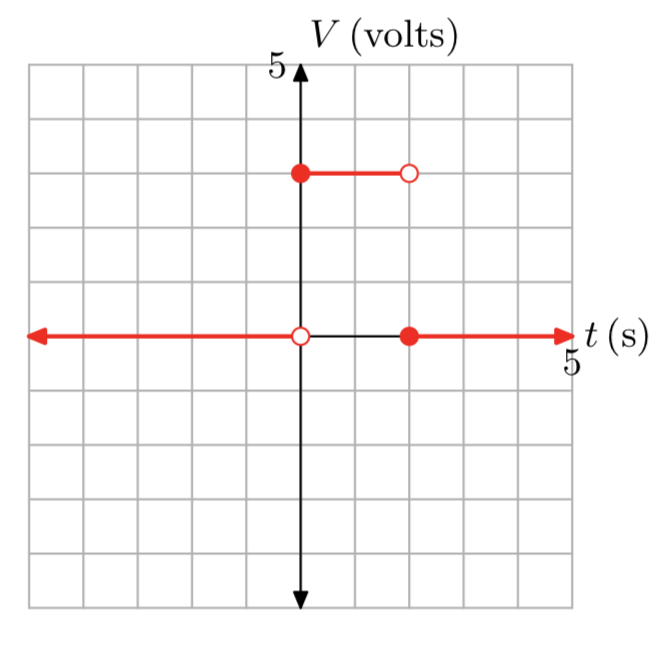
\[g(x)=\left\{\begin{array}{ll}{0,} & {\text { if } x<0} \\ {3,} & {\text { if } 0 \le x < 2}\\ {0,} & {\text{ if } x \ge 2} \nonumber \end{array}\right.\]

Ejercicio\(\PageIndex{22}\)

Antes del tiempo t = 0 minutos, un tambor está vacío. Al tiempo t = 0 minutos se enciende una manguera y el nivel del agua en el tambor comienza a subir a una velocidad constante de 2 pulgadas cada minuto. Dejar que h represente el nivel de agua (en pulgadas) en el tiempo t (en minutos). Esbozar la gráfica de h versust, etiquetar los ejes con las unidades apropiadas, luego proporcionar una definición por partes de tiene una función de t.