4.2: Valor Absoluto
( \newcommand{\kernel}{\mathrm{null}\,}\)
Ahora que tenemos los fundamentos de las funciones definidas poco a poco, estamos listos para introducir la función de valor absoluto. Primero, digamos un recordatorio trivial de lo que significa tomar el valor absoluto de un número real.
En cierto sentido, el valor absoluto de un número es una medida de su magnitud, sans (sin) su signo. Por lo tanto,
|7|=7 and |−7|=7
Aquí está la definición formal del valor absoluto de un número real.
Definición: Valor Absoluto
Para encontrar el valor absoluto de cualquier número real, primero localice el número en la línea real.
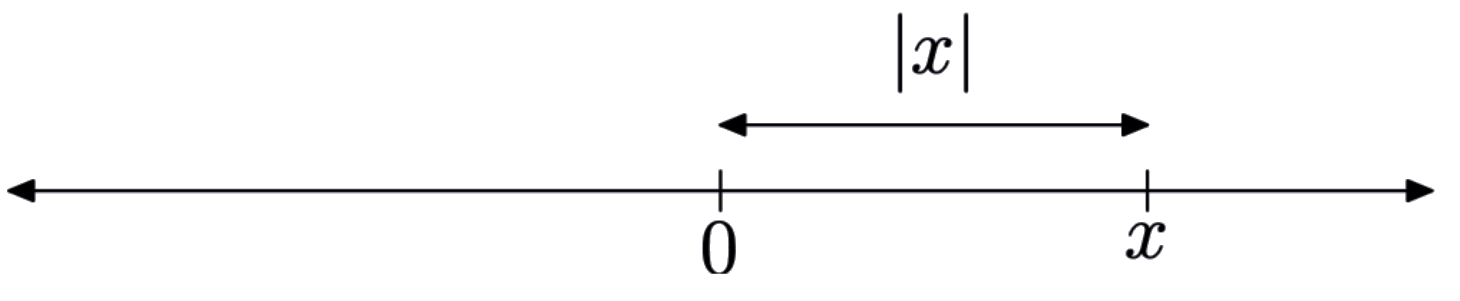
El valor absoluto del número se define como su distancia desde el origen.
Por ejemplo, para encontrar el valor absoluto de 7, localiza 7 en la línea real y luego encuentra su distancia desde el origen.
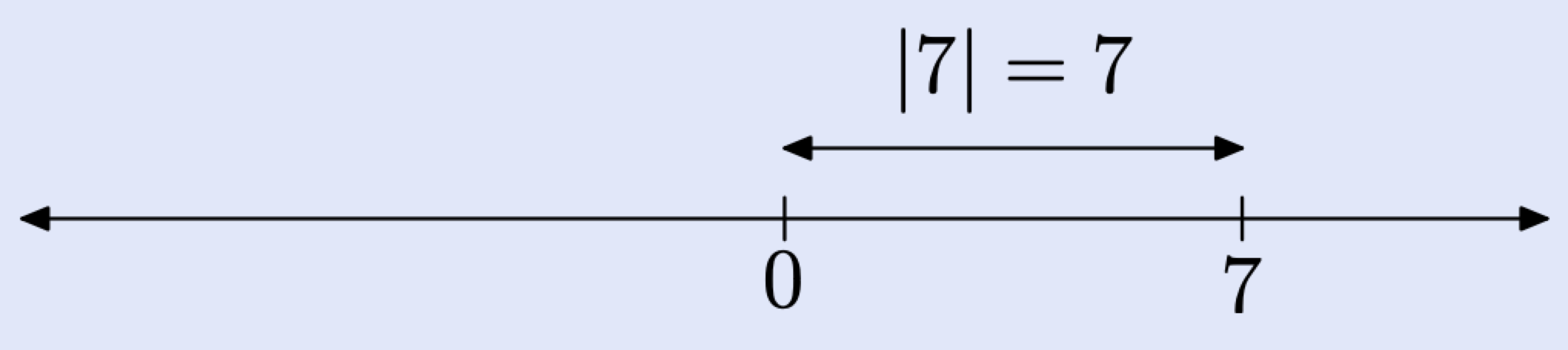
Para encontrar el valor absoluto de −7, localice −7 en la línea real y luego encuentre su distancia desde el origen.
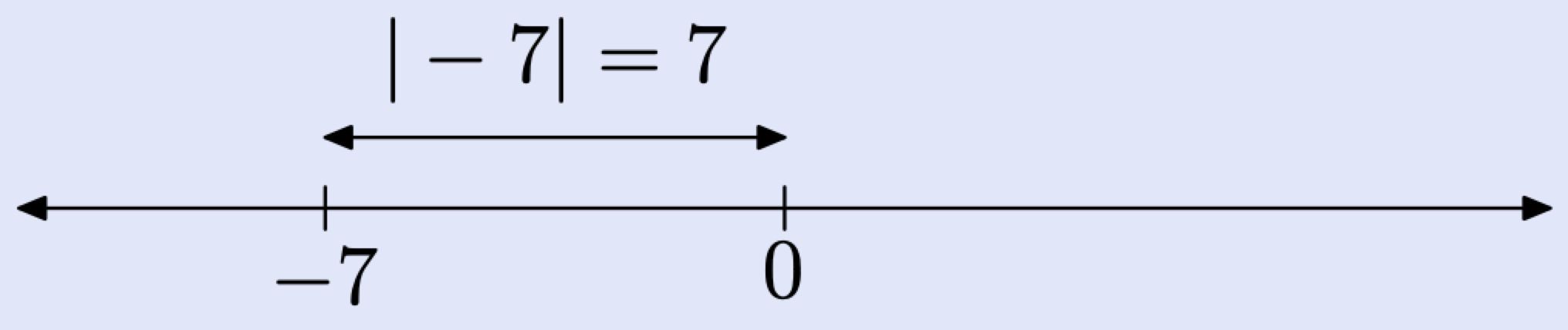
A algunos les gusta decir que tomar el valor absoluto “produce un número que siempre es positivo”. Sin embargo, esto ignora una excepción importante, es decir,
|0|=0
Así, la afirmación correcta es “el valor absoluto de cualquier número real es positivo o es cero”, es decir, el valor absoluto de un número real es “no negativo” 2 En lugar de usar la frase “no negativo”, los matemáticos prefieren la palabra “no negativo”. Cuando tomamos el valor absoluto de un número, el resultado siempre es no negativo; es decir, el resultado es positivo o cero. En símbolos,
|x|≥0 for all real numbers x
Esto tiene perfecto sentido a la luz de la Definición 2. La distancia es siempre no negativa.
Sin embargo, la discusión anterior no es de suficiente profundidad para manejar problemas más sofisticados que involucran valor absoluto.
Una definición por tramos de valor absoluto
Debido a que el valor absoluto está íntimamente relacionado con la distancia, matemáticos y científicos lo encuentran una herramienta invaluable para la medición y el análisis de errores. Sin embargo, necesitaremos una definición formulaica del valor absoluto si queremos utilizar esta herramienta de manera significativa. Necesitamos desarrollar una definición por partes de la función de valor absoluto, una que defina el valor absoluto para cualquier número real arbitrario x.
Comenzamos con algunas observaciones. Recuerde, el valor absoluto de un número es siempre no negativo (positivo o cero).
- Si un número es negativo, negar ese número lo hará positivo. | − 5| = − (−5) = 5, y de manera similar, | − 12| = − (−12) = 12. Así, si x < 0 (si x es negativo), entonces |x| = −x.
- Si x = 0, entonces |x| = 0.
- Si un número es positivo, tomar el valor absoluto de ese número no cambiará nada.
|5|=5, and similarly, |12|=12
Así, six>0 (six es positivo), entonces|x|=x.
Podemos resumir estos tres casos con una definición por partes.
|x|={−x, if x<00, if x=0x, if x>0
Es la primera línea de nuestra definición por partes (4) que suele dejar a los alumnos rascándose la cabeza. Podrían decir “pensé que el valor absoluto hace que un número sea positivo (o cero), sin embargo lo tienes|x|=−x; es decir, tienes el valor absoluto de x igual a una x negativa”. Por más que lo intenten, esto parece contradictorio. ¿Te parece así?
No obstante, no hay contradicción. Si x < 0, es decir, si x es un número negativo, entonces −x es un número positivo, y nuestra noción intuitiva de valor absoluto no es diferente a la de nuestra definición por partes (4). Por ejemplo, si x = −8, entonces −x = 8, y aunque digamos “x negativo”, en este caso −x es un número positivo.
Si esto todavía te tiene confundido, considera el simple hecho de que x y −x deben tener “signos opuestos”. Si uno es positivo, el otro es negativo, y viceversa. En consecuencia,
- si x es positivo, entonces −x es negativo, pero
- si x es negativo, entonces −x es positivo.
Resumamos lo que hemos aprendido hasta ahora.
Resumiendo la Definición en una Línea Numérica
Nos gusta usar una línea numérica para ayudar a resumir la definición del valor absoluto de x.
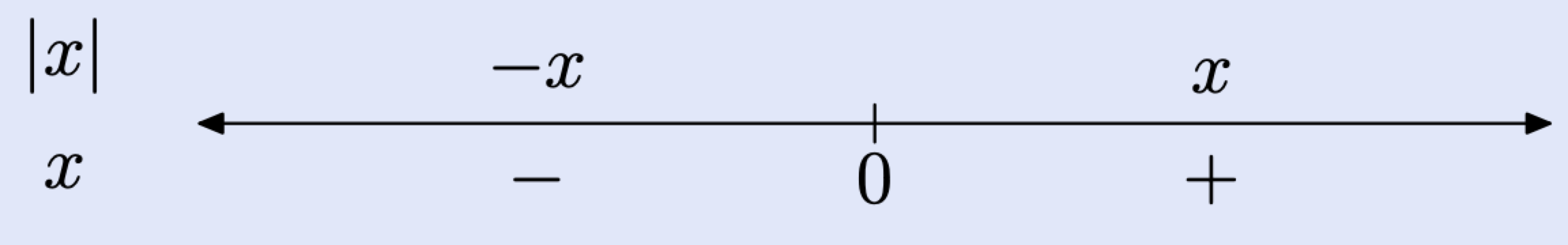
Algunas observaciones están en orden para este resumen en la línea del número.
- Primero dibujamos la línea real y luego marcamos el “valor crítico” para la expresión dentro de las barras de valor absoluto en la línea numérica. El número cero es un valor crítico para la expresión x, porque x cambia de signo a medida que se mueve de un lado de cero al otro.
- A la izquierda de cero, x es un número negativo. Esto lo indicamos con el signo menos debajo de la línea del número. A la derecha de cero, x es un número positivo, indicado con un signo más debajo de la línea numérica.
- Por encima de la recta numérica, simplificamos la expresión |x|. A la izquierda de cero, x es un número negativo (mira debajo de la línea), así que |x| = −x Observe cómo el resultado −x se coloca encima de la línea a la izquierda de cero. De igual manera, a la derecha de cero, x es un número positivo (mira debajo de la línea), así que |x| = x Observe cómo el resultado x se coloca por encima de la línea a la derecha de cero.
En la definición por partes de |x| en (4), tenga en cuenta que tenemos tres piezas distintas, una para cada caso discutido anteriormente. Sin embargo, debido a que |0| = 0, podemos incluir este caso con la pieza |x| = x, si ajustamos la condición para incluir cero.
Definición
|x|={−x, if x<0x, if x≥0
Tenga en cuenta que esta definición por partes concuerda con nuestra discusión hasta la fecha.
- En la primera línea de la ecuación (6), si x es un número negativo (es decir, six<0), entonces el valor absoluto debe cambiar x a un número positivo negando. Es decir, |x| = −x.
- En la segunda línea de la ecuación (6), si x es positivo o cero (es decir, six≥0), entonces no hay nada que hacer excepto eliminar las barras de valor absoluto. Es decir, |x| = x.
Porque |0| = −0, también podríamos incluir el caso para cero a la izquierda, definiendo el valor absoluto con
|x|={−x, if x≤0x, if x>0
No obstante, en este texto siempre incluiremos el valor crítico a la derecha, como se muestra en la Definición 5.
Construcción de definiciones por tramos
Veamos si podemos determinar definiciones por partes para otras expresiones que involucren valor absoluto.
Ejemplo4.2.1
Determine una definición por partes para |x − 2|.
Solución
Primero, establezca la expresión dentro de las barras de valor absoluto igual a cero y resuelva para x.
x−2=0x=2
Tenga en cuenta que x − 2 = 0 en x = 2. Este es el “valor crítico” para esta expresión. Dibuja una línea real y marca este valor crítico de x en la línea. Coloque la expresión x − 2 debajo de la línea en su extremo izquierdo.

A continuación, determine el signo de x − 2 para valores de x en cada lado de 2. Esto se hace fácilmente “probando” un punto a cada lado de 2 en la expresión x − 2.
- Toma x = 1, que se encuentra a la izquierda del valor crítico 2 en nuestra recta numérica. Sustituir este valor de x en la expresión x − 2, obteniendo
x−2=1−2=−1
que es negativo. De hecho, independientemente del valor x que elija a la izquierda de 2, cuando se inserta en la expresión x − 2, obtendrá un resultado negativo (debe verificar esto para otros valores de x a la izquierda de 2). Indicamos que la expresión x − 2 es negativa para los valores de x a la izquierda de 2 colocando un signo menos (−) debajo de la recta numérica a la izquierda de 2.

- A continuación, pick x = 3, que se encuentra a la derecha del valor crítico 2 en la recta numérica. Sustituir este valor de x en la expresión x − 2, obteniendo
x−2=3−2=1
lo cual es positivo. De hecho, independientemente del valor x que elija a la derecha de 2, cuando se inserta en la expresión x − 2, obtendrá un resultado positivo (debe verificar esto para otros valores de x a la derecha de 2). Indicamos que la expresión x − 2 es positiva para valores de x a la derecha de 2 colocando un signo más (+) debajo de la recta numérica a la derecha de 2 (ver la línea numérica arriba).
El siguiente paso es eliminar las barras de valor absoluto de la expresión |x−2|, dependiendo del signo de x − 2.
- A la izquierda de 2, la expresión x − 2 es negativa (anote el signo menos (−) debajo de la línea numérica), por lo que |x − 2| = − (x − 2). Es decir, tenemos que negar x − 2 para que sea positivo. Esto se indica colocando − (x − 2) por encima de la línea a la izquierda de 2.
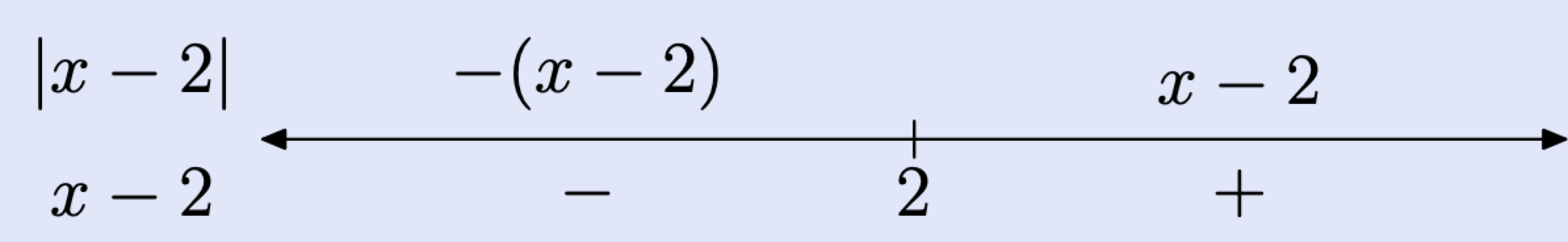
- A la derecha de 2, la expresión x − 2 es positiva (anote el signo más (+) debajo de la línea), por lo que |x − 2| = x − 2. Es decir, simplemente eliminamos las barras de valor absoluto porque la cantidad interior ya es positiva. Esto se indica colocando x − 2 encima de la línea a la derecha de 2 (ver la línea numérica anterior).
Podemos usar este último resumen de líneas numéricas para construir una definición por partes de la expresión |x − 2|.
|x−2|={−(x−2), if x<2,x−2, if x≥2={−x+2, if x<2x−2, if x≥2
Nuestra línea numérica y definición por partes coinciden: |x − 2| = − (x − 2) a la izquierda de 2 y |x − 2| = x − 2 a la derecha de 2. Además, observe cómo hemos incluido el valor crítico de 2 “a la derecha” en nuestra definición por partes.
Resumamos el método que seguimos para construir la función por partes anterior.
Construcción de una definición por tramos para el valor absoluto
Cuando se le presenta el valor absoluto de una expresión algebraica, realice los siguientes pasos para eliminar las barras de valor absoluto y construir una definición equivalente por partes.
- Tome la expresión que está dentro de las barras de valor absoluto y establezca esa expresión igual a cero. Entonces resuelve para x Este valor de x se llama “valor crítico”. (Nota: La expresión dentro de las barras de valor absoluto podría tener más de un valor crítico. No encontraremos este tipo de problemas en este texto.)
- Coloca tu valor crítico en una recta numérica.
- Coloque la expresión dentro de las barras de valor absoluto debajo de la línea numérica en el extremo izquierdo.
- Pruebe el signo de la expresión dentro de las barras de valor absoluto insertando un valor de x desde cada lado del valor crítico y marcando el resultado con un signo más (+) o menos (−) debajo de la línea numérica.
- Coloque la expresión original, la que incluye las barras de valor absoluto, por encima de la recta numérica en el extremo izquierdo.
- Use el signo de la expresión dentro de las barras de valor absoluto (indicadas por los signos más y menos debajo de la línea numérica) para eliminar las barras de valor absoluto, colocando los resultados por encima de la recta numérica a cada lado del valor crítico.
- Construya una definición por partes que imite los resultados en la recta numérica.
Apliquemos esta técnica a otro ejemplo.
Ejemplo4.2.2
Determine una definición por partes para |3 − 2x|.
Solución
Paso 1: Primero establece la expresión dentro de las barras de valor absoluto igual a cero y resuelve para x.
3−2x=0x=3/2
Tenga en cuenta que 3 − 2x = 0 en x = 3/2. Este es el “valor crítico” para esta expresión.
Pasos 2 y 3: Dibuja una recta numérica y marca este valor crítico en la línea. El siguiente paso requiere que coloquemos la expresión dentro de las barras de valor absoluto, es decir, 3 − 2x, debajo de la línea en su extremo izquierdo.

Paso 4: A continuación, determine el signo de 3 − 2x para valores de x en cada lado de 3/2. Esto se hace fácilmente “probando” un punto en cada lado de 3/2 en la expresión 3 − 2x.
- Toma x = 1, que se encuentra a la izquierda de 3/2. Sustituir este valor de x en la expresión 3 − 2x, obteniendo3−2x=3−2(1)=1 lo que es positivo. Indique este resultado colocando un signo más (+) debajo de la línea numérica a la izquierda de 3/2.

- A continuación, pick x = 2, que se encuentra a la derecha de 3/2. Sustituir este valor de x en la expresión 3 − 2x, obteniendo3−2x=3−2(2)=−1 lo que es negativo. Indique este resultado colocando un signo negativo (−) debajo de la línea a la derecha de 3/2 (ver la línea numérica anterior).
Pasos 5 y 6: Coloque la expresión original, es decir |3 − 2x|, por encima de la línea numérica en el extremo izquierdo. El siguiente paso es eliminar las barras de valor absoluto de la expresión |3 − 2x|.
- A la izquierda de 3/2, la expresión 3 − 2x es positiva (anote el signo más (+) debajo de la línea numérica), así que |3−2x| = 3−2x. Indique este resultado colocando la expresión 3 − 2x por encima de la línea numérica a la izquierda de 3/2.
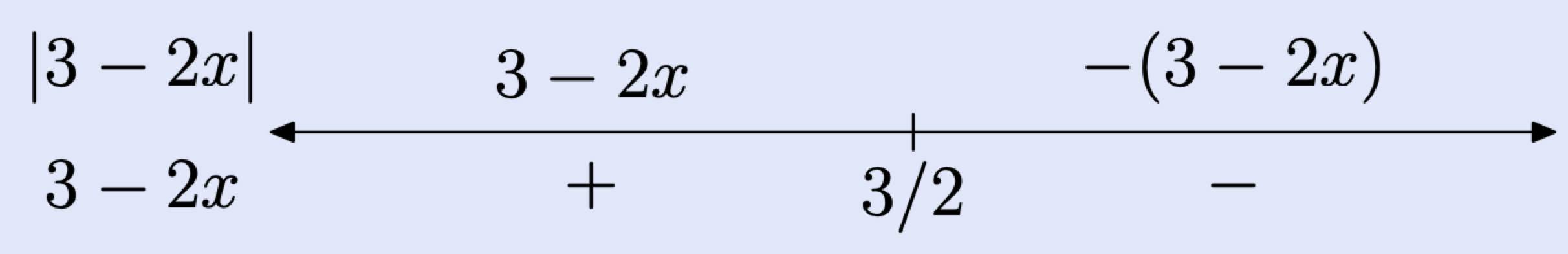
- A la derecha de 3/2, la expresión 3−2x es negativa (observe el signo menos (−) debajo de la línea numérica), así que |3−2x| = − (3−2x). Es decir, tenemos que negar 3−2x para que sea positivo. Esto se indica colocando la expresión − (3 − 2x) por encima de la línea a la derecha de 3/2 (ver la línea numérica anterior).
Paso 7: Podemos usar este último resumen de líneas numéricas para escribir una definición por partes para la expresión |3 − 2x|.
|3−2x|={3−2x, if x<3/2.−(3−2x), if x≥3/2={3−2x, if x<3/2−3+2x, if x≥3/2
Nuevamente, observe cómo hemos incluido el valor crítico de 3/2 “a la derecha”.
Dibujo de la Gráfica de una Función de Valor Absoluto
Ahora que sabemos construir una definición por partes para una expresión que contenga barras de valor absoluto, podemos usar lo que aprendimos en la sección anterior para dibujar la gráfica.
Ejemplo4.2.3
Dibuja la gráfica de la función f (x) = |3 − 2x|.
Solución
En Ejemplo4.2.2, construimos la siguiente definición por partes.
f(x)=|3−2x|={3−2x, if x<3/2−3+2x, if x≥3/2
Ahora esbozamos cada pieza de esta función.
- Si x < 3/2, entonces f (x) = 3 − 2x (ver ecuación (10)). Se trata de un rayo, comenzando en x = 3/2 y extendiéndose hacia la izquierda. A x = 3/2,
f(3/2)=3−2(3/2)=3−3=0
Así, el punto final del rayo se localiza en (3/2, 0).
A continuación, elija un valor de x que se encuentre a la izquierda de 3/2. A x = 0,
f(0)=3−2(0)=3−0=3
Así, un segundo punto en el rayo es (0, 3).
En la Figura se muestra una tabla que contiene los dos puntos evaluados y un boceto del rayo acompañante4.2.1. Debido a que f (x) = 3 − 2x solo si x es estrictamente menor que 3/2, el punto en (3/2, 0) está sin rellenar.
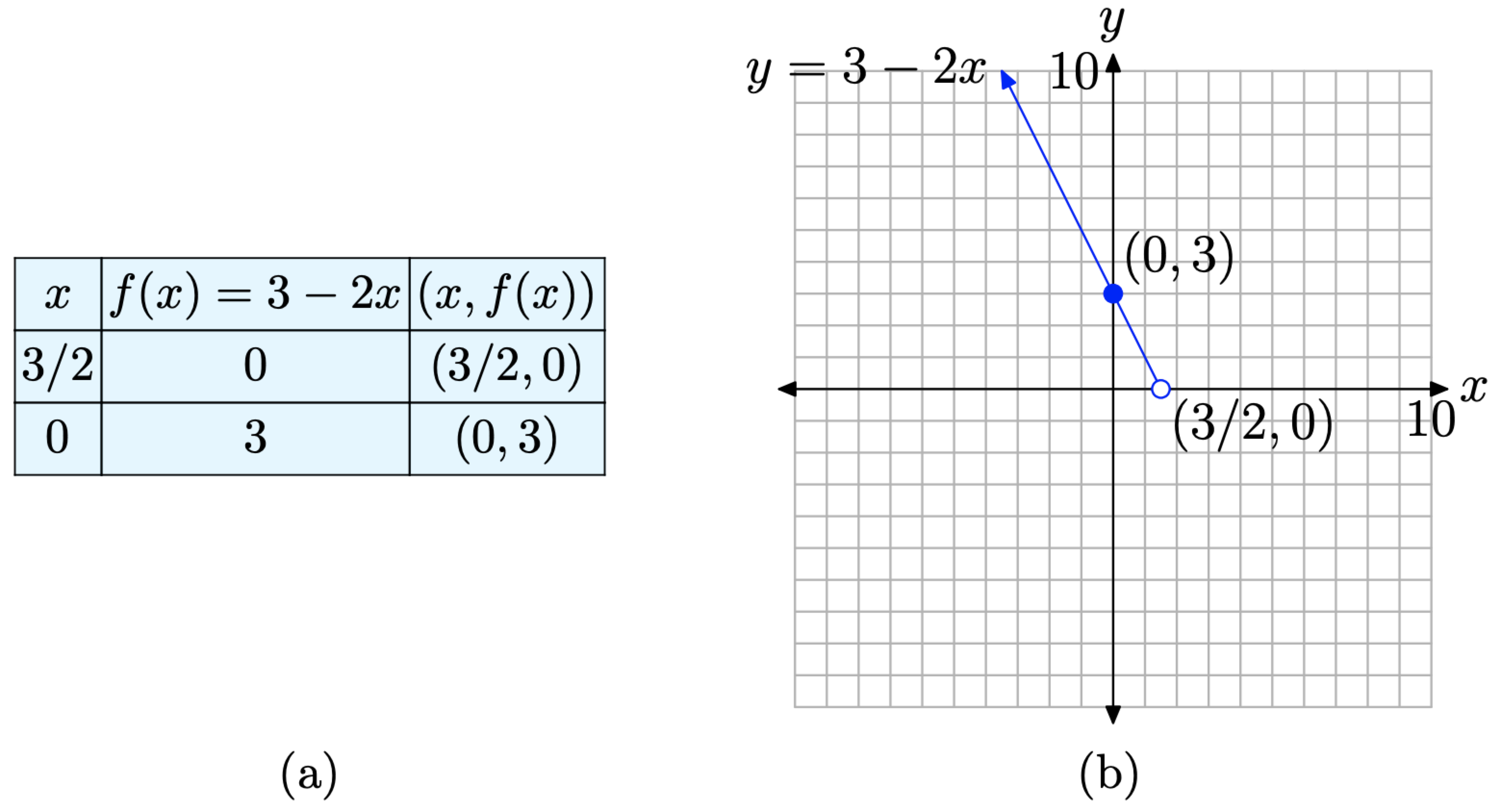
- Si x ≥ 3/2, entonces f (x) = −3 + 2x (ver ecuación (10)). Se trata de un rayo, comenzando en x = 3/2 y extendiéndose hacia la derecha. A x = 3/2,f(3/2)=−3+2(3/2)=−3+3=0
Así, el punto final del rayo se localiza en (3/2, 0).
A continuación, elija un valor de x que se encuentre a la derecha de 3/2. A x = 3,f(3)=−3+2(3)=−3+6=3
Así, un segundo punto en el rayo es (3, 3). En la Figura se muestra una tabla que contiene los dos puntos evaluados y un boceto del rayo acompañante4.2.2. Debido a que f (x) = −3 + 2x para todos los valores de x que son mayores o iguales a 3/2, el punto en (3/2, 0) se rellena en esta gráfica.
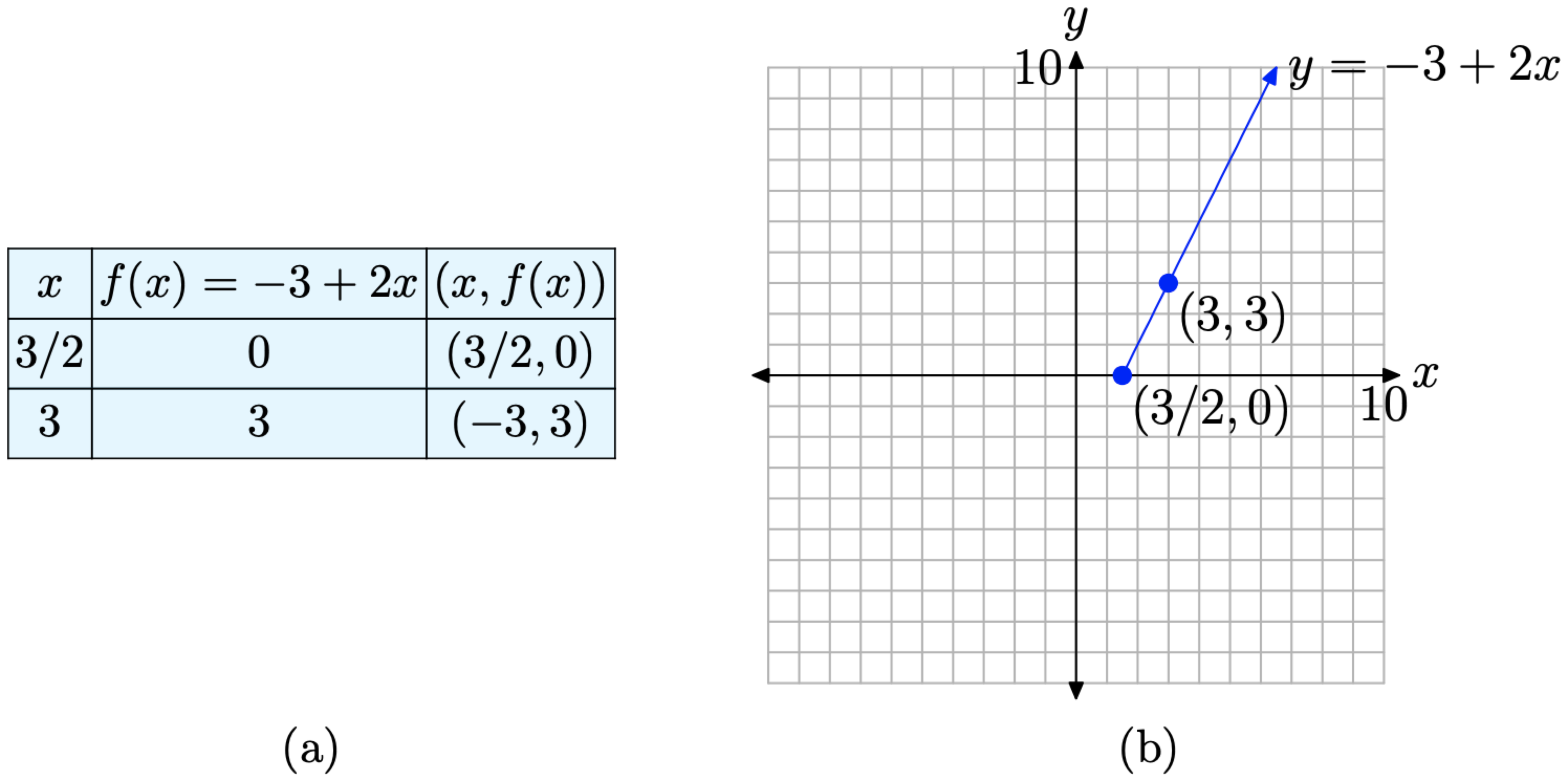
- Para bosquejar la gráfica de f (x) = |3 − 2x|, solo necesitamos combinar las dos piezas de Figuras4.2.1 y4.2.2. El resultado se muestra en la Figura4.2.3.
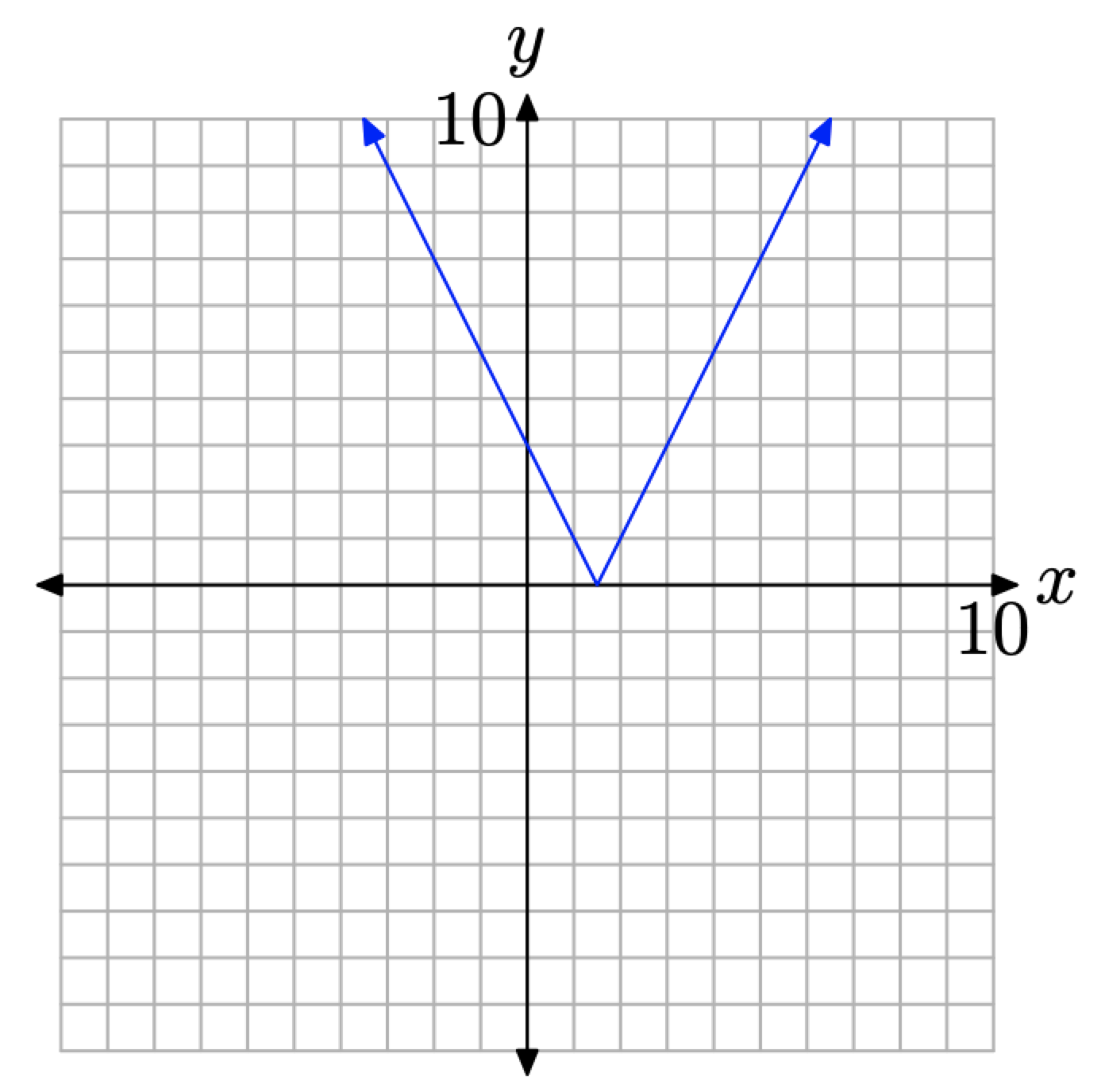
Anote la “forma de V” de la gráfica. Nos referiremos al punto en la punta de la “V” como el vértice de la función de valor absoluto.
En la Figura4.2.3, la ecuación de la rama izquierda de la “V” es y = 3 − 2x. Un enfoque alternativo para dibujar esta rama es señalar que su gráfica está contenida en la gráfica de la línea completa y = 3 − 2x, que tiene pendiente −2 e intercepción y en (0, 3). Así, se podría dibujar la línea completa usando la pendiente y la intercepción y, luego, borrar esa parte de la línea que se encuentra a la derecha de x = 3/2. Una estrategia similar funcionaría para la rama derecha de y = |3 − 2x|.
Uso de transformaciones
Consideremos nuevamente la definición básica del valor absoluto de x.
f(x)=|x|={−x, if x<0x, if x≥0
Algunas observaciones básicas son:
- Si x < 0, entonces f (x) = −x Este rayo comienza en el origen y se extiende hacia la izquierda con pendiente −1. Su gráfica se representa en la Figura4.2.4 (a).
- Six≥0, entonces f (x) = x Este rayo comienza en el origen y se extiende hacia la derecha con pendiente 1. Su gráfica se representa en la Figura4.2.4 (b).
- Combinamos las gráficas en las Figuras4.2.4 (a) y4.2.4 (b) para producir la gráfica de f (x) = |x| en la Figura4.2.4 (c).
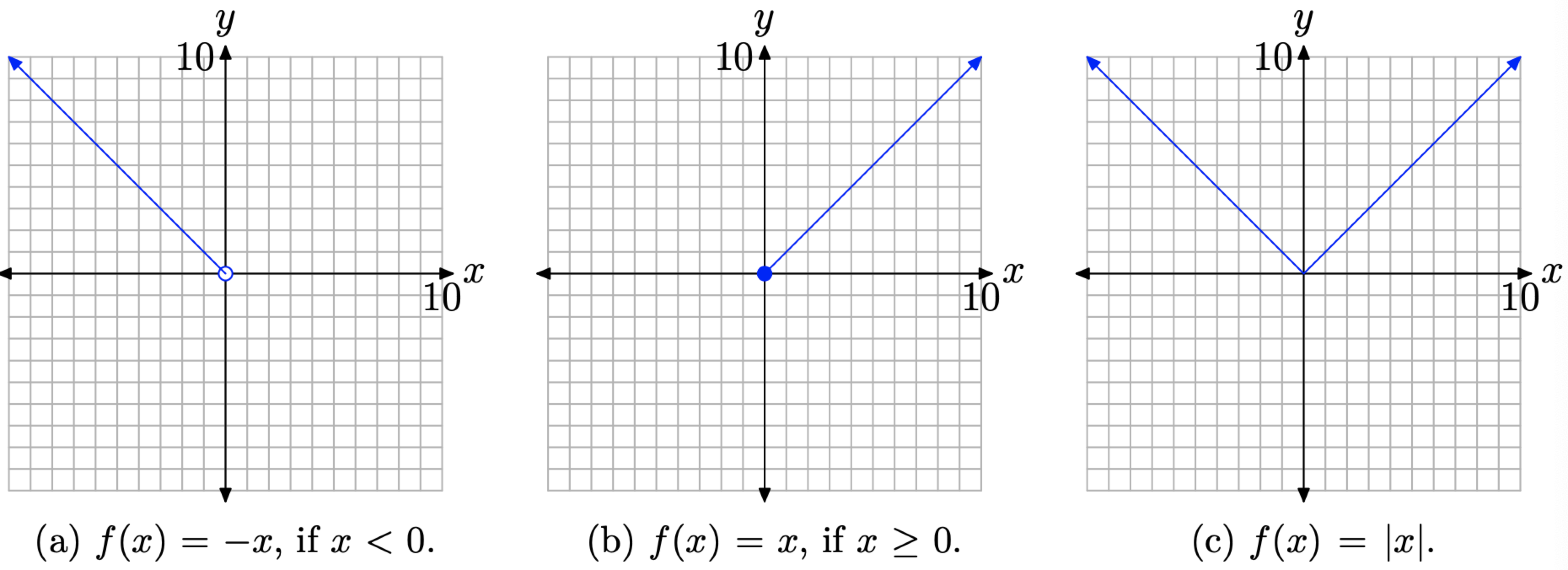
Debes comprometer la gráfica de f (x) = |x| a la memoria. Cosas a tener en cuenta:
- La gráfica de f (x) = |x| es “en forma de V.”
- El vértice de la gráfica está en el punto (0, 0).
- La rama izquierda tiene la ecuación y = −x y pendiente −1.
- La rama derecha tiene la ecuación y = x y pendiente 1.
- Cada rama de la gráfica de f (x) = |x| forma un ángulo perfecto de 45◦ con el eje x.
Ahora que sabemos dibujar la gráfica de f (x) = |x|, podemos usar las transformaciones que aprendimos en el Capítulo 2 (secciones 5 y 6) para bosquejar una serie de gráficas simples que involucran valor absoluto.
Ejemplo4.2.4
Esbozar la gráfica de f (x) = |x − 3|.
Solución
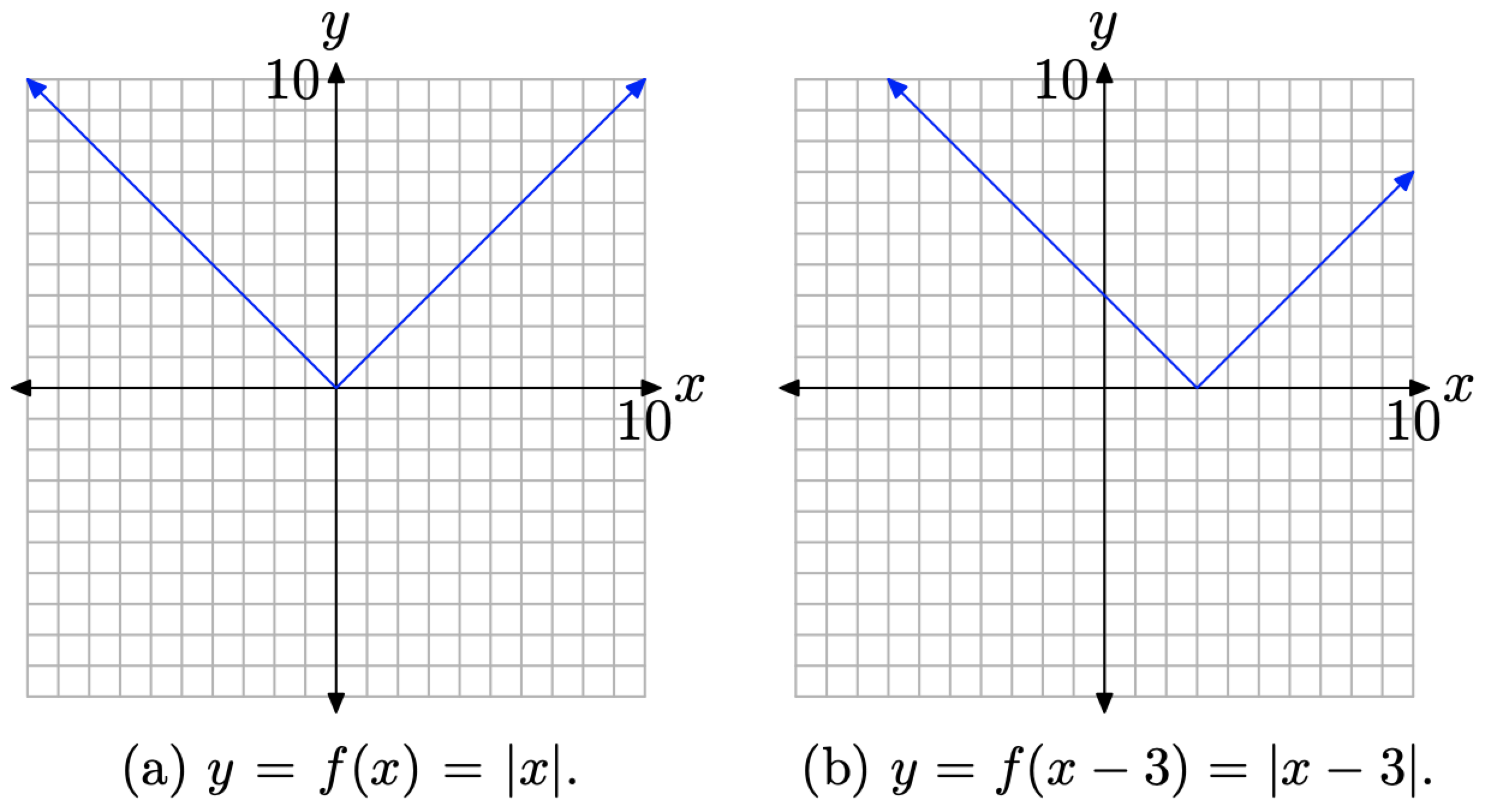
Primero, bosquejar la gráfica de y = f (x) = |x|, como se muestra en la Figura4.2.5 (a). Tenga en cuenta que si f (x) = |x|, entonces
y=f(x−3)=|x−3|
Para bosquejar la gráfica de y = f (x − 3) = |x − 3|, desplace la gráfica de y = f (x) = |x| tres unidades hacia la derecha, produciendo el resultado mostrado en la Figura4.2.5 (b).
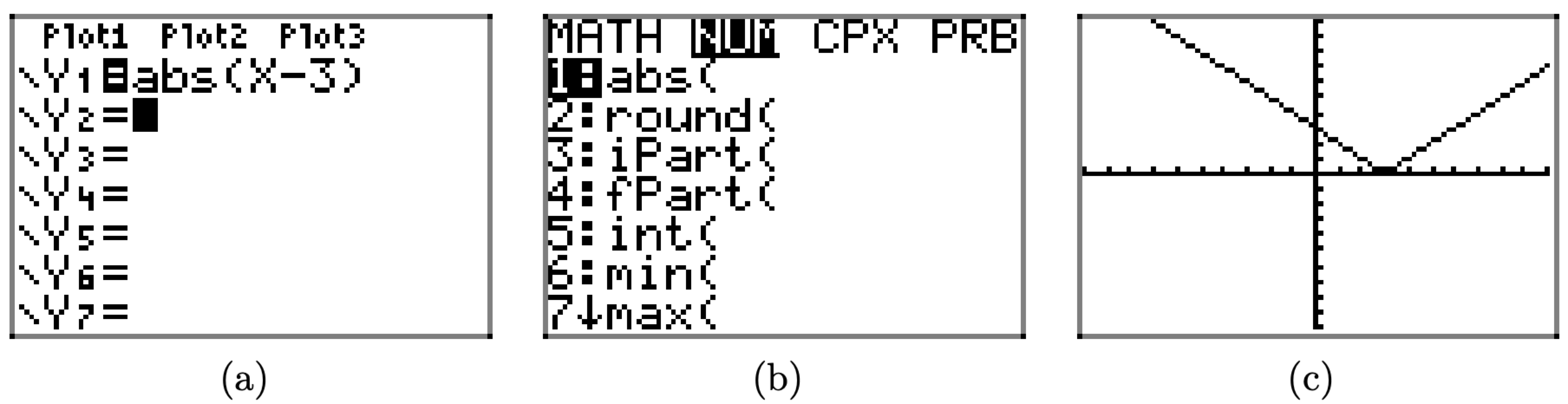
Podemos verificar este resultado usando la calculadora gráfica. Cargue la función f (x) = |x − 3| en Y1 en el menú Y= en su calculadora gráfica como se muestra en la Figura4.2.6 (a). Presione el botón MATH, flecha derecha hacia el menú NUM, luego seleccione 1:abs ((ver Figura4.2.6 (b)) para ingresar el valor absoluto en Y1. Presione el botón ZOOM y, a continuación, seleccione 6:ZStandard para producir la imagen que se muestra en la Figura4.2.6 (c).
Veamos otro ejemplo sencillo.
Ejemplo4.2.5
Esbozar la gráfica de f (x) = |x| − 4.
Solución
Primero, bosquejar la gráfica de y = f (x) = |x|, como se muestra en la Figura4.2.7 (a). Tenga en cuenta que si f (x) = |x|, entoncesy=f(x)−4=|x|−4
Para bosquejar la gráfica de y = f (x) − 4 = |x| − 4, desplaza la gráfica de y = f (x) = |x| hacia abajo 4 unidades, produciendo el resultado mostrado en la Figura4.2.5 (b).
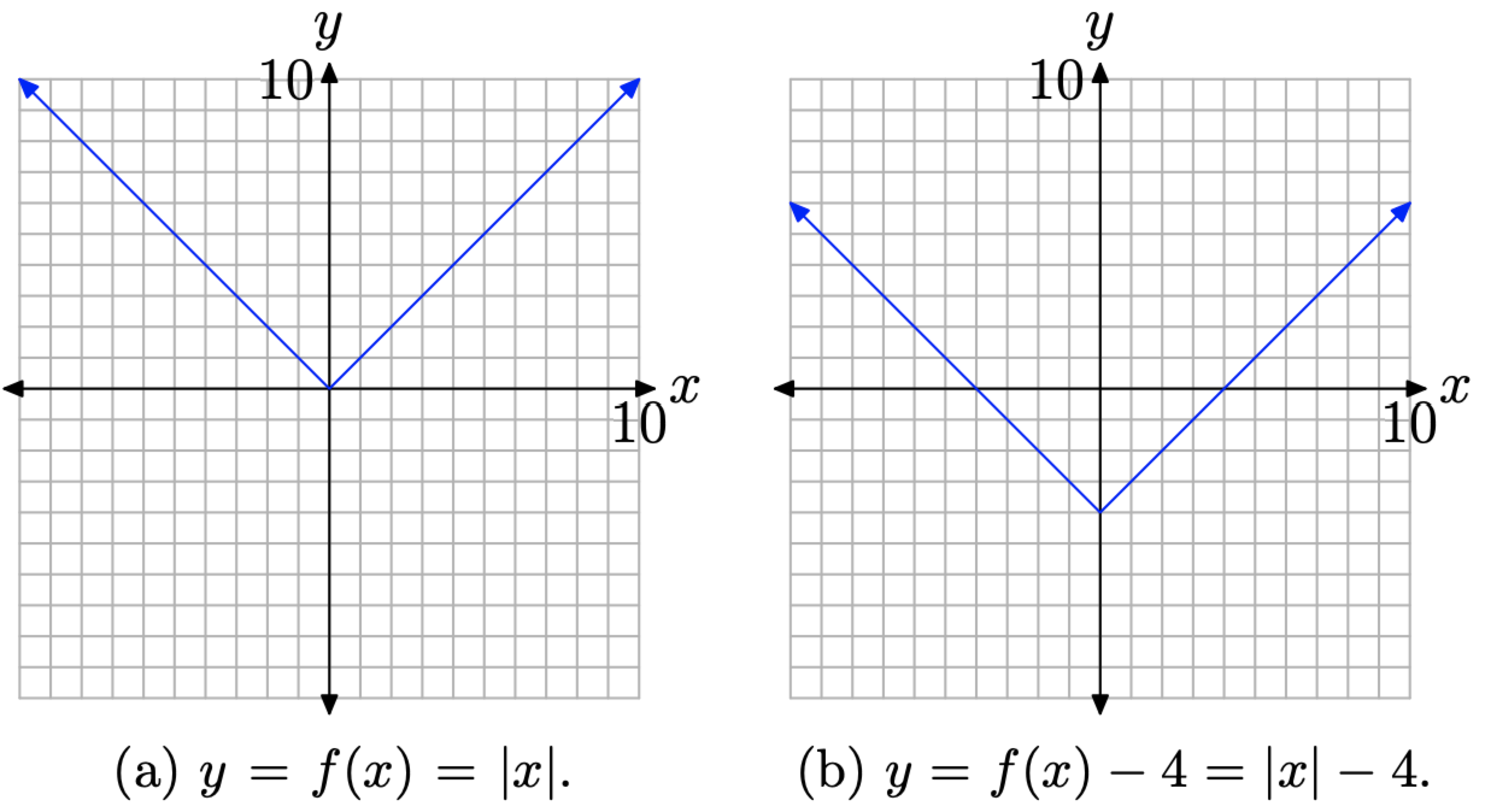
Veamos un último ejemplo.
Ejemplo4.2.6
Esboza la gráfica de f (x) = −|x| + 5. Indicar el dominio y el rango de esta función.
Solución
- Primero, bosquejar la gráfica de y = f (x) = |x|, como se muestra en la Figura4.2.8 (a).
- A continuación, dibuje la gráfica de y = −f (x) = −|x|, que es un reflejo de la gráfica de y = f (x) = |x| a través del eje x y se representa en la Figura4.2.8 (b).
- Por último, vamos a querer esbozar la gráfica de y = −f (x) + 5 = −|x| + 5. Para ello, desplazamos la gráfica de y = −f (x) = −|x| en la Figura4.2.8 (b) hacia arriba 5 unidades para producir el resultado en la Figura4.2.8 (c).
Para encontrar el dominio de f (x) = −|x| + 5, proyecte todos los puntos de la gráfica sobre el eje x, como se muestra en la Figura4.2.9 (a). Así, el dominio de f es(−∞,∞). Para encontrar el rango, proyecte todos los puntos de la gráfica sobre el eje y, como se muestra en la Figura4.2.9 (b). Así, el rango es(−∞,5].
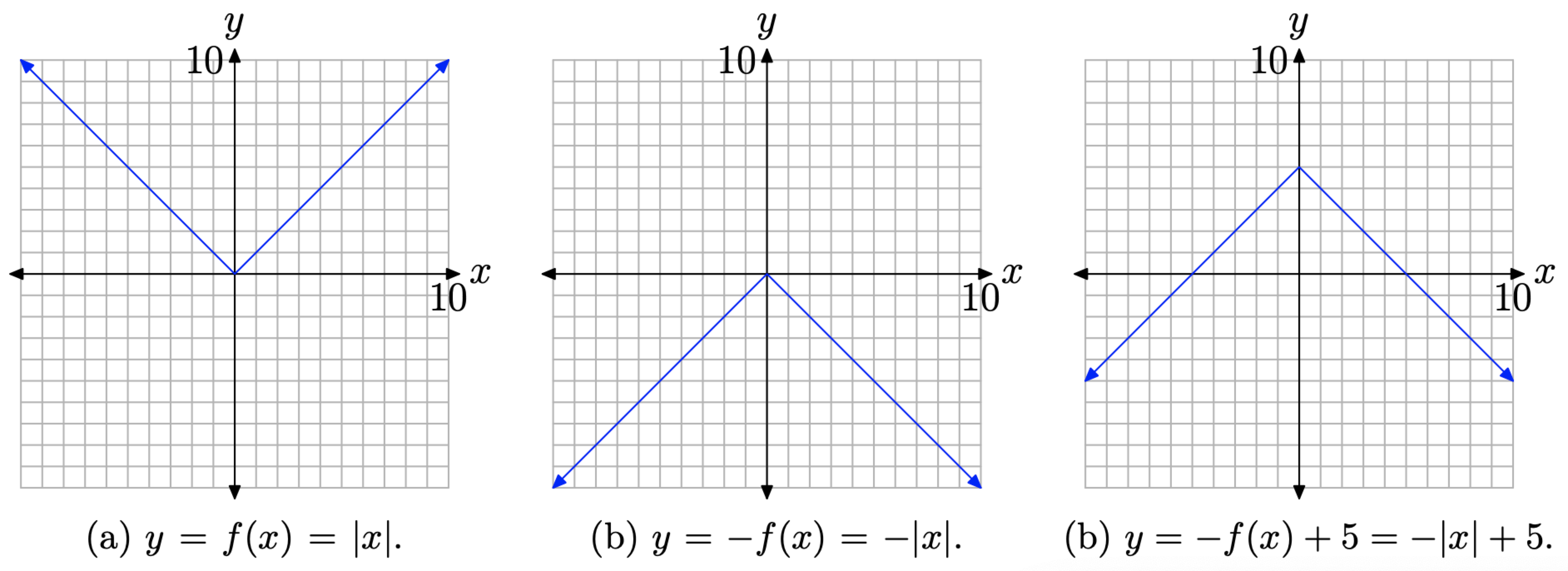
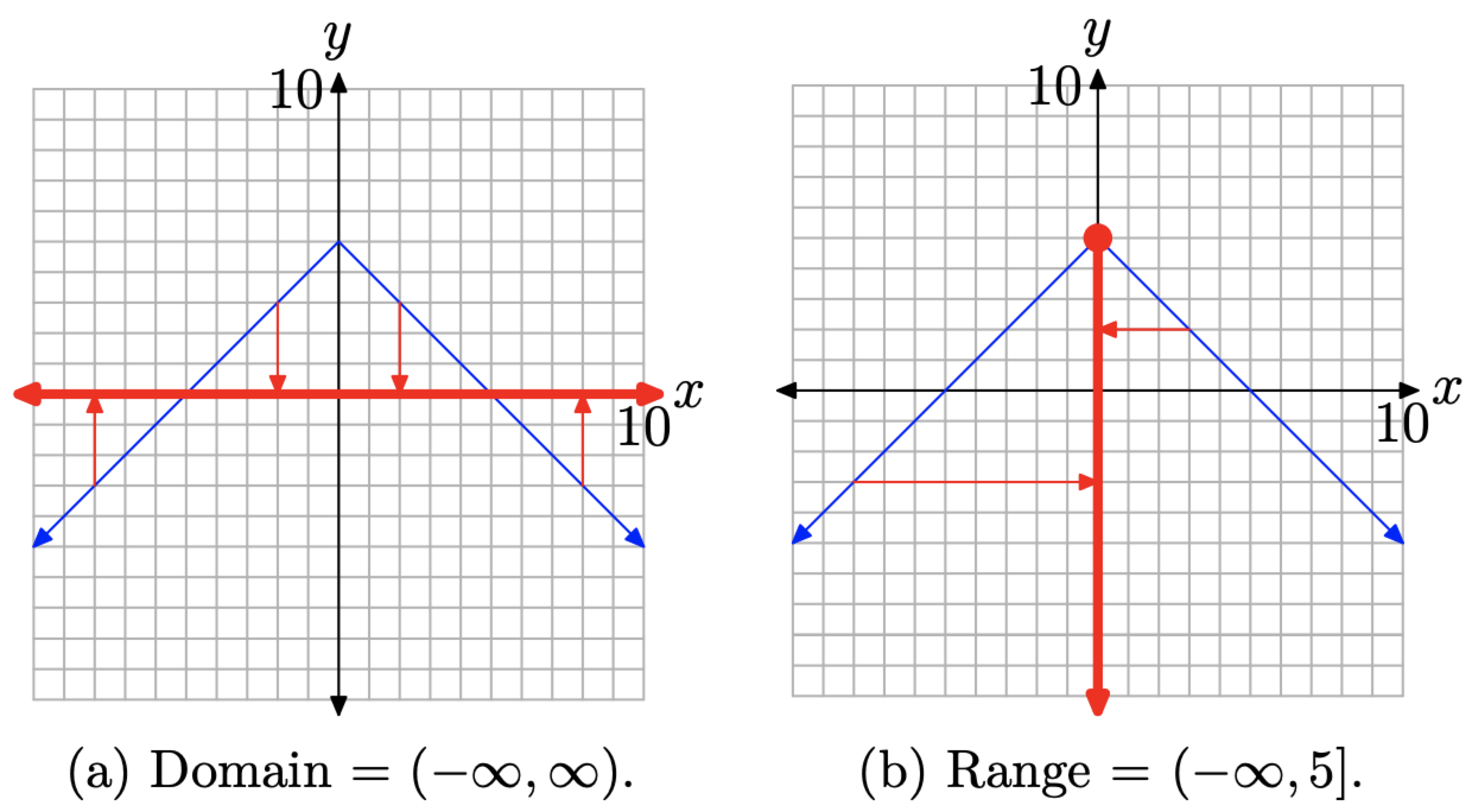
Figura4.2.9. Proyectar sobre los ejes para encontrar el dominio y el rango
Ejercicio
Para cada una de las funciones en los Ejercicios 1 - 8, como en los Ejemplos 7 y 8 en la narrativa, marcar el “valor crítico” en una recta numérica, luego marcar el signo de la expresión dentro de las barras de valor absoluto debajo de la línea numérica. Por encima de la línea numérica, elimine las barras de valor absoluto de acuerdo con el signo de la expresión que marcó debajo de la línea numérica. Una vez que su resumen de línea numérica haya terminado, cree una definición por partes para la función de valor absoluto dada.
Ejercicio4.2.1
f (x) = |x+1|
- Responder
-
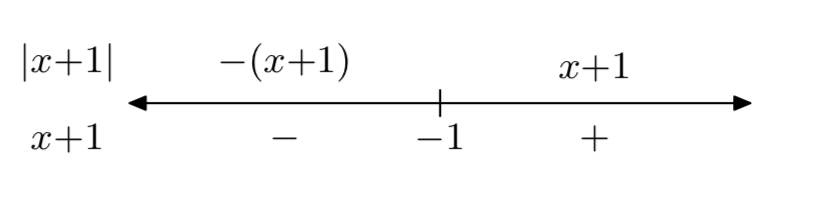
f(x)={−x−1, if x<−1x+1, if x≥−1
Ejercicio4.2.2
f (x) = |x−4|
Ejercicio4.2.3
g (x) = |4−5x|
- Responder
-
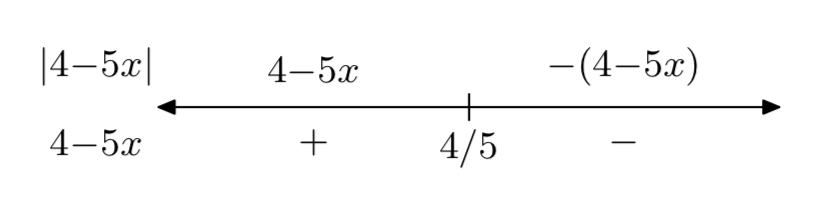
g(x)={4−5x, if x<45−4+5x, if x≥45
Ejercicio4.2.4
g (x) = |3−2x|
Ejercicio4.2.5
h (x) = |−x−5|
- Responder
-
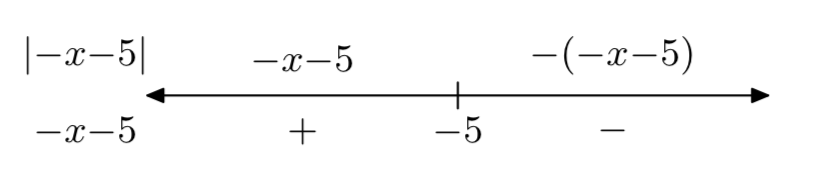
h(x)={−x−5, if x<−5x+5, if x≥−5
Ejercicio4.2.6
h (x) = |−x−3|
Ejercicio4.2.7
f (x) = x+|x|
- Responder
-
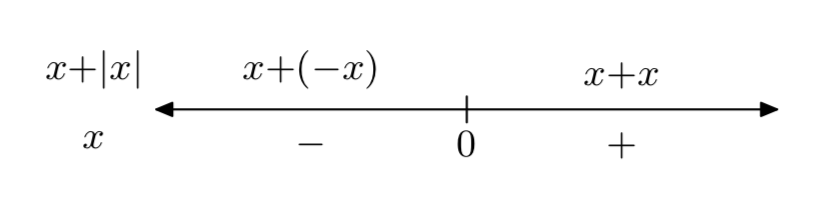
f(x)={0, if x<02x, if x≥0
Ejercicio4.2.8
f(x)=|x|x
Para cada una de las funciones de los Ejercicios 9 - 16, realizar cada una de las siguientes tareas.
- Crear una definición por partes para la función dada, utilizando la técnica de los Ejercicios 1 - 8 y los Ejemplos 7 y 8 en la narrativa.
- Siguiendo el ejemplo del Ejemplo 9 en la narrativa, use su definición por partes para bosquejar el gráfico de la función dada en una hoja de papel cuadriculado. Por favor, coloque cada ejercicio en su propio sistema de coordenadas.
Ejercicio4.2.9
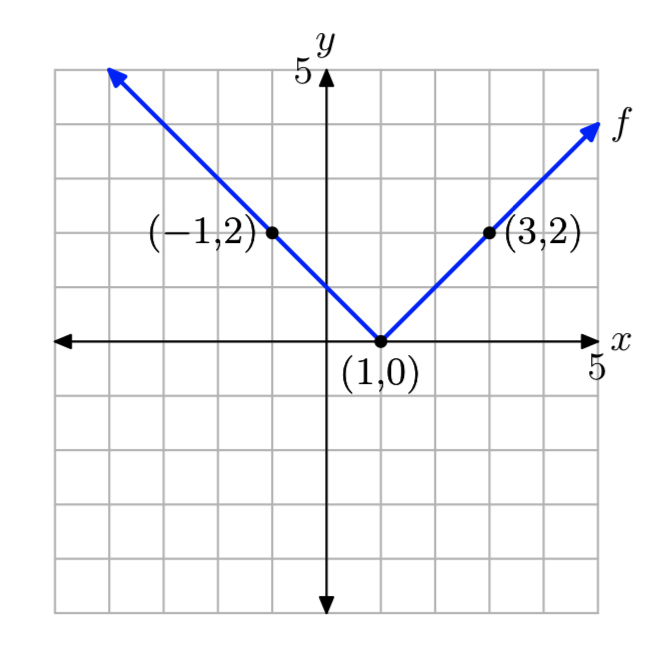
f (x) = |x−1|
- Responder
-
f(x)={−x+1, if x<1x−1, if x≥1
Ejercicio4.2.10
f (x) = |x+2|
Ejercicio4.2.11
g (x) = |2x−1|
- Responder
-
g(x)={−2x+1, if x<122x−1, if x≥12
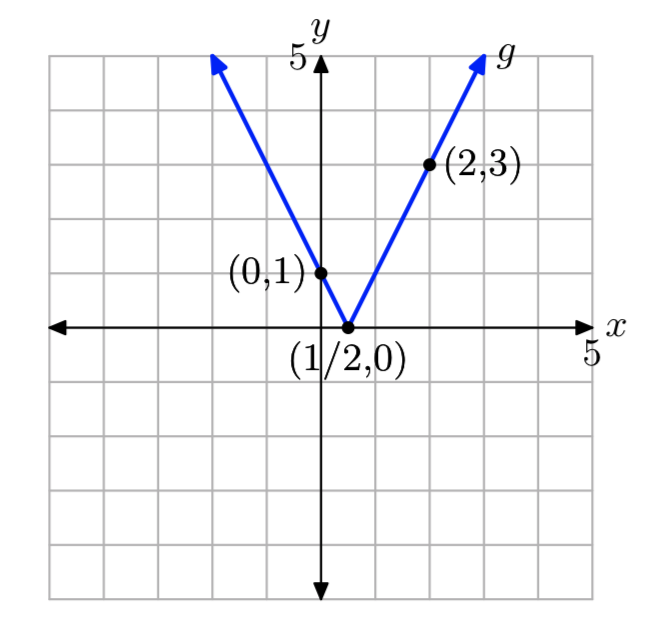
Ejercicio4.2.12
g (x) = |5−2x|
Ejercicio4.2.13
h (x) = |1−3x|
- Responder
-
h(x)={1−3x, if x<13−1+3x, if x≥13
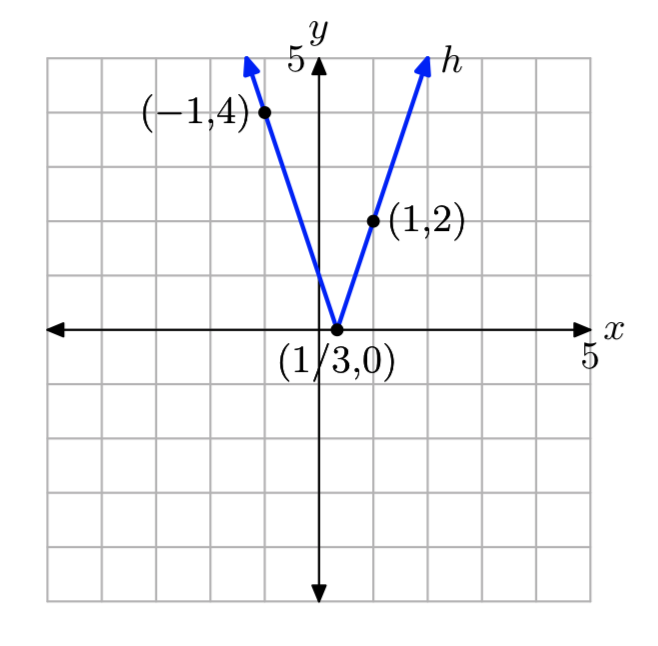
Ejercicio4.2.14
h (x) = |2x+1|
Ejercicio4.2.15
f (x) = x−|x|
- Responder
-
f(x)={2x, if x<00, if x≥0
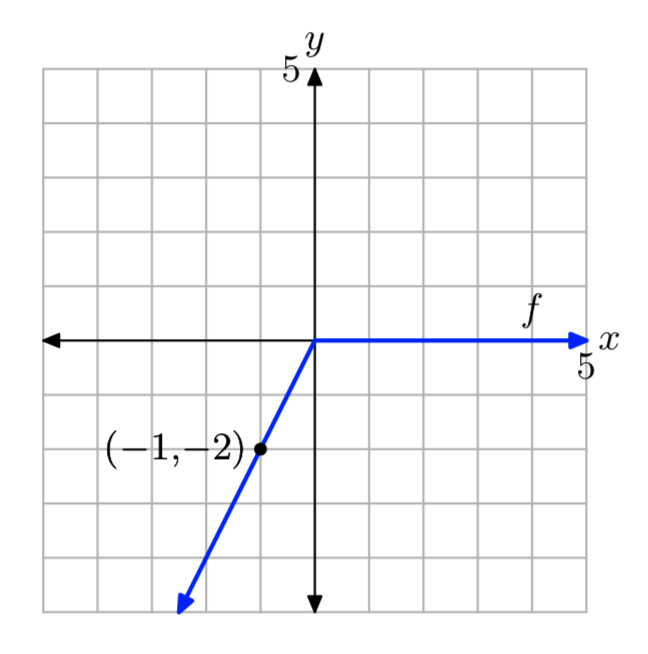
Ejercicio4.2.16
f (x) = x+|x−1|
Ejercicio4.2.17
Utilice una calculadora gráfica para dibujar las gráficas de y = |x|, y = 2|x|, y = 3|x| e y = 4|x| en la misma ventana de visualización. En sus propias palabras, explique lo que aprendió en este ejercicio.
- Responder
-
Multiplicando por un factor de a > 1, como en y = a|x|, estira la gráfica de y = |x| verticalmente por un factor de a.Cuanto mayor sea el valor de a, más se estira verticalmente.
Ejercicio4.2.18
Use una calculadora gráfica para dibujar las gráficas de y = |x|, y = (1/2) |x|, y = (1/3) |x| e y = (1/4) |x| en la misma ventana de visualización. En sus propias palabras, explique lo que aprendió en este ejercicio.
Ejercicio4.2.19
Utilice una calculadora gráfica para dibujar las gráficas de y = |x|, y = |x−2|, y =|x−4| e y = |x−6| en la misma ventana de visualización. En sus propias palabras, explique lo que aprendió en este ejercicio.
- Responder
-
Al restar un valor positivo de a, como en y = |x−a|, desplaza la gráfica a unidades hacia la derecha.
Ejercicio4.2.20
Utilice una calculadora gráfica para dibujar las gráficas de y = |x|, y = |x+2|, y = |x+4|, e y = |x+6| en la misma ventana de visualización. En sus propias palabras, explique lo que aprendió en este ejercicio.
En Ejercicios 21 - 36, realice cada una de las siguientes tareas. Siéntase libre de verificar su trabajo con su calculadora gráfica, pero debería poder hacer todo el trabajo a mano.
- Configure un sistema de coordenadas en una hoja de papel cuadriculado. Etiquetar y escalar cada eje. Cree una gráfica precisa de la función y = |x| en su sistema de coordenadas y etiquete esta gráfica con su ecuación.
- Utilice la técnica de los Ejemplos 12,13 y 14 en la narrativa para ayudar a seleccionar las transformaciones geométricas apropiadas para transformar la ecuación y = |x| en la forma de la función dada en el ejercicio. En el mismo sistema de coordenadas, usa un lápiz o bolígrafo de diferentes colores para dibujar la gráfica de la función resultante de tu transformación aplicada. Etiquete la gráfica resultante con su ecuación.
- Utilice la notación de intervalos para describir el dominio y el rango de la función dada.
Ejercicio4.2.21
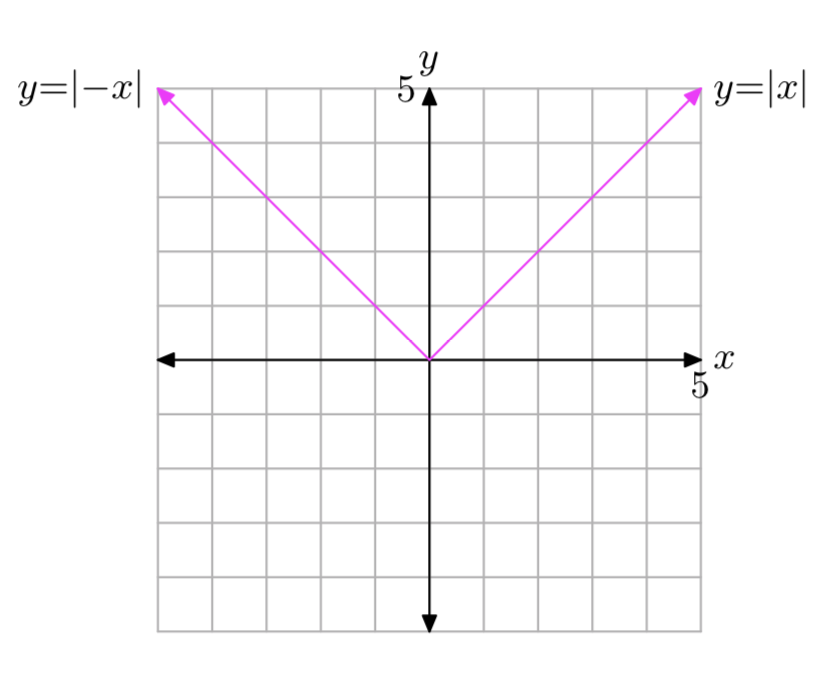
f (x) = |−x|
- Responder
-
Las gráficas de y = |x| e y = |−x| coinciden. El dominio es(−∞,∞) y el rango es[0,∞).
Ejercicio4.2.22
f (x) = −|x|
Ejercicio4.2.23
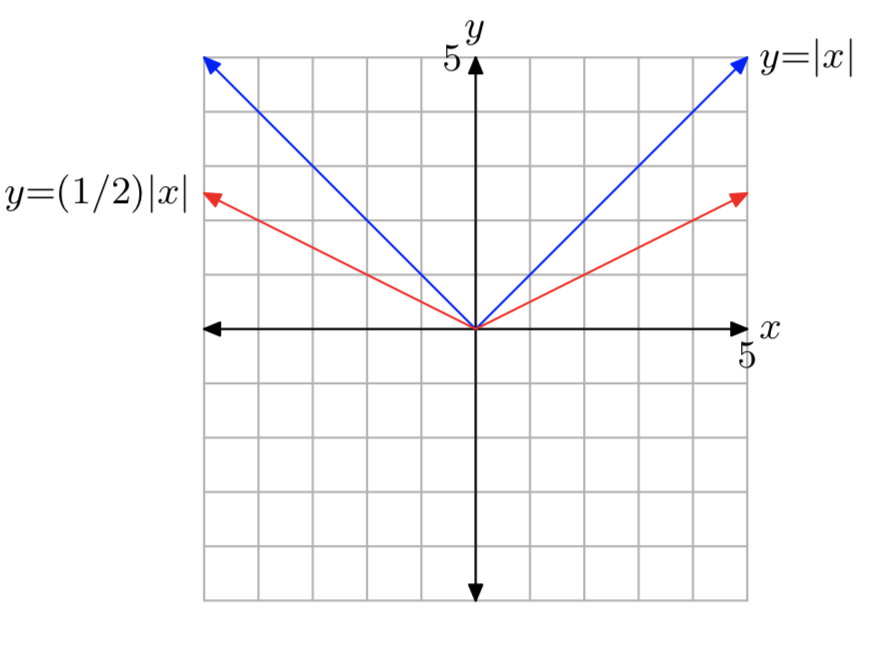
f(x)=12|x|
- Responder
-
El dominio es(−∞,∞) y el rango es[0,∞).
Ejercicio4.2.24
f (x) = −2|x|
Ejercicio4.2.25
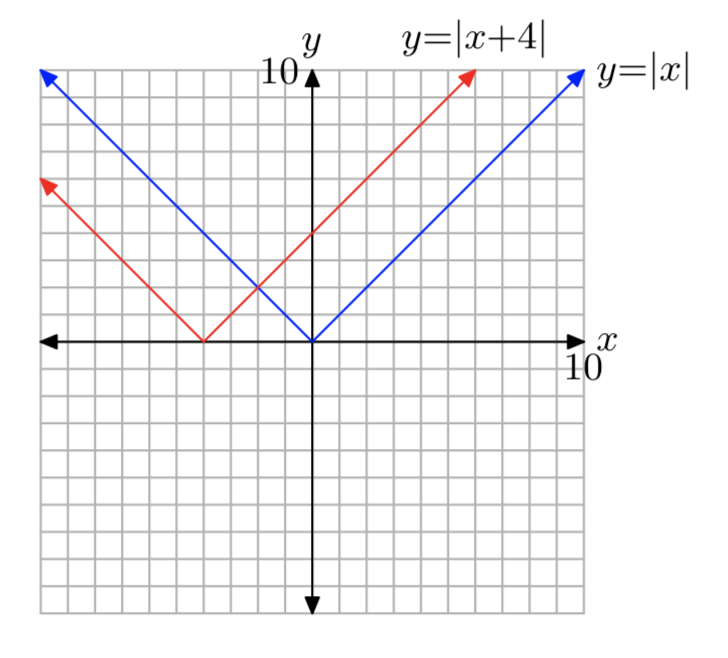
f (x) = |x+4|
- Responder
-
El dominio es(−∞,∞) y el rango es[0,∞).
Ejercicio4.2.26
f (x) = |x−2|
Ejercicio4.2.27
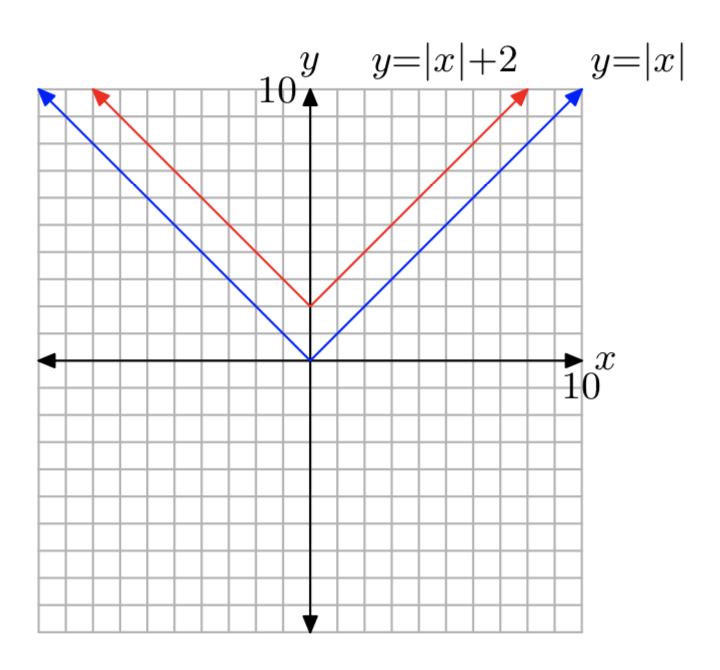
f (x) = |x|+2
- Responder
-
El dominio es(−∞,∞) y el rango es[2,∞).
Ejercicio4.2.28
f (x) = |x|−3
Ejercicio4.2.29
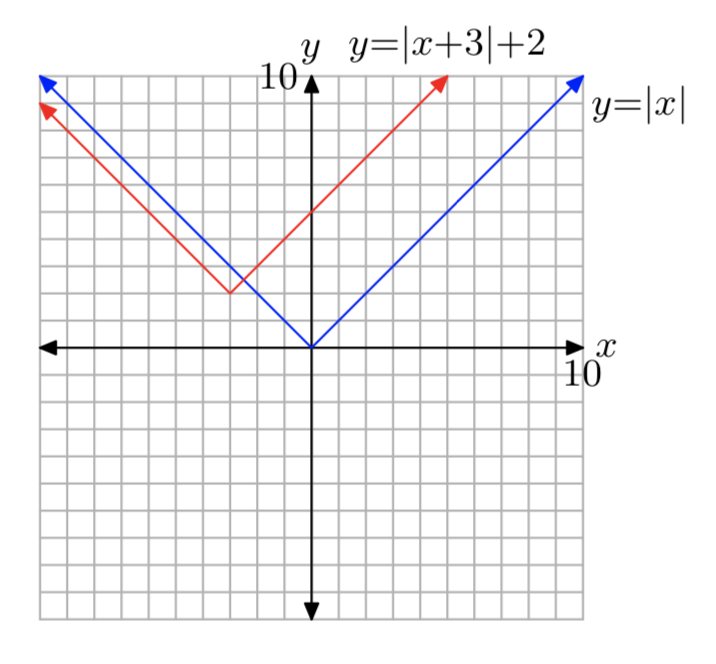
f (x) = |x+3|+2
- Responder
-
El dominio es(−∞,∞) y el rango es[2,∞).
Ejercicio4.2.30
f (x) = |x−3|−4
Ejercicio4.2.31
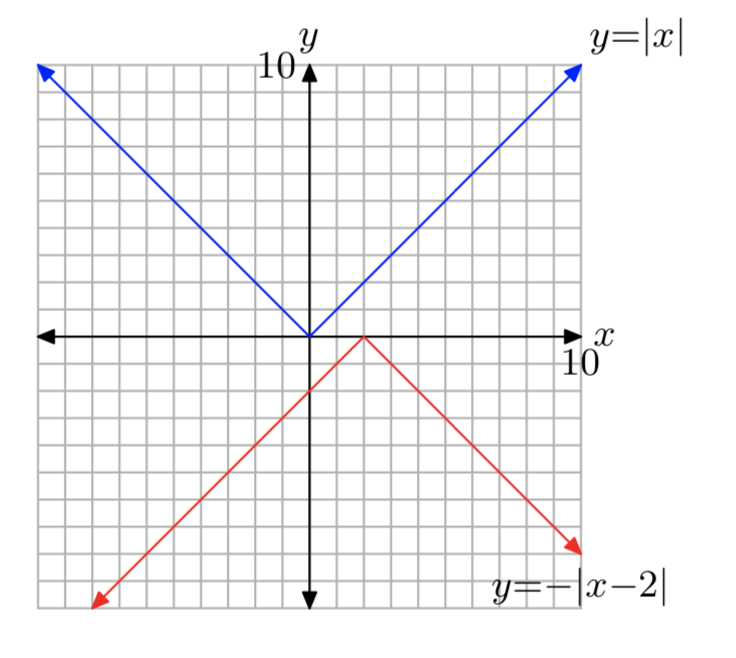
f (x) = −|x−2|
- Responder
-
El dominio es(−∞,∞) y el rango es(−∞,0].
Ejercicio4.2.32
f (x) = −|x|−2
Ejercicio4.2.33
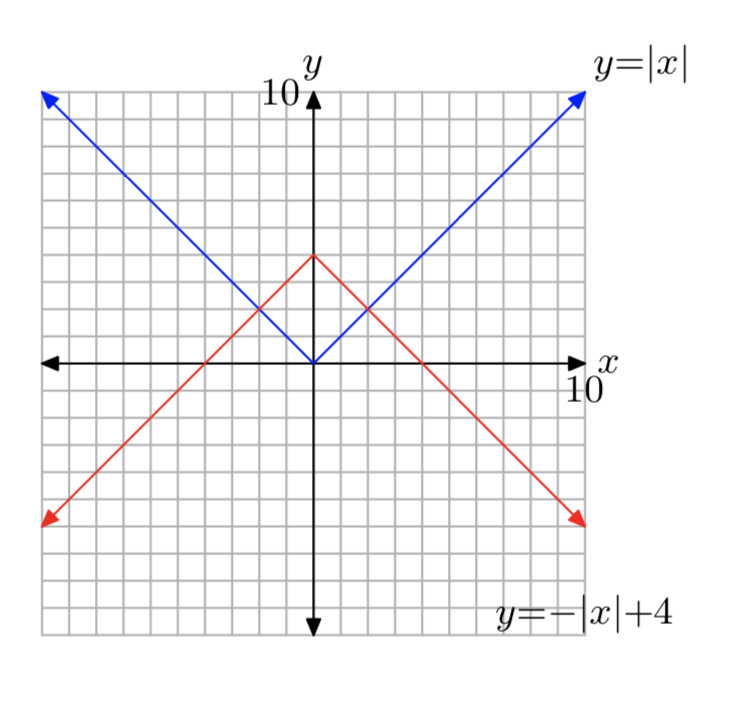
f (x) = −|x|+4
- Responder
-
El dominio es(−∞,∞) y el rango es(−∞,4].
Ejercicio4.2.34
f (x) = −|x+4|
Ejercicio4.2.35
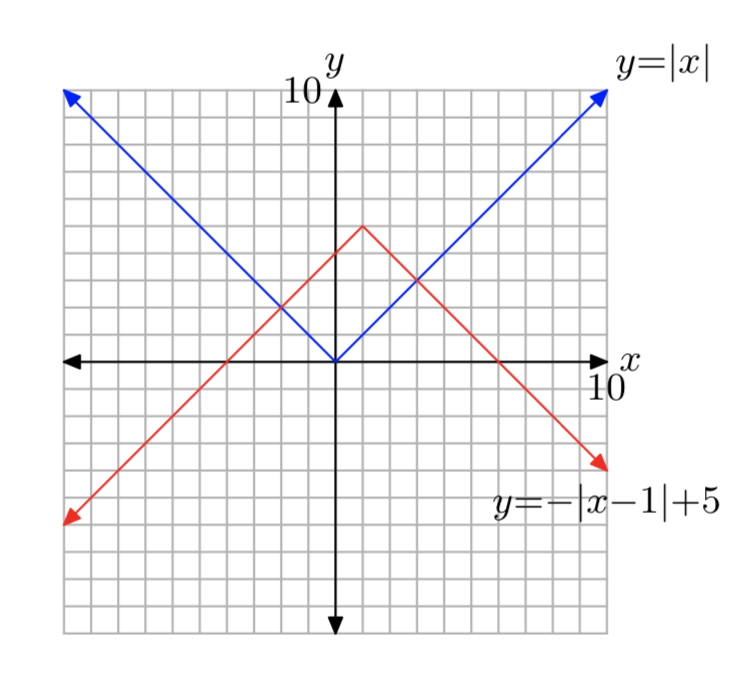
f (x) = −|x−1|+5
- Responder
-
El dominio es(−∞,∞) y el rango es(−∞,5].
Ejercicio4.2.36
f (x) = −|x+5|+2


