8.7: Crecimiento y Decaimiento Exponencial

Modelos de Crecimiento Exponencial

Recordando las investigaciones de la Sección 8.3, comenzamos desarrollando una fórmula para el interés compuesto discreto. Esto condujo a otra fórmula para el interés compuesto continuo,

\(P(t) = P_{0}e^{rt}\), (1)

donde\(P_{0}\) es el monto inicial (principal) y r es la tasa de interés anual en forma decimal. Si el dinero en una cuenta bancaria crece a una tasa anual r (vía pago de intereses), y si el crecimiento se agrega continuamente a la cuenta (es decir, el interés se compone continuamente), entonces el saldo en la cuenta en el momento t años es P (t), como lo da la fórmula (1).

Pero podemos usar exactamente el mismo análisis para cantidades distintas al dinero. Si P (t) representa la cantidad de alguna cantidad en el tiempo t años, y si P (t) crece a una tasa anual r con el crecimiento continuamente agregado en, entonces podemos concluir de la misma manera que P (t) debe tener la forma

\(P(t) = P_{0}e^{rt}\), (2)

donde\(P_{0}\) es la cantidad inicial en el tiempo t = 0, es decir P (0).

Un ejemplo clásico es el crecimiento desinhibido de la población. Si una población P (t) de cierta especie se coloca en un buen ambiente, con abundantes nutrientes y espacio para crecer, entonces crecerá de acuerdo a la fórmula (2). Por ejemplo, el tamaño de un cultivo bacteriano en una placa de Petri seguirá muy de cerca esta fórmula si se le proporcionan condiciones de vida óptimas. Muchas otras especies de animales y plantas también exhibirán este comportamiento si se colocan en un ambiente en el que no tienen depredadores. Por ejemplo, cuando los británicos importaron conejos a Australia a finales del siglo XVIII para la caza, la población de conejos explotó porque las condiciones eran buenas para vivir y reproducirse, y no había depredadores naturales de los conejos.

Crecimiento exponencial

Si una función P (t) crece continuamente a una velocidad r > 0, entonces P (t) tiene la forma

\(P(t) = P_{0}e^{rt}\), (3)

donde\(P_{0}\) está la cantidad inicial P (0). En este caso, se dice que la cantidad P (t) exhibe crecimiento exponencial, y r es la tasa de crecimiento.

Observaciones 4.

1. Si una cantidad física (como población) crece según la fórmula (3), decimos que la cantidad es modelada por la función de crecimiento exponencial P (t).
2. Algunos pueden argumentar que el crecimiento poblacional de conejos, o incluso bacterias, no es realmente continuo. Después de todo, los conejos nacen uno a la vez, por lo que la población en realidad crece en trozos discretos. Esto es ciertamente cierto, pero si la población es grande, entonces el crecimiento parecerá ser continuo. Por ejemplo, consideremos la población mundial de humanos. Hay tanta gente en el mundo que hay muchos nuevos nacimientos y muertes cada segundo. Así, la diferencia de tiempo entre cada cambio de 1 unidad en la población es apenas una pequeña fracción de segundo, y en consecuencia el crecimiento discreto actuará prácticamente igual que el crecimiento continuo. (Esto es análogo a los resultados casi idénticos para la composición continua y la composición diaria discreta que encontramos en la Sección 8.3; componer cada segundo o milisegundo estaría aún más cerca).
3. Asimismo, el uso de la fórmula de crecimiento exponencial continuo (3) para modelar cantidades discretas a veces dará como resultado respuestas fraccionarias. En este caso, los resultados deberán ser redondeados para que tengan sentido. Por ejemplo, una respuesta de 224.57 conejos no es realmente posible, por lo que la respuesta debe redondearse a 225.
4. En la fórmula (3), si el tiempo se mide en años (como lo hemos hecho hasta ahora en este capítulo), entonces r es la tasa de crecimiento anual. Sin embargo, el tiempo se puede medir en cualquier unidad conveniente. Se aplica la misma fórmula, salvo que la tasa de crecimiento r se da en términos de las unidades de tiempo particulares utilizadas. Por ejemplo, si el tiempo t se mide en horas, entonces r es la tasa de crecimiento por hora.

   En la Sección 8.2, mostramos que una función de la forma bt con b > 1 es una exponencial

función de crecimiento. De igual manera, si A > 0, entonces la función exponencial más general\(Ab^t\) también exhibe crecimiento exponencial, ya que la gráfica de\(Ab^t\) es solo una escala vertical de la gráfica de\(b^t\). Sin embargo, la función de crecimiento exponencial en la fórmula (3) parece ser diferente. Mostraremos a continuación que la función de hecho se\(P_{0}e^{rt}\) puede escribir en la forma\(Ab^t\) con b > 1.

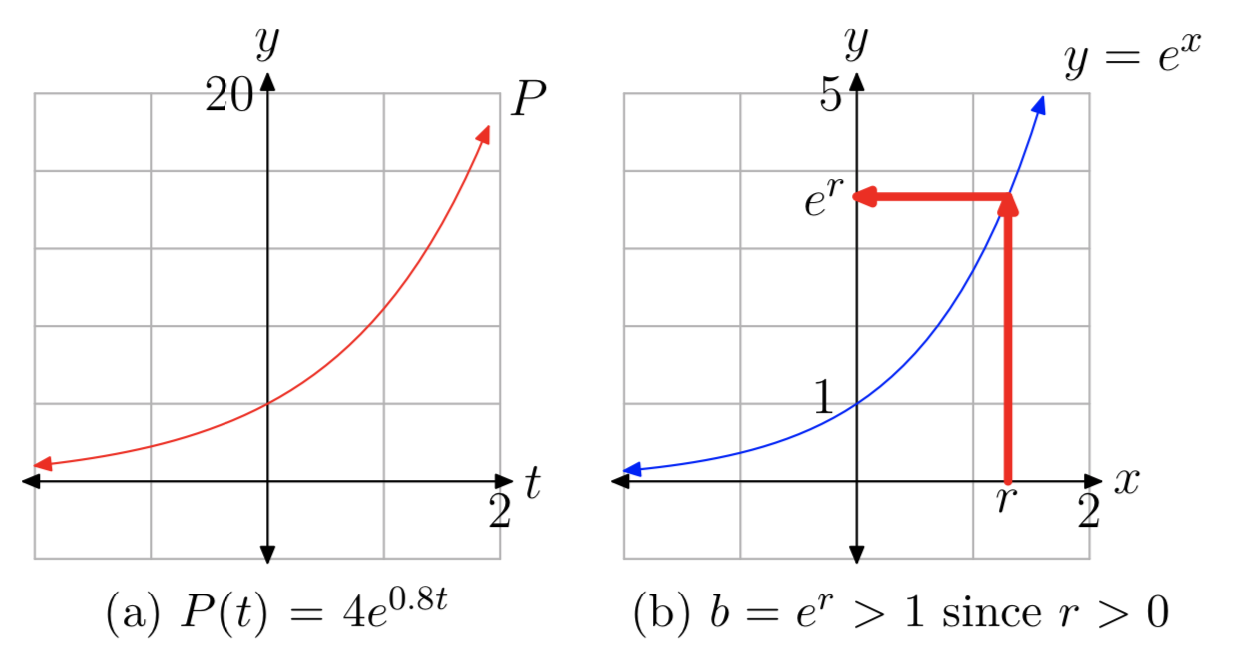
Veamos primero un ejemplo específico. Supongamos\(P(t) = 4e^{0.8t}\). Usando las Leyes de los Exponentes, podemos reescribir P (t) como

\(P(t) = 4e^{0.8t} = 4(e^{0.8})^t\). (5)

Ya que\(e^{0.8} \approx 2.22554\), de ello se deduce que

\(P(t) ≈ 4(2.22554)^t\).

Debido a que la base\(\approx 2.22554\) es mayor que 1, esto demuestra que P (t) es una función de crecimiento exponencial, como se ve en la Figura 1 (a)).

Ahora supongamos que P (t) es cualquier función de la forma\(P_{0}e^{rt}\) con r > 0. Como en (5) anterior, podemos usar las Leyes de los Exponentes para reescribir P (t) como

\(P(t) = P_{0}e^{rt} = P_{0}(e^{r})^t = P_{0}b^t\)con\(b = e^r\).

Para probar que b > 1, considere la gráfica de que\(y = e^x\) se muestra en la Figura 1 (b). Recordemos que\(e \approx 2.718\), así e > 1, y por lo tanto\(y = e^x\) es en sí misma una curva de crecimiento exponencial. Además, la intercepción y es (0,1) ya que\(e^0 = 1\). De ello se deduce que\(b = e^r > 1\) desde r > 0 (ver Figura 1 (b)).

Por lo tanto, las funciones de la forma\(P(t) = P_{0}e^{rt}\) con r > 0 son funciones de crecimiento exponencial.

Figura 1

Aplicaciones de Crecimiento Exponencial

Ahora examinaremos el papel de las funciones de crecimiento exponencial en algunas aplicaciones del mundo real. En los siguientes ejemplos, supongamos que la población está modelada por una función de crecimiento exponencial como en la fórmula (3).

Ejemplo\(\PageIndex{6}\)

Supongamos que la población de un determinado país crece a una tasa anual del 2%. Si la población actual es de 3 millones, ¿cuál será la población en 10 años?

Este es un problema de valor futuro. Si medimos la población en millones y el tiempo en años, entonces\(P(t) = P_{0}e^{rt}\) con\(P_{0} = 3\) y r = 0.02. Insertando estos valores particulares en la fórmula (3), obtenemos

\(P(t) = 3e^{0.02t}\).

La población en 10 años es\(P(10) = 3e^{(0.02)(10)} \approx 3.664208\) de millones.

Ejemplo\(\PageIndex{7}\)

En el mismo país que en el Ejemplo 6, ¿cuánto tiempo tardará la población en llegar a los 5 millones?

Como antes,

\(P(t) = 3e^{0.02t}\).

Ahora queremos saber cuándo el valor futuro P (t) de la población en algún momento t será igual a 5 millones. Por lo tanto, necesitamos resolver la ecuación P (t) = 5 para el tiempo t, lo que lleva a la ecuación exponencial

\(5 = 3e^{0.02t}\).

Utilizando el procedimiento para resolver ecuaciones exponenciales que se presentó en la Sección8.6.

\(5 = 3e^{0.02t}\).

\(\rightarrow \frac{5}{3} = e^{0.02t}\)aislar el exponencial

\(\rightarrow ln(\frac{5}{3}) = ln(e^{0.02t})\)aplicar la función de registro natural

\(\rightarrow ln(\frac{5}{3}) = 0.02t\)desde\(ln(e^x) = x\)

\(\rightarrow \frac{ln(\frac{5}{3})}{0.02} = t\)dividir

\(\rightarrow t \approx 25.54128\)

De esta manera, tardarían alrededor de 25.54 años para que la población llegara a los 5 millones.

La población de bacterias se mide típicamente en peso, como en los dos ejemplos siguientes.

Ejemplo\(\PageIndex{8}\)

Supongamos que el tamaño de un cultivo bacteriano viene dado por la función

\(P(t) = 100e^{0.15t}\),

donde el tamaño P (t) se mide en gramos y el tiempo t se mide en horas. ¿Cuánto tiempo tardará en que la cultura duplique su tamaño?

El tamaño inicial es\(P_{0} = 100\) grams, so we want to know when the future value P (t) en algún momento t será igual a 200. Por lo tanto, necesitamos resolver la ecuación P (t) = 200 para el tiempo t, lo que lleva a la ecuación exponencial

\(200 = 100e^{0.15t}\).

Utilizando el mismo procedimiento que en el último ejemplo,

\(200 = 100e^{0.15t}\)

\(\rightarrow 2 = e^{0.15t}\)aislar el exponencial

\(\rightarrow ln(2) = ln(e^{0.15t})\)aplicar la función de registro natural

\(\rightarrow ln(2) = 0.15t\)desde\(ln(e^x) = x\)

\(\rightarrow \frac{ln(2)}{0.15} = t\)división

\(\rightarrow t \approx 4.620981\).

Así, tardarían alrededor de 4.62 horas para que el tamaño se duplicara.

El último ejemplo merece un comentario adicional. Supongamos que habíamos empezado con 1000 gramos en vez de 100. Entonces para duplicar su tamaño requeriría un valor futuro de 2000 gramos. Por lo tanto, en este caso, tendríamos que resolver la ecuación

\(2000 = 1000e^{0.15t}\).

Pero el primer paso es aislar lo exponencial dividiendo ambos lados por 1000 para conseguir

\(2 = e^{0.15t}\),

y esto es lo mismo que la segunda línea de la solución en el último ejemplo, por lo que la respuesta será la misma. De igual manera, repetir este argumento para cualquier monto inicial conducirá a la misma segunda línea, y por lo tanto a la misma respuesta. Así, el tiempo de duplicación depende únicamente de r, no de la cantidad inicial\(P_{0}\).

Modelos de decaimiento exponencial

Hemos observado que si una cantidad aumenta continuamente a una tasa r, entonces es modelada por una función de la forma\(P(t) = P_{0}e^{rt}\). Pero, ¿y si una cantidad disminuye en su lugar? Aunque aquí no presentaremos los detalles, el análisis se puede realizar de la misma manera que la derivación de la fórmula de composición continua en la Sección 8.3. La única diferencia es que la tasa de crecimiento r en las fórmulas debe ser reemplazada por −r ya que la cantidad es decreciente. La conclusión es que la cantidad es modelada por una función de la forma\(P(t) = P_{0}e^{−rt}\) en lugar de\(P_{0}e^{rt}\).

Decaimiento exponencial

Si una función P (t) disminuye continuamente a una velocidad r > 0, entonces P (t) tiene la forma

\(P(t) = P_{0}e^{−rt}\), (9)

donde\(P_{0}\) está la cantidad inicial P (0). En este caso, se dice que la cantidad P (t) exhibe decaimiento exponencial, y r es la tasa de decaimiento.

En la Sección 8.2, mostramos que una función de la forma bt con b < 1 es una función de decaimiento exponencial. Asimismo, si A > 0, entonces la función exponencial más general\(Ab^t\) también exhibe decaimiento exponencial, ya que la gráfica de\(Ab^t\) es solo una escala vertical de la gráfica de bt. Sin embargo, la función de decaimiento exponencial en la fórmula (9) parece ser diferente. Mostraremos a continuación que la función de hecho se\(P_{0}e^{−rt}\) puede escribir en la forma\(Ab^t\) con b < 1.

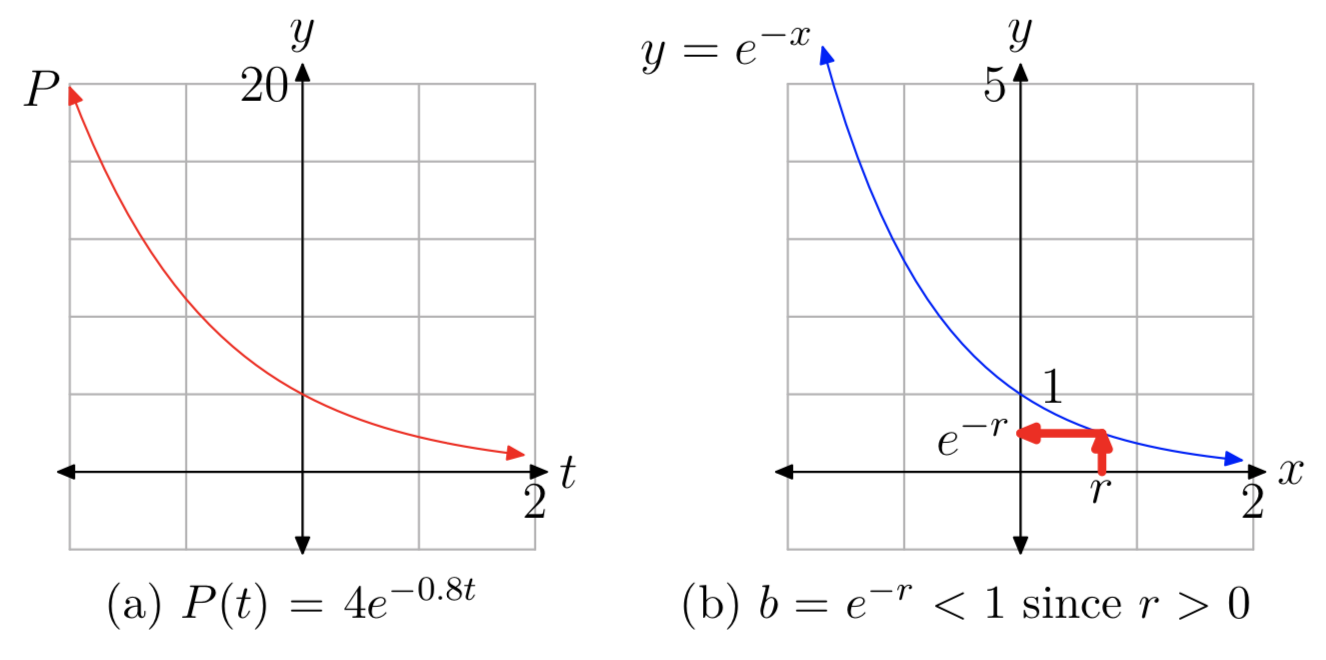
Veamos primero un ejemplo específico. Supongamos\(P(t) = 4e^{−0.8t}\). Usando las Leyes de los Exponentes, podemos reescribir P (t) como

\(P(t) = 4e^{−0.8t} = 4(e^{−0.8})^t\). (10)

Ya que\(e^{−0.8} \approx 0.44933\), de ello se deduce que

\(P(t) \approx 4(0.44933)^t\).

Debido a que la base\(\approx 0.44933\) es menor a 1, esto demuestra que P (t) es una función de decaimiento exponencial, como se ve en la Figura 2 (a)).

Ahora supongamos que P (t) es cualquier función de la forma\(P_{0}e^{−rt}\) con r > 0. Como en (10) anterior, podemos usar las Leyes de los Exponentes para reescribir P (t) como

\(P(t) = P_{0}e^{−rt} = P_{0}(e^{−r})^t = P_{0}b^t\)con\(b = e^{−r}\).

Para probar que b < 1, considere la gráfica de que\(y = e^{−x}\) se muestra en la Figura 2 (b). Ahora

\(e^{−x} = (e^{−1})^x =(\frac{1}{e})^x\)

y\(\frac{1}{e} \approx 0.36788 < 1\), así\(y = e^{−x}\) es en sí misma una curva de decaimiento exponencial. (Alternativamente, se puede observar que la gráfica de\(y = e^{−x}\) es el reflejo de la gráfica\(y = e^x\) a través del eje y.) Además, la intercepción y es (0,1) ya que\(e^{−0} = 1\). De ello se deduce que\(b = e^{−r} < 1\) desde r > 0 (ver Figura 2 (b)).

Por lo tanto, las funciones de la forma\(P(t) = P_{0}e^{−rt}\) con r > 0 son funciones de decaimiento exponencial.

Figura 2

Aplicaciones de Decaimiento Exponencial

El principal ejemplo de desintegración exponencial es la desintegración radiactiva. Los elementos e isótopos radiactivos emiten espontáneamente partículas subatómicas, y este proceso cambia gradualmente la sustancia en un isótopo diferente. Por ejemplo, el isótopo radiactivo Uranio-238 finalmente se desintegra en el isótopo estable Plomo-206. Este es un proceso aleatorio para átomos individuales, pero en general la masa de la sustancia disminuye de acuerdo con la fórmula de decaimiento exponencial (9).

Ejemplo\(\PageIndex{11}\)

Supongamos que cierto elemento radiactivo tiene una tasa de desintegración anual del 10%. Comenzando con una muestra de 200 gramos del elemento, ¿cuántos gramos quedarán en 3 años?

Este es un problema de valor futuro. Si medimos tamaño en gramos y tiempo en años, entonces\(P(t) = P_{0}e^{−rt}\) con\(P_{0} = 200\) y r = 0.10. Insertando estos valores particulares en la fórmula (9), obtenemos

\(P(t) = 200e^{−0.10t}\).

La cantidad en 3 años es de\(P(3) = 200e^{−(0.10)(3)} \approx 148.1636\) gramos.

Ejemplo\(\PageIndex{12}\)

Usando el mismo elemento que en el Ejemplo 11, si una muestra particular del elemento se descompone a 50 gramos después de 5 años, ¿qué tan grande era la muestra original?

Este es un problema de valor presente, donde lo desconocido es el monto inicial\(P_{0}\). Como antes, r = 0. 10, entonces

\(P(t) = P_{0}e^{−0.10t}\).

Desde P (5) = 50, tenemos la ecuación

\(50 = P(5) = P_{0}e^{−(0.10)(5)}\).

Esta ecuación se puede resolver por división:

\(\frac{50}{e^{−(0.10)(5)}} = P_{0}\)

Termina calculando el valor del lado izquierdo para obtener\(P_{0} \approx 82.43606\) gramos.

Ejemplo\(\PageIndex{13}\)

Supongamos que cierto isótopo radiactivo tiene una tasa de desintegración anual del 5%. ¿Cuántos años tardará una muestra de 100 gramos en decairse a 40 gramos?

Usar\(P(t) = P_{0}e^{−​​​​​​​rt}\) con\(P_{0} = 100\) and r = 0. 05, entonces\(P(t) = 100e^{−0.05t}\).

Ahora queremos saber cuándo el valor futuro P (t) del tamaño de la muestra en algún momento t será igual a 40. Por lo tanto, necesitamos resolver la ecuación P (t) = 40 para el tiempo t, lo que lleva a la ecuación exponencial

\(40 = 100e^{−0.05t}\).

Utilizando el procedimiento de resolución de ecuaciones exponenciales que se presentó en la Sección 8.6.

\(40 = 100e^{−0.05t}\)

\(\rightarrow 0.4 = e^{−0.05t}\)aislar el exponencial

\(\rightarrow ln(0.4) = ln(e^{−0.05t})\)aplicar la función de registro natural

\(\rightarrow ln(0.4) = −0.05t\)desde\(ln(e^x) = x\)

\(\rightarrow \frac{ln(0.4)}{−0.05} = t\)división

\(\rightarrow t \approx 18.32581\).

De esta manera, tardarían aproximadamente 18.33 años para que la muestra se desintegrara a 40 gramos.

Vimos antes que los procesos de crecimiento exponencial tienen un tiempo fijo de duplicación. De igual manera, los procesos de decaimiento exponencial tienen una vida media fija, el tiempo en el que la mitad de la cantidad original decae.

Ejemplo\(\PageIndex{14}\)

Usando el mismo elemento que en el Ejemplo 13, ¿cuál es la vida media del elemento?

Como antes, r = 0.05, entonces

\(P(t) = P_{0}e^{−0.05t}\).

El tamaño inicial es\(P_{0}\) gramos, por lo que queremos saber cuándo el valor futuro P (t) en algún momento t será igual a la mitad de la cantidad inicial,\(\frac{P_{0}}{2}\). Por lo tanto, necesitamos resolver la ecuación\(P(t) = \frac{P_{0}}{2}\) para el tiempo t, lo que lleva a la ecuación exponencial

\(\frac{P_{0}}{2} = P_{0}e^{−0.05t}\).

Utilizando el mismo procedimiento que en el último ejemplo,

\(\frac{P_{0}}{2} = P_{0}e^{−0.05t}\)

\(\rightarrow \frac{1}{2} = e^{−0.05t}\)aislar el exponencial

\(\rightarrow ln(\frac{1}{2}) = ln(e^{−0.05t})\)aplicar la función de registro natural

\(\rightarrow ln(\frac{1}{2}) = −0.05t\)desde\(ln(e^x) = x\)

\(\rightarrow \frac{ln(\frac{1}{2})}{−0.05} = t\)división

\(\rightarrow t \approx 13.86294\)

Así, la vida media es de aproximadamente 13.86 años.

El proceso de desintegración radiactiva también forma la base de la técnica de datación por carbono-14. La atmósfera terrestre contiene una pequeña cantidad del isótopo radiactivo carbono-14, y por lo tanto las plantas y los animales también contienen algo de carbono-14 debido a su interacción con la atmósfera. Sin embargo, esta interacción termina cuando una planta o animal muere, por lo que el carbono-14 comienza a descomponerse (la tasa de descomposición es de 0.012%). Al comparar la cantidad de carbono-14 en un hueso, por ejemplo, con la cantidad normal en un animal vivo, los científicos pueden calcular la edad del hueso.

Ejemplo\(\PageIndex{15}\)

Supongamos que sólo 1.5% de la cantidad normal de carbono-14 permanece en un fragmento de hueso. ¿Qué edad tiene el hueso?

Usar\(P(t) = P_{0}e^{−rt}\) con r = 0.00012, entonces

\(P(t) = P_{0}e^{−0.00012t}\).

El tamaño inicial es\(P_{0}\) gramos, por lo que queremos saber cuándo el valor futuro P (t) en algún momento t será igual a 1.5% de la cantidad inicial,\(0.015P_{0}\). Por lo tanto, necesitamos resolver la ecuación\(P(t) = 0.015P_{0}\) para el tiempo t, lo que lleva a la ecuación exponencial

\(0.015P_{0} = P_{0}e^{−0.00012t}\).

Utilizando el mismo procedimiento que en el Ejemplo 14,

\(0.015P_{0} = P_{0}e^{−0.00012t}\)

\(\rightarrow 0.015 = e^{−0.00012t}\)aislar el exponencial

\(\rightarrow ln(0.015) = ln(e^{−0.00012t})\)aplicar la función de registro natural

\(\rightarrow ln(0.015) = −0.00012t\)desde\(ln(e^x) = x\)

\(\rightarrow \frac{ln(0.015)}{−0.00012} = t\)división

\(\rightarrow t \approx 34998\)

Así, el hueso tiene aproximadamente 34998 años de edad.

Si bien la técnica del carbono-14 sólo funciona en plantas y animales, existen otras técnicas similares de datación, utilizando otros isótopos radiactivos, que se utilizan para fechar rocas y otra materia inorgánica.

Ejercicio

Ejercicio\(\PageIndex{1}\)

Supongamos que la población de un determinado pueblo crece a una tasa anual del 6%. Si actualmente la población es de 5, 000, ¿cuál será en 7 años? Redondee su respuesta al entero más cercano.

Contestar

7610 personas

Ejercicio\(\PageIndex{2}\)

Supongamos que la población de un determinado pueblo crece a una tasa anual del 5%. Si actualmente la población es de 2 mil, ¿cuántos años tardará en duplicarse? Redondee su respuesta a la centésima más cercana.

Ejercicio\(\PageIndex{3}\)

Supongamos que cierto isótopo radiactivo tiene una tasa de desintegración anual de 7.2%. ¿Cuántos años tardará una muestra de 227 gramos en desintegrarse a 93 gramos? Redondee su respuesta a la centésima más cercana.

Contestar

12. 39 años

Ejercicio\(\PageIndex{4}\)

Supongamos que cierto isótopo radiactivo tiene una tasa de desintegración anual de 6.8%. ¿Cuántos años tardará una muestra de 399 gramos en decairse a 157 gramos? Redondee su respuesta a la centésima más cercana.

Ejercicio\(\PageIndex{5}\)

Supongamos que la población de un determinado pueblo crece a una tasa anual de 8%. Si actualmente la población es de 4 mil, ¿cuántos años tardará en duplicarse? Redondee su respuesta a la centésima más cercana.

Contestar

8. 66 años

Ejercicio\(\PageIndex{6}\)

Supongamos que cierto isótopo radiactivo tiene una tasa de desintegración anual de 19.2%. Comenzando con una muestra de 443 gramos, ¿cuántos gramos quedarán después de 9 años? Redondee su respuesta a la centésima más cercana.

Ejercicio\(\PageIndex{7}\)

Supongamos que cierto isótopo radiactivo tiene una tasa de desintegración anual de 17.4%. ¿Cuál es la vida media (en años) del isótopo? Redondee su respuesta a la centésima más cercana.

Contestar

3. 98 años

Ejercicio\(\PageIndex{8}\)

Supongamos que la población de un determinado pueblo crece a una tasa anual del 7%. Si actualmente la población es de 8 mil, ¿cuántos años tardará en llegar a los 18 mil? Redondee su respuesta a la centésima más cercana.

Ejercicio\(\PageIndex{9}\)

Supongamos que cierto isótopo radiactivo tiene una tasa de desintegración anual de 17.3%. Comenzando con una muestra de 214 gramos, ¿cuántos gramos quedarán después de 5 años? Redondee su respuesta a la centésima más cercana.

Contestar

90. 11g

Ejercicio\(\PageIndex{10}\)

Supongamos que la población de un determinado pueblo crece a una tasa anual del 7%. Si la población crece a 2, 000 en 7 años, ¿cuál fue la población original? Redondee su respuesta al entero más cercano.

Ejercicio\(\PageIndex{11}\)

Supongamos que la población de un determinado pueblo crece a una tasa anual de 3%. Si actualmente la población es de 3 mil, ¿cuántos años tardará en duplicarse? Redondee su respuesta a la centésima más cercana.

Contestar

23. 10 años

Ejercicio\(\PageIndex{12}\)

Supongamos que cierto isótopo radiactivo tiene una tasa de desintegración anual de 12.5%. Comenzando con una muestra de 127 gramos, ¿cuántos gramos quedarán después de 6 años? Redondee su respuesta a la centésima más cercana.

Ejercicio\(\PageIndex{13}\)

Supongamos que cierto isótopo radiactivo tiene una tasa de desintegración anual de 13.1%. Supongamos que cierto isótopo radiactivo tiene una tasa de desintegración anual de 13.1%

Contestar

141. 10g

Ejercicio\(\PageIndex{14}\)

Supongamos que la población de un determinado pueblo crece a una tasa anual del 2%. Si la población crece a 9, 000 en 4 años, ¿cuál era la población original? Redondee su respuesta al entero más cercano.

Ejercicio\(\PageIndex{15}\)

Supongamos que la población de un determinado pueblo crece a una tasa anual del 2%. Si actualmente la población es de 7 mil, ¿cuántos años tardará en duplicarse? Redondee su respuesta a la centésima más cercana.

Contestar

34. 66 años

Ejercicio\(\PageIndex{16}\)

Supongamos que cierto isótopo radiactivo tiene una tasa de desintegración anual de 5.3%. ¿Cuántos años tardará una muestra de 217 gramos en desintegrarse a 84 gramos? Redondee su respuesta a la centésima más cercana.

Ejercicio\(\PageIndex{17}\)

Supongamos que cierto isótopo radiactivo tiene una tasa de desintegración anual de 18.7%. ¿Cuántos años tardará una muestra de 324 gramos en desintegrarse a 163 gramos? Redondee su respuesta a la centésima más cercana.

Contestar

3. 67 años

Ejercicio\(\PageIndex{18}\)

Supongamos que la población de un determinado pueblo crece a una tasa anual de 8%. Si actualmente la población es de 8 mil, ¿cuántos años tardará en llegar a los 18 mil? Redondee su respuesta a la centésima más cercana.

Ejercicio\(\PageIndex{19}\)

Supongamos que cierto isótopo radiactivo tiene una tasa de desintegración anual de 2.3%. Si una muestra en particular se descompone a 25 gramos después de 8 años, ¿qué tan grande (en gramos) era la muestra original? Redondee su respuesta a la centésima más cercana.

Contestar

30. 05g

Ejercicio\(\PageIndex{20}\)

Supongamos que la población de un determinado pueblo crece a una tasa anual de 4%. Si actualmente la población es de 7 mil, ¿cuántos años tardará en llegar a los 17 mil? Redondee su respuesta a la centésima más cercana.

Ejercicio\(\PageIndex{21}\)

Supongamos que cierto isótopo radiactivo tiene una tasa de desintegración anual de 9.8%. Si una muestra en particular se descompone a 11 gramos después de 6 años, ¿qué tan grande (en gramos) era la muestra original? Redondee su respuesta a la centésima más cercana.

Contestar

19. 80g

Ejercicio\(\PageIndex{22}\)

Supongamos que la población de un determinado pueblo crece a una tasa anual del 5%. Si la población crece a 6, 000 en 3 años, ¿cuál era la población original? Redondee su respuesta al entero más cercano.

Ejercicio\(\PageIndex{23}\)

Supongamos que la población de un determinado pueblo crece a una tasa anual de 8%. Si actualmente la población es de 6, 000, ¿qué será en 5 años? Redondee su respuesta al entero más cercano.

Contestar

8, 951 personas

Ejercicio\(\PageIndex{24}\)

Supongamos que cierto isótopo radiactivo tiene una tasa de desintegración anual de 15.8%. ¿Cuál es la vida media (en años) del isótopo? Redondee su respuesta a la centésima más cercana.

Ejercicio\(\PageIndex{25}\)

Supongamos que la población de un determinado pueblo crece a una tasa anual del 9%. Si la población crece a 7, 000 en 5 años, ¿cuál era la población original? Redondee su respuesta al entero más cercano.

Contestar

8, 951 personas

Ejercicio\(\PageIndex{26}\)

Supongamos que cierto isótopo radiactivo tiene una tasa de desintegración anual de 18.6%. Si una muestra en particular se descompone a 41 gramos después de 3 años, ¿qué tan grande (en gramos) era la muestra original? Redondee su respuesta a la centésima más cercana.

Ejercicio\(\PageIndex{27}\)

Supongamos que cierto isótopo radiactivo tiene una tasa de desintegración anual de 5.2%. ¿Cuál es la vida media (en años) del isótopo? Redondee su respuesta a la centésima más cercana.

Contestar

13. 33 años

Ejercicio\(\PageIndex{28}\)

Supongamos que cierto isótopo radiactivo tiene una tasa de desintegración anual de 6.5%. ¿Cuál es la vida media (en años) del isótopo? Redondee su respuesta a la centésima más cercana.

Ejercicio\(\PageIndex{29}\)

Supongamos que la población de un determinado pueblo crece a una tasa anual de 8%. Si actualmente la población es de 2 mil, ¿cuántos años tardará en llegar a los 7 mil? Redondee su respuesta a la centésima más cercana.

Contestar

15. 66 años

Ejercicio\(\PageIndex{30}\)

Supongamos que cierto isótopo radiactivo tiene una tasa de desintegración anual de 3.7%. Si una muestra en particular se descompone a 47 gramos después de 8 años, ¿qué tan grande (en gramos) era la muestra original? Redondee su respuesta a la centésima más cercana.

Ejercicio\(\PageIndex{31}\)

Supongamos que la población de un determinado pueblo crece a una tasa anual del 6%. Si actualmente la población es de 7, 000, ¿qué será en 7 años? Redondee su respuesta al entero más cercano.

Contestar

10, 654 personas

Ejercicio\(\PageIndex{32}\)

Supongamos que la población de un determinado pueblo crece a una tasa anual de 4%. Si actualmente la población es de 1, 000, ¿cuál será en 3 años? Redondee su respuesta al entero más cercano.

En los Ejercicios 33 - 40, utilice el hecho de que la tasa de desintegración del carbono-14 es de 0.012%. Redondee su respuesta al año más cercano.

Ejercicio\(\PageIndex{33}\)

Supongamos que sólo 8.6% de la cantidad normal de carbono-14 permanece en un fragmento de hueso. ¿Qué edad tiene el hueso?

Contestar

20445 años

Ejercicio\(\PageIndex{34}\)

Supongamos que sólo 5.2% de la cantidad normal de carbono-14 permanece en un fragmento de hueso. ¿Qué edad tiene el hueso?

Ejercicio\(\PageIndex{35}\)

Supongamos que 90.1% de la cantidad normal de carbono-14 permanece en una pieza de madera. ¿Qué edad tiene la madera?

Contestar

869 años

Ejercicio\(\PageIndex{36}\)

Supongamos que 83.6% de la cantidad normal de carbono-14 permanece en un trozo de tela. ¿Qué edad tiene la tela?

Ejercicio\(\PageIndex{37}\)

Supongamos que solo el 6.2% de la cantidad normal de carbono-14 permanece en un fragmento de hueso. ¿Qué edad tiene el hueso?

Contestar

23172 años

Ejercicio\(\PageIndex{38}\)

Supongamos que sólo 1.3% de la cantidad normal de carbono-14 permanece en un fragmento de hueso. ¿Qué edad tiene el hueso?

Ejercicio\(\PageIndex{39}\)

Supongamos que 96.7% de la cantidad normal de carbono-14 permanece en un trozo de tela. ¿Qué edad tiene la tela?

Contestar

280 años

Ejercicio\(\PageIndex{40}\)

Supongamos que 84.9% de la cantidad normal de carbono-14 permanece en una pieza de madera. ¿Qué edad tiene la madera?

​​​​​​​