8.6: Propiedades de logaritmos; Resolviendo Ecuaciones Exponenciales

Última actualización
Guardar como PDF

Page ID: 110676

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Los logaritmos fueron descubiertos y utilizados en la antigüedad por matemáticos indios e islámicos. Sin embargo, no se utilizaron ampliamente hasta la década de 1600, cuando los logaritmos simplificaron las grandes cantidades de cálculos manuales necesarios en las exploraciones científicas de la época. En particular, después de la invención del telescopio, los cálculos que involucraban datos astronómicos se volvieron muy importantes, y los logaritmos se convirtieron en una herramienta matemática esencial. En efecto, hasta la invención de la computadora y la calculadora electrónica en los últimos tiempos, los cálculos manuales utilizando logaritmos eran un elemento básico del plan de estudios de cada estudiante de ciencias.

La utilidad de los logaritmos en los cálculos se basa en las siguientes tres propiedades importantes, conocidas generalmente como las propiedades de logaritmos.

PROPIEDAD DE LOGARITMOS

(a)$log_{b}(MN) = log_{b}(M)+log_{b}(N)$

b)$log_{b}(\frac{M}{N}) = log_{b}(M)−log_{b}(N)$

c)$log_{b}(M^r)=rlog_{b}(M)$

siempre que M, N, b > 0.

El primer inmueble dice que el “tronco de un producto es la suma de los troncos”. El segundo dice que el “registro de un cociente es la diferencia de los troncos”. Y a la tercera propiedad se le hace referencia a veces como la “regla del poder”. Hablando libremente, al tomar el registro de una potencia, puedes simplemente mover al exponente frente al tronco.

No entraremos en los detalles de los procedimientos de cómputos utilizando las propiedades (a) y (b), ya que estos procedimientos ya no son necesarios después de la invención de la calculadora. Pero la idea es que un producto que consume mucho tiempo de dos números, por ejemplo dos números de 10 dígitos, pueda transformarse por la propiedad (a) en un problema de adición mucho más simple. Del mismo modo, un cociente grande y difícil puede transformarse por la propiedad (b) en un problema de resta mucho más simple. Las propiedades (a) y (b) también son la base de la regla de cálculo, un dispositivo de cómputo mecánico que precedió a la calculadora electrónica (muy rápido y útil, pero solo exacto de aproximadamente tres dígitos).

La propiedad (c), por otra parte, sigue siendo útil para cálculos difíciles. Si intentas calcular una potencia grande, digamos 2100, en una calculadora o computadora, recibirás un mensaje de error. Eso se debe a que todas las calculadoras y computadoras solo pueden manejar números y exponentes dentro de un cierto rango. Entonces, para calcular una gran potencia, es necesario usar la propiedad (c) para convertirla en un problema de multiplicación. Los detalles de este trámite se dan en la Sección 8.8.

A pesar de que las propiedades (a) y (b) ya no son necesarias para fines de cálculo, eso no significa que no sean importantes. Las funciones logarítmicas sirven para muchos propósitos en matemáticas y ciencias, y todas las propiedades logarítmicas son útiles de diversas maneras.

¿De dónde provienen las propiedades del logaritmo? En realidad, todos se derivan de las leyes de los exponentes, utilizando el hecho de que la función exponencial es la inversa de la función logaritmo. Dado que solo usaremos la propiedad (c) en este libro, mostraremos cómo se deriva esa propiedad. Las propiedades (a) y (b) se derivan de manera similar.

Prueba de (c): Comience en el lado derecho de la ecuación, y etiquete$log_{b}(M)$ por x:

$x = log_{b}(M)$

Use la Definición 1 en la Sección 8.5 para reescribir la ecuación en forma exponencial:

$b^x = M$

Levante ambos lados a la potencia résima:

$(b^x)^r =M^r$

Aplica una de las Leyes de los Exponentes al lado izquierdo:

$b^{rx} = M^r$

Aplicar la función logarítmica base b a ambos lados:

$log_{b}(b^rx) = log_{b}(M^r)$

Aplica la fórmula (10) en la Sección 8.5 al lado izquierdo:

$rx = log_{b}(M^r)$

Sustituya la parte posterior por x desde la primera línea de arriba:

$rlog_{b}(M) = log_{b}(M^r)$

Esta es la fórmula en la propiedad (c).

Cambio de Fórmula Base

Ahora podemos probar una fórmula de conversión que nos permitirá calcular el logaritmo a cualquier base.

Cambio de fórmula base

$log_{a}(x) = \frac{log_{b}(x)}{log_{b}(a)}$

Prueba: Comience en el lado izquierdo de la ecuación y etiquete$log_{a}(x)$ por r:

$r = log_{a}(x)$

Use la Definición 1 en la Sección 8.5 para reescribir la ecuación en forma exponencial:

$a^r = x$

Aplicar la función logarítmica base b a ambos lados:

$log_{b}(a^r) = log_{b}(x)$

Aplicar la propiedad (c) al lado izquierdo:

$rlog_{b}(a) = log_{b}(x)$

Dividir por$log_{b}(a)$:

$r = \frac{log_{b}(x)}{log_{b}(a)}$

Sustituir de nuevo por r desde la primera línea de arriba:

$log_{a}(x) = \frac{log_{b}(x)}{log_{b}(a)}$

Este es el Cambio de Fórmula Base.

Ejemplo$\PageIndex{1}$

Cómpela$log_{2}(5)$.

Antes de aplicar el Cambio de Fórmula Base, veamos si podemos estimar el valor de$log_{2}(5)$. Primer recuerdo del Inmueble 9 en la Sección 8.5 que$2^{log_{2}(5)} = 5$. Ahora, ¿qué tan grande tendría que ser el exponente sobre una base de 2 para que la potencia iguale 5? Dado que$2^2 = 4$ (demasiado pequeño) y$2^3 = 8$ (demasiado grande), debemos$log_{2}(5)$ esperar estar en algún lugar entre 2 y 3. De hecho, aplicar la Fórmula de Cambio de Base con los rendimientos logaritmos comunes

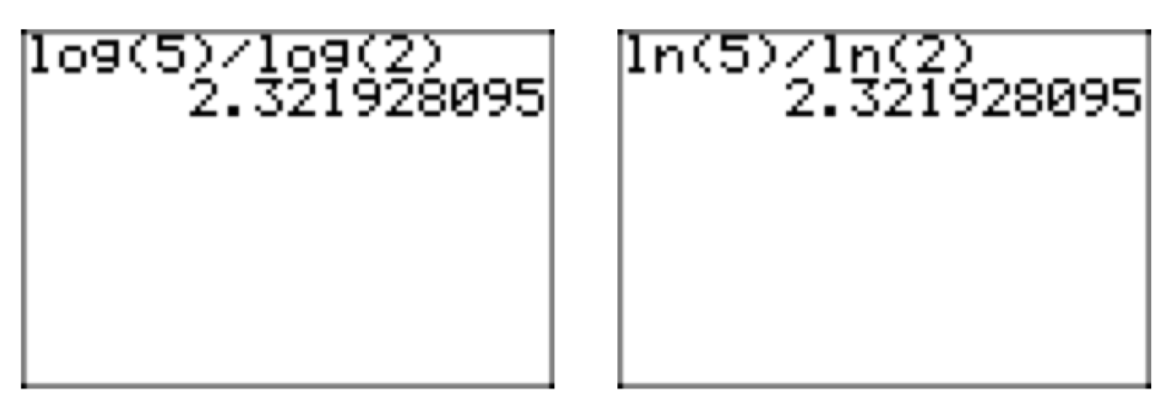
$log_{2}(5) = \frac{log_{10}(5)}{log_{10}(5)} = \frac{log(5)}{log(2)} \approx \frac{.6989700043}{.3010299957} \approx 2.321928095$.

Según la fórmula, podríamos usar el logaritmo natural para obtener la misma respuesta, como en

$log_{2}(5) = \frac{log_{e}(5)}{log_{e}(2)} = \frac{ln(5)}{ln(2)} \approx \frac{1.609437912}{.6931471806} \approx 2.321928095$.

Las pulsaciones de teclas de la calculadora se muestran en la Figura 1

Figura 1. Computación$log_{2}(5)$ mediante la Fórmula de Cambio de Base.

Screen Shot 2019-08-14 en 4.09.49 PM.png — Figura 1. Computación$log_{2}(5)$ mediante la Fórmula de Cambio de Base.

Otra forma de ver el Cambio de Fórmula Base es que dice que todos los logaritmos son múltiplos entre sí, ya que

$log_{a}(x) = (\frac{1}{log_{b}(a)})log_{b}(x)$.

Así,$log_{a}(x)$ es un múltiplo constante de$log_{b}(x)$, donde está la constante$\frac{1}{log_{b}(a)}$.

Resolver ecuaciones exponenciales

La propiedad (c) ($log_{b}(M^r) = r log_{b}(M)$) también se usa ampliamente para ayudar a resolver ecuaciones exponenciales, y por lo tanto será una herramienta importante cuando trabajemos con aplicaciones en la siguiente sección. En términos generales, la estrategia principal para resolver ecuaciones exponenciales es (1) aislar primero la exponencial, luego (2) aplicar una función logarítmica a ambos lados, y luego (3) usar la propiedad (c). Ilustraremos la estrategia con varios ejemplos.

Ejemplo$\PageIndex{2}$

Resolver$8 = 5(3^x)$.

Antes de probar el procedimiento descrito anteriormente, primero aproximemos la solución usando un enfoque gráfico. Grafica ambos lados de la ecuación en tu calculadora, y luego encuentra la intersección de las dos curvas para obtener$x \approx 0.42781574$ (ver Figura 2).

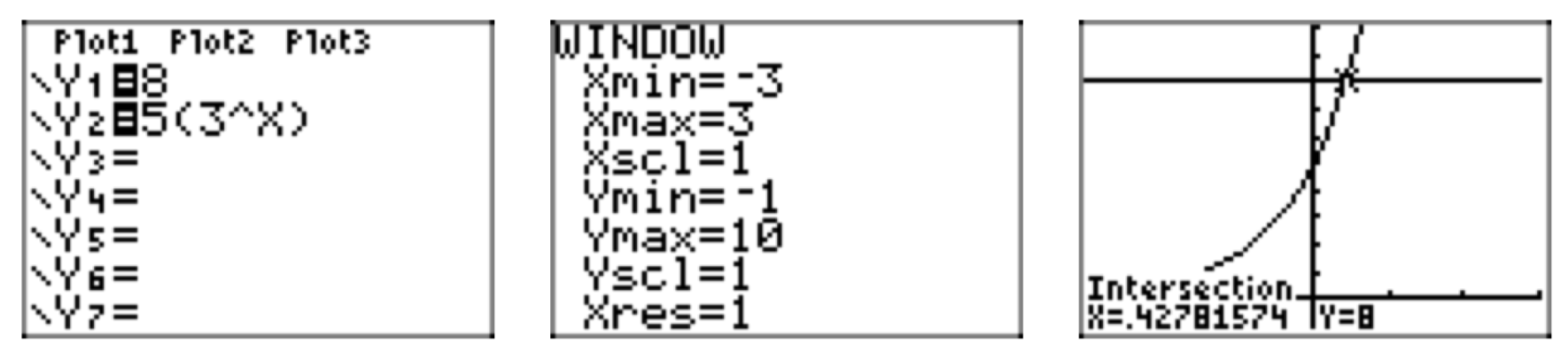
Screen Shot 2019-08-14 a las 4.14.18 PM.png — Figura 2. Aproximando la solución de$8 = 5(3^x)$ gráficamente.

Ahora resolveremos la ecuación algebraicamente. Primero aísle la función exponencial en un lado de la ecuación dividiendo ambos lados por 5:

$1.6 = 3^x$

Después toma el logaritmo de ambos lados. Utilice el registro común o natural:

$log(1.6) = log(3^x)$

Ahora use la propiedad (c) para mover el exponente frente al tronco en el lado derecho:

log (1.6) = xlog (3)

Finalmente, resuelve para x dividiendo ambos lados por tronco (3):

$\frac{log(1.6)}{log(3)} = x$

Así, el valor exacto de x es$\frac{log(1.6)}{log(3)}$, y el valor aproximado es 0.42781574. Tenga en cuenta que esto es lo mismo que la aproximación gráfica encontrada anteriormente.

Ejemplo$\PageIndex{3}$

Resolver$300 = 100(1.05^{5x})$.

$300 = 100(1.05^{5x})$

$\rightarrow 3 = 1.05^{5x}$aislar el exponencial

$\rightarrow log(3) = log(1.05^{5x})$aplicar la función de registro común

$\rightarrow log(3) = 5x log(1.05)$usar propiedad (c)

$\rightarrow \frac{log(3)}{5log(1.05)} = x$dividir

$\rightarrow x \approx 4.503417061$

Si la base del exponencial es 10 o e, la elección correcta del logaritmo conduce a una solución más rápida:

Ejemplo$\PageIndex{4}$

Resolver$3 = 4e^x$.

$3 = 4e^x$.

$\rightarrow 0.75 = e^x$aislar el exponencial

$\rightarrow ln(0.75) = ln(e^x)$aplicar la función de registro natural

$\rightarrow ln(0.75) = x$desde$ln(e^x) = x$

$\rightarrow x \approx −.2876820725$

En este caso, debido a que la base de la función exponencial es e, el uso de la función logarítmica natural simplifica la solución.

Ahora podemos dirigir nuestra atención a resolver problemas de aplicación más interesantes, como las preguntas planteadas al final de la Sección 8.3.

Ejemplo$\PageIndex{5}$

Si depositas $1000 en una cuenta pagando 6% de intereses compuestos continuamente, ¿cuánto tiempo tardarás en tener 1500 dólares en tu cuenta?

Primero, recuerde la fórmula de interés compuesto continuo de la Sección 8.3:

$P(t) = P_{0}e^{rt}$(6)

En este caso,$P_{0} = 1000$ y r = .06. Insertando estos valores en la fórmula, obtenemos

$P(t) = 1000e^{0.06t}$.

Ahora queremos que el valor futuro P (t) de la cuenta en algún momento t sea igual a 1500 dólares. Por lo tanto, debemos resolver la ecuación

$1500 = 1000e^{0.06t}$.

Siguiendo los pasos del ejemplo anterior,

$1500 = 1000e^{0.06t}$

$\rightarrow 1.5 = e^{0.06t}$aislar el exponencial

$\rightarrow ln(1.5) = ln(e^{0.06t})$aplicar la función de registro natural

$\rightarrow ln(1.5) = 0.06t$desde$ln(e^x) = x$

$\rightarrow \frac{ln(1.5)}{0.06} = t$dividir

$\rightarrow t \approx 6.757751802$

Así, tomaría alrededor de 6 años y 9 meses.

Ejemplo$\PageIndex{7}$

Si depositas $1000 en una cuenta pagando 5% de interés compuesto mensualmente, ¿cuánto tiempo tardará tu dinero en duplicarse?

Primero, recuerde la fórmula de interés compuesto discreto de la Sección 8.3:

$P(t) = P_{0}(1+\frac{r}{n})^{nt}$(8)

En este caso,$P_{0} = 1000$, r = .05, y n = 12. Insertando estos valores en la fórmula, obtenemos

$P(t) = 1000(1+\frac{.05}{12})^{12t}$.

Ahora queremos que el valor futuro P (t) de la cuenta en algún momento t sea igual al doble del monto inicial. En otras palabras, queremos que P (t) sea igual a 2000. Por lo tanto, debemos resolver la ecuación

$2000 = 1000(1+\frac{.05}{12})^{12t}$.

Siguiendo los pasos de los Ejemplos 2 y 3,

$2000 = 1000(1+\frac{.05}{12})^{12t}$

$\rightarrow 2 = (1+\frac{.05}{12})^{12t}$aislar el exponencial

$\rightarrow log(2) = log((1+\frac{.05}{12})^{12t})$aplicar la función de registro común

$\rightarrow log(2) = 12tlog(1+\frac{.05}{12})$usar propiedad (c)

$\rightarrow \frac{log(2)}{12log(1+\frac{.05}{12})} = t$dividir

$\rightarrow t \approx 13.89180573$

Así, tardarían alrededor de 13.9 años para que tu dinero se duplicara.

Ejercicio

En los Ejercicios 1 - 10, utilice una calculadora para evaluar la función al valor dado p. Redondee su respuesta a la centésima más cercana.

Ejercicio$\PageIndex{1}$

$f(x) = log_{4}(x)$; p = 57.60.

Contestar: 2. 92

Ejercicio$\PageIndex{2}$

$f(x) = log_{4}(x)$; p = 11.22.

Ejercicio$\PageIndex{3}$

$f(x) = log_{7}(x)$; p = 2.98.

Contestar: 0. 56

Ejercicio$\PageIndex{4}$

$f(x) = log_{3}(x)$; p = 2.27.

Ejercicio$\PageIndex{5}$

$f(x) = log_{6}(x)$; p = 2.56.

Contestar: 0. 52

Ejercicio$\PageIndex{6}$

$f(x) = log_{8}(x)$; p = 289.27.

Ejercicio$\PageIndex{7}$

$f(x) = log_{8}(x)$; p = 302.67.

Contestar: 2. 75

Ejercicio$\PageIndex{8}$

$f(x) = log_{5}(x)$; p = 15.70.

Ejercicio$\PageIndex{9}$

$f(x) = log_{8}(x)$; p = 46.13.

Contestar: 1. 84

Ejercicio$\PageIndex{10}$

$f(x) = log_{4}(x)$; p = 15.59.

En los Ejercicios 11 - 18, realizar cada una de las siguientes tareas.

Aproxime la solución de la ecuación dada usando su calculadora gráfica. Cargue cada lado de la ecuación en el menú Y= de su calculadora. Ajuste los parámetros VENTANA para que el punto de intersección de las gráficas sea visible en la ventana de visualización. Utilice la utilidad de intersección en el menú CALC de su calculadora para determinar la coordenada x del punto de intersección. Luego haga una copia exacta de la imagen en su ventana de visualización en su papel de tarea.
Resuelve algebraicamente la ecuación dada y redondea tu respuesta a la centésima más cercana.

Ejercicio$\PageIndex{11}$

$20 = 3(1.2)^x$

Contestar

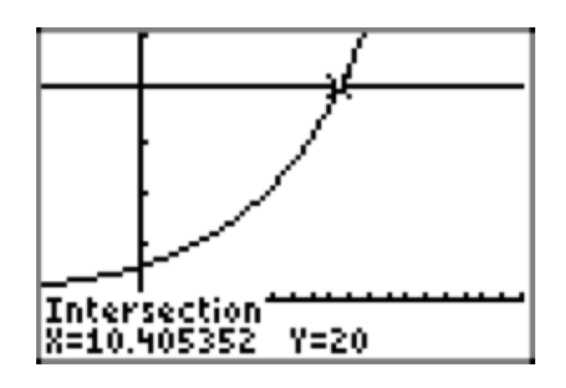
$Screen Shot 2019-08-15 en 2.26.22 PM.png$
10. 41

Ejercicio$\PageIndex{12}$

$15 = 2(1.8)^x$

Ejercicio$\PageIndex{13}$

$14 = (1.4)^{5x}$

Contestar

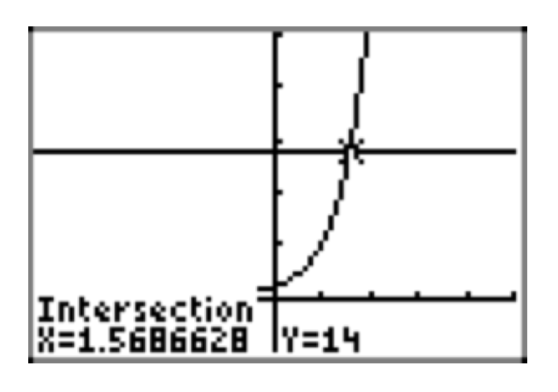
$Screen Shot 2019-08-15 a las 2.27.17 PM.png$
1. 57

Ejercicio$\PageIndex{14}$

$16 = (1.8)^{4x}$

Ejercicio$\PageIndex{15}$

$−4 = 0.2^x−9$

Contestar

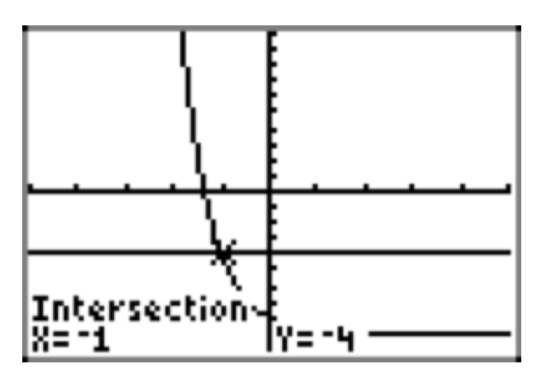
$Screen Shot 2019-08-15 a 2.30.00 PM.png$
− 1. 00

Ejercicio$\PageIndex{16}$

$12 = 2.9^x+2$

Ejercicio$\PageIndex{17}$

$13 = 0.1^{x+1}$

Contestar

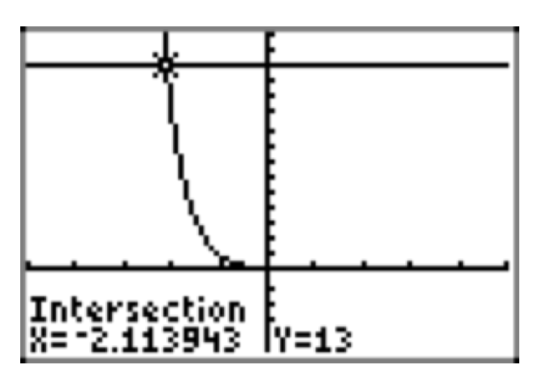
$Screen Shot 2019-08-15 en 2.30.59 PM.png$
− 2. 11

Ejercicio$\PageIndex{18}$

$19 = 1.2^{x−6}$

En los Ejercicios 19 - 34, resuelve algebraicamente la ecuación dada, y redondea tu respuesta a la centésima más cercana.

Ejercicio$\PageIndex{19}$

$20 = e^{x−3}$

Contestar: 6. 00

Ejercicio$\PageIndex{20}$

$−4 = e^x−9$

Ejercicio$\PageIndex{21}$

$23 = 0.9^x+9$

Contestar: − 25. 05

Ejercicio$\PageIndex{22}$

$10 = e^x+7$

Ejercicio$\PageIndex{23}$

$19 = e^x+5$

Contestar: 2. 64

Ejercicio$\PageIndex{24}$

$4 = 7(2.3)^x$

Ejercicio$\PageIndex{25}$

$18 = e^{x+4}$

Contestar: − 1. 11

Ejercicio$\PageIndex{26}$

$15 = e^{x+6}$

Ejercicio$\PageIndex{27}$

$8 = 2.7^{3x}$

Contestar: 0. 70

Ejercicio$\PageIndex{28}$

$7 = e^x+1$

Ejercicio$\PageIndex{29}$

$7 = 1.1^{8x}$

Contestar: 2. 55

Ejercicio$\PageIndex{30}$

$6 = 0.2^{x−8}$

Ejercicio$\PageIndex{31}$

$−7 = 1.3^{x−9}$

Contestar: 2. 64

Ejercicio$\PageIndex{32}$

$11 = 3(0.7)^x$

Ejercicio$\PageIndex{33}$

$23 = e^x+9$

Contestar: 2. 64

Ejercicio$\PageIndex{34}$

$20 = 3.2^{x+1}$

Ejercicio$\PageIndex{35}$

Supongamos que invierte $17,000 al 6% de interés compuesto diariamente. ¿Cuántos años tardará en duplicarse su inversión? Redondee su respuesta a la centésima más cercana.

Contestar: 11. 55 años

Ejercicio$\PageIndex{36}$

Supongamos que invierte $6,000 al 9% de interés compuesto continuamente. ¿Cuántos años tardará en duplicarse su inversión? Redondee su respuesta a la centésima más cercana.

Ejercicio$\PageIndex{37}$

Supongamos que invierte $16,000 al 6% de interés compuesto diariamente. ¿Cuántos años tardará en que su inversión llegue a los 26,000 dólares? Redondee su respuesta a la centésima más cercana.

Contestar: 8. 09 años

Ejercicio$\PageIndex{38}$

Supongamos que invierte $15,000 al 5% de interés compuesto mensualmente. ¿Cuántos años tardará en duplicarse su inversión? Redondee su respuesta a la centésima más cercana.

Ejercicio$\PageIndex{39}$

Supongamos que invierte $18,000 al 3% de interés compuesto mensualmente. ¿Cuántos años tardará en duplicarse su inversión? Redondee su respuesta a la centésima más cercana.

Contestar: 23. 13 años

Ejercicio$\PageIndex{40}$

Supongamos que invierte $7,000 al 5% de interés compuesto diariamente. ¿Cuántos años tardará en que su inversión llegue a los 13,000 dólares? Redondee su respuesta a la centésima más cercana.

Ejercicio$\PageIndex{41}$

Supongamos que invierte $16,000 al 9% de interés compuesto continuamente. ¿Cuántos años tardará en duplicarse su inversión? Redondee su respuesta a la centésima más cercana.

Contestar: 7. 70 años

Ejercicio$\PageIndex{42}$

Supongamos que invierte $16,000 a 2% de interés compuesto continuamente. ¿Cuántos años tardará en que su inversión alcance los $25,000? Redondee su respuesta a la centésima más cercana.

Ejercicio$\PageIndex{43}$

Supongamos que invierte $2,000 al 5% de interés compuesto continuamente. ¿Cuántos años tardará en que su inversión llegue a los 10.000 dólares? Redondee su respuesta a la centésima más cercana.

Contestar: 32. 19 años

Ejercicio$\PageIndex{44}$

Supongamos que invierte $4,000 al 6% de interés compuesto continuamente. ¿Cuántos años tardará en que su inversión llegue a los 10.000 dólares? Redondee su respuesta a la centésima más cercana.

Ejercicio$\PageIndex{45}$

Supongamos que inviertes $4,000 a 3% de interés compuesto diariamente. ¿Cuántos años tardará en que su inversión llegue a los $14,000? Redondee su respuesta a la centésima más cercana.

Contestar: 41. 76 años

Ejercicio$\PageIndex{46}$

Supongamos que invierte $13,000 a 2% de interés compuesto mensualmente. ¿Cuántos años tardará en que su inversión llegue a los 20,000 dólares? Redondee su respuesta a la centésima más cercana.

Ejercicio$\PageIndex{47}$

Supongamos que invierte 20,000 dólares al 7% de interés compuesto continuamente. ¿Cuántos años tardará su inversión en llegar a los 30,000 dólares? Redondee su respuesta a la centésima más cercana.

Contestar: 5. 79 años

Ejercicio$\PageIndex{48}$

Supongamos que invierte $16,000 a 4% de interés compuesto continuamente. ¿Cuántos años tardará en duplicarse su inversión? Redondee su respuesta a la centésima más cercana.

Ejercicio$\PageIndex{49}$

Supongamos que invierte $8,000 a 8% de interés compuesto continuamente. ¿Cuántos años tardará en duplicarse su inversión? Redondee su respuesta a la centésima más cercana.

Contestar: 8. 66 años

Ejercicio$\PageIndex{50}$

Supongamos que inviertes $3,000 a 3% de interés compuesto diariamente. ¿Cuántos años tardará en duplicarse su inversión? Redondee su respuesta a la centésima más cercana.