2.7E: Ejercicios

Última actualización
Guardar como PDF

Page ID: 112764

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La práctica hace la perfección

Resolver desigualdades compuestas con “y”

En los siguientes ejercicios, resuelve cada desigualdad, grafica la solución y escribe la solución en notación de intervalos.

1. $x<3$y$x\geq 1$

2. $x\leq 4$y$x>−2$

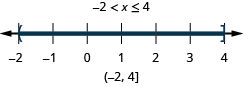
Contestar: $La solución es negativa 2 es menor que x que es menor o igual a 4. Su gráfica tiene un círculo abierto en 1negativo 2 y un círculo cerrado en 4 con sombreado entre los círculos abierto y cerrado. Su notación de intervalo es negativa 2 a 4 dentro de un paréntesis y un paréntesis.$

3. $x\geq −4$y$x\leq −1$

4. $x>−6$y$x<−3$

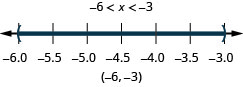
Contestar: $La solución es negativa 6 es menor que x que es menor que negativa 3. Su gráfica tiene un círculo abierto en negativo 6 y un círculo abierto en negativo 3 con sombreado entre círculos abiertos. Su notación de intervalo es negativa 6 a negativa 3 entre paréntesis.$

5. $5x−2<8$y$6x+9\geq 3$

6. $4x−1<7$y$2x+8\geq 4$

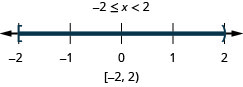
Contestar: $La solución es negativa 2 es menor o igual a x que es menor que 2. Su gráfica tiene un círculo cerrado en negativo 2 y un círculo abierto en 2 con sombreado entre los círculos cerrado y abierto. Su notación de intervalo es negativa 2 a 2 dentro de un paréntesis y un paréntesis.$

7. $4x+6\leq 2$y$2x+1\geq −5$

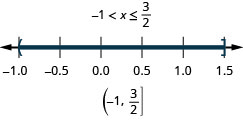
8. $4x−2\leq 4$y$7x−1>−8$

Contestar: $La solución es negativa 1 es menor que x que es menor o igual a tres mitades. Su gráfica tiene un círculo abierto en negativo 1 y un círculo cerrado en tres mitades con sombreado entre los círculos abierto y cerrado. Su notación de intervalo es negativa de 1 a tres mitades dentro de un paréntesis y un corchete.$

9. $2x−11<5$y$3x−8>−5$

10. $7x−8<6$y$5x+7>−3$

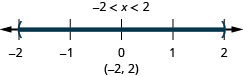
Contestar: $La solución es negativa 2 es menor que x que es menor que 2. Su gráfica tiene un círculo abierto en negativo 2 y un círculo abierto en 2 con sombreado entre los círculos abiertos. Su notación de intervalo es negativa 2 a 2 entre paréntesis.$

11. $4(2x−1)\leq 12$y$2(x+1)<4$

12. $5(3x−2)\leq 5$y$3(x+3)<3$

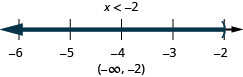
Contestar: $La solución es x es menor que negativa 2. Su gráfica tiene un círculo abierto en negativo 2 y está sombreada a la izquierda. Su notación de intervalo es de infinito negativo a negativo 2 entre paréntesis.$

13. $3(2x−3)>3$y$4(x+5)\geq 4$

14. $−3(x+4)<0$y$−1(3x−1)\leq 7$

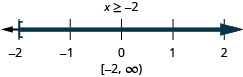
Contestar: $La solución es x es mayor o igual a negativo 2. Su gráfica tiene un círculo cerrado en negativo 2 y está sombreada a la derecha. Su notación de intervalo es negativa 2 a infinito dentro de un paréntesis y un paréntesis.$

15. $\frac{1}{2}(3x−4)\leq 1$y$\frac{1}{3}(x+6)\leq 4$

16. $\frac{3}{4}(x−8)\leq 3$y$\frac{1}{5}(x−5)\leq 3$

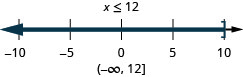
Contestar: $La solución es x es menor o igual a 12. Su gráfica tiene un círculo cerrado a las 12 y está sombreada a la izquierda. Su notación de intervalo es infinito negativo a 12 dentro de un paréntesis y un corchete.$

17. $5x−2\leq 3x+4$y$3x−4\geq 2x+1$

18. $\frac{3}{4}x−5\geq −2$y$−3(x+1)\geq 6$

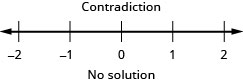
Contestar: $La solución es una contradicción. Entonces, no hay solución. Como resultado, no hay gráfica ni notación de línea numérica o intervalo.$

19. $\frac{2}{3}x−6\geq −4$y$−4(x+2)\geq 0$

20. $\frac{1}{2}(x−6)+2<−5$y$4−\frac{2}{3}x<6$

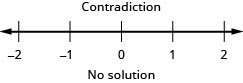
Contestar: $La solución es una contradicción. Entonces, no hay solución. Como resultado, no hay gráfica ni notación de línea numérica o intervalo.$

21. $−5\leq 4x−1<7$

22. $−3<2x−5\leq 1$

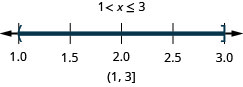
Contestar: $La solución es 1 es menor que x que es menor o igual a 3. Su gráfica tiene un círculo abierto en 1 y un círculo cerrado en 3 y está sombreado entre los círculos abierto y cerrado. Su notación de intervalo es de 1 a 3 dentro de un paréntesis y un corchete.$

23. $5<4x+1<9$

24. $−1<3x+2<8$

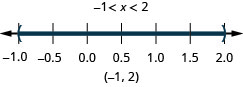
Contestar: $La solución es negativa 1 es menor que x que es menor que 2. Su gráfica tiene un círculo abierto en negativo 1 un círculo abierto en 2 y está sombreado entre ellos. Su notación de intervalo es negativa de 1 a 2 entre paréntesis.$

25. $−8<5x+2\leq −3$

26. $−6\leq 4x−2<−2$

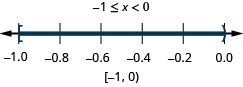
Contestar: $La solución es negativa 1 es menor o igual a x que es menor que o 0. Su gráfica tiene un círculo cerrado en negativo 1 y un círculo abierto en 0 y está sombreado entre los círculos cerrados y abiertos. Su notación de intervalo es negativa 1 a 0 dentro de un paréntesis y un paréntesis.$

Resolver desigualdades compuestas con “o”

En los siguientes ejercicios, resuelve cada desigualdad, grafica la solución en la recta numérica y escribe la solución en notación de intervalos.

27. $x\leq −2$o$x>3$

28. $x\leq −4$o$x>−3$

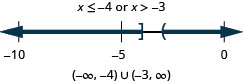
Contestar: $La solución es x es menor o igual a negativo 4 o x es mayor que negativo 3. El gráfico de las soluciones en una recta numérica tiene un círculo cerrado en negativo 4 y sombreado a la izquierda y un círculo abierto en negativo 3 con sombreado a la derecha. La notación de intervalo es la unión de infinito negativo a negativo 4 dentro de un paréntesis y un paréntesis y negativo 3 e infinito entre paréntesis.$

29. $x<2$o$x\geq 5$

30. $x<0$o$x\geq 4$

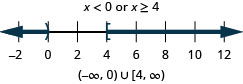
Contestar: $La solución es x es menor que 0 o x es mayor o igual a 2. El gráfico de las soluciones en una recta numérica tiene un círculo abierto a 0 y sombreado a la izquierda y un círculo cerrado en 4 con sombreado a la derecha. La notación de intervalo es la unión de infinito negativo a 0 entre paréntesis y 4 a infinito dentro de paréntesis y paréntesis.$

31. $2+3x\leq 4$o$5−2x\leq −1$

32. $4−3x\leq −2$o$2x−1\leq −5$

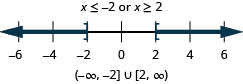
Contestar: $La solución es x es menor o igual a negativo 2 o x es mayor o igual a 2. El gráfico de las soluciones en una recta numérica tiene un círculo cerrado en negativo 2 y sombreado a la izquierda y un círculo cerrado en 2 con sombreado a la derecha. La notación de intervalo es la unión de infinito negativo a negativo 2 dentro de un paréntesis y un paréntesis y 2 a infinito dentro de un paréntesis y un paréntesis.$

33. $2(3x−1)<4$o$3x−5>1$

34. $3(2x−3)<−5$o
$4x−1>3$

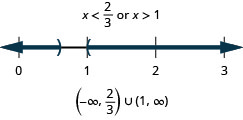
Contestar: $La solución es x es menor que dos tercios o x es mayor que 1. El gráfico de las soluciones en una recta numérica tiene un círculo abierto en dos tercios y sombreado a la izquierda y un círculo abierto en 1 con sombreado a la derecha. La notación de intervalo es la unión de infinito negativo a dos tercios entre paréntesis y 1 e infinito entre paréntesis.$

35. $\frac{3}{4}x−2>4$o$4(2−x)>0$

36. $\frac{2}{3}x−3>5$o$3(5−x)>6$

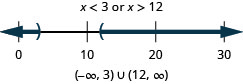
Contestar: $La solución es x es menor que 3 o x es mayor que 12. El gráfico de las soluciones en una recta numérica tiene un círculo abierto en 3 y sombreado a la izquierda y un círculo abierto a las 12 con sombreado a la derecha. La notación de intervalo es la unión de infinito negativo a 3 entre paréntesis y 12 e infinito entre paréntesis.$

37. $3x−2>4$o$5x−3\leq 7$

38. $2(x+3)\geq 0$o$3(x+4)\leq 6$

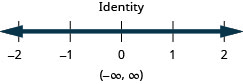
Contestar: $La solución es una identidad. Su solución en la recta numérica está sombreada para todos los valores. La solución en la notación de intervalos es infinito negativo a infinito entre paréntesis.$

39. $\frac{1}{2}x−3\leq 4$o$\frac{1}{3}(x−6)\geq −2$

40. $\frac{3}{4}x+2\leq −1$o$\frac{1}{2}(x+8)\geq −3$

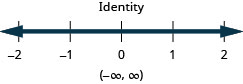
Contestar: $La solución es una identidad. Su solución en la recta numérica está sombreada para todos los valores. La solución en la notación de intervalos es infinito negativo a infinito entre paréntesis.$

Práctica mixta

En los siguientes ejercicios, resuelve cada desigualdad, grafica la solución en la recta numérica y escribe la solución en notación de intervalos.

41. $3x+7\leq 1$y$2x+3\geq −5$

42. $6(2x−1)>6$y$5(x+2)\geq 0$

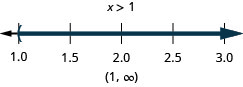
Contestar: $La solución es x es menor que 1. Su gráfica tiene un círculo abierto en negativo 1 está sombreado a la derecha. Su notación de intervalo es de 1 a infinito entre paréntesis.$

43. $4−7x\geq −3$o$5(x−3)+8>3$

44. $\frac{1}{2}x−5\leq 3$o$\frac{1}{4}(x−8)\geq −3$

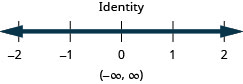
Contestar: $La solución es una identidad. Su solución en la recta numérica está sombreada para todos los valores. La solución en la notación de intervalos es infinito negativo a infinito entre paréntesis.$

45. $−5\leq 2x−1<7$

46. $\frac{1}{5}(x−5)+6<4$y$3−\frac{2}{3}x<5$

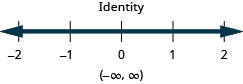
Contestar: $La desigualdad es una contradicción. Entonces, no hay solución. Como resultado, no hay gráfico en la línea numérica o notación de intervalo.$

47. $4x−2>6$o$3x−1\leq −2$

48. $6x−3\leq 1$y$5x−1>−6$

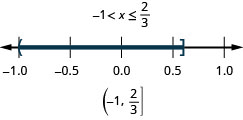
Contestar: $La solución es negativa 1 es menor que x que es menor o igual a dos tercios. Su gráfica tiene un círculo abierto en negativo 1 y un círculo cerrado en dos tercios y está sombreado entre los círculos abierto y cerrado. Su notación de intervalo es negativa de 1 a dos tercios dentro de un paréntesis y un paréntesis.$

49. $−2(3x−4)\leq 2$y$−4(x−1)<2$

50. $−5\leq 3x−2\leq 4$

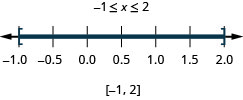
Contestar: $La solución es negativa 1 es menor o igual a x que es menor que 2. Su gráfica tiene un círculo cerrado en negativo 1 y un círculo cerrado en 2 y está sombreado entre los círculos cerrados. Su notación de intervalo es negativa de 1 a 4 entre paréntesis.$

Resolver aplicaciones con desigualdades compuestas

En los siguientes ejercicios, resuelve.

51. Penélope está jugando un juego de números con su hermana June. Penélope está pensando en un número y quiere que June lo adivine. Cinco más de tres veces su número está entre 2 y 32. Escribir una desigualdad compuesta que muestre el rango de números en los que Penélope podría estar pensando.

52. Gregory está pensando en un número y quiere que su hermana Lauren adivine el número. Su primera pista es que seis menos del doble de su número está entre cuatro y cuarenta y dos. Escribe una desigualdad compuesta que muestre el rango de números en los que Gregory podría estar pensando.

Contestar: $5\leq n\leq 24$

53. Andrew está creando una carrera de perros rectangular en su patio trasero. La longitud de la carrera para perros es de 18 pies. El perímetro de la carrera de perros debe ser de al menos 42 pies y no más de 72 pies. Use una desigualdad compuesta para encontrar el rango de valores para el ancho de la carrera de perros.

54. Elouise está creando un jardín rectangular en su patio trasero. La longitud del jardín es de 12 pies. El perímetro del jardín debe ser de al menos 36 pies y no más de 48 pies. Use una desigualdad compuesta para encontrar el rango de valores para el ancho del jardín.

Contestar: $6\leq w\leq 12$

Matemáticas cotidianas

55. Presión arterial La presión arterial de una persona se mide con dos números. La presión arterial sistólica mide la presión de la sangre en las arterias a medida que late el corazón. La presión arterial diastólica mide la presión mientras el corazón está en reposo.

ⓐ Deja x ser tu presión arterial sistólica. Investiga y luego escribe la desigualdad compuesta que te muestre lo que debería ser una presión arterial sistólica normal para alguien de tu edad.

ⓑ Deja y ser tu presión arterial diastólica. Investiga y luego escribe la desigualdad compuesta que te muestre lo que debería ser una presión arterial diastólica normal para alguien de tu edad.

56. El Índice de Masa Corporal (IMC) es una medida de la grasa corporal que se determina usando tu estatura y peso.

ⓐ Deja x ser tu IMC. Investigue y luego escriba la desigualdad compuesta para mostrar el rango de IMC para que se le considere peso normal.

ⓑ Investigue una calculadora de IMC y determine su IMC. ¿Es una solución a la desigualdad en la parte (a)?

Contestar: ⓐ las respuestas varían ⓑ las respuestas varían

Ejercicios de escritura

57. En sus propias palabras, explique la diferencia entre las propiedades de la igualdad y las propiedades de la desigualdad.

58. Explicar los pasos para resolver la desigualdad compuesta$2−7x\geq −5$ o$4(x−3)+7>3$.

Contestar: Las respuestas variarán.

Autocomprobación

ⓐ Después de completar los ejercicios, usa esta lista de verificación para evaluar tu dominio de los objetivos de esta sección.

$Esta tabla tiene cuatro columnas y cuatro filas. La primera fila es un encabezado y etiqueta a cada columna, “Puedo...”, “Con confianza”, “Con algo de ayuda” y “¡No-I don't get it!” En la fila 2, lo que puedo fue resolver desigualdades compuestas con “y”. En la fila 3, lo que puedo fue resolver desigualdades compuestas con “o”. En la fila 4, lo que puedo era resolver aplicaciones con desigualdades compuestas.$

ⓑ ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?