2.8E: Ejercicios

Última actualización
Guardar como PDF

Page ID: 112740

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

La práctica hace la perfección

Resolver ecuaciones de valor absoluto

En los siguientes ejercicios, resuelve.

1. a.$|x|=6$ b.$|y|=−3$ c.$|z|=0$

2. a.$ |x|=4$ b.$|y|=−5$ c.$|z|=0$

Contestar: a.$x=4,x=−4$ b. sin solución c.$z=0$

3. a.$|x|=7$ b.$|y|=−11$ c.$|z|=0$

4. a.$|x|=3$ b.$|y|=−1$ c.$|z|=0$

Contestar: a.$x=3,x=−3$ b. sin solución c.$z=0$

5. $|2x−3|−4=1$

6. $|4x−1|−3=0$

Contestar: $x=1, \,x=−\frac{1}{2}$

7. $|3x−4|+5=7$

8. $|4x+7|+2=5$

Contestar: $x=−1, \,x=−\frac{5}{2}$

9. $4|x−1|+2=10$

10. $3|x−4|+2=11$

Contestar: $x=7, \,x=1$

11. $3|4x−5|−4=11$

12. $3|x+2|−5=4$

Contestar: $x=1, \,x=−5$

13. $−2|x−3|+8=−4$

14. $−3|x−4|+4=−5$

Contestar: $x=7, \,x=1$

15. $|34x−3|+7=2$

16. $|35x−2|+5=2$

Contestar: no hay solución

17. $|12x+5|+4=1$

18. $|14x+3|+3=1$

Contestar: no hay solución

19. $|3x−2|=|2x−3|$

20. $|4x+3|=|2x+1|$

Contestar: $x=−1, \,x=−\frac{2}{3}$

21. $|6x−5|=|2x+3|$

22. $|6−x|=|3−2x|$

Contestar: $x=−3, \,x=3$

Resolver desigualdades de valor absoluto con “menos que”

En los siguientes ejercicios, resolver cada desigualdad. Grafica la solución y escribe la solución en notación de intervalos.

23. $|x|<5$

24. $|x|<1$

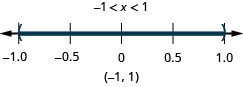
Contestar: $La solución es negativa 1 es menor que x que es menor que 1. La recta numérica muestra un círculo abierto en negativo 1, un círculo abierto en 1 y sombreado entre los círculos. La notación de intervalo es negativa 1 a 1 entre paréntesis.$

25. $|x|\leq 8$

26. $|x|\leq 3$

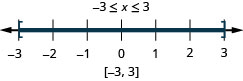
Contestar: $La solución es negativa 3 es menor o igual a x que es menor o igual a 3. La recta numérica muestra un círculo cerrado en negativo 3, un círculo cerrado en 3 y sombreado entre los círculos. La notación de intervalo es negativa 3 a 3 entre paréntesis.$

27. $|3x−3|\leq 6$

28. $|2x−5|\leq 3$

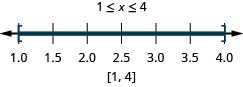
Contestar: $La solución es 1 es menor o igual a x que es menor o igual a 4. La recta numérica muestra un círculo cerrado en 1, un círculo cerrado en 4 y sombreado entre los círculos. La notación de intervalo es de 1 a 4 entre paréntesis.$

29. $|2x+3|+5<4$

30. $|3x−7|+3<1$

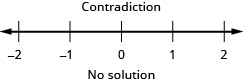
Contestar: $La solución es una contradicción. Entonces, no hay solución. Como resultado, no hay gráfica ni notación de línea numérica o intervalo.$

31. $|4x−3|<1$

32. $|6x−5|<7$

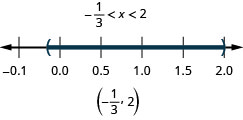
Contestar: $La solución es negativa un tercio es menor que x que es menor que 2. La recta numérica muestra un círculo abierto en la mitad negativa, un círculo abierto en 2 y sombreado entre los círculos. La notación de intervalo es negativa de un tercio a 2 entre paréntesis.$

33. $|x−4|\leq −1$

34. $|5x+1|\leq −2$

Contestar: $La solución es una contradicción. Entonces, no hay solución. Como resultado, no hay gráfica ni notación de línea numérica o intervalo.$

Resolver desigualdades de valor absoluto con “mayor que”

En los siguientes ejercicios, resolver cada desigualdad. Grafica la solución y escribe la solución en notación de intervalos.

35. $|x|>3$

36. $|x|>6$

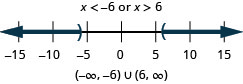
Contestar: $La solución es x es menor que negativo 6 o x es mayor que 6. La recta numérica muestra un círculo abierto en negativo 6 con sombreado a su izquierda y un círculo abierto en 6 con sombreado a su derecha. La notación de intervalo es la unión de infinito negativo a negativo 6 entre paréntesis y 6 a infinito entre paréntesis$

37. $|x|\geq 2$

38. $|x|\geq 5$

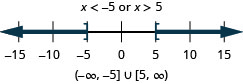
Contestar: $La solución es x es menor que negativo 5 o x es mayor que 5. La recta numérica muestra un círculo abierto en negativo 5 con sombreado a su izquierda y un círculo abierto a 5 con sombreado a su derecha. La notación de intervalo es la unión de infinito negativo a negativo 5 entre paréntesis y 5 a infinito entre paréntesis.$

39. $|3x−8|>−1$

40. $|x−5|>−2$

Contestar: $La solución es una identidad. Su solución en la recta numérica está sombreada para todos los valores. La solución en la notación de intervalos es infinito negativo a infinito entre paréntesis.$

41. $|3x−2|>4$

42. $|2x−1|>5$

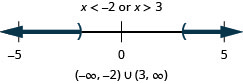
Contestar: $La solución es x es menor que negativo 2 o x es mayor que 3. La recta numérica muestra un círculo abierto en negativo 2 con sombreado a su izquierda y un círculo abierto en 3 con sombreado a su derecha. La notación de intervalo es la unión de infinito negativo a negativo 2 entre paréntesis y 3 a infinito entre paréntesis.$

43. $|x+3|\geq 5$

44. $|x−7|\geq 1$

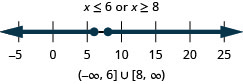
Contestar: $La solución es x es menor o igual a 6 o x es mayor o igual a 8. La recta numérica muestra un círculo cerrado a las 6 con sombreado a su izquierda y un círculo cerrado a las 8 con sombreado a su derecha. La notación de intervalo es la unión de infinito negativo a 6 entre paréntesis y un paréntesis y 8 a infinito dentro de un paréntesis y un paréntesis.$

45. $3|x|+4\geq 1$

46. $5|x|+6\geq 1$

Contestar: $La solución es una identidad. Su solución en la recta numérica está sombreada para todos los valores. La solución en la notación de intervalos es infinito negativo a infinito entre paréntesis.$

En los siguientes ejercicios, resuelve. Para cada desigualdad, también grafica la solución y escribe la solución en notación de intervalos.

47. $2|x+6|+4=8$

48. $|3x−4|\geq 2$

Contestar: $x=4,x=27$

49. $|6x−5|=|2x+3|$

50. $|4x−3|<5$

Contestar: $x=3,x=2$

51. $|2x−5|+2=3$

52. $|3x+1|−3=7$

Contestar: $x=3,x=−\frac{11}{3}$

53. $|7x+2|+8<4$

54. $5|2x−1|−3=7$

Contestar: $x=\frac{3}{2},x=−\frac{1}{2}$

55. $|x−7|>−3$

56. $|8−x|=|4−3x|$

Contestar: $La solución es una identidad. Su solución en la recta numérica está sombreada para todos los valores. La solución en la notación de intervalos es infinito negativo a infinito entre paréntesis.$

Resolver aplicaciones con valor absoluto

En los siguientes ejercicios, resuelve.

57. Una granja de pollos idealmente produce 200,000 huevos por día. Pero este total puede variar hasta en 25 mil huevos. ¿Cuál es la producción máxima y mínima esperada en la finca?

58. Un embotellador de jugo orgánico produce idealmente 215,000 botellas por día. Pero este total puede variar hasta en 7,500 botellas. ¿Cuál es la producción máxima y mínima esperada en la empresa embotelladora?

Contestar: La producción mínima a máxima esperada es de 207,500 a 2,225,000 botellas

59. Para asegurar el cumplimiento de la ley, Miguel rutinariamente rebasa en 0.5 gramos el peso de sus tortillas. Acaba de recibir un reporte que le decía que podría estar perdiendo hasta 100.000 dólares al año usando esta práctica. Ahora planea comprar equipo nuevo que garantice el grosor de la tortilla dentro de 0.005 pulgadas. Si el grosor ideal de la tortilla es de 0.04 pulgadas, ¿qué grosor de las tortillas se garantizará?

60. En Lilly Bakery, el peso ideal de una barra de pan es de 24 onzas. Por ley, el peso real puede variar del ideal en 1.5 onzas. ¿Qué rango de peso será aceptable para el inspector sin causar que la panadería sea multada?

Contestar: El peso aceptable es de 22.5 a 25.5 onzas.

Ejercicios de escritura

61. Escribir una descripción gráfica del valor absoluto de un número

62. En sus propias palabras, explique cómo resolver la desigualdad de valor absoluto,$|3x−2|\geq 4$.

Contestar: Las respuestas variarán.

Autocomprobación

a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

$Esta tabla tiene cuatro columnas y cinco filas. La primera fila es un encabezado y etiqueta a cada columna, “Puedo...”, “Con confianza”, “Con algo de ayuda” y “¡No-I don't get it!” En la fila 2, lo que puedo era resolver ecuaciones de valor absoluto. En la fila 3, lo que puedo fue resolver desigualdades de valor absoluto con “menos que”. En la fila 4, lo que puedo fue resolver desigualdades de valor absoluto con “mayor que”. En la fila 5, lo que puedo era resolver aplicaciones con valor absoluto.$

b. ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?

Search

Text Color

Text Size

Margin Size

Font Type