3.3E: Ejercicios

Última actualización
Guardar como PDF

Page ID: 112293

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

La práctica hace la perfección

Encuentra la Talud de una Línea

En los siguientes ejercicios, encuentra la pendiente de cada línea mostrada.

1.
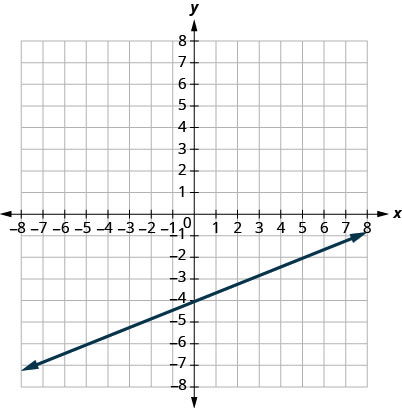
$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 8 a 8. El eje y va de negativo 8 a 8. La línea pasa por los puntos (0, negativo 4) y (5, negativo 2).$

Contestar: $m=\frac{2}{5}$

2.
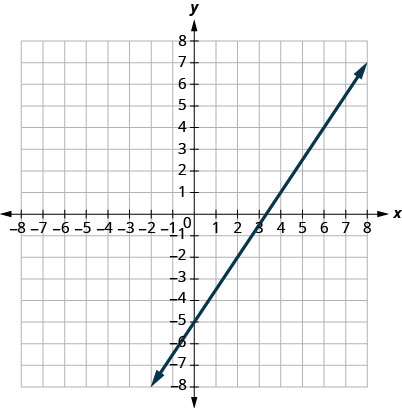
$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 8 a 8. El eje y va de negativo 8 a 8. La línea pasa por los puntos (0, negativo 5) y (2, negativo 2).$

3.
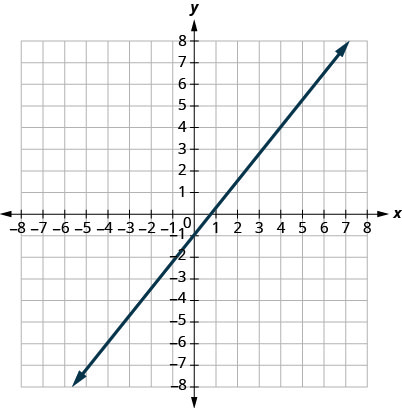
$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 8 a 8. El eje y va de negativo 8 a 8. La línea pasa por los puntos (0, negativo 1) y (4, 4).$

Contestar: $m=\frac{5}{4}$

4.
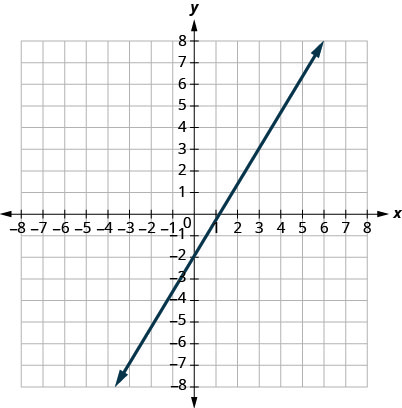
$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 8 a 8. El eje y va de negativo 8 a 8. La línea pasa por los puntos (0, negativo 2) y (3, 3).$

5.
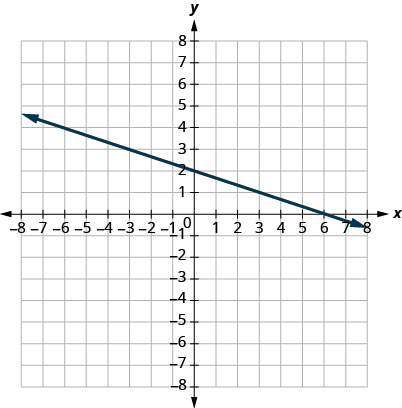
$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 8 a 8. El eje y va de negativo 8 a 8. La línea pasa por los puntos (0, 2) y (3, 1).$

Contestar: $m = -\frac{1}{3}$

6.
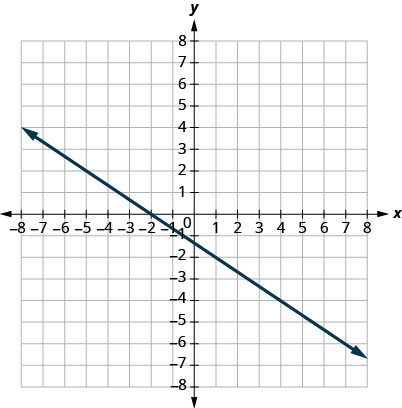
$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 8 a 8. El eje y va de negativo 8 a 8. La línea pasa por los puntos (0, negativo 1) y (3, negativo 3).$

7.
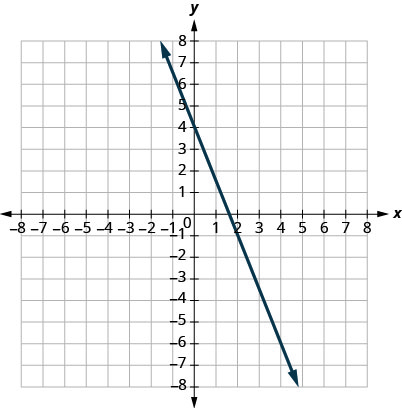
$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 8 a 8. El eje y va de negativo 8 a 8. La línea pasa por los puntos (0, 4) y (2, negativo 1).$

Contestar: $m = -\frac{5}{2}$

8.
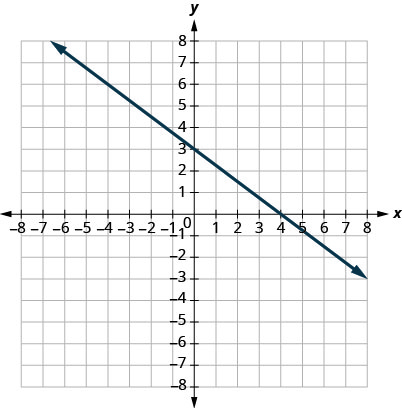
$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 8 a 8. El eje y va de negativo 8 a 8. La línea pasa por los puntos (0, 2) y (4, negativo 1).$

En los siguientes ejercicios, encuentra la pendiente de cada línea.

9. $y=3$

Contestar: $m = 0$

10. $y=−2$

11. $x=−5$

Contestar: undefined

12. $x=4$

En los siguientes ejercicios, usa la fórmula de pendiente para encontrar la pendiente de la línea entre cada par de puntos.

13. $(2,5),\;(4,0)$

Contestar: $m = -\frac{5}{2}$

14. $(3,6),\;(8,0)$

15. $(−3,3),\;(4,−5)$

Contestar: $m = -\frac{8}{7}$

16. $(−2,4),\;(3,−1)$

17. $(−1,−2),\;(2,5)$

Contestar: $m = \frac{7}{3}$

18. $(−2,−1),\;(6,5)$

19. $(4,−5),\;(1,−2)$

Contestar: $m = -1$

20. $(3,−6),\;(2,−2)$

Graficar una línea dado un punto y el talud

En los siguientes ejercicios, grafica cada línea con el punto y pendiente dados.

21. $(2,5)$;$m=−\frac{1}{3}$

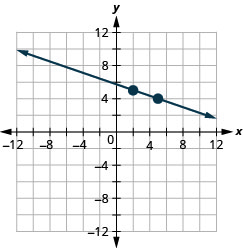
Contestar: $Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 12 a 12. El eje y va de negativo 12 a 12. La línea pasa por los puntos (2, 5) y (5, 4).$

22. $(1,4)$;$m=−\frac{1}{2}$

23. $(−1,−4)$;$m=\frac{4}{3}$

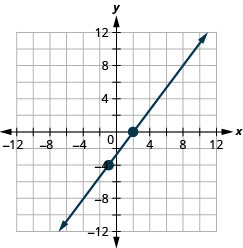
Contestar: $Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 12 a 12. El eje y va de negativo 12 a 12. La línea pasa por los puntos (negativo 1, negativo 4) y (2, 0).$

24. $(−3,−5)$;$m=\frac{3}{2}$

25. $y$-interceptar:$(0, 3)$;$m=−\frac{2}{5}$

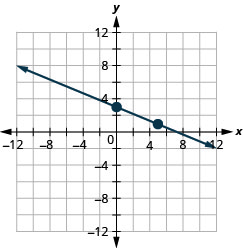
Contestar: $Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 12 a 12. El eje y va de negativo 12 a 12. La línea pasa por los puntos (0, 3) y (5, 1).$

26. $x$-interceptar:$(−2,0)$;$m=\frac{3}{4}$

27. $(−4,2)$;$m=4$

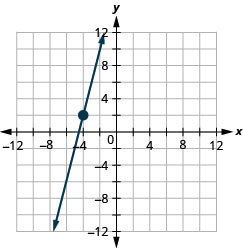
Contestar: $Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 12 a 12. El eje y va de negativo 12 a 12. La línea pasa por los puntos (negativo 4, 2) y (negativo 3, 6).$

28. $(1,5)$;$m=−3$

Graficar una línea usando su pendiente e intercepción

En los siguientes ejercicios, identificar la pendiente y -intercepción de cada línea.

29. $y=−7x+3$

Contestar: $m=−7$;$(0,3)$

30. $y=4x−10$

31. $3x+y=5$

Contestar: $m=−3$;$(0,5)$

32. $4x+y=8$

33. $6x+4y=12$

Contestar: $m=−\frac{3}{2}$;$(0,3)$

34. $8x+3y=12$

35. $5x−2y=6$

Contestar: $m=\frac{5}{2}$;$(0,−3)$

36. $7x−3y=9$

En los siguientes ejercicios, grafica la línea de cada ecuación usando su pendiente y -intercepción.

37. $y=3x−1$

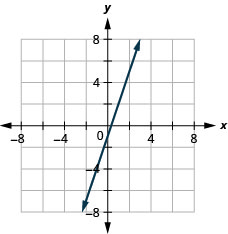
Contestar: $Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 10 a 10. El eje y va de negativo 10 a 10. La línea pasa por los puntos (0, negativo 1) y (1, 2).$

38. $y=2x−3$

39. $y=−x+3$

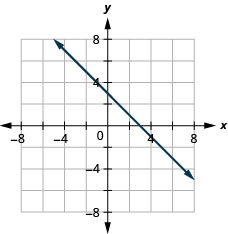
Contestar: $Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 10 a 10. El eje y va de negativo 10 a 10. La línea pasa por los puntos (0, 3) y (1, 2).$

40. $y=−x−4$

41. $y=−\frac{2}{5}x−3$

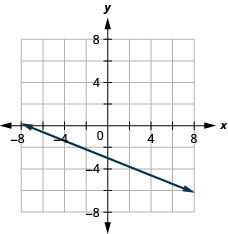
Contestar: $Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 10 a 10. El eje y va de negativo 10 a 10. La línea pasa por los puntos (0, negativo 3) y (5, negativo 5).$

42. $y=−\frac{3}{5}x+2$

43. $3x−2y=4$

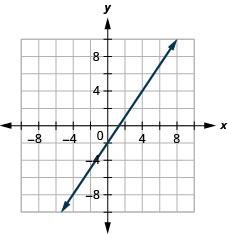
Contestar: $Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 10 a 10. El eje y va de negativo 10 a 10. La línea pasa por los puntos (0, negativo 2) y (2, 1).$

44. $3x−4y=8$

Elija el método más conveniente para graficar una línea

En los siguientes ejercicios, determine el método más conveniente para graficar cada línea.

45. $x=2$

Contestar: línea vertical

46. $y=5$

47. $y=−3x+4$

Contestar: pendiente-intercepción

48. $x−y=5$

49. $x−y=1$

Contestar: intercepta

50. $y=\frac{2}{3}x−1$

51. $3x−2y=−12$

Contestar: intercepta

52. $2x−5y=−10$

Graficar e interpretar aplicaciones de pendiente: interceptar

53. La ecuación$P=31+1.75w$ modela la relación entre el monto del pago mensual de la factura de agua de Tuyet$P$, en dólares, y el número de unidades de agua,$w$, utilizadas.

a. encontrar el pago de Tuyet por un mes cuando se utilizan$0$ unidades de agua.

b. encontrar el pago de Tuyet por un mes cuando se utilizan$12$ unidades de agua.

c. Interpretar la pendiente e$P$ -intercepción de la ecuación.

d. Grafica la ecuación.

Contestar

a.$$31$
b.$$52$
c. La pendiente,$1.75$, significa que el pago,$P$, aumenta$$1.75$ cuando el número de unidades de agua utilizadas,$w$, aumenta en$1$. El$P$ -intercepto significa que cuando el número de unidades de agua que Tuyet utilizó es$0$, el pago es$$31$.
d.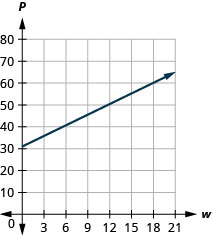

$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de 1 negativo a 21. El eje y va de 1 negativo a 80. La línea pasa por los puntos (0, 31) y (12, 52).$

54. La ecuación$P=28+2.54w$ modela la relación entre el monto del pago mensual de la factura de agua de Randy$P$, en dólares, y el número de unidades de agua,$w$, utilizadas.

a. encontrar el pago de un mes cuando Randy utilizó$0$ unidades de agua.

b. encontrar el pago por un mes cuando Randy utilizó$15$ unidades de agua.

c. Interpretar la pendiente e$P$ -intercepción de la ecuación.

d. Grafica la ecuación.

55. Bruce conduce su auto para su trabajo. La ecuación$R=0.575m+42$ modela la relación entre el monto en dólares$R$,, que se le reembolsa y el número de millas$m$,, conduce en un día.

a. Encuentra la cantidad que Bruce es reembolsado en un día en el que conduce$0$ millas.

b. encontrar la cantidad que Bruce es reembolsado en un día en que conduce$220$ millas.

c. Interpretar la pendiente e$R$ -intercepción de la ecuación.

d. Grafica la ecuación.

Contestar

a.$$42$
b.$$168.50$
c. La pendiente,$0.575$ significa que la cantidad que se le reembolsa,$R$, aumenta$$0.575$ cuando el número de millas recorridas,$m$, aumenta en$1$. El$R$ -intercepto significa que cuando el número de millas conducidas es$0$, el monto reembolsado es$$42$.
d.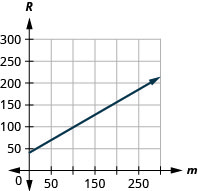

$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 50 a 250. El eje y va de negativo 50 a 300. La línea pasa por los puntos (0, 42) y (220, 168.5).$

56. Janelle planea rentar un auto mientras está de vacaciones. La ecuación$C=0.32m+15$ modela la relación entre el costo en dólares$C$,, por día y el número de millas,$m$, ella conduce en un día.

a. Encuentra el costo si Janelle conduce el auto$0$ millas un día.

b. Encuentra el costo en un día en que Janelle conduce$400$ millas del auto.

c. Interpretar la pendiente e$C$ -intercepción de la ecuación.

d. Grafica la ecuación.

57. Cherie trabaja en retail y su salario semanal incluye comisión por la cantidad que vende. La ecuación$S=400+0.15c$ modela la relación entre su salario semanal$S$,, en dólares y el monto de sus ventas,$c$, en dólares.

a. encontrar el salario de Cherie para una semana cuando sus ventas fueron$$0$.

b. encontrar el salario de Cherie para una semana cuando sus ventas fueron$$3,600$.

c. Interpretar la pendiente e$S$ -intercepción de la ecuación.

d. Grafica la ecuación.

Contestar

a.$$400$
b.$$940$
c. La pendiente,$0.15$, significa que el salario de Cherie, S, aumenta$$0.15$ por cada$$1$ incremento en sus ventas. El$S$ -intercepto significa que cuando sus ventas son$$0$, su salario lo es$$400$.
d.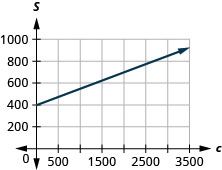

$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de 500 negativos a 3500. El eje y va de 200 negativos a 1000. La línea pasa por los puntos (0, 400) y (3600, 940).$

58. El salario semanal de Patel incluye un sueldo base más una comisión por sus ventas. La ecuación$S=750+0.09c$ modela la relación entre su salario semanal$S$,, en dólares y el monto de sus ventas,$c$, en dólares.

a. encontrar el salario de Patel para una semana cuando sus ventas fueron$0$.

b. encontrar el salario de Patel para una semana cuando sus ventas fueron$18,540$.

c. Interpretar la pendiente e$S$ -intercepción de la ecuación.

d. Grafica la ecuación.

59. Costa está planeando un banquete de almuerzo. La ecuación$C=450+28g$ modela la relación entre el costo en dólares,$C$, del banquete y el número de invitados,$g$.

a. Encuentra el costo si el número de invitados es$40$.

b. Averiguar el costo si el número de invitados es$80$.

c. Interpretar la pendiente e$C$ -intercepción de la ecuación.

d. Grafica la ecuación.

Contestar

a.$$1570$
b.$$5690$
c. La pendiente da el costo por huésped. La pendiente,$28$, significa que el costo,$C$, aumenta$$28$ cuando el número de invitados aumenta en$1$. El$C$ -intercepto significa que si el número de invitados fuera$0$, el costo sería$$450$.
d.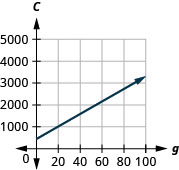

$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de 20 a 100 negativos. El eje y va de negativo 1000 a 7000. La línea pasa por los puntos (0, 450) y (40, 1570).$

60. Margie está planeando una cena banquete. La ecuación$C=750+42g$ modela la relación entre el costo en dólares,$C$, del banquete y el número de invitados,$g$.

a. Encuentra el costo si el número de invitados es$50$.

b. Averiguar el costo si el número de invitados es$100$.

c. Interpretar la pendiente e$C$ -intercepción de la ecuación.

d. Grafica la ecuación.

Utilizar pendientes para identificar líneas paralelas y perpendiculares

En los siguientes ejercicios, use pendientes e$y$ intercepciones para determinar si las líneas son paralelas, perpendiculares o ninguna.

61. $y=\frac{3}{4}x−3$;$3x−4y=−2$

Contestar: paralelo

62. $3x−4y=−2$;$y=\frac{3}{4}x−3$

63. $2x−4y=6$;$x−2y=3$

Contestar: ni

64. $8x+6y=6$;$12x+9y=12$

65. $x=5$;$x=−6$

Contestar: paralelo

66. $x=−3$;$x=−2$

67. $4x−2y=5$;$3x+6y=8$

Contestar: perpendicular

68. $8x−2y=7$;$3x+12y=9$

69. $3x−6y=12$;$6x−3y=3$

Contestar: ni

70. $9x−5y=4$;$5x+9y=−1$

71. $7x−4y=8$;$4x+7y=14$

Contestar: perpendicular

72. $5x−2y=11$;$5x−y=7$

73. $3x−2y=8$;$2x+3y=6$

Contestar: perpendicular

74. $2x+3y=5$;$3x−2y=7$

75. $3x−2y=1$;$2x−3y=2$

Contestar: ni

76. $2x+4y=3$;$6x+3y=2$

77. $y=2$;$y=6$

Contestar: paralelo

78. $y=−1$;$y=2$

Ejercicios de escritura

79. ¿En qué se$m=12$ diferencia la gráfica de una línea con pendiente de la gráfica de una línea con pendiente$m=2$?

Contestar: Las respuestas variarán.

80. ¿Por qué la pendiente de una línea vertical es “indefinida”?

81. Explica cómo puedes graficar una línea dado un punto y su pendiente.

Contestar: Las respuestas variarán.

82. Explica con tus propias palabras cómo decidir qué método usar para graficar una línea.

Autocomprobación

a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

$Esta tabla tiene 7 filas y 4 columnas. La primera fila es una fila de encabezado y etiqueta cada columna. El encabezado de la primera columna es “Puedo...”, el segundo es “Con confianza”, el tercero es “Con algo de ayuda”, y el cuarto es “No, no lo consigo”. Debajo de la primera columna están las frases “encontrar la pendiente de una línea”, “graficar una línea dado un punto y la pendiente”, “graficar una línea usando su pendiente e interceptar”, “elegir el método más conveniente para graficar una línea”, “graficar e interpretar aplicaciones de pendiente-intercepción”, y “usar pendientes para identificar paralelas y líneas perpendiculares”. Las otras columnas se dejan en blanco para que el alumno pueda indicar su nivel de dominio para cada tema.$

b. Después de revisar esta lista de verificación, ¿qué harás para tener confianza en todos los objetivos?

Search

Text Color

Text Size

Margin Size

Font Type