3.3: Pendiente de una línea

Última actualización
Guardar como PDF

Page ID: 112280

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Al final de esta sección, podrás:

Encuentra la pendiente de una línea
Graficar una línea dada un punto y la pendiente
Graficar una línea usando su pendiente e intercepción
Elija el método más conveniente para graficar una línea
Graficar e interpretar aplicaciones de pendiente-intercepción
Usar pendientes para identificar líneas paralelas y perpendiculares

Antes de comenzar, toma este cuestionario de preparación.

Simplificar:$\frac{(1–4)}{(8−2)}$.
Si te perdiste este problema, revisa [enlace].
Dividir:$\frac{0}{4}$,$\frac{4}{0}$.
Si te perdiste este problema, revisa [enlace].
Simplificar:$\frac{15}{-3}$,$\frac{-15}{3}$,$\frac{-15}{-3}$.
Si te perdiste este problema, revisa [enlace].

Encuentra la Talud de una Línea

Cuando graficas ecuaciones lineales, puedes notar que algunas líneas se inclinan hacia arriba a medida que van de izquierda a derecha y algunas líneas se inclinan hacia abajo. Algunas líneas son muy empinadas y algunas líneas son más planas.

En matemáticas, la medida de la inclinación de una línea se llama pendiente de la línea.

El concepto de talud tiene muchas aplicaciones en el mundo real. En construcción la inclinación de un techo, la inclinación de las tuberías de plomería, y la inclinación de las escaleras son todas aplicaciones de pendiente. y a medida que esquias o trotas cuesta abajo, definitivamente experimentas pendiente.

Podemos asignar un valor numérico a la pendiente de una línea encontrando la relación entre la subida y la carrera. La subida es la cantidad que cambia la distancia vertical mientras que la carrera mide el cambio horizontal, como se muestra en esta ilustración. La pendiente es una tasa de cambio. Ver Figura.

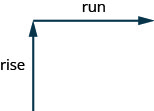
Esta figura tiene un diagrama de dos flechas. La primera flecha es vertical y apuntada hacia arriba y etiquetada como “subir”. La segunda flecha comienza al final de la primera. La segunda flecha es horizontal y puntiaguda hacia la derecha y etiquetada como “correr”. — Figura$\PageIndex{1}$.

PENDIENTE DE UNA LÍNEA

La pendiente de una línea es$m=\frac{\text{rise}}{\text{run}}$.

La subida mide el cambio vertical y la corrida mide el cambio horizontal.

Para encontrar la pendiente de una línea, localizamos dos puntos en la línea cuyas coordenadas son números enteros. Después dibujamos un triángulo rectángulo donde los dos puntos son vértices y un lado es horizontal y un lado es vertical.

Para encontrar la pendiente de la línea, medimos la distancia a lo largo de los lados vertical y horizontal del triángulo. La distancia vertical se llama subida y la distancia horizontal se llama carrera,

ENCUENTRA LA PENDIENTE DE UNA LÍNEA A PARTIR$m=\frac{\text{rise}}{\text{run}}$

Localice dos puntos en la línea cuyas coordenadas sean números enteros.
Comenzando con un punto, esboza un triángulo rectángulo, yendo del primer punto al segundo punto.
Cuenta la subida y la carrera en las piernas del triángulo.
Toma la relación de subida para correr para encontrar la pendiente:$m=\frac{\text{rise}}{\text{run}}$.

Ejemplo$\PageIndex{1}$

Encuentra la pendiente de la línea que se muestra.

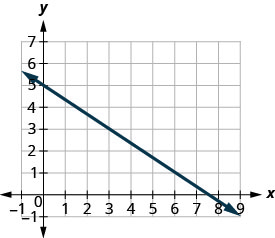
$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 1 a 9. El eje y va de negativo 1 a 7. La línea pasa por los puntos (0, 5), (3, 3) y (6, 1).$

Responder

Localice dos puntos en la gráfica cuyas coordenadas sean números enteros.	$(0,5)$y$(3,3)$
A partir de$(0,5)$, esboce un triángulo rectángulo $(3,3)$ como se muestra en esta gráfica.	$.$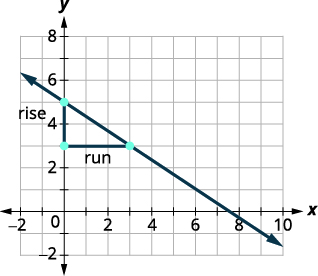
Cuenta la subida— ya que baja, es negativo.	El ascenso es$−2$.
Cuenta la carrera.	La carrera es 3.
Utilice la fórmula de pendiente.	$m=\frac{\text{rise}}{\text{run}}$
Sustituir los valores de la subida y corrida.	$m=−23$
Simplificar.	$m=−23$
	La pendiente de la línea es$−23$.
	Entonces y disminuye en 2 unidades a medida que x aumenta en 3 unidades.

Ejemplo$\PageIndex{2}$

Encuentra la pendiente de la línea que se muestra.

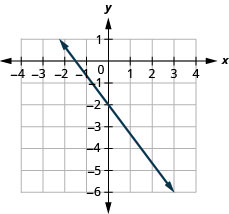
$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 1 a 5. El eje y va de 6 a 1 negativo. La línea pasa por los puntos (0, negativo 2) y (3, negativo 6).$

Responder: $-\frac{4}{3}$

Ejemplo$\PageIndex{3}$

Encuentra la pendiente de la línea que se muestra.

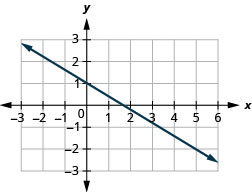
$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de 3 a 6 negativos. El eje y va de negativo 3 a 2. La línea pasa por los puntos (0, 1) y (5, negativo 2).$

Responder: $-\frac{3}{5}$

¿Cómo encontramos la pendiente de las líneas horizontales y verticales? Para encontrar la pendiente de la línea horizontal,$y=4$, podríamos graficar la línea, encontrar dos puntos en ella, y contar la subida y la carrera. Veamos qué pasa cuando hacemos esto, como se muestra en la gráfica a continuación.

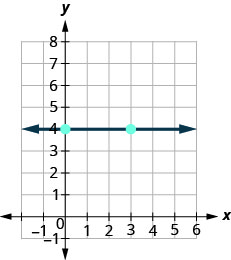
$A continuación, la figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 1 a 6. El eje y va de negativo 1 a 8. La línea pasa por los puntos (0, 4) y (3, 4). ¿Cuál es la subida? El ascenso es 0. ¿Cuál es la carrera? La carrera es 3. ¿Cuál es la pendiente? m es igual a aumento dividido por carrera. m es igual a 0 dividido por 3. m es igual a 0. La pendiente de la línea horizontal y es igual a 4 es 0.$

$ \begin{array} {ll} {\text{What is the rise?}} &{\text{The rise is }0.} \\ {\text{What is the run?}} &{\text{The run is }3.} \\ {\text{What is the slope?}} &{m=\frac{\text{rise}}{\text{run}}} \\ {} &{m=\frac{0}{3}} \\ {} &{m=0} \\{}&{\text{The slope of the horizontal line } y=4 \text{ is }0.} \\ \end{array} \nonumber$

Consideremos también una línea vertical, la línea$x=3$, como se muestra en la gráfica.

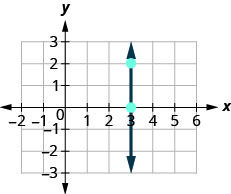
$A continuación, la figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 2 a 6. El eje y va de negativo 3 a 3. La línea pasa por los puntos (3, 0) y (3, 2). ¿Cuál es la subida? El ascenso es de 2. ¿Cuál es la carrera? La carrera es 0. ¿Cuál es la pendiente? m es igual a aumento dividido por carrera. m es igual a 2 dividido por 0.$

La pendiente es indefinida ya que la división por cero es indefinida. Entonces decimos que la pendiente de la línea vertical$x=3$ es indefinida.

Todas las líneas horizontales tienen pendiente 0. Cuando las coordenadas y son las mismas, la subida es 0.

La pendiente de cualquier línea vertical es indefinida. Cuando las coordenadas x de una línea son todas iguales, la ejecución es 0.

Talud de una línea horizontal y vertical

La pendiente de una línea horizontal,$y=b$, es 0.

La pendiente de una línea vertical,$x=a$, es indefinida.

Ejemplo$\PageIndex{4}$

Encuentra la pendiente de cada línea: ⓐ$x=8$ ⓑ $y=−5$.

Responder: ⓐ$x=8$
Esta es una línea vertical. Su pendiente es indefinida.
ⓑ$y=−5$
Esta es una línea horizontal. Tiene pendiente 0.

Ejemplo$\PageIndex{5}$

Encuentra la pendiente de la línea:$x=−4$.

Responder: undefined

Ejemplo$\PageIndex{6}$

Encuentra la pendiente de la línea:$y=7$.

Responder: 0

GUÍA RÁPIDA DE LAS PISTAS DE

$En la imagen se muestran cuatro flechas. La primera flecha está inclinada y apuntando hacia arriba y hacia la derecha y está etiquetada como “positiva”. La segunda flecha está inclinada y apuntando hacia abajo y hacia la derecha y etiquetada como “negativa”. La tercera flecha es horizontal y está etiquetada como “cero”. La cuarta flecha es vertical y está etiquetada como “indefinida”.$

A veces necesitaremos encontrar la pendiente de una línea entre dos puntos cuando no tenemos una gráfica para contar la subida y la carrera. Podríamos trazar los puntos en papel de rejilla, luego contar la subida y la carrera, pero como veremos, hay una manera de encontrar la pendiente sin graficar. Antes de llegar a ella, necesitamos introducir alguna notación algebraica.

Hemos visto que un par ordenado (x, y) (x, y) da las coordenadas de un punto. Pero cuando trabajamos con pendientes, utilizamos dos puntos. ¿Cómo se puede usar el mismo símbolo (x, y) (x, y) para representar dos puntos diferentes? Los matemáticos utilizan subíndices para distinguir los puntos.

$ \begin{array} {ll} {(x_1, y_1)} &{\text{read “} x \text{ sub } 1, \space y \text{ sub } 1 \text{”}} \\ {(x_2, y_2)} &{\text{read “} x \text{ sub } 2, \space y \text{ sub } 2 \text{”}} \\ \end{array} \nonumber$

Utilizaremos$(x_1,y_1)$ para identificar el primer punto y$(x_2,y_2)$ para identificar el segundo punto.

Si tuviéramos más de dos puntos, podríamos usar$(x_3,y_3)$,$(x_4,y_4)$, y así sucesivamente.

Veamos cómo la subida y la carrera se relacionan con las coordenadas de los dos puntos al echar otro vistazo a la pendiente de la línea entre los puntos$(2,3)$ y$(7,6)$, como se muestra en esta gráfica.

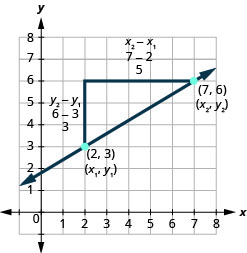
$La figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 1 a 7. El eje y va de negativo 1 a 7. La línea pasa por los puntos (2, 3) y (7, 6). Se dibuja un triángulo rectángulo conectando los tres puntos (2, 3), (2, 6) y (7, 6). El punto (2, 3) está etiquetado (x 1, y 1). El punto (7, 6) está etiquetado (x 2, y 2). El lado vertical del triángulo tiene etiquetas y 2 menos y 1, 6 menos 3, y 3. El lado horizontal del triángulo tiene etiquetas x 2 menos x 1, 7 menos 2 y 5.$

\( \begin{array} {ll} {\text{Since we have two points, we will use subscript notation.}} &{ \begin{pmatrix} x_1, & y_1 \\ 2 & 3 \end{pmatrix} \begin{pmatrix} x_2, & y_2 \\ 6 & 6 \end{pmatrix}} \\ {} &{m=\frac{\text{rise}}{\text{run}}} \\ {\text{On the graph, we counted the rise of 3 and the run of 5.}} &{m=\frac{3}{5}} \\ {\text{Notice that the rise of 3 can be found by subtracting the}} &{} \\ {y\text{-coordinates, 6 and 3, and the run of 5 can be found by}} &{} \\ {\text{subtracting the x-coordinates 7 and 2.}} &{} \\ {\text{We rewrite the rise and run by putting in the coordinates.}} &{m=\frac{6-3}{7-2}} \\ {} &{} \\ {\text{But 6 is } y_2 \text{, the y-coordinate of the second point and 3 is }y_1 \text{, the y-coordinate}} &{} \\ {\text{of the first point. So we can rewrite the slope using subscript notation.}} &{m=\frac{y_2-y_1}{7-2}} \\ {\text{Also 7 is the x-coordinate of the second point and 2 is the x-coordinate}} &{} \\ {\text{of the first point. So again we rewrite the slope using subscript notation.}} &{m=\frac{y_2-y_1}{x_2-x_1}} \\ \end{array} \nonumber\)

Hemos demostrado que en realidad$m=\frac{y_2−y_1}{x_2−x_1}$ es otra versión de$m=\frac{\text{rise}}{\text{run}}$. Podemos usar esta fórmula para encontrar la pendiente de una línea cuando tenemos dos puntos en la línea.

Talud de una línea entre dos puntos

La pendiente de la línea entre dos puntos$(x_1,y_1)$ y$(x_2,y_2)$ es:

$m=\frac{y_2−y_1}{x_2−x_1}$.

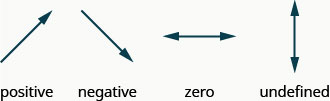
La pendiente es:

\[y\text{ of the second point minus }y\text{ of the first point} \nonumber\]\[\text{over} \nonumber\]\[x\text{ of the second point minus }x\text{ of the first point} \nonumber\]

Ejemplo$\PageIndex{7}$

Utilice la fórmula de pendiente para encontrar la pendiente de la línea a través de los puntos$(−2,−3)$ and $(-7,4)$.

Responder

$ \begin{array} {ll} {\text{We’ll call (−2,−3) point #1and (−7,4) point #2.}} &{ \begin{pmatrix} x_1, & y_1 \\ -2 & -3 \end{pmatrix} \begin{pmatrix} x_2, & y_2 \\ -7 & 4 \end{pmatrix}} \\ {\text{Use the slope formula.}} &{m=\frac{y_2-y_1}{x_2-x_1}} \\ {\text{Substitute the values.}} &{} \\ {\text{y of the second point minus y of the first point}} &{} \\ {\text{x of the second point minus x of the first point}} &{m=\frac{4-(-3)}{-7-(-2)}} \\{\text{Simplify}}&{m=\frac{7}{-5}} \\ {} &{m=\frac{-7}{5}} \\ \end{array} \nonumber$

Verifiquemos esta pendiente en la gráfica que se muestra.

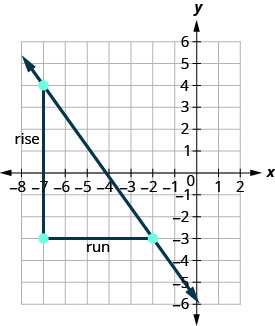
$La figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 8 a 2. El eje y va de 6 a 6 negativos. La línea pasa por los puntos (negativo 7, 4) y (negativo 2, negativo 3). Se dibuja un triángulo rectángulo conectando los tres puntos (negativo 7, 4), (negativo 7, negativo 3) y (negativo 2, negativo 3). El lado vertical del triángulo está etiquetado como “subida”. El lado horizontal del triángulo está etiquetado como “correr”.$

\[m=\frac{\text{rise}}{\text{run}} \nonumber\]\[m=\frac{7}{−5} \nonumber\]\[m=\frac{−7}{5} \nonumber\]

Utilice la fórmula de pendiente para encontrar la pendiente de la línea a través del par de puntos:$(−3,4)$ y$(2,−1)$.

Responder: $-1$

Ejemplo$\PageIndex{9}$

Utilice la fórmula de pendiente para encontrar la pendiente de la línea a través del par de puntos:$(−2,6)$ y$(−3,−4)$.

Responder: 10

Graficar una línea dado un punto y el talud

Hasta ahora, en este capítulo, hemos graficado líneas trazando puntos, usando intercepciones y reconociendo líneas horizontales y verticales.

También podemos graficar una línea cuando conocemos un punto y la pendiente de la línea. Comenzaremos trazando el punto y luego usaremos la definición de pendiente para dibujar la gráfica de la línea.

Ejemplo$\PageIndex{10}$: How to graph a Line Given a Point and the Slope

Grafica la línea que pasa por el punto$(1,−1)$ cuya pendiente es$m=\frac{3}{4}$.

Responder

$El paso 1 es trazar el punto dado. Parcela (1, negativo 1). A continuación, la figura muestra la gráfica de un punto en el plano de la coordenada x y. El eje x va de negativo 2 a 6. El eje y va de negativo 2 a 4. El punto (1, negativo 1) se traza y se etiqueta con sus coordenadas.$ $El paso 2 consiste en utilizar la fórmula de pendiente m es igual a subida dividida por carrera para identificar la subida y la carrera. Identificar la subida y la carrera. m es igual a 3 dividido por 4. La subida dividida por corrida equivale a 3 dividido por 4. La subida es igual a 3. Ejecutar es igual a 4.$ $El paso 3 es comenzar en el punto dado y contar la subida y correr para marcar el segundo punto. Empezar en (1, negativo 1) y contar la subida y la carrera. Hasta 3 unidades, derecha 4 unidades. A continuación, la figura muestra la gráfica de tres puntos conectados por dos segmentos de línea recta en el plano de la coordenada x y. El eje x va de negativo 2 a 6. El eje y va de negativo 2 a 4. Se trazan los puntos (1, negativo 1), (1, 2) y (5, 2). Un segmento de línea vertical conecta (1, negativo 1) a (1, 2) y está etiquetado como 3. Un segmento de línea horizontal conecta (1, 2) a (5, 2) y está etiquetado como 4.$ $El paso 4 es conectar los puntos con una línea. Conecta los dos puntos con una línea. A continuación, la figura muestra la gráfica de una línea recta, tres puntos y dos segmentos de línea en el plano de la coordenada x y. El eje x va de negativo 2 a 6. El eje y va de negativo 2 a 4. Se trazan los puntos (1, negativo 1), (1, 2) y (5, 2). Un segmento de línea vertical conecta (1, negativo 1) a (1, 2). Un segmento de línea horizontal conecta (1, 2) a (5, 2) y está etiquetado como 4. Se dibuja una línea recta a través de los puntos (1, negativo 1) y (5, 2) con flechas en ambos extremos.$

Puedes verificar tu trabajo encontrando un tercer punto. Ya que la pendiente es$m=34$, también se puede escribir como$m=\frac{−3}{−4}$ (¡negativo dividido por negativo es positivo!). Volver a$(1,−1)$ y contar la subida,$−3$, y la carrera,$−4$.

Ejemplo$\PageIndex{11}$

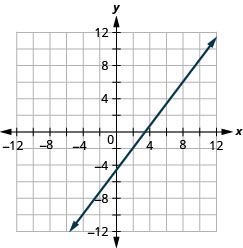
Grafica la línea que pasa por el punto$(2,−2$ con la pendiente$m=\frac{4}{3}$.

Responder: $Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 12 a 12. El eje y va de negativo 12 a 12. La línea pasa por los puntos (2, negativo 2) y (5, 2).$

Ejemplo$\PageIndex{12}$

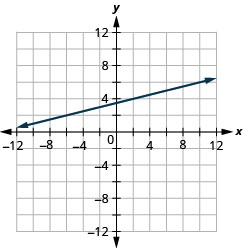
Grafica la línea que pasa por el punto$(−2,3)$ with the slope $m=\frac{1}{4}$.

Responder: $Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 12 a 12. El eje y va de negativo 12 a 12. La línea pasa por los puntos (negativo 2, 3) y (2, 4).$

GRÁFICA UNA LÍNEA DADA UN PUNTO Y LA T

Trazar el punto dado.
Utilice la fórmula de pendiente$m=\frac{\text{rise}}{\text{run}}$ para identificar la subida y la carrera.
Comenzando en el punto dado, cuente la subida y corra para marcar el segundo punto.
Conecta los puntos con una línea.

Graficar una línea usando su pendiente e intercepción

Hemos graficado ecuaciones lineales trazando puntos, usando intercepciones, reconociendo líneas horizontales y verticales, y usando un punto y la pendiente de la línea. Una vez que veamos cómo se relacionan una ecuación en forma pendiente-intercepción y su gráfica, tendremos un método más que podemos usar para graficar líneas.

Ver Figura. Veamos la gráfica de la ecuación$y=12x+3$ y encontremos su pendiente y -intercepción.

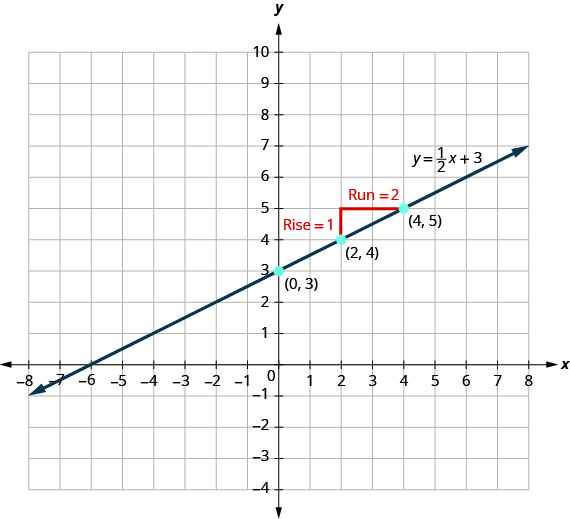
La figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 10 a 10. El eje y va de negativo 10 a 10. La línea pasa por los puntos (0, 3), (2, 4) y (4, 5). Se dibuja un triángulo rectángulo conectando los tres puntos (2, 4), (2, 5) y (4, 5). El lado vertical del triángulo está etiquetado como “La subida es igual a 1”. El lado horizontal del triángulo está etiquetado como “Ejecutar es igual a 2”. La línea está etiquetada y es igual a 1 dividido por 2 x más 3. — Figura$\PageIndex{2}$

Las líneas rojas en la gráfica nos muestran que la subida es 1 y la corrida es 2. Sustituyendo en la fórmula de pendiente:

\[m=\frac{\text{rise}}{\text{run}} \nonumber\]\[m=\frac{1}{2} \nonumber\]

La intercepción y es$(0,3)$.

Mira la ecuación de esta línea.

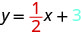
$La figura muestra la ecuación y es igual a 1 dividido por 2 x más 3. El 1 dividido por 2 se enfatiza en rojo. El 3 se enfatiza en azul.$

Mirar la pendiente y -interceptar.

$Pendiente m es igual a 1 dividido por 2 e intercepción y (0, 3). El 1 dividido por 2 se enfatiza en rojo. El 3 se enfatiza en azul.$

Cuando se resuelve una ecuación lineal para y, el coeficiente del término x es la pendiente y el término constante es la coordenada y de la intercepción y. Decimos que la ecuación$y=12x+3$ está en forma pendiente-intercepción. A veces la forma pendiente-intercepción se llama la “forma y”.

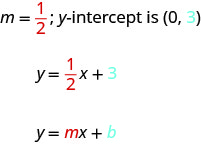
$m es igual a 1 dividido por 2; y-intercept es (0, 3). y es igual a 1 dividido por 2 x más 3. y es igual a m x más b. La m y 1 dividida por 2 se enfatizan en rojo. El b y el 3 se enfatizan en azul.$

FORMA DE INTERCEPCIÓN DE PENDIENTE DE UNA ECUACIÓN DE

La forma pendiente-intercepción de una ecuación de una línea con pendiente m e intercepción y,$(0,b)$ es$y=mx+b$.

Practicemos encontrar los valores de la pendiente y -interceptar a partir de la ecuación de una línea.

Ejemplo$\PageIndex{13}$

Identificar la pendiente y -intercepción de la línea a partir de la ecuación:

ⓐ$y=−\frac{4}{7}x−2$ ⓑ$x+3y=9$

Responder

ⓐ Comparamos nuestra ecuación con la forma pendiente-intercepción de la ecuación.

Escriba la forma pendiente-intercepción de la ecuación de la línea.	$.$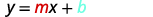
Escribe la ecuación de la línea.	$.$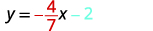
Identificar la pendiente.	$.$
Identificar la intercepción y.	$.$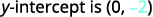

ⓑ Cuando una ecuación de una línea no se da en forma de pendiente-intercepción, nuestro primer paso será resolver la ecuación para y.

Resolver por y.	x+3y=9x+3y=9
Restar x de cada lado.	$.$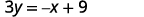
Divide ambos lados por 3.	$.$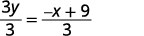
Simplificar.	$.$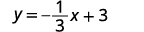
Escriba la forma pendiente-intercepción de la ecuación de la línea.	$.$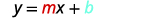
Escribe la ecuación de la línea.	$.$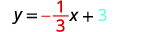
Identificar la pendiente.	$.$
Identificar la intercepción y.	$.$

Ejemplo$\PageIndex{14}$

Identificar la pendiente y -intercepción a partir de la ecuación de la línea.

ⓐ$y=\frac{2}{5}x−1$ ⓑ$x+4y=8$

Responder: ⓐ$m=\frac{2}{5}$;$(0,−1)$
ⓑ$m=−\frac{1}{4}$;$(0,2)$

Ejemplo$\PageIndex{15}$

Identificar la pendiente y -intercepción a partir de la ecuación de la línea.

ⓐ$y=−\frac{4}{3} x+1$ ⓑ$3x+2y=12$

Responder: ⓐ$m=−\frac{4}{3}$;$(0,1)$
ⓑ$m=−\frac{3}{2}$;$(0,6)$

Hemos graficado una línea usando la pendiente y un punto. Ahora que sabemos encontrar la pendiente y la intercepción y de una línea a partir de su ecuación, podemos usar la intercepción y como punto, y luego contar la pendiente a partir de ahí.

Ejemplo$\PageIndex{16}$

Grafica la línea de la ecuación$y=−x+4$ using its slope and y -interceptar.

Responder

	$y=mx+b$
La ecuación está en forma de pendiente-intercepción.	$y=−x+4$
Identificar la pendiente y -intercepción.	$m=−1$ y -intercepción es$(0,4)$
Trazar la intercepción y.	Ver la gráfica.
Identificar la subida sobre la carrera.	$m=−11$
Cuenta la subida y corre para marcar el segundo punto.	subir$-1$, correr$1$ $.$

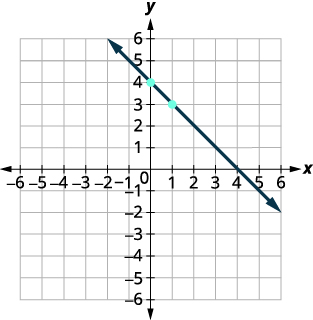
Dibuja la línea como se muestra en la gráfica.

Ejemplo$\PageIndex{17}$

Grafica la línea de la ecuación$y=−x−3$ usando su pendiente y -intercepción.

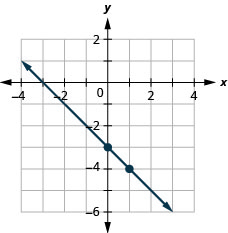
Responder: $Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 10 a 10. El eje y va de negativo 10 a 10. La línea pasa por los puntos (0, negativo 3) y (1, negativo 4).$

Ejemplo$\PageIndex{18}$

Grafica la línea de la ecuación$y=−x−1$ usando su pendiente y -intercepción.

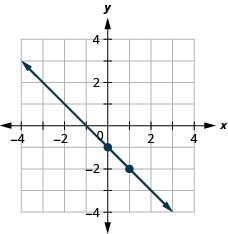
Responder: $Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 10 a 10. El eje y va de negativo 10 a 10. La línea pasa por los puntos (0, negativo 1) y (1, negativo 2).$

Ahora que hemos graficado líneas usando la pendiente y la intercepción y, vamos a resumir todos los métodos que hemos utilizado para graficar líneas.

$La tabla tiene una fila de título que dice “Métodos para graficar líneas”. Debajo de esto hay cuatro columnas. La primera columna contiene lo siguiente: Trazado de Puntos. Una mesa en blanco con dos columnas y cuatro filas. La primera fila es una fila de encabezado con los encabezados “x” e “y”. Encuentra tres puntos. Traza los puntos, asegúrate de que se alineen, ellos dibujan la línea. La segunda columna contiene: Inclinación-Intercepción. Y es igual a m x más b. Encuentra la pendiente y la intersección y, luego, cuenta la pendiente para obtener un segundo punto. La tercera columna: Intercepta. Una mesa con dos columnas y cuatro filas. La primera fila es una fila de encabezado con los encabezados “x” e “y”. En la primera fila hay un 0 en la columna x. En la segunda fila hay un 0 en la columna y. Los espacios restantes están en blanco. Cuarta columna. Reconocer líneas verticales y horizontales. La ecuación tiene sólo una variable. X equivale a una vertical. Y es igual a b horizontal.$

Elija el método más conveniente para graficar una línea

Ahora que hemos visto varios métodos que podemos usar para graficar líneas, ¿cómo sabemos qué método usar para una ecuación dada?

Si bien podríamos trazar puntos, usar la forma pendiente-interceptar o encontrar las intercepciones para cualquier ecuación, si reconocemos la forma más conveniente de graficar un cierto tipo de ecuación, nuestro trabajo será más fácil.

Generalmente, trazar puntos no es la forma más eficiente de graficar una línea. Busquemos algunos patrones para ayudar a determinar el método más conveniente para graficar una línea.

Aquí hay cinco ecuaciones que graficamos en este capítulo, y el método que usamos para graficar cada una de ellas.

\[ \begin{array} {lll} {} &{\textbf{Equation}} &{\textbf{Method}} \\ {\text{#1}} &{x=2} &{\text{Vertical line}} \\ {\text{#2}} &{y=−1} &{\text{Horizontal line}} \\ {\text{#3}} &{−x+2y=6} &{\text{Intercepts}} \\ {\text{#4}} &{4x−3y=12} &{\text{Intercepts}} \\ {\text{#5}} &{y=−x+4} &{\text{Slope–intercept}} \\ \end{array} \nonumber\]

Las ecuaciones #1 y #2 tienen cada una solo una variable. Recuerde, en ecuaciones de esta forma el valor de esa variable es constante; no depende del valor de la otra variable. Las ecuaciones de esta forma tienen gráficas que son líneas verticales u horizontales.

En las ecuaciones #3 y #4, tanto x como y están en el mismo lado de la ecuación. Estas dos ecuaciones son de la forma Ax+By=C.Ax+By=C. sustituimos y=0y=0 para encontrar el x - intercept y x=0x=0 para encontrar el y -intercept, y luego encontramos un tercer punto eligiendo otro valor para x o y.

La ecuación #5 está escrita en forma pendiente-intercepción. Después de identificar la pendiente y la intersección y a partir de la ecuación las usamos para graficar la línea.

Esto lleva a la siguiente estrategia.

Estrategia para elegir el método más conveniente para graficar una línea

Considera la forma de la ecuación.

Si sólo tiene una variable, es una línea vertical u horizontal.
- $x=a$es una línea vertical que pasa a través del eje x en a.
- $y=b$es una línea horizontal que pasa por el eje y en b.
Si y se aísla en un lado de la ecuación, en la forma$y=mx+b$, grafica usando la pendiente y -intercepción.
- Identificar la pendiente y -interceptar y luego graficar.
Si la ecuación es de la forma$Ax+By=C$, encuentra las intercepciones.
- Encuentra las intercepciones x e y, un tercer punto, y luego grafica.

Ejemplo$\PageIndex{19}$

Determine el método más conveniente para graficar cada línea:

ⓐ$y=5$ ⓑ$4x−5y=20$ ⓒ$x=−3$ ⓓ$y=−\frac{5}{9}x+8$

Responder: ⓐ$y=5$
Esta ecuación tiene sólo una variable, y. Su gráfica es una línea horizontal que cruza el eje y en$5$.
ⓑ$4x−5y=20$
Esta ecuación es de la forma$Ax+By=C$. La forma más fácil de graficarlo será encontrar las intercepciones y un punto más.
ⓒ Sólo$x=−3$
hay una variable, x. La gráfica es una línea vertical que cruza el eje x en$−3$.
ⓓ$y=−\frac{5}{9}x+8$
Dado que esta ecuación está en$y=mx+b$ forma, será más fácil graficar esta línea usando la pendiente y las intercepciones y.

Ejemplo$\PageIndex{20}$

Determine el método más conveniente para graficar cada línea:

ⓐ$3x+2y=12$ ⓑ$y=4$ ⓒ$y=\frac{1}{5}x−4$ ⓓ$x=−7$.

Responder: ⓐ intercepta ⓑ línea horizontal ⓒ pendiente-intersección ⓓ línea vertical

Ejemplo$\PageIndex{21}$

Determine el método más conveniente para graficar cada línea:

ⓐ$x=6$ ⓑ$y=−\frac{3}{4}x+1$ ⓒ$y=−8$ ⓓ$4x−3y=−1$.

Responder: ⓐ línea vertical ⓑ pendiente-intercepción ⓒ línea horizontal
ⓓ intercepciones

Gráfica e Interpreta Aplicaciones de Inclinación-Intercepción

Muchas aplicaciones del mundo real están modeladas por ecuaciones lineales. Echaremos un vistazo a algunas aplicaciones aquí para que pueda ver cómo las ecuaciones escritas en forma de pendiente-intercepción se relacionan con situaciones del mundo real.

Por lo general, cuando un modelo de ecuación lineal utiliza datos del mundo real, se utilizan letras diferentes para las variables, en lugar de usar solo x e y. Los nombres de las variables nos recuerdan qué cantidades se están midiendo.

Además, a menudo necesitaremos extender los ejes en nuestro sistema de coordenadas rectangulares a números positivos y negativos más grandes para acomodar los datos en la aplicación.

Ejemplo$\PageIndex{22}$

La ecuación$F=\frac{9}{5}C+32$ se utiliza para convertir temperaturas, C, en la escala Celsius a temperaturas, F, en la escala Fahrenheit.

ⓐ Encuentra la temperatura Fahrenheit para una temperatura Celsius de 0.

ⓑ Encuentra la temperatura Fahrenheit para una temperatura Celsius de 20.

ⓓ Grafica la ecuación.

Responder

ⓐ

$ \begin{array} {ll} {\text{Find the Fahrenheit temperature for a Celsius temperature of 0.}} &{F=\frac{9}{5}C+32} \\ {\text{Find F when C=0.}} &{F=\frac{9}{5}(0)+32} \\ {\text{Simplify.}} &{F=32} \\ \end{array} \nonumber$

ⓑ

$ \begin{array} {ll} {\text{Find the Fahrenheit temperature for a Celsius temperature of 20.}} &{F=\frac{9}{5}C+32} \\ {\text{Find F when C=20.}} &{F=\frac{9}{5}(20)+32} \\ {\text{Simplify.}} &{F=36+32} \\ {\text{Simplify.}} &{F=68} \\ \end{array} \nonumber$

ⓒ
Interpretar la pendiente y F -intercepción de la ecuación.
A pesar de que esta ecuación usa F y C, todavía está en forma de pendiente-intercepción.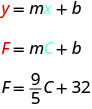

$y es igual a m x más b. F es igual a m C más b. Los y y F se enfatizan en rojo. La x y la C se enfatizan en azul. F equivale a 9 dividido por 5 C más 32.$

La pendiente,$\frac{9}{5}$, significa que la temperatura Fahrenheit (F) aumenta 9 grados cuando la temperatura Celsius (C) aumenta 5 grados.
La F -intercepción significa que cuando la temperatura está$0°$ en la escala Celsius, está$32°$ en la escala Fahrenheit.
ⓓ Grafica la ecuación.
Tendremos que usar una escala mayor que la habitual. Comienza en la intercepción F$(0,32)$, y luego cuenta la subida de 9 y la racha de 5 para obtener un segundo punto como se muestra en la gráfica.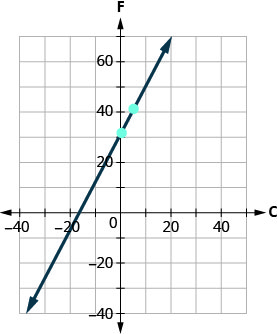

$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 40 a 80. El eje y va de negativo 40 a 80. La línea pasa por los puntos (0, 32) y (5, 41).$

Ejemplo$\PageIndex{23}$

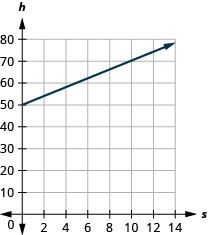
La ecuación$h=2s+50$ is used to estimate a woman’s height in inches, h, basada en su talla de zapato, s.

ⓐ Estimar la altura de un niño que usa zapatos de mujer talla 0.

ⓑ Estimar la altura de una mujer con talla de zapato 8.

ⓓ Grafica la ecuación.

Responder

ⓐ 50 pulgadas
ⓑ 66 pulgadas
ⓒ La pendiente, 2, significa que la altura, h, aumenta en 2 pulgadas cuando la talla del zapato, s, aumenta en 1. La intercepción h significa que cuando la talla de zapato es 0, la altura es de 50 pulgadas.
ⓓ

$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 1 a 14. El eje y va de 1 negativo a 80. La línea pasa por los puntos (0, 50) y (10, 70).$

Ejemplo$\PageIndex{24}$

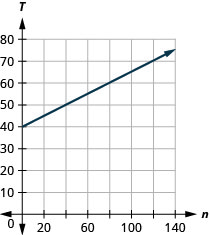
La ecuación$T=\frac{1}{4}n+40$ is used to estimate the temperature in degrees Fahrenheit, T, basada en el número de chirps de cricket, n, en un minuto.

ⓐ Estime la temperatura cuando no haya chirps.

ⓑ Estimar la temperatura cuando el número de chirps en un minuto es de 100.

ⓓ Grafica la ecuación.

Responder

ⓐ 40 grados
ⓑ 65 grados
ⓒ La pendiente,$\frac{1}{4}$, significa que la temperatura Fahrenheit (F) aumenta 1 grado cuando el número de chirps, n, aumenta en 4. La intersección en T significa que cuando el número de chirps es 0, la temperatura es de 40°.
ⓓ

$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de 1 negativo a 140. El eje y va de 1 negativo a 80. La línea pasa por los puntos (0, 40) y (40, 50).$

El costo de ejecutar algunos tipos de negocios tiene dos componentes: un costo fijo y un costo variable. El costo fijo es siempre el mismo independientemente de cuántas unidades se produzcan. Este es el costo de renta, seguro, equipo, publicidad y otros artículos que deben pagarse regularmente. El costo variable depende del número de unidades producidas. Es para el material y mano de obra necesarios para producir cada artículo.

Ejemplo$\PageIndex{25}$

Sam conduce una camioneta de reparto. La ecuación$C=0.5m+60$ modela la relación entre su costo semanal, C, en dólares y el número de millas, m, que conduce.

ⓐ Encuentra el costo de Sam por una semana cuando conduce 0 millas.

ⓑ Encuentra el costo por una semana cuando conduce 250 millas.

ⓓ Grafica la ecuación.

Responder

ⓐ
$ \begin{array} {ll} {\text{Find Sam’s cost for a week when he drives 0 miles.}} &{C=0.5m+60} \\ {\text{Find C when m=0.}} &{C=0.5(0)+60} \\ {\text{Simplify.}} &{C=60} \\ {} &{\text{Sam’s costs are }$\text{60 when he drives 0 miles.}} \\ \end{array} \nonumber $
ⓑ
$ \begin{array} {ll} {\text{Find Sam’s cost for a week when he drives 250 miles.}} &{C=0.5m+60} \\ {\text{Find C when m=250.}} &{C=0.5(250)+60} \\ {\text{Simplify.}} &{C=185} \\ {} &{\text{Sam’s costs are }$\text{185 when he drives 250 miles.}} \\ \end{array} \nonumber $
ⓒ Interpreta la pendiente y C -intercepción de la ecuación.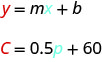

$y es igual a m x más b. C es igual a 0.5 p más 60. La y y la C se enfatizan en rojo. La x y la p se enfatizan en azul.$

La pendiente, 0.5, significa que el costo semanal, C, aumenta en $0.50 cuando el número de millas recorridas, n, aumenta en 1.
El C-intercepto significa que cuando el número de millas recorridas es 0, el costo semanal es de $60.
ⓓ Grafica la ecuación.
Tendremos que usar una escala mayor que la habitual. Comienza en la intercepción $(0,60)$C.

Para contar la pendiente$m= 0.5$, la reescribimos como una fracción equivalente que facilitará nuestra gráfica.

$ \begin{array} {ll} {} &{m=0.5} \\ {\text{Rewrite as a fraction.}} &{m=\frac{0.5}{1}} \\ {\text{Multiply numerator and}} &{} \\ {\text{denominator by 100}} &{m=\frac{0.5(100)}{1(100)}} \\ {\text{Simplify.}} &{m=\frac{50}{100}} \\ \end{array} \nonumber $

Entonces para graficar el siguiente punto subir 50 desde la intercepción de 60 y luego a la derecha 100. El segundo punto será$(100, 110)$.

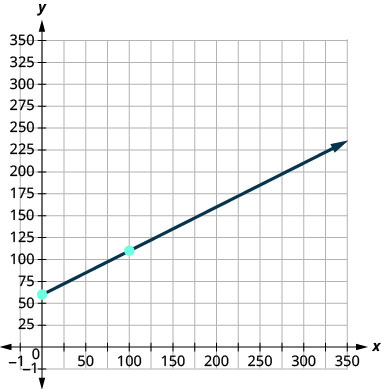
$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de 1 negativo a 350. El eje y va de 1 negativo a 350. La línea pasa por los puntos (0, 60) y (200, 160).$

Ejemplo$\PageIndex{26}$

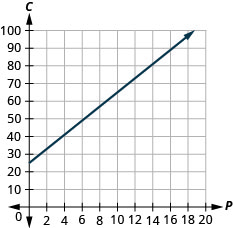
Stella tiene un negocio casero que vende pizzas gourmet. La ecuación$C=4p+25$ modela la relación entre su costo semanal, C, en dólares y el número de pizzas, p, que vende.

ⓐ Encuentra el costo de Stella por una semana cuando no vende pizzas.

ⓑ Encuentra el costo por una semana cuando vende 15 pizzas.

ⓓ Grafica la ecuación.

Responder

ⓐ $25
ⓑ $85
ⓒ La pendiente, 4, significa que el costo semanal, C, aumenta en $4 cuando el número de pizzas vendidas, p, aumenta en 1. El C-intercepto significa que cuando el número de pizzas vendidas es 0, el costo semanal es de $25.
ⓓ

$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de negativo 2 a 20. El eje y va de negativo 10 a `00. La línea pasa por los puntos (0, 25) y (1, 29).$

Ejemplo$\PageIndex{27}$

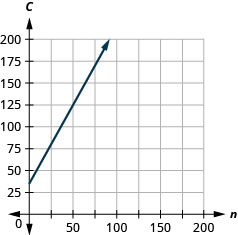
Loreen tiene un negocio de caligrafía. La ecuación$C=1.8n+35$ modela la relación entre su costo semanal, C, en dólares y el número de invitaciones de boda, n, que escribe.

ⓐ Encuentra el costo de Loreen para una semana cuando no escribe invitaciones.

ⓑ Encuentra el costo por una semana cuando escribe 75 invitaciones.

ⓓ Grafica la ecuación.

Responder

ⓐ $35
ⓑ $170
ⓒ La pendiente,$1.8$, significa que el costo semanal, C, aumenta$$1.80$ cuando el número de invitaciones, n, aumenta en 1.
El C-intercepto significa que cuando el número de invitaciones es 0, el costo semanal es de 35 dólares.
ⓓ

$Esta figura muestra la gráfica de una línea recta en el plano de la coordenada x y. El eje x va de 1 negativo a 350. El eje y va de 1 negativo a 350. La línea pasa por los puntos (0, 35) y (75, 170).$

Utilizar pendientes para identificar líneas paralelas y perpendiculares

Dos líneas que tienen la misma pendiente se denominan líneas paralelas. Las líneas paralelas tienen la misma pendiente y nunca se cruzan.

Esto lo decimos de manera más formal en términos del sistema de coordenadas rectangulares. Dos líneas que tienen la misma pendiente y diferentes intersecciones y se denominan líneas paralelas. Ver Figura.

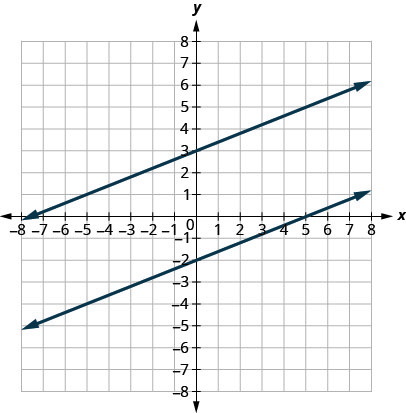
Esta figura muestra la gráfica de dos líneas rectas en el plano de la coordenada x y. El eje x va de negativo 8 a 8. El eje y va de negativo 8 a 8. La primera línea pasa por los puntos (0, 3) y (5, 5). La segunda línea pasa por los puntos (0, negativo 2) y (5, 0). Las líneas son paralelas, lo que significa que siempre estarán a la misma distancia y nunca se cruzarán. Están inclinadas por el mismo ángulo. — Figura$\PageIndex{3}$

Verifique que ambas líneas tengan la misma pendiente$m=\frac{2}{5}$,, y diferentes intercepciones y.

¿Qué pasa con las líneas verticales? La pendiente de una línea vertical es indefinida, por lo que las líneas verticales no encajan en la definición anterior. Decimos que las líneas verticales que tienen diferentes intercepciones x son paralelas, como las líneas que se muestran en esta gráfica.

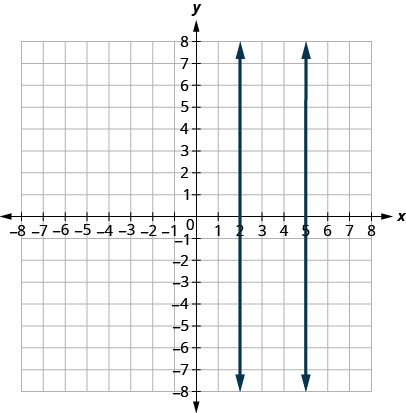
Esta figura muestra la gráfica de una línea vertical de dos rectas en el plano de la coordenada x y. El eje x va de negativo 8 a 8. El eje y va de negativo 8 a 8. La primera línea pasa por los puntos (2, 0) y (2, 1). La segunda línea pasa por los puntos (5, 0) y (5, 1). Las líneas son paralelas, lo que significa que siempre estarán a la misma distancia y nunca se cruzarán. — Figura$\PageIndex{4}$

LINEAS PARELAS

Las líneas paralelas son líneas en el mismo plano que no se cruzan.

Las líneas paralelas tienen la misma pendiente y diferentes intersecciones y.
Si m1m1 y m2m2 son las pendientes de dos líneas paralelas entonces m1=m2.m1=m2.
Las líneas verticales paralelas tienen diferentes intercepciones x

Dado que las líneas paralelas tienen la misma pendiente y diferentes intercepciones y, ahora solo podemos mirar la forma pendiente-interceptar de las ecuaciones de líneas y decidir si las líneas son paralelas.

Ejemplo$\PageIndex{28}$

Utilice pendientes e intercepciones y para determinar si las líneas son paralelas:

ⓐ$3x−2y=6$ y$y=\frac{3}{2}x+1$ ⓑ$y=2x−3$ y$−6x+3y=−9$.

Responder: ⓐ
$ \begin{array} {llll} {} &{3x−2y=6} &{\text{and}} &{y=\frac{3}{2}x+1} \\ {} &{−2y=−3x+6} &{} &{} \\ {\text{Solve the first equation for y.}} &{\frac{-2y}{-2}=\frac{-3x+6}{-2}} &{} &{} \\ {\text{The equation is now in slope–intercept form.}} &{y=\frac{3}{2}x−3} &{} &{} \\ {\text{The equation of the second line is already}} &{} &{} &{} \\ {\text{in slope–intercept form.}} &{} &{} &{y=\frac{3}{2}x+1} \\ {} &{} &{} &{} \\ {} &{y=\frac{3}{2}x−3} &{} &{y=\frac{3}{2}x+1} \\ {Identify the slope andy-intercept of both lines.} &{y=mx+b} &{} &{y=mx+b} \\ {} &{m=\frac{3}{2}} &{} &{y=\frac{3}{2}} \\ {} &{\text{y-intercept is }(0,−3)} &{} &{\text{y-intercept is }(0,1)} \\ \end{array} \nonumber$
Las líneas tienen la misma pendiente y diferentes intersecciones y por lo tanto son paralelas.
Es posible que desee graficar las líneas para confirmar si son paralelas.

ⓑ
$ \begin{array} {llll} {} &{y=2x−3} &{\text{and}} &{−6x+3y=−9} \\ {\text{The first equation is already in slope–intercept form.}} &{y=2x−3} &{} &{} \\ {} &{} &{} &{−6x+3y=−9} \\ {} &{} &{} &{3y=6x−9} \\ {\text{Solve the second equation for y.}} &{} &{} &{\frac{3y}{3}=\frac{6x−9}{3}} \\ {} &{} &{} &{y=2x−3} \\ {\text{The second equation is now in slope–intercept form.}} &{} &{} &{y=2x−3} \\ {} &{} &{} &{} \\ {} &{y=2x−3} &{} &{y=2x−3} \\ {\text{Identify the slope andy-intercept of both lines.}} &{y=mx+b} &{} &{y=mx+b} \\ {} &{m=2} &{} &{m=2} \\ {} &{\text{y-intercept is }(0,−3)} &{} &{\text{y-intercept is }(0,-3)} \\ \end{array} \nonumber$
Las líneas tienen la misma pendiente, pero también tienen las mismas intersecciones y. Sus ecuaciones representan la misma línea y decimos que las líneas son coincidentes. No son paralelos; son la misma línea.

Ejemplo$\PageIndex{29}$

Utilice pendientes e intercepciones y para determinar si las líneas son paralelas:

ⓐ$2x+5y=5$ y$y=−\frac{2}{5}x−4$ ⓑ$y=−\frac{1}{2}x−1$ y$x+2y=−2$.

Responder: ⓐ paralelo ⓑ no paralelo; misma línea

Ejemplo$\PageIndex{30}$

Utilice pendientes e intercepciones y para determinar si las líneas son paralelas:

ⓐ$4x−3y=6$ y$y=\frac{4}{3}x−1$ ⓑ$y=\frac{3}{4}x−3$ y$3x−4y=12$.

Responder: ⓐ paralelo ⓑ no paralelo; misma línea

Ejemplo$\PageIndex{31}$

Utilice pendientes e intercepciones y para determinar si las líneas son paralelas:

ⓐ$y=−4$ y$y=3$ ⓑ$x=−2$ y$x=−5$.

Responder

ⓐ$y=−4$ y$y=3$

Reconocemos de inmediato de las ecuaciones que estas son líneas horizontales, y así sabemos que sus pendientes son ambas 0.
Dado que las líneas horizontales cruzan el eje y en y=−4y=−4 y en y=3, y=3, sabemos que las intercepciones y son (0, −4) (0, −4) y (0,3). (0,3).
Las líneas tienen la misma pendiente y diferentes intersecciones y por lo tanto son paralelas.

ⓑ$x=−2$ y$x=−5$

Reconocemos enseguida de las ecuaciones que se trata de líneas verticales, y así sabemos que sus pendientes son indefinidas.
Dado que las líneas verticales cruzan el eje x en$x=−2$ y$x=−5$, sabemos que las intercepciones$(−2,0)$ y son y$(−5,0)$.
Las líneas son verticales y tienen diferentes intercepciones x y por lo tanto son paralelas.

Ejemplo$\PageIndex{32}$

Utilice pendientes e intercepciones y para determinar si las líneas son paralelas:

ⓐ$y=8$ y$y=−6$ ⓑ$x=1$ y$x=−5$.

Responder: ⓐ paralelo ⓑ paralelo

Ejemplo$\PageIndex{33}$

Utilice pendientes e intercepciones y para determinar si las líneas son paralelas:

ⓐ$y=1$ y$y=−5$ ⓑ$x=8$ y$x=−6$.

Responder: ⓐ paralelo ⓑ paralelo

Veamos las líneas cuyas ecuaciones son$y=\frac{1}{4}x−1$ y$y=−4x+2$, mostradas en la Figura.

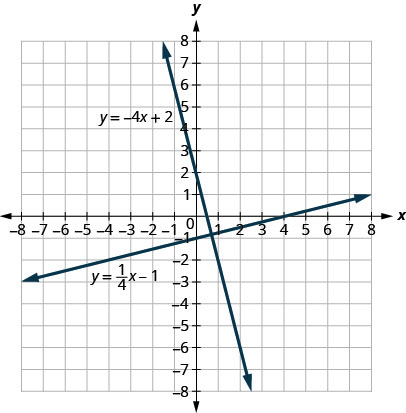
Esta figura muestra la gráfica de dos líneas rectas perpendiculares en el plano de la coordenada x y. El eje x va de negativo 8 a 8. El eje y va de negativo 8 a 8. La primera línea pasa por los puntos (0, negativo 1) y (4, 0). La primera línea está etiquetada y es igual a 1 dividido por 4 x menos 1. La segunda línea pasa por los puntos (0, 2) y (1, negativo 2). La segunda línea está etiquetada y es igual a negativo 4 x más 2. Las líneas son perpendiculares, lo que significa que forman un ángulo recto donde se cruzan. — Figura$\PageIndex{5}$

Estas líneas se encuentran en el mismo plano y se cruzan en ángulos rectos. A estas líneas las llamamos perpendiculares.

Si miramos la pendiente de la primera línea,$m_1=\frac{1}{4}$, y la pendiente de la segunda línea$m_2=−4$,, podemos ver que son recíprocos negativos entre sí. Si los multiplicamos, su producto lo es$−1$.

\[\begin{array} {l} {m_1·m_2} \\ {14(−4)} \\ {−1} \\ \end{array} \nonumber\]

Esto siempre es cierto para las líneas perpendiculares y nos lleva a esta definición.

LÍNEAS PERP

Las líneas perpendiculares son líneas en el mismo plano que forman un ángulo recto.

Si$m_1$ y$m_2$ son las pendientes de dos líneas perpendiculares, entonces:
- sus pendientes son recíprocos negativos entre sí,$m_1=−\frac{1}{m_2}$.
- el producto de sus pendientes es$−1$,$m_1·m_2=−1$.
Una línea vertical y una línea horizontal son siempre perpendiculares entre sí

Pudimos observar la forma pendiente-intercepción de las ecuaciones lineales y determinar si las líneas eran paralelas o no. Podemos hacer lo mismo para las líneas perpendiculares.

Encontramos la forma pendiente-intercepción de la ecuación, y luego vemos si las pendientes son recíprocas opuestas. Si el producto de las pendientes es$−1$, las líneas son perpendiculares.

Ejemplo$\PageIndex{34}$

Utilice pendientes para determinar si las líneas son perpendiculares:

ⓐ$y=−5x−4$ y$x−5y=5$ ⓑ$7x+2y=3$ y$2x+7y=5$

Responder: ⓐ
La primera ecuación está en forma pendiente-intercepto.Resuelve la segunda ecuación.Identifica la pendiente de cada línea.Y=−5x−4YYm1=−5x−4=mx+b=−5x−5y−5y−5y−5y=5=−x+5=−x+5 = 15x−1Yym2=15x−1=mx+b=15x−1=mx+b=15x−1=mx+b=15x−1=mx+b=15x−1=mx+b=15está en forma pendiente-intercepto.Y=−5x−4Resuelve la segunda ecuación pory.x−5y=5−5y=−x+5−5y−5=−x+5 −5y=15x−1Identificar la pendiente de cada línea.y=−5x−4y=mx+bm1=−5y=15x−1y=mx+bm2=15
Las pendientes son recíprocas negativas entre sí, por lo que las líneas son perpendiculares. Comprobamos multiplicando las pendientes, Desde −5 (15) =−1, −5 (15) =−1, comprueba.

ⓑ
Resuelve las ecuaciones fory.Identifica la pendiente de cada línea.7x+2y2y2y=3=−7x+3=−7x+32=−72x+32yM1=mx+b=−722x+7y7y7y=5=−2x+5=−2x+57=−27x+57=−27x+57ym1=mx+b=−27Resuelve las ecuaciones para Y.7x+2y=32y=−7x+32y2=−7x+32y=−72x+322x+7y=57y=−2x+57y7=−2x+57y=−27x+57Identificar la pendiente de cada línea.y=mx+bm1=−72y=mx+bm1=−27
Las pendientes son recíprocas entre sí, pero tienen el mismo signo. Al no ser recíprocos negativos, las líneas no son perpendiculares.

Ejemplo$\PageIndex{3}$

Utilice pendientes para determinar si las líneas son perpendiculares:

ⓐ$y=−3x+2$ y$x−3y=4$ ⓑ$5x+4y=1$ y$4x+5y=3$.

Responder: ⓐ perpendicular ⓑ no perpendicular

Ejemplo$\PageIndex{3}$

Utilice pendientes para determinar si las líneas son perpendiculares:

ⓐ$y=2x−5$ y$x+2y=−6$ ⓑ$2x−9y=3$ y$9x−2y=1$.

Responder: ⓐ perpendicular ⓑ no perpendicular

Conceptos clave

Pendiente de una Línea
- La pendiente de una línea es$m=\frac{\text{rise}}{\text{run}}$.
- La subida mide el cambio vertical y la corrida mide el cambio horizontal.
Cómo encontrar la pendiente de una línea a partir de su gráfica utilizando$m=\frac{\text{rise}}{\text{run}}$.
1. Localice dos puntos en la línea cuyas coordenadas sean números enteros.
2. Comenzando con un punto, esboza un triángulo rectángulo, yendo del primer punto al segundo punto.
3. Cuenta la subida y la carrera en las piernas del triángulo.
4. Toma la relación de subida para correr para encontrar la pendiente:$m=\frac{\text{rise}}{\text{run}}$.

Pendiente de una línea entre dos puntos.
- La pendiente de la línea entre dos puntos$(x_1,y_1)$ y$(x_2,y_2)$ es:
  \[m=\frac{y_2−y_1}{x_2−x_1} \nonumber\].
Cómo graficar una línea dada un punto y la pendiente.
1. Trazar el punto dado.
2. Utilice la fórmula de pendiente$m=\frac{\text{rise}}{\text{run}}$ para identificar la subida y la carrera.
3. Comenzando en el punto dado, cuente la subida y corra para marcar el segundo punto.
4. Conecta los puntos con una línea.
Forma de intersección de pendiente de una ecuación de una línea
- La forma pendiente-intercepción de una ecuación de una línea con pendiente m e intercepción y,$(0,b)$ es$y=mx+b$
- $La tabla tiene una fila de título que dice “Métodos para graficar líneas”. Debajo de esto hay cuatro columnas. La primera columna contiene lo siguiente: Trazado de Puntos. Una mesa en blanco con dos columnas y cuatro filas. La primera fila es una fila de encabezado con los encabezados “x” e “y”. Encuentra tres puntos. Traza los puntos, asegúrate de que se alineen, ellos dibujan la línea. La segunda columna contiene: Inclinación-Intercepción. Y es igual a m x más b. Encuentra la pendiente y la intersección y, luego, cuenta la pendiente para obtener un segundo punto. La tercera columna: Intercepta. Una mesa con dos columnas y cuatro filas. La primera fila es una fila de encabezado con los encabezados “x” e “y”. En la primera fila hay un 0 en la columna x. En la segunda fila hay un 0 en la columna y. Los espacios restantes están en blanco. Cuarta columna. Reconocer líneas verticales y horizontales. La ecuación tiene sólo una variable. X equivale a una vertical. Y es igual a b horizontal.$
Líneas Paralelas
- Las líneas paralelas son líneas en el mismo plano que no se cruzan.
  Las líneas paralelas tienen la misma pendiente y diferentes intersecciones y.
  Si$m_1$ y$m_2$ son las pendientes de dos líneas paralelas entonces$m_1=m_2$.
  Las líneas verticales paralelas tienen diferentes intercepciones x.
Líneas perpendiculares
- Las líneas perpendiculares son líneas en el mismo plano que forman un ángulo recto.
- Si$m_1$ y$m_2$ son las pendientes de dos líneas perpendiculares, entonces:
  sus pendientes son recíprocos negativos entre sí,$m_1=−\frac{1}{m_2}$.
  el producto de sus pendientes es$−1$,$m_1·m_2=−1$.
- Una línea vertical y una línea horizontal son siempre perpendiculares entre sí.

Glosario

líneas paralelas: Las líneas paralelas son líneas en el mismo plano que no se cruzan.

líneas perpendiculares: Las líneas perpendiculares son líneas en el mismo plano que forman un ángulo recto.

Localice dos puntos en la gráfica cuyas coordenadas sean números enteros.	\((0,5)\)y\((3,3)\)
A partir de\((0,5)\), esboce un triángulo rectángulo \((3,3)\) como se muestra en esta gráfica.	$.$
Cuenta la subida— ya que baja, es negativo.	El ascenso es\(−2\).
Cuenta la carrera.	La carrera es 3.
Utilice la fórmula de pendiente.	\(m=\frac{\text{rise}}{\text{run}}\)
Sustituir los valores de la subida y corrida.	\(m=−23\)
Simplificar.	\(m=−23\)
	La pendiente de la línea es\(−23\).
	Entonces y disminuye en 2 unidades a medida que x aumenta en 3 unidades.

	\(y=mx+b\)
La ecuación está en forma de pendiente-intercepción.	\(y=−x+4\)
Identificar la pendiente y -intercepción.	\(m=−1\) y -intercepción es\((0,4)\)
Trazar la intercepción y.	Ver la gráfica.
Identificar la subida sobre la carrera.	\(m=−11\)
Cuenta la subida y corre para marcar el segundo punto.	subir\(-1\), correr\(1\) $.$

Objetivos de aprendizaje

Encuentra la Talud de una Línea

PENDIENTE DE UNA LÍNEA

ENCUENTRA LA PENDIENTE DE UNA LÍNEA A PARTIR\(m=\frac{\text{rise}}{\text{run}}\)

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\)

Talud de una línea horizontal y vertical

Ejemplo\(\PageIndex{4}\)

Ejemplo\(\PageIndex{5}\)

Ejemplo\(\PageIndex{6}\)

GUÍA RÁPIDA DE LAS PISTAS DE

Talud de una línea entre dos puntos

Ejemplo\(\PageIndex{7}\)

Ejemplo\(\PageIndex{9}\)

Graficar una línea dado un punto y el talud

Ejemplo\(\PageIndex{10}\): How to graph a Line Given a Point and the Slope

Ejemplo\(\PageIndex{11}\)

Ejemplo\(\PageIndex{12}\)

GRÁFICA UNA LÍNEA DADA UN PUNTO Y LA T

Graficar una línea usando su pendiente e intercepción

FORMA DE INTERCEPCIÓN DE PENDIENTE DE UNA ECUACIÓN DE

Ejemplo\(\PageIndex{13}\)

Ejemplo\(\PageIndex{14}\)

Ejemplo\(\PageIndex{15}\)

Ejemplo\(\PageIndex{16}\)

Ejemplo\(\PageIndex{17}\)

Ejemplo\(\PageIndex{18}\)

Elija el método más conveniente para graficar una línea

Estrategia para elegir el método más conveniente para graficar una línea

Ejemplo\(\PageIndex{19}\)

Ejemplo\(\PageIndex{20}\)

Ejemplo\(\PageIndex{21}\)

Gráfica e Interpreta Aplicaciones de Inclinación-Intercepción

Ejemplo\(\PageIndex{22}\)

Ejemplo\(\PageIndex{23}\)

Ejemplo\(\PageIndex{24}\)

Ejemplo\(\PageIndex{25}\)

Ejemplo\(\PageIndex{26}\)

Ejemplo\(\PageIndex{27}\)

Utilizar pendientes para identificar líneas paralelas y perpendiculares

LINEAS PARELAS

Ejemplo\(\PageIndex{28}\)

Ejemplo\(\PageIndex{29}\)

Ejemplo\(\PageIndex{30}\)

Ejemplo\(\PageIndex{31}\)

Ejemplo\(\PageIndex{32}\)

Ejemplo\(\PageIndex{33}\)

LÍNEAS PERP

Ejemplo\(\PageIndex{34}\)

Ejemplo\(\PageIndex{3}\)

Ejemplo\(\PageIndex{3}\)

Conceptos clave

Glosario