3.4E: Ejercicios

Última actualización
Guardar como PDF

Page ID: 112278

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

La práctica hace la perfección

Encontrar una ecuación de la línea dada la pendiente y -Intercepción

En los siguientes ejercicios, encuentra la ecuación de una línea con pendiente dada e intercepción y. Escribe la ecuación en forma de pendiente-intercepción.

1. pendiente$3$ e$y$ -intercepción$(0,5)$

Contestar: $y=3x+5$

2. pendiente$8$ e$y$ -intercepción$(0,−6)$

3. pendiente$−3$ e$y$ -intercepción$(0,−1)$

Contestar: $y=−3x−1$

4. pendiente$−1$ e$y$ -intercepción$(0,3)$

5. pendiente$\frac{1}{5}$ e$y$ -intercepción$(0,−5)$

Contestar: $y=\frac{1}{5}x−5$

6. pendiente$−\frac{3}{4}$ e$y$ -intercepción$(0,−2)$

7. pendiente$0$ e$y$ -intercepción$(0,−1)$

Contestar: $y=−1$

8. pendiente$−4$ e$y$ intercepción$(0,0)$

En los siguientes ejercicios, encuentra la ecuación de la línea que se muestra en cada gráfica. Escribe la ecuación en forma de pendiente-intercepción.

9.
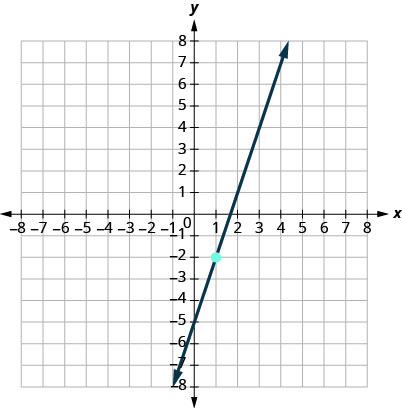
$Esta figura tiene una gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. La línea pasa por los puntos (0, negativo 5), (1, negativo 2) y (2, 1).$

Contestar: $y=3x−5$

10.
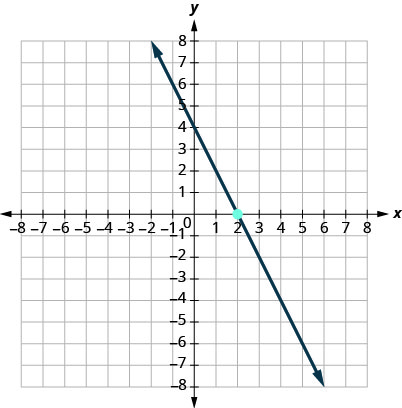
$Esta figura tiene una gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. La línea pasa por los puntos (0, 4), (1, 2) y (2, 0).$

11.
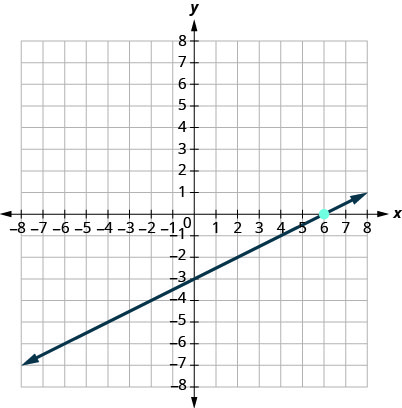
$Esta figura tiene una gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. La línea pasa por los puntos (0, negativo 3), (2, negativo 2) y (6, 0).$

Contestar: $y=\frac{1}{2}x−3$

12.
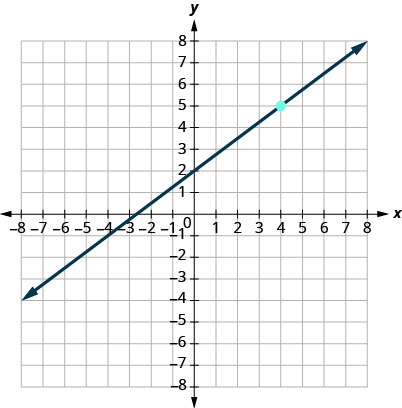
$Esta figura tiene una gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. La línea pasa por los puntos (0, 2), (4, 5) y (8, 8).$

13.
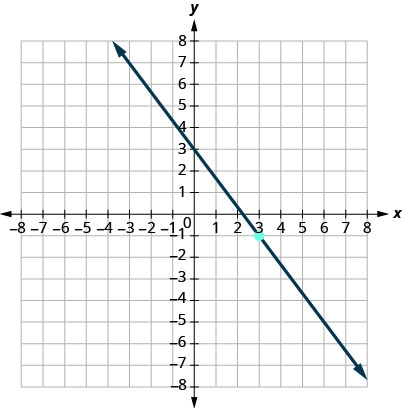
$Esta figura tiene una gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. La línea pasa por los puntos (0, 3), (3, negativo 1) y (6, negativo 5).$

Contestar: $y=−\frac{4}{3}x+3$

14.
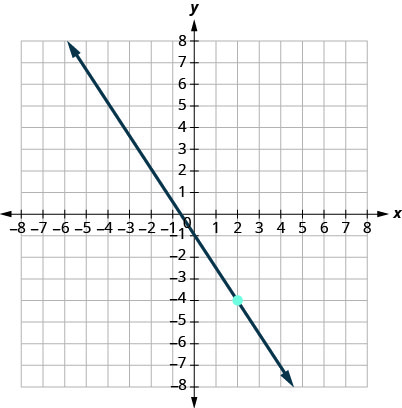
$Esta figura tiene una gráfica de una línea recta en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. La línea pasa por los puntos (0, negativo 1), (2, negativo 4) y (4, negativo 7).$

15.
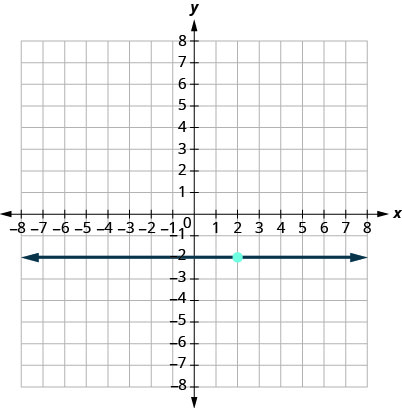
$Esta figura tiene una gráfica de una línea recta horizontal en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. La línea pasa por los puntos (0, negativo 2), (1, negativo 2) y (2, negativo 2).$

Contestar: $y=−2$

16.
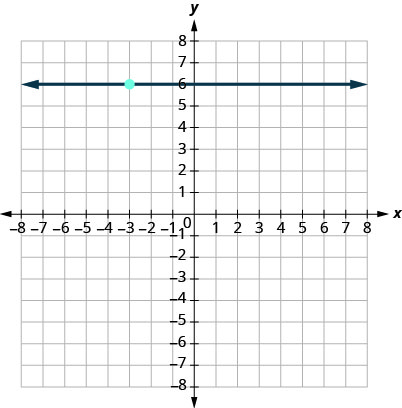
$Esta figura tiene una gráfica de una línea recta horizontal en el plano de la coordenada x y. Los ejes x e y van de negativo 10 a 10. La línea pasa por los puntos (0, 6), (1, 6) y (2, 6).$

Encontrar una ecuación de la línea dada la pendiente y un punto

En los siguientes ejercicios, encuentra la ecuación de una línea con pendiente dada y que contiene el punto dado. Escribe la ecuación en forma de pendiente-intercepción.

17. $m=\frac{5}{8}$, punto$(8,3)$

Contestar: $y=\frac{5}{8}x−2$

18. $m=\frac{5}{6}$, punto$(6,7)$

19. $m=−\frac{3}{5}$, punto$(10,−5)$

Contestar: $y=−\frac{3}{5}x+1$

20. $m=−\frac{3}{4}$, punto$(8,−5)$

21. $m=−\frac{3}{2}$, punto$(−4,−3)$

Contestar: $y=−\frac{3}{2}x+9$

22. $m=−\frac{5}{2}$, punto$(−8,−2)$

23. $m=−7$, punto$(−1,−3)$

Contestar: $y=−7x−10$

24. $m=−4$, punto$(−2,−3)$

25. Línea horizontal que contiene$(−2,5)$

Contestar: $y=5$

26. Línea horizontal que contiene$(−2,−3)$

27. Línea horizontal que contiene$(−1,−7)$

Contestar: $y=−7$

28. Línea horizontal que contiene$(4,−8)$

Encontrar una ecuación de la línea dada dos puntos

En los siguientes ejercicios, encuentra la ecuación de una línea que contiene los puntos dados. Escribe la ecuación en forma de pendiente-intercepción.

29. $(2,6)$y$(5,3)$

Contestar: $y=−x+8$

30. $(4,3)$y$(8,1)$

31. $(−3,−4)$y$(5−2)$.

Contestar: $y=\frac{1}{4}x−\frac{13}{4}$

32. $(−5,−3)$y$(4,−6)$.

33. $(−1,3)$y$(−6,−7)$.

Contestar: $y=2x+5$

34. $(−2,8)$y$(−4,−6)$.

35. $(0,4)$y$(2,−3)$.

Contestar: $y=−\frac{7}{2}x+4$

36. $(0,−2)$y$(−5,−3)$.

37. $(7,2)$y$(7,−2)$.

Contestar: $x=7$

38. $(−2,1)$y$(−2,−4)$.

39. $(3,−4)$y$(5,−4)$.

Contestar: $y=−4$

40. $(−6,−3)$y$(−1,−3)$

Encontrar una ecuación de una línea paralela a una línea dada

En los siguientes ejercicios, encuentra una ecuación de una línea paralela a la línea dada y contiene el punto dado. Escribe la ecuación en forma de pendiente-intercepción.

41. línea$y=4x+2$, punto$(1,2)$

Contestar: $y=4x−2$

42. línea$y=−3x−1$, punto$2,−3)$.

43. línea$2x−y=6$, punto$(3,0)$.

Contestar: $y=2x−6$

44. línea$2x+3y=6$, punto$(0,5)$.

45. línea$x=−4$, punto$(−3,−5)$.

Contestar: $x=−3$

46. línea$x−2=0$, punto$(1,−2)$

47. línea$y=5$, punto$(2,−2)$

Contestar: $y=−2$

48. línea$y+2=0$, punto$(3,−3)$

Encontrar una ecuación de una línea perpendicular a una línea dada

En los siguientes ejercicios, encuentra una ecuación de una línea perpendicular a la línea dada y contiene el punto dado. Escribe la ecuación en forma de pendiente-intercepción.

49. línea$y=−2x+3$, punto$(2,2)$

Contestar: $y=\frac{1}{2}x+1$

50. línea$y=−x+5$, punto$(3,3)$

51. Línea$y=\frac{3}{4}x−2$, punto$(−3,4)$

Contestar: $y=−\frac{4}{3}x$

52. línea$y=\frac{2}{3}x−4$, punto$(2,−4)$

53. línea$2x−3y=8$, punto$(4,−1)$

Contestar: $y=−\frac{3}{2}x+5$

54. línea$4x−3y=5$, punto$(−3,2)$

55. línea$2x+5y=6$, punto$(0,0)$

Contestar: $y=\frac{5}{2}x$

56. línea$4x+5y=−3$, punto$(0,0)$

57. línea$x=3$, punto$(3,4)$

Contestar: $y=4$

58. línea$x=−5$, punto$(1,−2)$

59. línea$x=7$, punto$(−3,−4)$

Contestar: $y=−4$

60. línea$x=−1$, punto$(−4,0)$

61. línea$y−3=0$, punto$(−2,−4)$

Contestar: $x=−2$

62. línea$y−6=0$, punto$(−5,−3)$

63. línea$y$ -eje, punto$(3,4)$

Contestar: $y=4$

64. línea$y$ -eje, punto$(2,1)$

Práctica Mixta

En los siguientes ejercicios, encuentra la ecuación de cada línea. Escribe la ecuación en forma de pendiente-intercepción.

65. Conteniendo los puntos$(4,3)$ y$(8,1)$

Contestar: $y=−\frac{1}{2}x+5$

66. Conteniendo los puntos$(−2,0)$ y$(−3,−2)$

67. $m=\frac{1}{6}$, que contiene punto$(6,1)$

Contestar: $y=\frac{1}{6}x$

68. $m=\frac{5}{6}$, que contiene punto$(6,7)$

69. Paralelo a la línea$4x+3y=6$, que contiene punto$(0,−3)$

Responder: $y=−\frac{4}{3}x−3$

70. Paralelo a la línea$2x+3y=6$, que contiene punto$(0,5)$

71. $m=−\frac{3}{4}$, que contiene punto$(8,−5)$

Responder: $y=−\frac{3}{4}x+1$

72. $m=−\frac{3}{5}$, que contiene punto$(10,−5)$

73. perpendicular a la línea$y−1=0$, punto$(−2,6)$

Responder: $x=−2$

74. perpendicular a la línea eje y, punto$(−6,2)$

75. Paralelo a la línea$x=−3$, que contiene punto$(−2,−1)$

Responder: $x=−2$

76. Paralelo a la línea$x=−4$, que contiene punto$(−3,−5)$

77. Conteniendo los puntos$(−3,−4)$ y$(2,−5)$

Responder: $y=−\frac{1}{5}x−\frac{23}{5}$

78. Conteniendo los puntos$(−5,−3)$ y$(4,−6)$

79. perpendicular a la línea$x−2y=5$, punto$(−2,2)$

Responder: $y=−2x−2$

80. perpendicular a la línea$4x+3y=1$, punto$(0,0)$

Ejercicios de escritura

81. ¿Por qué todas las líneas horizontales son paralelas?

Responder: Las respuestas variarán.

82. Explica con tus propias palabras por qué las pendientes de dos líneas perpendiculares deben tener signos opuestos.

Autocomprobación

a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

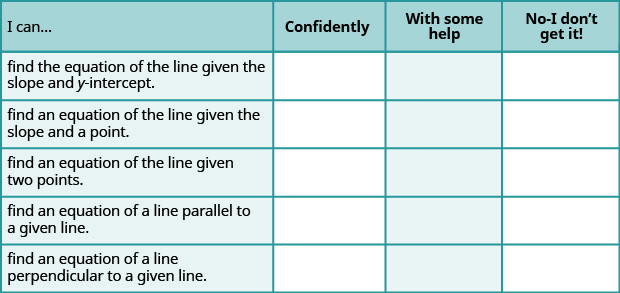
$La figura muestra una tabla con seis filas y cuatro columnas. La primera fila es una fila de encabezado y etiqueta cada columna. El encabezado de la primera columna es “puedo...”, el segundo es “con confianza”, el tercero es “con algo de ayuda”, “¡no menos no lo consigo!”. Debajo de la primera columna están las frases “encontrar la ecuación de la línea dada la pendiente e interceptar y”, “encontrar una ecuación de la línea dada la pendiente y un punto”, “encontrar una ecuación de la línea dada dos puntos”, “encontrar una ecuación de una línea paralela a una línea dada”, y “encontrar una ecuación de una línea perpendicular a una línea dada”. Debajo de la segunda, tercera, cuarta columnas son espacios en blanco donde el alumno puede verificar qué nivel de dominio ha logrado.$

b. ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?

Search

Text Color

Text Size

Margin Size

Font Type