3.6: Relaciones y Funciones

Última actualización
Guardar como PDF

Page ID: 112317

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Al final de esta sección, podrás:

Encuentra el dominio y el rango de una relación
Determinar si una relación es una función
Encontrar el valor de una función

Antes de comenzar, toma este cuestionario de preparación.

Evaluar$3x−5$ cuándo$x=−2$.
Si te perdiste este problema, revisa [enlace].
Evaluar$2x^2−x−3$ cuándo$x=a$.
Si te perdiste este problema, revisa [enlace].
Simplificar:$7x−1−4x+5$.
Si te perdiste este problema, revisa [enlace].

Encontrar el dominio y el rango de una relación

A medida que avanzamos en nuestra vida diaria, tenemos muchos elementos de datos o cantidades que se emparejan con nuestros nombres. Nuestro número de seguro social, número de identificación de estudiante, dirección de correo electrónico, número de teléfono y nuestro cumpleaños coinciden con nuestro nombre. Existe una relación entre nuestro nombre y cada uno de esos ítems.

Cuando tu profesor obtiene su lista de clases, los nombres de todos los estudiantes de la clase se enumeran en una columna y luego es probable que el número de identificación del estudiante esté en la siguiente columna. Si pensamos en la correspondencia como un conjunto de pares ordenados, donde el primer elemento es un nombre de estudiante y el segundo elemento es el número de identificación de ese estudiante, llamamos a esto una relación.

\[(\text{Student name}, \text{ Student ID #})\nonumber \]

El conjunto de todos los nombres de los alumnos en la clase se llama el dominio de la relación y el conjunto de todos los números de identificación de estudiante emparejados con estos estudiantes es el rango de la relación.

Hay muchas situaciones similares en las que una variable se empareja o se empareja con otra. El conjunto de pares ordenados que registra esta coincidencia es una relación.

Definición: Relación

Una relación es cualquier conjunto de pares ordenados,$(x,y)$. Todos los valores x en los pares ordenados forman juntos el dominio. Todos los valores y de los pares ordenados forman juntos el rango.

Ejemplo$\PageIndex{1}$

Para la relación${(1,1),(2,4),(3,9),(4,16),(5,25)}$:

Encuentra el dominio de la relación.
Encuentra el rango de la relación.

Contestar: \[\begin{array} {ll} {} &{ {\{(1,1), (2,4), (3,9), (4,16), (5,25) }\} } \\ {ⓐ\text{ The domain is the set of all x-values of the relation.}} &{ {\{1,2,3,4,5}\} } \\ {ⓑ\text{ The range is the set of all y-values of the relation.}} &{ {\{1,4,9,16,25}\} } \\ \nonumber \end{array}\]

Ejemplo$\PageIndex{2}$

Para la relación${\{(1,1),(2,8),(3,27),(4,64),(5,125)}\}$:

Encuentra el dominio de la relación.
Encuentra el rango de la relación.

Contestar a: ${\{1,2,3,4,5}\}$
Respuesta b: ${\{1,8,27,64,125}\}$

Ejemplo$\PageIndex{3}$

Para la relación${\{(1,3),(2,6),(3,9),(4,12),(5,15)}\}$:

Encuentra el dominio de la relación.
Encuentra el rango de la relación.

Contestar a: ${\{1,2,3,4,5}\}$
Respuesta b: ${\{3,6,9,12,15}\}$

MAPEO

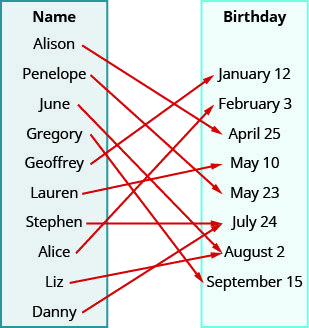
A veces se usa un mapeo para mostrar una relación. Las flechas muestran el emparejamiento de los elementos del dominio con los elementos del rango.

Ejemplo$\PageIndex{4}$

Utilice el mapeo de la relación que se muestra para

enumerar los pares ordenados de la relación,
encontrar el dominio de la relación, y
encontrar el rango de la relación.

$Esta figura muestra dos tablas que cada una tiene una columna. El cuadro de la izquierda tiene el encabezado “Nombre” y enumera los nombres “Alison”, “Penélope”, “June”, “Gregory”, “Geoffrey”, “Lauren”, “Stephen”, “Alice”, “Liz”, “Danny”. El cuadro de la derecha tiene el encabezado “Cumpleaños” y enumera las fechas “12 de enero”, “3 de febrero”, “25 de abril”, “10 de mayo”, “23 de mayo”, “24 de julio”, “2 de agosto” y “15 de septiembre”. Hay una flecha para cada nombre en la tabla Nombre que comienza en el nombre y apunta hacia una fecha en la tabla Cumpleaños. Si bien la mayoría de las fechas solo tienen una flecha apuntando a ellas, hay dos flechas que apuntan al 24 de julio: una de Stephen y otra de Liz.$

Contestar

ⓐ La flecha muestra la coincidencia de la persona con su cumpleaños. Creamos pares ordenados con el nombre de la persona como el valor x y su cumpleaños como el valor y.

{(Alison, 25 de abril), (Penélope, 23 de mayo), (junio, 2 de agosto), (Gregory, 15 de septiembre), (Geoffrey, 12 de enero), (Lauren, 10 de mayo), (Stephen, 24 de julio), (Alice, 3 de febrero), (Liz, 2 de agosto), (Danny, 24 de julio)}

ⓑ El dominio es el conjunto de todos los x -valores de la relación.

{Alison, Penélope, June, Gregory, Geoffrey, Lauren, Stephen, Alice, Liz, Danny}

{12 de enero, 3 de febrero, 25 de abril, 10 de mayo, 23 de mayo, 24 de julio, 2 de agosto, 15 de septiembre}

Ejemplo$\PageIndex{5}$

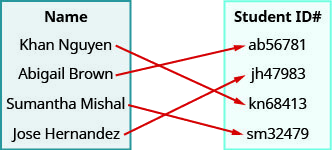
Utilice el mapeo de la relación que se muestra para

enumerar los pares ordenados de la relación
encontrar el dominio de la relación
encontrar el rango de la relación.

$Esta figura muestra dos tablas que cada una tiene una columna. El cuadro de la izquierda tiene el encabezado “Nombre” y enumera los nombres “Khanh Nguyen”, “Abigail Brown”, “Sumantha Mishal”, y “Jose Hern y ez”. La tabla de la derecha tiene el encabezado “Número de identificación de estudiante” y enumera los códigos “a b 56781”, “j h 47983”, “k n 68413”, y “s m 32479”. Hay una flecha para cada nombre en la tabla Nombre que comienza en el nombre y apunta hacia un código en la tabla de identificación de estudiante. La primera flecha va de Khanh Nguyen a k n 68413. La segunda flecha va de Abigail Brown a una b 56781. La tercera flecha va de Sumantha Mishal a s m 32479. La cuarta flecha va de Jose Hern y ez a j h 47983.$

Contestar

ⓐ (Khanh Nguyen, kn68413), (Abigail Brown, ab56781), (Sumantha Mishal, sm32479), (Jose Hern y ez, jh47983)

ⓑ {Khanh Nguyen, Abigail Brown, Sumantha Mishal, Jose Hern y ez}

Ejemplo$\PageIndex{6}$

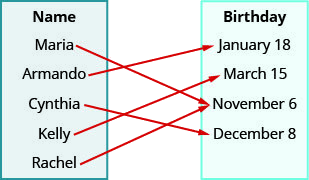
Utilice el mapeo de la relación que se muestra para

enumerar los pares ordenados de la relación
encontrar el dominio de la relación
encontrar el rango de la relación.

$Esta figura muestra dos tablas que cada una tiene una columna. La tabla de la izquierda tiene el encabezado “Nombre” y enumera los nombres “Maria”, “Arm and o”, “Cynthia”, “Kelly” y “Rachel”. El cuadro de la derecha tiene el encabezado “Cumpleaños” y enumera las fechas “18 de enero”, “15 de marzo”, “6 de noviembre” y “8 de diciembre”. Hay una flecha para cada nombre en la tabla Nombre que comienza en el nombre y apunta hacia una fecha en la tabla Cumpleaños. La primera flecha va de María al 6 de noviembre. La segunda flecha va de Brazo y o a un 18 de enero. La tercera flecha va de Cynthia al 8 de diciembre. La cuarta flecha va de Kelly al 15 de marzo. La quinta flecha va de Rachel al 6 de noviembre.$

Contestar

ⓐ (María, 6 de noviembre), (Arm y o, 18 de enero), (Cynthia, 8 de diciembre), (Kelly, 15 de marzo), (Rachel, 6 de noviembre)

ⓑ {María, Arm y o, Cynthia, Kelly, Rachel}

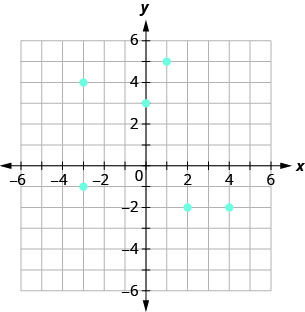
Una gráfica es otra forma más en la que se puede representar una relación. El conjunto de pares ordenados de todos los puntos trazados es la relación. El conjunto de todas las coordenadas x es el dominio de la relación y el conjunto de todas las coordenadas y es el rango. Generalmente escribimos los números en orden ascendente tanto para el dominio como para el rango.

Ejemplo$\PageIndex{7}$

Utilice la gráfica de la relación con

enumerar los pares ordenados de la relación
encontrar el dominio de la relación
encontrar el rango de la relación.

$La figura muestra la gráfica de algunos puntos en el plano de la coordenada x y. Los ejes x e y van de 6 a 6 negativos. Los puntos (negativo 3, 4), (negativo 3, negativo 1), (0, 3), (1, 5), (2, negativo 2), y (4, negativo 2).$

Contestar

ⓐ Los pares ordenados de la relación son:\[{\{(1,5),(−3,−1),(4,−2),(0,3),(2,−2),(−3,4)}\}.\nonumber\]

ⓑ El dominio es el conjunto de todos los x -valores de la relación:$\quad {\{−3,0,1,2,4}\}$.

Observe que mientras$−3$ se repite, solo se enumera una vez.

Observe que mientras$−2$ se repite, solo se enumera una vez.

Ejemplo$\PageIndex{8}$

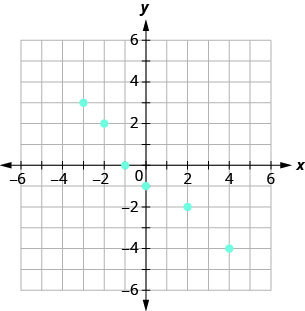
Utilice la gráfica de la relación con

enumerar los pares ordenados de la relación
encontrar el dominio de la relación
encontrar el rango de la relación.
$La figura muestra la gráfica de algunos puntos en el plano de la coordenada x y. Los ejes x e y van de 6 a 6 negativos. Los puntos (negativo 3, 3), (negativo 2, 2), (negativo 1, 0), (0, negativo 1), (2, negativo 2), y (4, negativo 4).$

Contestar: ⓐ$(−3,3),(−2,2),(−1,0),$
$(0,−1),(2,−2),(4,−4)$
ⓑ${\{−3,−2,−1,0,2,4}\}$
ⓒ${\{3,2,0,−1,−2,−4}\}$

Ejemplo$\PageIndex{9}$

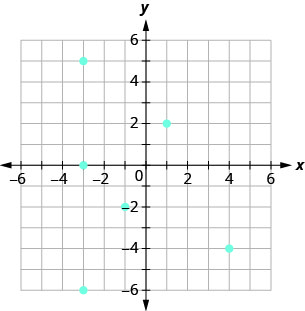
Utilice la gráfica de la relación con

enumerar los pares ordenados de la relación
encontrar el dominio de la relación
encontrar el rango de la relación.

$La figura muestra la gráfica de algunos puntos en el plano de la coordenada x y. Los ejes x e y van de 6 a 6 negativos. Los puntos (negativo 3, 5), (negativo 3, 0), (negativo 3, negativo 6), (negativo 1, negativo 2), (1, 2), y (4, negativo 4).$

Contestar: ⓐ$(−3,0),(−3,5),(−3,−6),$
$(−1,−2),(1,2),(4,−4)$
ⓑ${\{−3,−1,1,4}\}$
ⓒ${\{−6,0,5,−2,2,−4}\}$

Determinar si una relación es una función

Un tipo especial de relación, llamado función, ocurre extensamente en matemáticas. Una función es una relación que asigna a cada elemento en su dominio exactamente un elemento en el rango. Para cada par ordenado en la relación, cada valor x se hace coincidir con un solo valor y.

Definición: Función

Una función es una relación que asigna a cada elemento en su dominio exactamente un elemento en el rango.

El ejemplo de cumpleaños de Example nos ayuda a entender esta definición. Cada persona tiene un cumpleaños pero nadie tiene dos cumpleaños. Está bien que dos personas compartan un cumpleaños. ^{Está bien que Danny y Stephen compartan el 24 de julio como su cumpleaños y que June y Liz compartan el 2 de ^agosto.} Dado que cada persona tiene exactamente un cumpleaños, la relación en Ejemplo es una función.

La relación que muestra la gráfica en Ejemplo incluye los pares ordenados$(−3,−1)$ y$(−3,4)$. ¿Está bien en una función? No, ya que esto es como una persona teniendo dos cumpleaños diferentes.

Ejemplo$\PageIndex{10}$

Utilice el conjunto de pares ordenados para (i) determinar si la relación es una función (ii) encontrar el dominio de la relación (iii) encontrar el rango de la relación.

${\{(−3,27),(−2,8),(−1,1),(0,0),(1,1),(2,8),(3,27)}\}$
${\{(9,−3),(4,−2),(1,−1),(0,0),(1,1),(4,2),(9,3)}\}$

Contestar

ⓐ${\{(−3,27),(−2,8),(−1,1),(0,0),(1,1),(2,8),(3,27)}\}$

(i) Cada valor x se hace coincidir con un solo valor y. Entonces esta relación es una función.

(ii) El dominio es el conjunto de todos los valores x en la relación.
El dominio es:${\{−3,−2,−1,0,1,2,3}\}$.

(iii) El rango es el conjunto de todos los valores y en la relación. Observe que no enumeramos valores de rango dos veces.
El rango es:${\{27,8,1,0}\}$.

ⓑ${\{(9,−3),(4,−2),(1,−1),(0,0),(1,1),(4,2),(9,3)}\}$

(i) El valor x 9 se empareja con dos valores y, ambos 3 y$−3$. Entonces esta relación no es una función.

(ii) El dominio es el conjunto de todos los valores x en la relación. Observe que no enumeramos los valores de dominio dos veces.
El dominio es:${\{0,1,2,4,9}\}$.

(iii) El rango es el conjunto de todos los valores y en la relación.
El rango es:${\{−3,−2,−1,0,1,2,3}\}$.

Ejemplo$\PageIndex{11}$

Utilice el conjunto de pares ordenados para (i) determinar si la relación es una función (ii) encontrar el dominio de la relación (iii) encontrar el rango de la función.

${\{(−3,−6),(−2,−4),(−1,−2),(0,0),(1,2),(2,4),(3,6)}\}$
${\{(8,−4),(4,−2),(2,−1),(0,0),(2,1),(4,2),(8,4)}\}$

Contestar: ⓐ Sí;${\{−3,−2,−1,0,1,2,3}\}$;
${\{−6,−4,−2,0,2,4,6}\}$
ⓑ No;${\{0,2,4,8}\}$;
${\{−4,−2,−1,0,1,2,4}\}$

Ejemplo$\PageIndex{12}$

Utilice el conjunto de pares ordenados para (i) determinar si la relación es una función (ii) encontrar el dominio de la relación (iii) encontrar el rango de la relación.

${\{(27,−3),(8,−2),(1,−1),(0,0),(1,1),(8,2),(27,3)}\}$
${\{(7,−3),(−5,−4),(8,−0),(0,0),(−6,4),(−2,2),(−1,3)}\}$

Contestar: ⓐ No;${\{0,1,8,27}\}$;
${\{−3,−2,−1,0,2,2,3}\}$
ⓑ Sí;${\{7,−5,8,0,−6,−2,−1}\}$;
${\{−3,−4,0,4,2,3}\}$

Ejemplo$\PageIndex{13}$

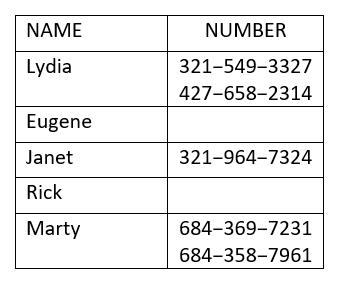
Utilice el mapeo para

determinar si la relación es una función
encontrar el dominio de la relación
encontrar el rango de la relación.

$clipboard_e358fef1793647353f09157074f4029e0.png$

Contestar

ⓐ Tanto Lydia como Marty tienen dos números de teléfono. Por lo tanto, cada valor x no coincide con un solo valor y. Entonces esta relación no es una función.

ⓑ El dominio es el conjunto de todos los valores x en la relación. El dominio es: {Lydia, Eugene, Janet, Rick, Marty}

${\{321-549-3327, 427-658-2314, 321-964-7324, 684-358-7961, 684-369-7231, 798-367-8541}\}$

Ejemplo$\PageIndex{14}$

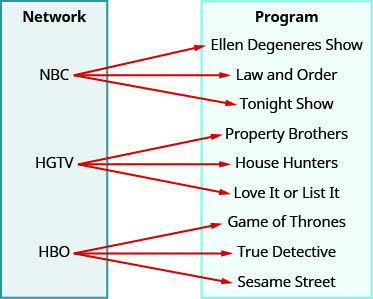
Utilice el mapeo para ⓐ determinar si la relación es una función ⓑ encontrar el dominio de la relación ⓒ encontrar el rango de la relación.

$Esta figura muestra dos tablas que cada una tiene una columna. La mesa de la izquierda tiene el encabezado “Red” y enumera las estaciones de televisión “NBC”, “HGTV”, y “HBO”. La mesa de la derecha tiene el encabezado “Programa” y enumera los programas de televisión “Ellen Degeneres Show”, “Ley y orden”, “Tonight Show”, “Property Brothers”, “House Hunters”, “Love it or List it”, “Game of Thrones”, “True Detective”, y “Barrio Sésamo”. Hay flechas que comienzan en una red en la primera tabla y apuntan hacia un programa en la segunda tabla. La primera flecha va de NBC a Ellen Degeneres Show. La segunda flecha va de NBC a Ley y Orden. La tercera flecha va de NBC a Tonight Show. La cuarta flecha va de HGTV a Property Brothers. La quinta flecha va de HGTV a House Hunters. La sexta flecha va de HGTV a Love it o List it. La séptima flecha va de HBO a Game of Thrones. La octava flecha va de HBO a True Detective. La novena flecha va de HBO a la Calle Sésamo.$

Contestar: ⓐ no ⓑ {NBC, HGTV, HBO} ⓒ {Show de Ellen Degeneres, Ley y orden, Tonight Show, Property Brothers, House Hunters, Love it or List it, Game of Thrones, True Detective, Barrio Sésamo}

Ejemplo$\PageIndex{15}$

Utilice el mapeo para

determinar si la relación es una función
encontrar el dominio de la relación
encontrar el rango de la relación.

Contestar: ⓐ No ⓑ {Neal, Krystal, Kelvin, George, Christa, Mike} ⓒ {123-567-4839 trabajo, 231-378-5941 celda, 743-469-9731 celda, 567-534-2970 trabajo, 684-369-7231 celda, 798-367-8541 celda, 639-847-6971 celda}

En álgebra, la mayoría de las veces, las funciones estarán representadas por una ecuación. Es más fácil ver si la ecuación es una función cuando se resuelve para y. Si cada valor de x da como resultado un solo valor de y, entonces la ecuación define una función.

Ejemplo$\PageIndex{16}$

Determinar si cada ecuación es una función.

$2x+y=7$
$y=x^2+1$
$x+y^2=3$

Contestar

ⓐ$2x+y=7$

Por cada valor de x, lo multiplicamos por$−2$ y luego sumamos 7 para obtener el valor y

	$.$
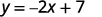
Por ejemplo, si$x=3$:	$.$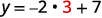
	$.$

Tenemos eso cuando$x=3$, entonces$y=1$. Funcionaría de manera similar para cualquier valor de x. Dado que cada valor de x, corresponde a un solo valor de y la ecuación define una función.

ⓑ$y=x^2+1$

Por cada valor de x, lo cuadramos y luego agregamos 1 para obtener el valor y.

	$.$
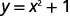
Por ejemplo, si$x=2$:	$.$
	$.$

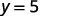
Tenemos eso cuando$x=2$, entonces$y=5$. Funcionaría de manera similar para cualquier valor de x. Dado que cada valor de x, corresponde a un solo valor de y la ecuación define una función.

ⓒ

	$.$
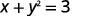
Aislar el término y.	$.$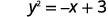
Vamos a sustituir$x=2$.	$.$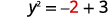
	$.$
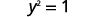
Esto nos da dos valores para y.	$y=1\space y=−1$

Nosotros hemos demostrado que cuando$x=2$, entonces$y=1$ y$y=−1$. Funcionaría de manera similar para cualquier valor de x. Dado que cada valor de x no corresponde a un solo valor de y la ecuación no define una función.

Ejemplo$\PageIndex{17}$

Determinar si cada ecuación es una función.

$4x+y=−3$
$x+y^2=1$
$y−x^2=2$

Contestar: ⓐ si ⓑ no ⓒ si

Ejemplo$\PageIndex{18}$

Determinar si cada ecuación es una función.

$x+y^2=4$
$y=x^2−7$
$y=5x−4$

Contestar: ⓐ no ⓑ si ⓒ si

Encontrar el valor de una función

Es muy conveniente nombrar una función y la mayoría de las veces la llamamos f, g, h, F, G o H. En cualquier función, por cada valor x del dominio obtenemos un valor y correspondiente en el rango. Para la función$f$, escribimos este valor de rango$y$ como$f(x)$. Esto se llama notación$f$ de función y se lee$x$ o el valor de$f$ at$x$. En este caso los paréntesis no indican multiplicación.

Definición: Notación de funciones

Para la función$y=f(x)$

\[\begin{array} {l} {f\text{ is the name of the function}} \\{x \text{ is the domain value}} \\ {f(x) \text{ is the range value } y \text{ corresponding to the value } x} \\ \nonumber \end{array}\]

Leemos$f(x)$ como$f$ de$x$ o el valor de$f$ at$x$.

Llamamos a x la variable independiente ya que puede ser cualquier valor en el dominio. Llamamos a y la variable dependiente ya que su valor depende de x.

Variables independientes y dependientes

Para la función$y=f(x)$,

\[\begin{array} {l} {x \text{ is the independent variable as it can be any value in the domain}} \\ {y \text{ the dependent variable as its value depends on } x} \\ \nonumber \end{array}\]

Al igual que cuando se encontró por primera vez con la variable x, la notación de funciones puede ser bastante inquietante. Parece extraño porque es nuevo. Te sentirás más cómodo con la notación a medida que la uses.

Veamos la ecuación$y=4x−5$. Para encontrar el valor de y cuando$x=2$, sabemos sustituir$x=2$ en la ecuación y luego simplificar.

	$.$
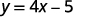Dejar x=2.	$.$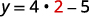
	$.$

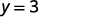El valor de la función at$x=2$ es 3.

Hacemos lo mismo usando la notación de funciones, la ecuación se$y=4x−5$ puede escribir como$f(x)=4x−5$. Para encontrar el valor cuando$x=2$, escribimos:

	$.$
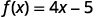Dejar x=2.	$.$
	$.$

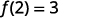El valor de la función at$x=2$ es 3.

Este proceso de encontrar el valor de$f(x)$ para un valor dado de x se llama evaluar la función.

Ejemplo$\PageIndex{19}$

Para la función$f(x)=2x^2+3x−1$, evalúe la función.

$f(3)$
$f(−2)$
$f(a)$

Contestar

ⓐ

	$.$
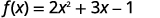
Para evaluar$f(3)$, sustituya 3 por x.	$.$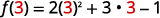
Simplificar.	$.$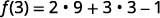
	$.$
	$.$

ⓑ

		$.$
$.$		$.$
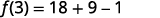
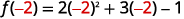
Simplificar.		$.$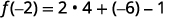
		$.$
		$.$

ⓒ

	$.$
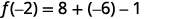
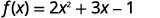
Para evaluar f (a), f (a), sustituir a por x.	$.$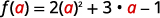
Simplificar.	$.$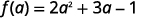

Ejemplo$\PageIndex{20}$

Para la función$f(x)=3x^2−2x+1$, evalúe la función.

$f(3)$
$f(−1)$
$f(t)$

Ejemplo$\PageIndex{21}$

Para la función$f(x)=2x^2+4x−3$, evalúe la función.

$f(2)$
$f(−3)$
$f(h)$

En el último ejemplo, encontramos$f(x)$ para un valor constante de x. En el siguiente ejemplo, se nos pide encontrar$g(x)$ con valores de x que sean variables. Seguimos el mismo procedimiento y sustituimos las variables por la x.

Ejemplo$\PageIndex{22}$

Para la función$g(x)=3x−5$, evalúe la función.

$g(h^2)$
$g(x+2)$
$g(x)+g(2)$

Contestar

ⓐ

			$.$
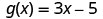
Para evaluar$g(h^2)$, sustituya$h^2$ por x.			$.$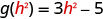
			$.$

ⓑ

	$.$
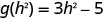
Para evaluar$g(x+2)$, sustituya$x+2$ por x.	$.$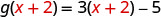
Simplificar.	$.$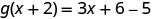
	$.$

ⓒ

		$.$
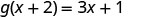
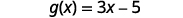
Para evaluar$g(x)+g(2)$, primero encuentra$g(2)$.		$.$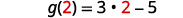
		$.$
$.$		$.$
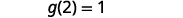
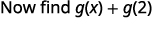
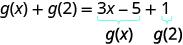
Simplificar.		$.$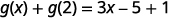
		$.$

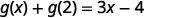
Observe la diferencia entre la parte ⓑ y ⓒ. Obtenemos$g(x+2)=3x+1$ y$g(x)+g(2)=3x−4$. Entonces vemos eso$g(x+2)\neq g(x)+g(2)$.

Ejemplo$\PageIndex{23}$

Para la función$g(x)=4x−7$, evalúe la función.

$g(m^2)$
$g(x−3)$
$g(x)−g(3)$

Ejemplo$\PageIndex{24}$

Para la función$h(x)=2x+1$, evalúe la función.

$h(k^2)$
$h(x+1)$
$h(x)+h(1)$

Muchas situaciones cotidianas se pueden modelar usando funciones.

Ejemplo$\PageIndex{25}$

El número de correos no leídos en la cuenta de Sylvia es 75. Este número crece en 10 correos electrónicos no leídos al día. La función$N(t)=75+10t$ representa la relación entre el número de correos electrónicos, N, y el tiempo, t, medido en días.

Determinar la variable independiente y dependiente.
Encuentra$N(5)$. Explique qué significa este resultado.

Contestar

ⓐ El número de correos electrónicos no leídos es una función del número de días. El número de correos no leídos, N, depende del número de días, t. Por lo tanto, la variable N, es la variable dependiente y la variable tt es la variable independiente.

ⓑ Encontrar$N(5)$. Explique qué significa este resultado.

	$.$
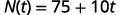
Sustituto en t=5.t=5.	$.$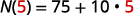
Simplificar.	$.$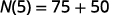
	$.$

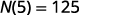
Ya que 5 es el número de días,$N(5)$, es el número de correos no leídos después de 5 días. Después de 5 días, hay 125 correos no leídos en la cuenta.

Ejemplo$\PageIndex{26}$

El número de correos electrónicos no leídos en la cuenta de Bryan es de 100. Este número crece en 15 correos electrónicos no leídos al día. La función$N(t)=100+15t$ representa la relación entre el número de correos electrónicos, N, y el tiempo, t, medido en días.

Determinar la variable independiente y dependiente.
Encuentra$N(7)]$. Explique qué significa este resultado.

Contestar: ⓐ t IND; N DEP ⓑ 205; el número de correos no leídos en la cuenta de Bryan al séptimo día.

Ejemplo$\PageIndex{27}$

El número de correos no leídos en la cuenta de Anthony es 110. Este número crece en 25 correos electrónicos no leídos al día. La función$N(t)=110+25t$ representa la relación entre el número de correos electrónicos, N, y el tiempo, t, medido en días.

Determinar la variable independiente y dependiente.
Encuentra$N(14)$. Explique qué significa este resultado.

Contestar: ⓐ t IND; N DEP ⓑ 460; el número de correos no leídos en la cuenta de Anthony al decimocuarto día

Acceda a este recurso en línea para obtener instrucción adicional y práctica con relaciones y funciones.

Introducción a las funciones

Conceptos clave

Notación de funciones: Para la función$y=f(x)$
- f es el nombre de la función
- x es el valor del dominio
- $f(x)$es el valor de rango y correspondiente al valor x
  Leemos$f(x)$ como f de x o el valor de f en x.
Variables Independientes y Dependientes: Para la función$y=f(x)$,
- x es la variable independiente ya que puede ser cualquier valor en el dominio
- y es la variable dependiente ya que su valor depende de x

Glosario

dominio de una relación: El dominio de una relación son todos los valores x en los pares ordenados de la relación.

función: Una función es una relación que asigna a cada elemento en su dominio exactamente un elemento en el rango.

mapeo: A veces se usa un mapeo para mostrar una relación. Las flechas muestran el emparejamiento de los elementos del dominio con los elementos del rango.

rango de una relación: El rango de una relación es todos los valores y- en los pares ordenados de la relación.

relación: Una relación es cualquier conjunto de pares ordenados, (x, y). (x, y). Todos los valores x en los pares ordenados forman juntos el dominio. Todos los valores y de los pares ordenados forman juntos el rango.

Search

Text Color

Text Size

Margin Size

Font Type

Definición: Relación

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\)

MAPEO

Ejemplo\(\PageIndex{4}\)

Ejemplo\(\PageIndex{5}\)

Ejemplo\(\PageIndex{6}\)

Ejemplo\(\PageIndex{7}\)

Ejemplo\(\PageIndex{8}\)

Ejemplo\(\PageIndex{9}\)

Definición: Función

Ejemplo\(\PageIndex{10}\)

Ejemplo\(\PageIndex{11}\)

Ejemplo\(\PageIndex{12}\)

Ejemplo\(\PageIndex{13}\)

Ejemplo\(\PageIndex{14}\)

Ejemplo\(\PageIndex{15}\)

Ejemplo\(\PageIndex{16}\)

Ejemplo\(\PageIndex{17}\)

Ejemplo\(\PageIndex{18}\)

Definición: Notación de funciones

Variables independientes y dependientes

Ejemplo\(\PageIndex{19}\)

Ejemplo\(\PageIndex{20}\)

Ejemplo\(\PageIndex{21}\)

Ejemplo\(\PageIndex{22}\)

Ejemplo\(\PageIndex{23}\)

Ejemplo\(\PageIndex{24}\)

Ejemplo\(\PageIndex{25}\)

Ejemplo\(\PageIndex{26}\)

Ejemplo\(\PageIndex{27}\)

	$.$
Aislar el término y.	$.$
Vamos a sustituir\(x=2\).	$.$
	$.$
Esto nos da dos valores para y.	\(y=1\space y=−1\)

	$.$
Para evaluar\(f(3)\), sustituya 3 por x.	$.$
Simplificar.	$.$
	$.$
	$.$

	$.$
Para evaluar\(g(x+2)\), sustituya\(x+2\) por x.	$.$
Simplificar.	$.$
	$.$

		$.$
Para evaluar\(g(x)+g(2)\), primero encuentra\(g(2)\).		$.$
		$.$
$.$		$.$
Simplificar.		$.$
		$.$